島式上層建筑總強度計算方法

于 濱，陳志堅，唐宇航

(海軍工程大學 艦船工程系，湖北 武漢 430033)

0 引 言

相比于航母寬闊的飛行甲板，航母上層建筑就像處于海洋中的島嶼，故稱之為島式上層建筑。島式上層建筑均采用偏離主船體中心線的方式設置，一般總長度跨主船體4～5 個站距，大致相當于一艘小型護衛艦的總長度，因而島式上層建筑存在總強度問題，且是航母工程中一個重要的局部強度問題。

對于島式上層建筑總強度，文獻[1]推薦采用有限條法：按上層建筑長度取一段含上層建筑的船體結構，取該長度為有限條的長度，將縱向加強筋平攤在外板、側壁板和縱向艙壁上，視船體（含上層建筑）橫截面為沿縱向無變化的單一幾何圖形而進行有限條的橫向劃分，在有限條的兩端作用總縱彎矩而求出各有限條的位移，在此基礎上求出上層建筑的應力而得到其總強度。這種方法較簡便，所需計算機內存小，計算工作量較小，在計算機硬件技術尚不發達且對上層建筑強度計算精度要求不高的前提下，是一種不錯的選擇。但島式上層建筑其內外部結構非常復雜且不規則，不僅整體不對稱且各層結構大小存在差異，因此將實船結構離散成有限條會導致強度計算結果出現較大的誤差。隨著科學技術的發展，使船體強度計算所受到的計算技術硬件約束得以解除，且船體結構設計過程中總有因結構優化要求需要較高的強度計算精度，因此有必要研究比有限條法更先進的上層建筑總強度計算方法。本文基于有限元理論、船體總強度理論提出一種新的島式上層建筑總強度計算方法，該方法良好適應當前船體總強度計算現狀，可有效利用船舶結構設計計算過程中的船體總強度計算結果，可克服有限條法的缺點、滿足結構優化設計的要求。

1 上層建筑總強度計算理論及載荷分析

上層建筑在外載荷的作用下，會產生強度問題[2-3]。研究上層建筑的受載、上層建筑結構應力計算方法（力學模型）及強度判別標準（許用應力），即為上層建筑強度理論[4]。上層建筑強度理論含有上層建筑結構局部強度和上層建筑結構總強度2 個部分。

在上層建筑總強度計算方面，文獻[5]提出由主船體對上層建筑側壁的作用導致上層建筑受載而出現總強度問題。在邊界條件已知的基礎上，運用彈性力學的方法進行理論推導，分別求取各部分的應力，可稱之為彈性力學法。該方法要求上層建筑側壁結構、上層建筑甲板結構等必須處理成簡單幾何圖形和板模型，這將與實際上層建筑結構形成極大的差異，從而使所得的計算結果只能是一個近似解，且近似的程度難以事先確定。

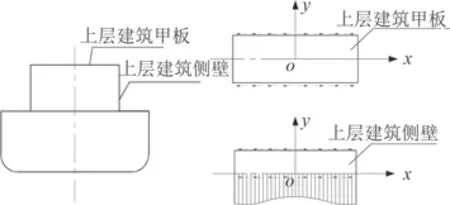
圖 1 計算上層建筑總強度的彈性力學模型Fig. 1 Elasticity model for calculating the total strength of superstructure

文獻[5]介紹了一種組合梁法。將整個船體分離成主船體和上層建筑兩部分，近似為兩根梁，兩者之間的相互作用用彈性支座來表示，運用彈性基礎梁的理論，并計入水平剪力的影響，依據變形協調條件建立彎曲微分方程組進行求解。

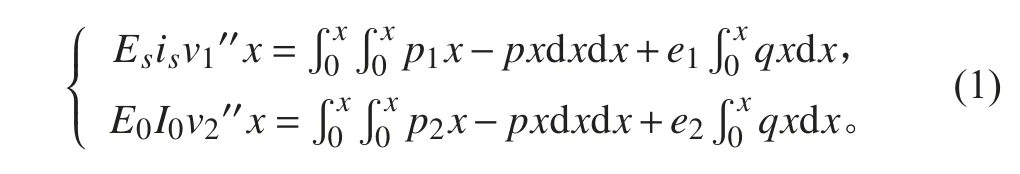
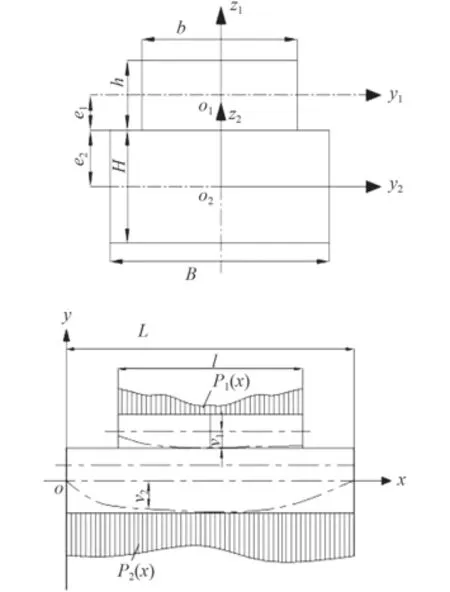
圖 2 計算上層建筑總強度的傳統組合梁法力學模型Fig. 2 The mechanical model of the traditional composite beam for calculating the total strength of the superstructure

Crawford[6]提出了改進的“雙梁理論”，即假定上層建筑和主船體都是單獨的梁，各自承受垂向力和水平力，主船體梁還承受外力矩，從而可以求得雙梁的正應力、撓度和曲率。相比于傳統的組合梁法，雙梁理論并未采用彈性基礎梁的微分方程，而是對垂向拉壓力與水平剪力作Fourier 變換，然后在若干假定的基礎上建立平衡方程求解，因此該方法更加簡單。

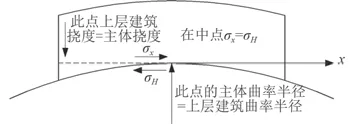
圖 3 計算上層建筑總強度的雙梁理論模型Fig. 3 Two-beam theoretical model for calculating the total strength of superstructure

文獻[7]介紹了計算上層建筑總強度的有限條法。如圖4 所示，將連續體割裂成部分連續部分離散的有限條，在條帶內假設位移函數如下式：

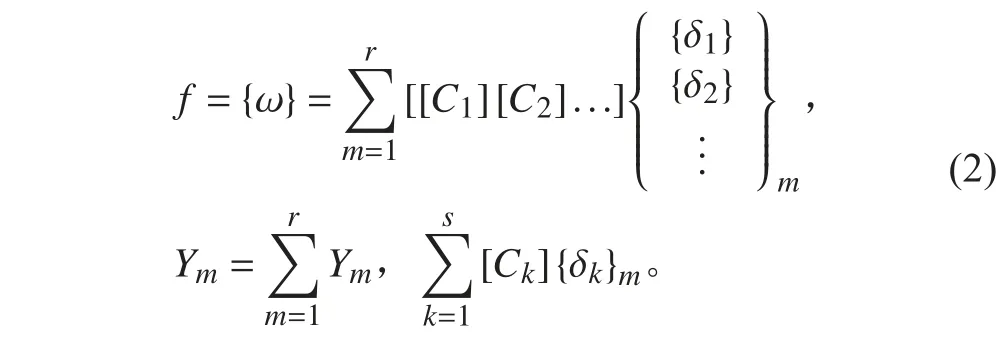
最終采用虛功原理或最小總勢能原理得到剛度矩陣和載荷矩陣，從而可以得到總剛度方程。顯然這種有限條法所逼近的結構只能是實際上層建筑結構的一個粗糙近似。

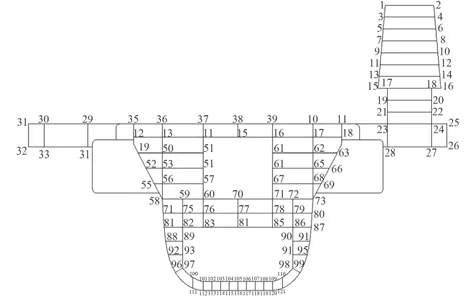
圖 4 主船體和上層建筑橫剖面節點示意面Fig. 4 Main hull and superstructure cross section node

從上述多種上層建筑總強度計算理論可以看出，上層建筑的載荷和強度判別標準基本不變，變化的主要是計算結構應力的力學計算模型。

2 基于有限元理論的島式上層建筑總強度計算

傳統的上層建筑總強度計算[8]的最大缺陷是所使用的結構力學模型過于簡單，與實船結構有較大的差異，從而導致計算結果精度較低，對于主船體加上層建筑形成的復雜彈性體結構來說，想要求解出精確解十分困難[9]。本文嘗試使用數值計算方法進行總強度的分析以克服上層建筑總強度傳統計算方法的缺陷。

2.1 力學模型及基本理論

目前使用最廣泛、最有效率的數值計算方法是有限元法[10]。有限元的基本思想是將一個連續物體離散為有限個單元，單元之間通過節點相連接，對每個單元根據位移函數和能量原理，推導出單元平衡方程，再將所有單元的平衡方程組集合在一起，得到結構總平衡方程。有限元法可克服上層建筑總強度傳統計算方法的缺陷，只要所取載荷精確，所得計算結果一定為問題的精確解。

對某船島式上層建筑結構，基于技術設計圖紙，在不對結構進行任何簡化的情況下，以板殼單元和梁單元離散上層建筑結構。板單元模擬上層建筑的甲板、側壁板、橫縱艙壁等板殼結構（構件），梁單元模擬骨材、桁材和桁架等，并考慮各構件的實際截面和偏心。建立上層建筑總強度有限元計算模型如圖5所示。

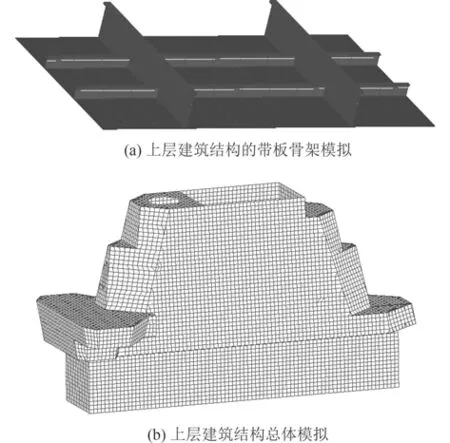
圖 5 計算上層建筑總強度的有限元模型Fig. 5 Finite element model for calculating the total strength of superstructures

2.2 總強度載荷及加載方法

上層建筑總強度載荷主要來源于主船體變形作用載荷。上層建筑結構與主船體連接在一起，主船體結構總縱彎矩作用下產生總縱彎曲撓度，該撓度產生時上層建筑亦將隨之變形從而產生總強度問題。

在船體總強度計算中，總是首先確定船體所受到的彎矩曲線。當艦船所受彎矩曲線已知，船體各截面相對于船體兩端的撓度值按下式計算：

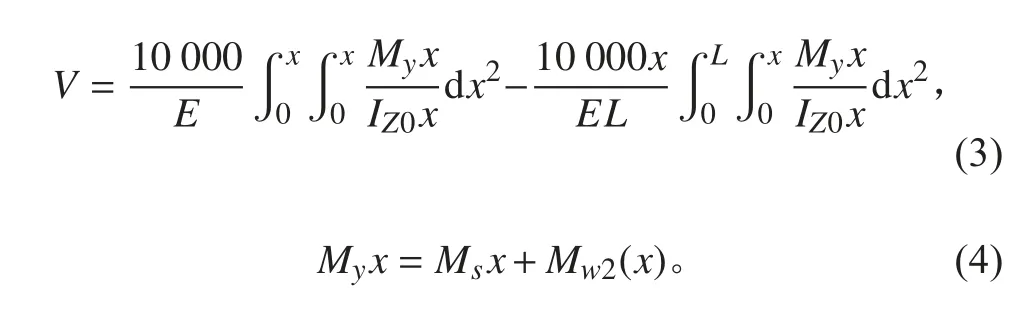
式中：V 為撓度值，m；L 為正常排水量時的艦船設計水線長，m；E 為彈性模量，MPa；為沿船長變化的彎矩分布，為沿船長變化的船體橫截面慣性矩分布，；為船體靜水彎矩沿船長的分布，kN·m；為船體波浪附加彎矩沿船長的分布，kN·m。

某船船體撓度曲線如圖6 所示。

截取船體撓度曲線中的上層建筑所在位置的值，以強迫位移邊界條件的形式引入有限元模型中，即可實現對上層建筑結構的加載。本文將某船的上層建筑部分，沿縱向劃分為13 站，利用所截取的撓度值插值求出前述13 站的絕對變形值和相對變形值如表1 所示，施加到模型相應位置。

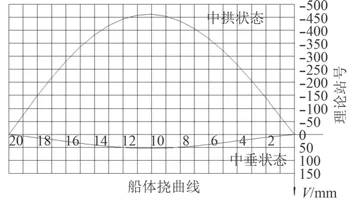
圖 6 中垂和中拱狀態下的船體撓曲線Fig. 6 In the middle and the arch state of the hull deflection curve

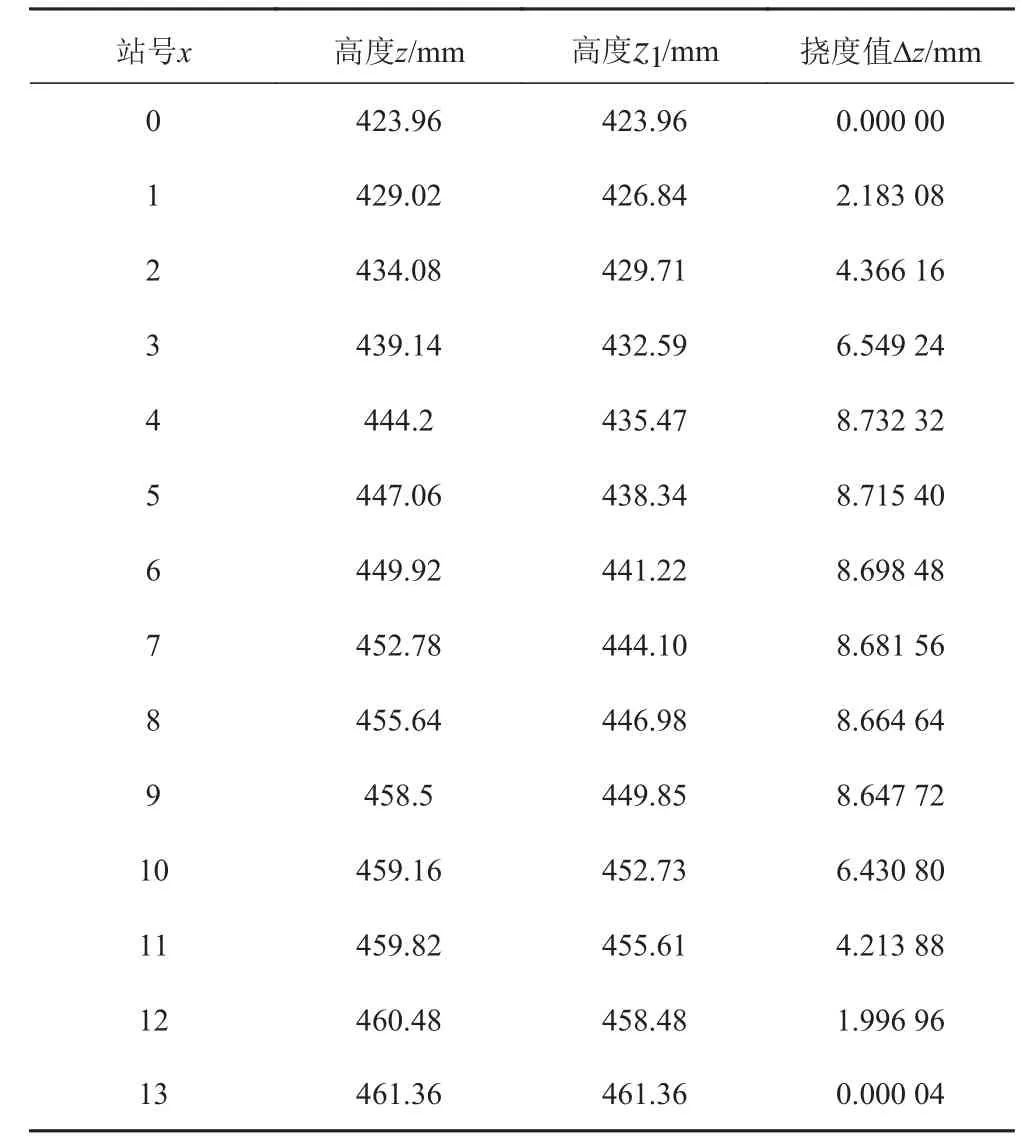
表 1 中拱狀態下上層建筑各站處的撓度值Tab. 1 The deflection value of each building in the superstructure in the arch state

2.3 計算結果及分析

分別使用有限元法和有限條法對某船上層建筑總強度進行計算。有限條法及計算模型如第1 節所述和圖4所示，有限元法及計算模型如第2.1 節所述及圖5 所示。有限條法與有限元法相應位置計算結果對比如圖7和圖8 所示。

對建立好的上層建筑有限元模型進行靜力分析，可以得到其總合正應力值，以及板、梁等局部結構的應力值。

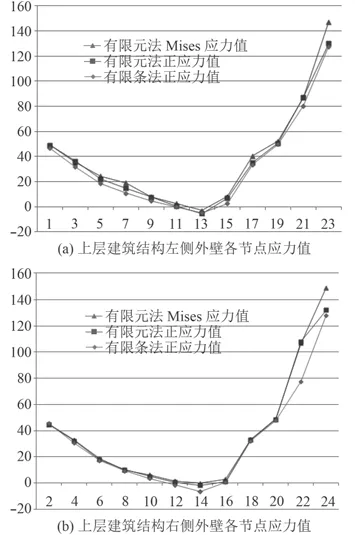
圖 7 上層建筑結構應力計算結果[注]Fig. 7 Calculation results of stress in superstructure

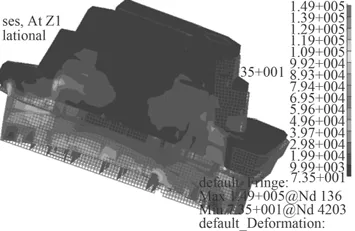
圖 8 上層建筑總強度有限元法計算結果Fig. 8 Finite element method for calculating the total strength of superstructure

有限條法計算結果表明，上層建筑總強度計算最大應力為128.1 MPa。有限元法計算結果表明，上層建筑總強度計算最大正應力和Mises 應力分別為132.1 MPa和149 MPa。

有限條法的“節點” 是代表實際結構的一條線，即“節線”。由有限條法理論和圖4 上層建筑有限條的離散圖可知，有限條法的計算結果會讓設計人員難以確定上層建筑結構最大應力的具體發生位置，如計算結果不符合要求需對結構進行改進設計時，顯然使用有限條法在結構改進設計上不方便。

由圖8 可以看出，最大應力發生點（圖中右側1.49+005 所對應標記）有明顯的應力集中特征。這說明有限元法可以發現上層建筑結構中最大應力的發生特征（即是否有應力集中現象），而有限條法做不到這一點。

3 結 語

本文首先認真分析了設計書中的有限條法計算過程，并提出將有限元法應用于計算上層建筑的強度。通過對比分析2 種方法的過程和結果，討論2 種方法的優劣及實用性，得出以下結論：

1）采用有限條法進行計算時，輸入和輸出數據少、矩陣階數少，在計算的簡便上有較大的優越性。而有限元法計算時，需要首先建立上層建筑的三維有限元模型，過程復雜，但是考慮到設計書中的校驗順序，在前期進行的船舶總強度計算中，已經建立起了整船有限元模型，可以十分方便地從中截取上層建筑部分，因此采用有限元法計算島式上層建筑的強度問題也有很好的實用性。

2）將本文的計算結果與有限條法的計算結果進行對比可以發現，有限條法計算出的應力值偏小，注意到有限條法對實際結構有較大的簡化，可以斷定誤差較大；有限元法填補了有限條法中只能縱向分條無法橫向離散的缺點，計算出的應力值更加真實。

3）有限條法是對整體結構的一種平均計算，無法細化到某個或者某些結構，而有限元法則彌補了這點不足，不僅能計算總合應力和局部結構的應力，還能計算結構中的集中應力，為結構強度預報提供依據。