插值濾波器的實現結構*

陳紹榮 ，劉郁林 ，何 為 ，徐 舜

（1.陸軍工程大學通信士官學校，重慶 400035；2.重慶市經信委，重慶 400015）

0 引 言

在國內外《數字信號處理》教材及著作[1-2]中，從不同角度介紹了實現抽樣頻率轉換的方法，歸納起來有3種實現抽樣頻率轉換的方法：（1）若原模擬信號xa(t)可以再生或是已經記錄下來，那么可以重新抽樣；（2）將x(n)通過D/A變換成模擬信號xa(t)后，對xa(t)經A/D再抽樣；（3）發展一套算法，對抽樣后的數字信號x(n)在“數字域”作抽樣率轉換，以得到新的抽樣。方法（1）有時不能實現，方法（2）要再一次受到D/A和A/D量化誤差的干擾，方法（3）是最理想的方法。減少抽樣率以去掉多余數據的過程稱為序列的重排；增加抽樣率以增加數據的過程，稱為序列的插值[3-4]。本文只討論有關插值濾波器的實現方法。

1 序列的插值

設周期為L的周期沖激序列為：

以均勻間隔T對連續時間信號xa(t)抽樣，得到序列x(n)=xa(nT)，若希望將抽樣率fs增加L倍，即變成Lfs，則最簡單的方法是對x(n)插值，用符號表示，即

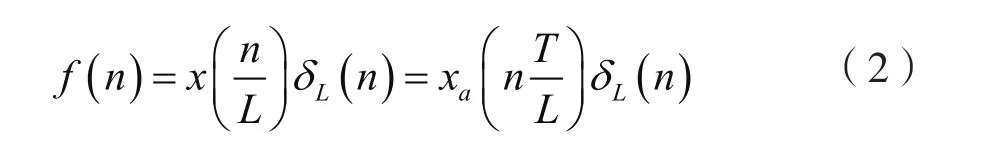
式（2）表明，對序列x(n)插值，等價于將連續時間信號xa(t)的抽樣間隔變成T/L，即抽樣率變成Lfs。

2 插值濾波器

考慮到式（1），對式（2）兩邊取DTFT，可得插值序列f(n)的頻譜，即：

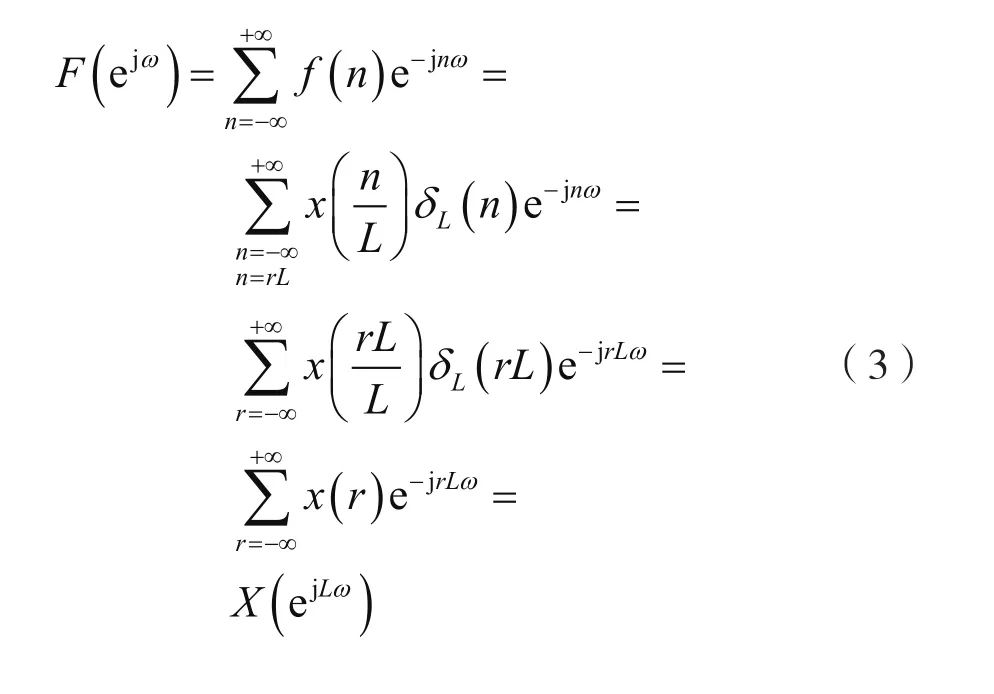
式（3）表明，插值序列f(n)的頻譜F(ejω)是序列x(n)的頻譜X(ejω)壓縮L倍的結果。換言之，在F(ejω)的主值區間 [-π,π]上，譜圖重復出現了L次，多余的L-1次稱為X(ejω)的映像。當|ω|≤π/L時，F(ejω)單一地等于X(ejLω)。可以利用后置數字低通濾波器來完成這一任務，如圖1所示，其中后置數字低通濾波器的頻率特性為：

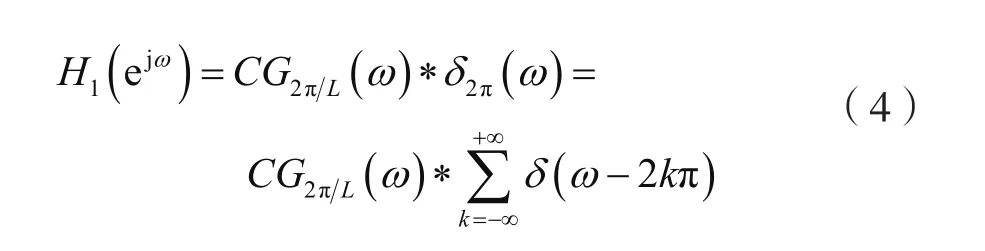
式中，C為常數，G2π/L(ω)=ε(ω+π/L)-ε(ω-π/L)，ε(ω)為單位階躍函數。

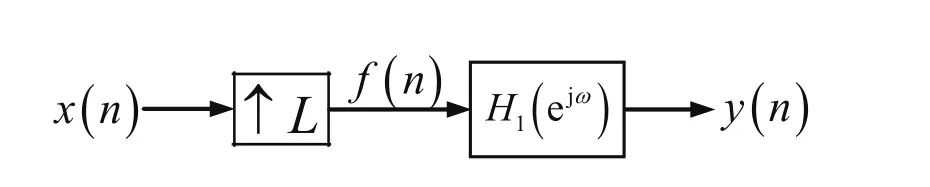
圖1 插值后的濾波

考慮到式（3）及式（4），則后置數字低通濾波器的輸出序列y(n)的頻譜為：

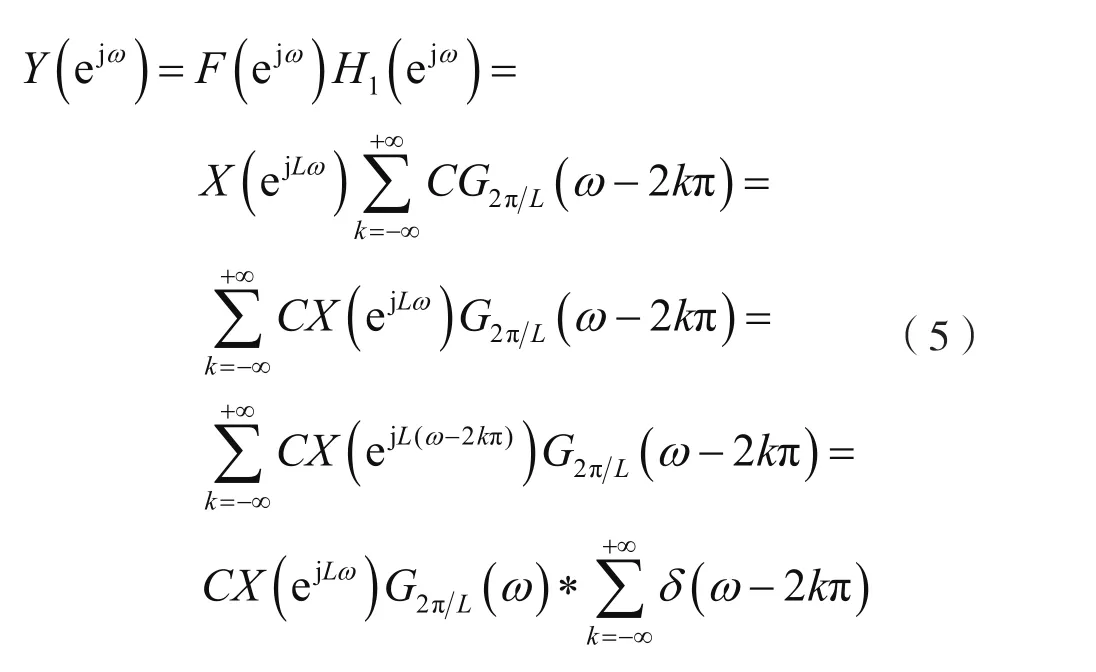
考慮到式（5），則有：

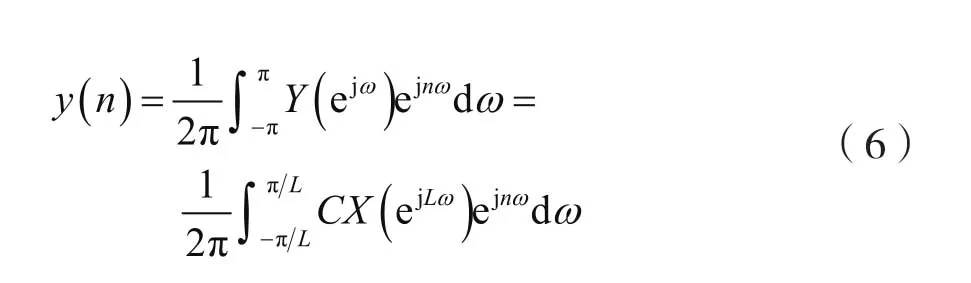
考慮到式（6），則有：

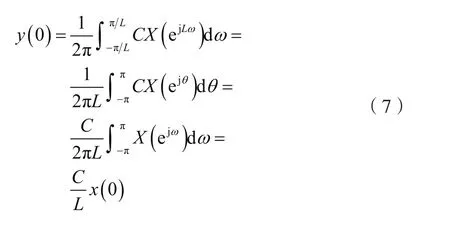
由式（7）可知，為保證y(0)=x(0)，則應取C=L，于是式（4）可寫成：

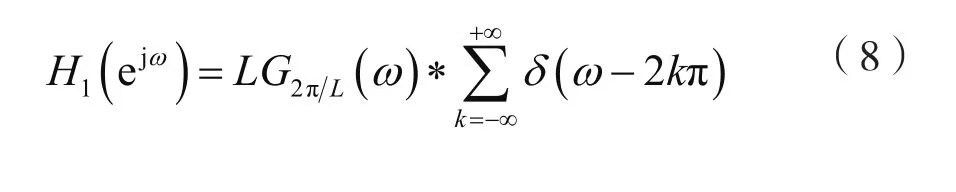
3 基于增抽樣的等價系統

基于增抽樣的系統Ⅰ，如圖2所示。

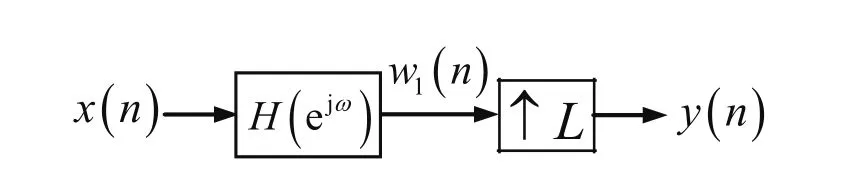
圖2 基于增抽樣的系統Ⅰ

在圖2中，有：

考慮到：

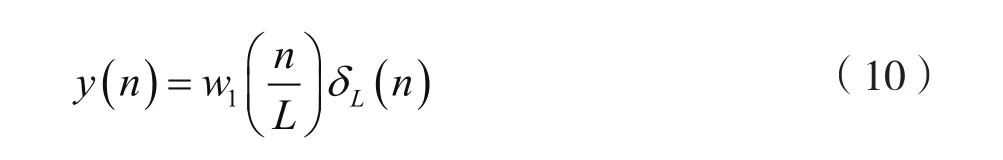
對式（10）兩邊取DTFT，并注意到式（3），則有：

將式（9）代入式（11），可得：

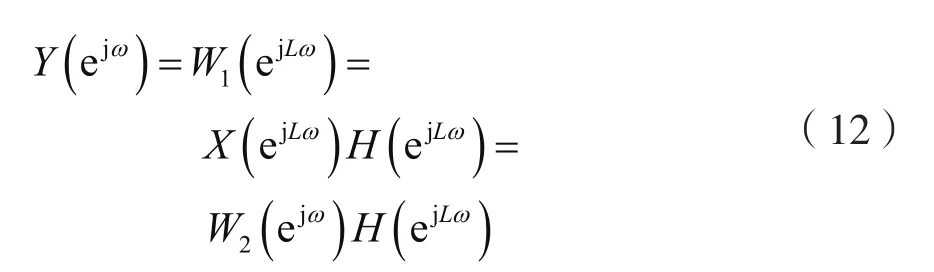
式中：

由式（12）及式（13），可得其等價系統，如圖3所示。

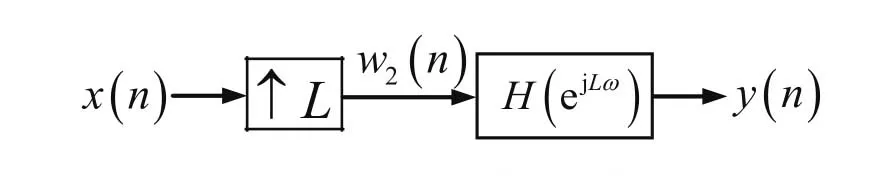
圖3 基于增抽樣的系統Ⅱ

結論1：對比圖3和圖2可知，若插值器從后置變為前置，則系統的頻率特性壓縮L倍；反之，若插值器從前置變為后置，則系統的頻率特性擴展L倍。這樣才能夠保證在相同輸入序列x(n)作用下，級聯系統有相同的輸出序列y(n)。

4 插值濾波器的實現結構

在如圖1所示的插值濾波中，數字低通濾波器H1(ejω)的單位沖激響應用h1(n)表示，一般都用FIR數字低通濾波器來實現該數字低通濾波器。設h1(n)的長度為N，即h1(n)=h1(n)RN(n)，并且滿足N/L為正整數。RN(n)=ε(n)-ε(n-N)，其中，ε(n)為單位階躍序列。

在實現如圖1所示的插值濾波時，存在下述5種具體實現結構。

4.1 插值濾波器的直接實現結構

考慮到圖1所示的插值濾波器，則有

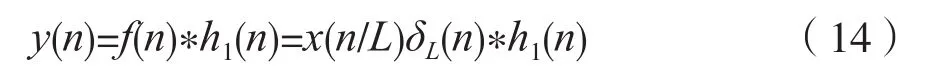
由式（14）可知，如圖1所示的插值濾波器，可以用如圖4所示的直接結構實現。

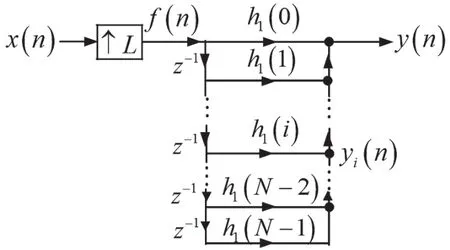
圖4 插值濾波器的直接實現

若對xa(t)以fs的速率抽樣獲得x(n)，則插值濾波器的直接實現結構有一個缺點，因為h1(n)工作在高抽樣率（即Lfs）狀態，插值序列f(n)的每一位的值都要和FIR數字低通濾波器h1(n)的系數相乘。由于插值序列f(n)中相距L位才有一位的值非零，因此，采用如圖4所示的直接實現結構，有較多的乘法浪費。

4.2 減少乘法次數的插值濾波器的直接實現結構

由于：

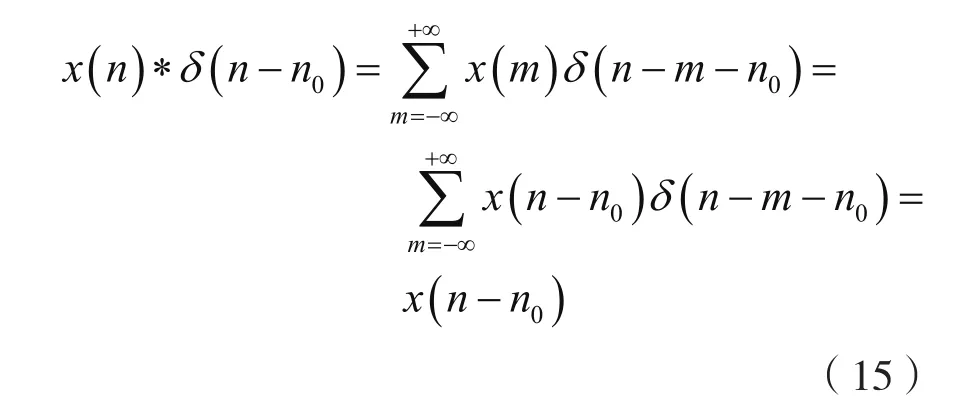
因此，從式（15）可知，一個序列與延遲n0位的單位沖激序列做線性卷和，等價于將該序列做n0位的延遲。

由圖4，結合式（2）及式（15），可得：

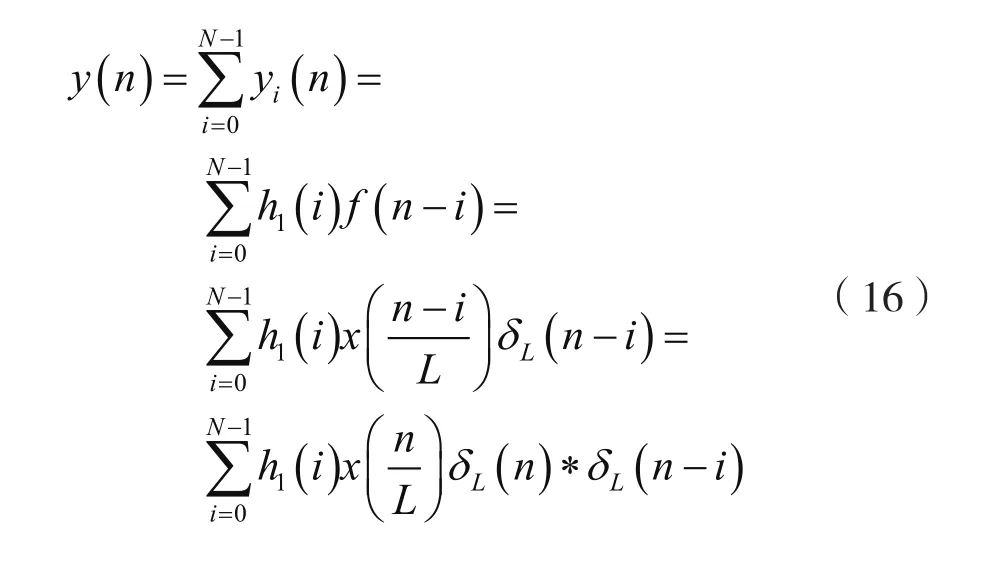
式（16）表明，先將輸入序列x(n)與h1(i)相乘，得到積序列再對積序列h1(i)x(n)做L點插值得到然后將延遲i位得到yi(n)，最后將yi(n)按式（16）相加得到輸出序列y(n)，如圖5所示。

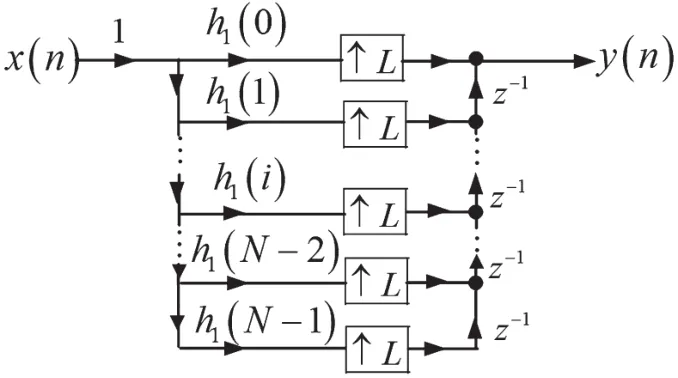
圖5 減少乘法次數的插值濾波器的直接實現結構

因此，與圖4所示的插值濾波器的直接實現結構相對照，更合理的方法是用圖5所示的結構來實現。在該圖中，先將輸入x(n)與h1(i)(i=0,1,…,N-1)相乘，然后再插值，所需要的乘法次數是圖4所示的插值濾波直接實現結構的1/L。

4.3 插值濾波器的分段實現結構

若定義L倍插值濾波器第j段的單位沖激響應為

式中，j=0,1,2,…,N/L-1，RL(n)=ε(n)-ε(n-L)。

由式（17）可知，利用pj(n)可以將FIR數字低通濾波器h1(n)分成N/L個子FIR數字濾波器，即式（16）可寫成：

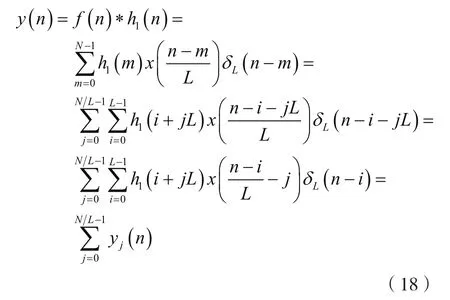
考慮到式（17），則式（18）中的yj(n)可以表示為：

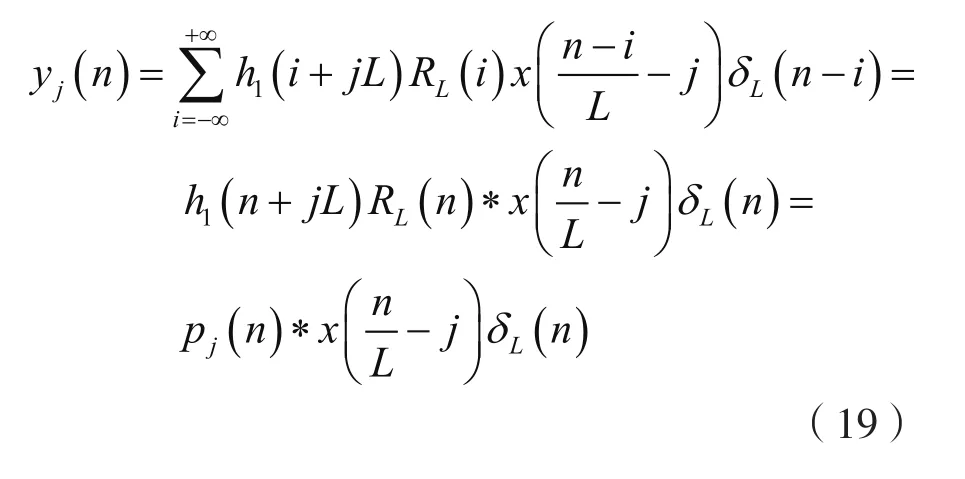
從式（18）及式（19）可知，可以將如圖1所示的插值濾波器中的FIR數字低通濾波器h1(n)分成N/L段，其中每一段是長度為L的子FIR數字濾波器，并且都具有相同結構。

若FIR數字低通濾波器h1(n)的長度N=9，取L=3，則三倍插值濾波器的分段實現結構，如圖6所示。

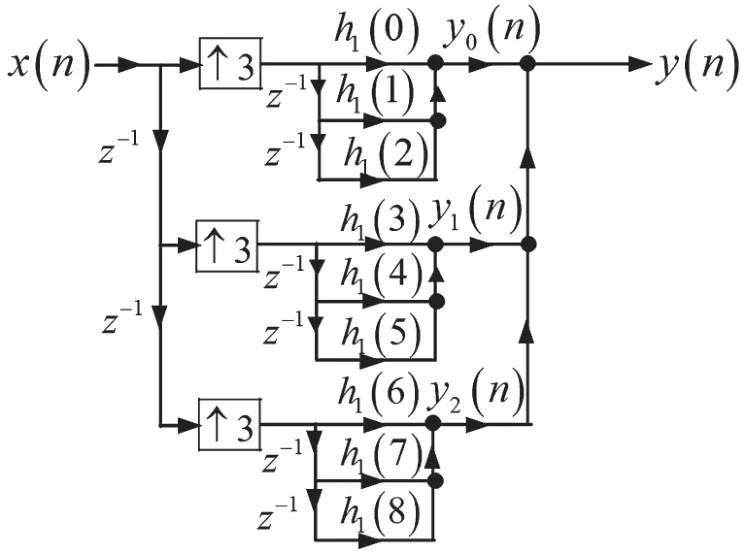
圖6 三倍插值濾波器的分段實現結構

4.4 減少單位延遲器的插值濾波器的分段實現結構

與插值濾波器的分段實現結構圖6相對照，更合理的方法是利用如圖7所示的結構來實現。在該實現結構中，單位延遲器的數目減少了一半。

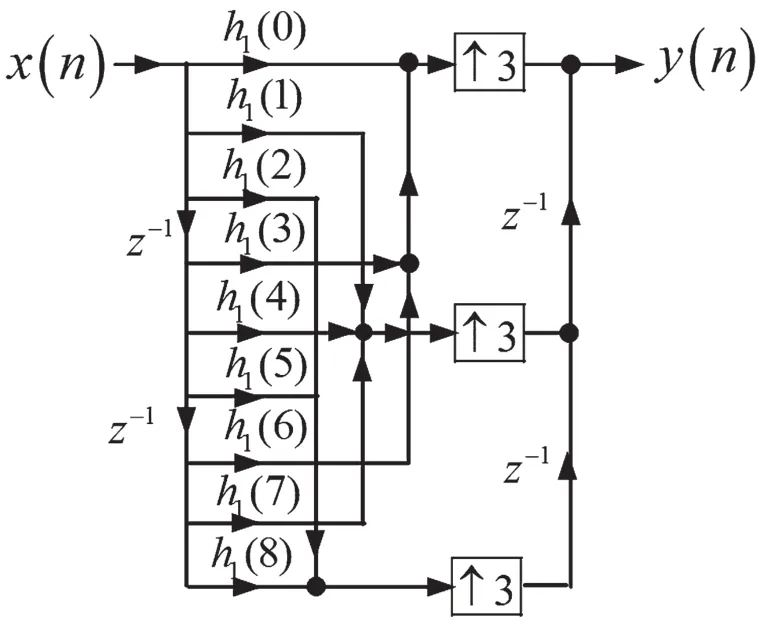
圖7 減少單位延遲器的三倍插值濾波器的分段實現結構

4.5 基于多相分解的插值濾波器的實現結構

從三倍插值濾波器的分段實現結構圖6可知，該實現結構對h1(n)的各段而言，其運算關系是先對輸入序列或其延遲序列插值，再進行濾波處理。因此，存在乘法運算的浪費，需要改善該實現結構。

由于：

考慮到式（14）及式（20），則有：

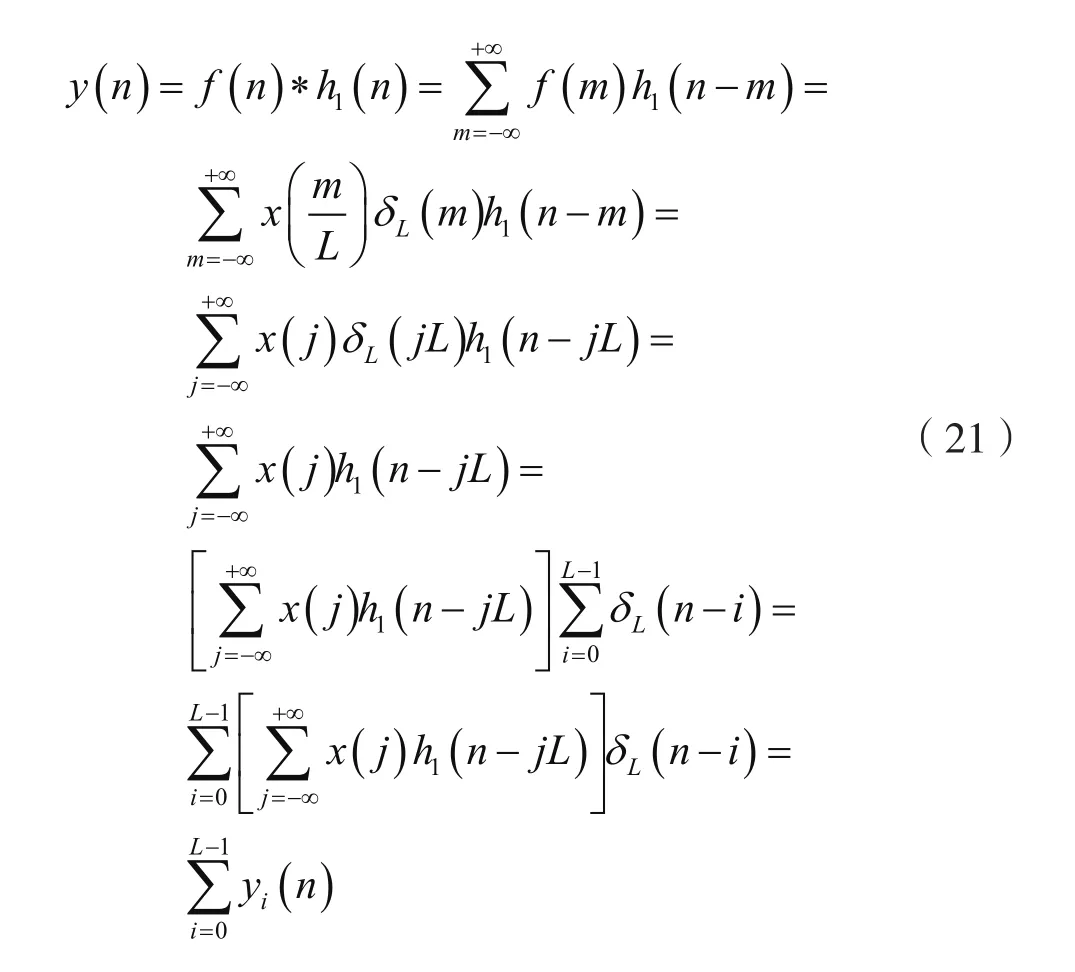
式中，yj(n)可以表示為：

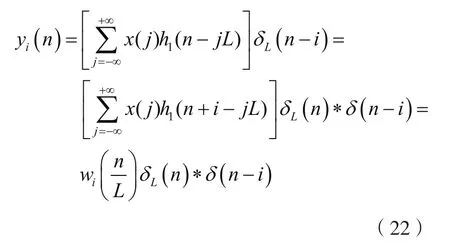
并且：

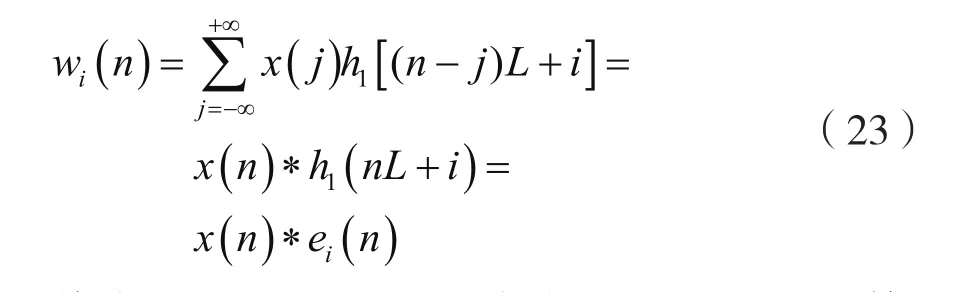
其中，ei(n)=h1(nL+i)，并稱ei(n)為h1(n)的第i個多相分量。

考慮到式（23）、式（22）及（21），則基于h1(n)多相分解的插值濾波器實現結構，如圖8所示。

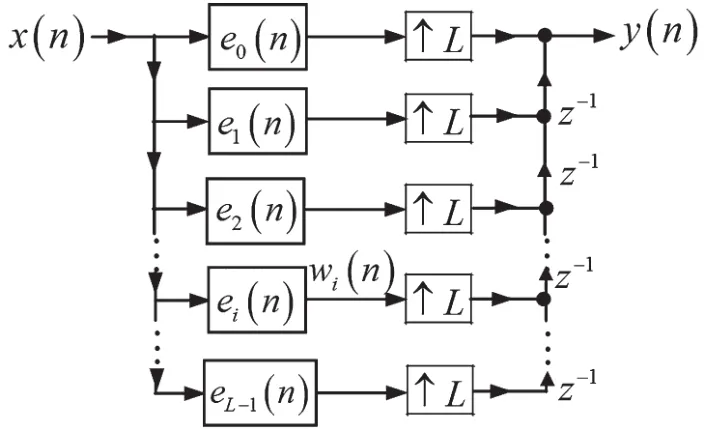
圖8 基于h1(n)多相分解的插值濾波器實現結構

若h1(n)是N=9點的FIR數字低通濾波器，取L=3，則將h1(n)分成了L=3個子FIR數字濾波器，各子FIR數字濾波器的長度為N/L=3，并且具有相同結構。考慮到式（21）、式（22）及（23），則基于h1(n)多相分解的插值濾波器實現結構，如圖9所示。

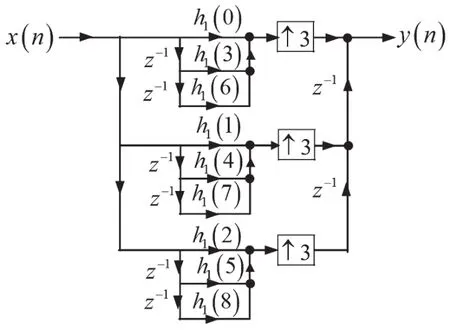
圖9 基于h1(n)多相分解的三倍插值濾波器實現結構

其實，可以通過下述方式獲得基于h1(n)多相分解的插值濾波器的實現結構。

設：

一般稱ei(n)為h1(n)的第i個多相分量。

令：

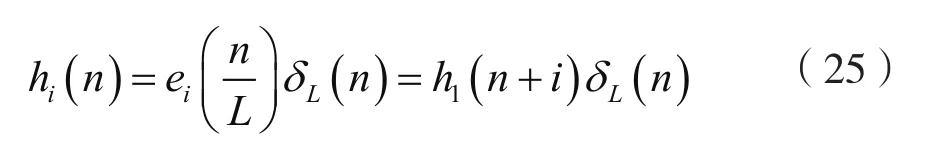
由式（25），結合式（20），可得：

式（26）表明，數字低通濾波器h1(n)可以分解成多相分量ei(n)=h1(nL+i)(i=0,1,2,…,L-1)的L倍插值hi(n)=(i=0,1,2,…,L-1)的延遲之和。

對式（25）兩邊取ZT，可得：

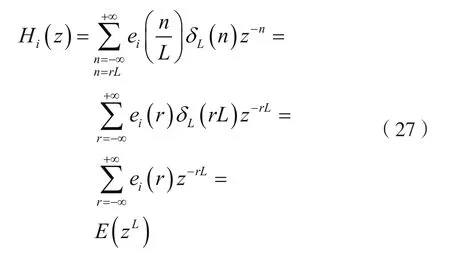
對式（26）兩邊取ZT，并注意到式（27），可得：

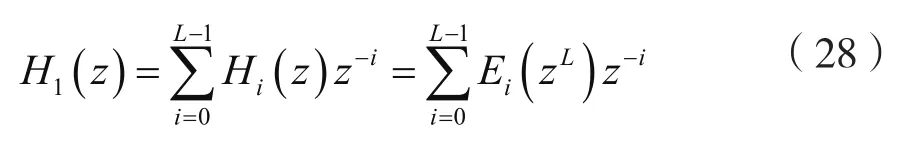
考慮到式（28），則可得基于數字低通濾波器h1(n)多相分解的實現結構，如圖10、圖11所示。

考慮到如圖11所示的基于數字低通濾波器h1(n)多相分解的實現結構，則如圖1所示的插值濾波器可用圖12來表示。

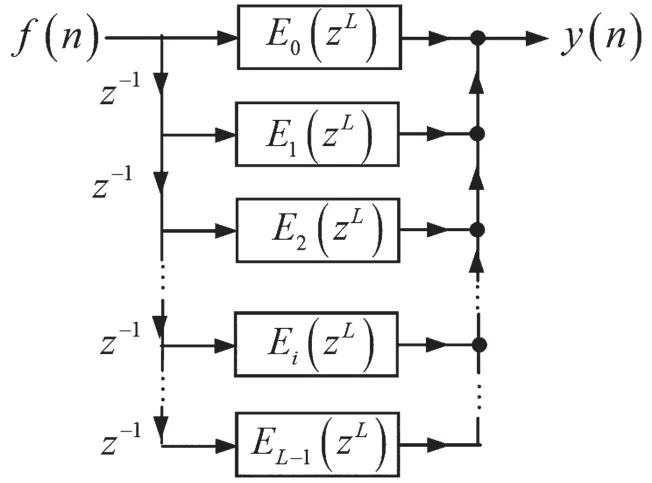
圖10 基于h1(n)多相分解的實現結構Ⅰ

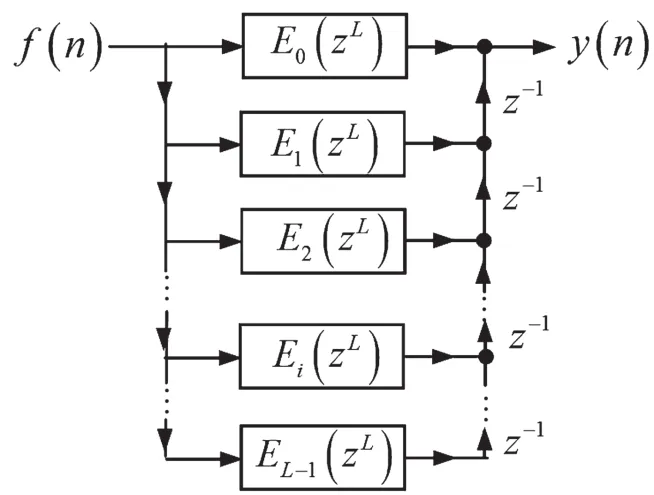
圖11 基于h1(n)多相分解的實現結構Ⅱ

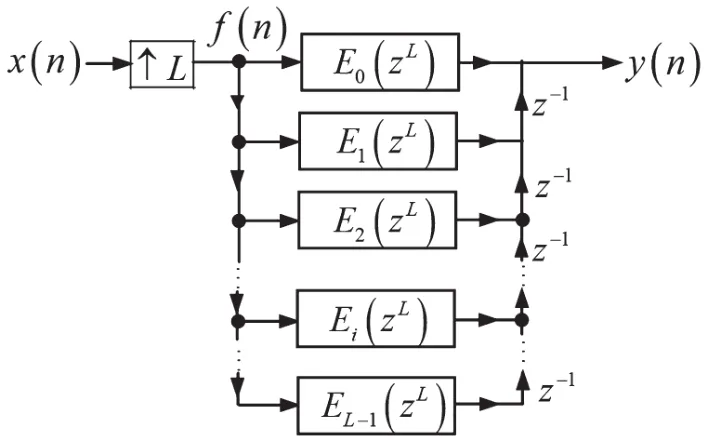
圖12 基于h1(n)多相分解的插值濾波器的實現結構Ⅰ

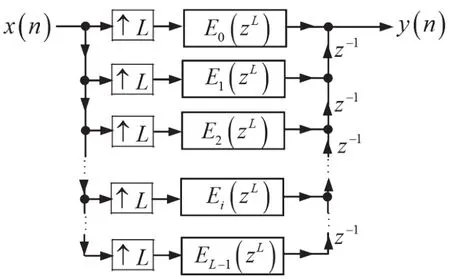
圖13 基于h1(n)多相分解的插值濾波器的實現結構Ⅱ

由于圖12中H1(z)的L個多相分解子數字濾波器的輸入序列f(n)是序列x(n)的L倍插值，因此可將圖12畫成圖13。

由結論1可知，將圖13中的插值器從前置變為后置，則子系統的頻率特性擴展L倍，即將子系統的轉移函數Ei(zL)(i=1,2,…,L-1)變成轉移函數Ei(z)(i=1,2,…,L-1)。這樣就得到了與圖8相同的基于數字低通濾波器h1(n)多相分解的插值濾波器的實現結構，如圖14所示，只不過其中的子系統用z域描述而已。

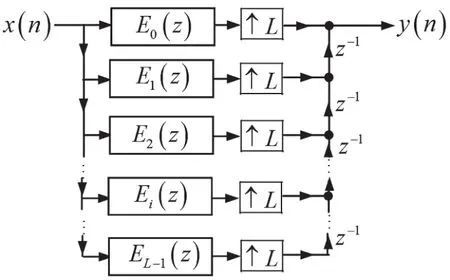
圖14 基于h1(n)多相分解的插值濾波器的實現結構Ⅲ

5 結 語

本文針對插值濾波器的實現問題，給出了插值濾波器的直接實現結構、減少乘法次數的插值濾波器的實現結構、插值濾波器的分段實現結構、減少單位延遲器的插值濾波器的分段實現結構及基于多相分解的插值濾波器的實現結構，并用一種新的思路和方法，導出了基于多相分解的插值濾波器的實現結構。