不要蘋果派,只要數學
衣魚

生日到了,媽媽端上一個蛋糕。你正想著要許一個什么愿望,媽媽開口說話了:“蛋糕是10寸的,也就是直徑約等于33厘米,那它的周長是多少?”你一臉尷尬,不情愿地說出了:“2πr,約等于103.62厘米。”媽媽繼續問:"那π是怎么來的?”你臉上頓時一個大寫的懵是阿基米德、劉徽、祖沖之算的……“媽,這是過生日,何必呢!
★阿基米德不吃蘋果派
阿基米德是一個為真理而活的人。他到底吃不吃蘋果派我不知道,但基本上可以說,美食于他而言只是為了活下去,除此之外沒啥用處。
普魯塔克在阿基米德的傳記里寫,阿基米德全力投入工作忘懷一切,要靠他的仆人將他從圖表旁邊拉開,才能在他身上涂抹油膏,幫他消除疲憊,甚至強制他去洗澡。這么一個號稱可以翹起地球的人,為了科學,可以說一點生活自理的能力都沒有。
在阿基米德時代,人們就發現不管多大、多小的圓,它的周長和直徑的比值是一個不變的常數。至于那個數字到底是多少,沒人知道。最后給它命了個名,叫π。
這個π到底是怎么得來的呢?很巧的是全世界的數學家都用了同一種算法,叫“割圓術”
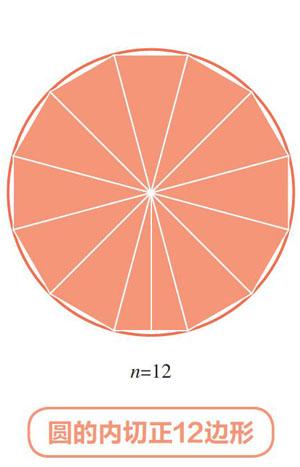
阿基米德發現,一個正多邊形,它的邊越多,它就越像圓。幾乎到正48邊形的時候,和圓就沒啥差別了。于是阿基米德在圓的里面和外面分別畫了2個相切的正多邊形,內切多邊形約束了圓周長的最小值,外切正多邊形約束了圓周長的最大值。
他從正6邊形開始算,直到正96邊形,得出3.140845<π<3.142857。小數點后第3位開始,差別變大就不可靠了。因此,阿基米德算出π約等于3.14,這個值也被我們沿用至今。
★世上無難事,只怕有心人
和阿基米德有點不一樣的是,中國數學家劉徽沒有用內切外切兩個多邊形來算,他用了更加簡潔的算法,只計算內切多邊形,算到了正96邊形時,他發現了一個更快捷的算法,只需要用正96邊形的數據,經過一次除法和一次加法,就可以得到正1536邊形的值。這個發現真是酷,他也因此得出一個他自己非常滿意的答案:π約等于3.1416。
三國時期,戰亂紛飛,劉徽一個人窩在家里搞學術,能算出這個答案,已經非常驚人了。
更厲害的地方在于,劉徽的快捷算法啟發了后來的數學家一祖沖之。是的,說到圓周率了,怎么能少得了他呢!祖沖之可以說是中國的圓周率之父。他在劉徽割圓術的基礎上計算了11次,得到了正12288邊形的周長,這個周長可以說是無限接近于圓。他得到的數字,π約等于3.1415926。祖沖之算出來的π,是接下來一千多年里最精確的圓周率。
執著于圓周率的數學家
17世紀前都用幾何方法(割圓術)算圓周率,德國數學家魯道夫花了大半輩子,把π算到了小數點后35位;后來微積分誕生,微積分和冪級數結合,產生了新的計算π的方法。1706年,英國數學家梅欽算到了小數點后100位。1874年英國的謝克斯用15年時間,把π算到了小數點后707位,這是人工計算π值的最高記錄,不過后來人們發現他從第528位開始就算錯了。
前不久的國際圓周率日(3月14日),谷歌工程師在計算機程序幫助下把π算到了31.4萬億位,人類的算法直接撲街,敗給了計算機。

