一種頻點裁剪算法在差分定位中的應用*

賴 川，高 科

（西南電子技術研究所，四川 成都 610036）

0 引 言

隨著美國全球定位系統（Global Positioning System，GPS）的建立，人們正式進入衛星導航時代。GPS系統早期是供美國軍方使用的，后期技術成熟后才逐步對民用開放。但是美國為了保障自己使用GPS的安全和利益，針對不同用戶，提供了標準定位和精確定位兩種服務[1]。一般民用的是標準定位，這種定位效果較差，定位精度一般都在10 m左右[2-7]。無法滿足數據鏈時間同步、空中加油、編隊飛行、飛機進場著陸等高精度應用場景。因此，如何在現有條件下提高定位精度，成為人們研究的重點。差分定位技術的出現，很好的解決了這個問題。早期的差分定位技術多使用偽距差分定位[8-9]，這種差分定位解算簡單，定位精度能達到米級，甚至亞米級。能很好滿足民用甚至大部分軍用需求。但是依然無法滿足數據鏈同步這種需要厘米級、甚至毫米級的高精度定位需求。載波相位差分定位技術應運而生了[10]。這種差分定位技術能夠達到厘米級甚至毫米級的精度，但是載波相位的整周模糊度的計算卻是一個難點！ lambda算法[11-12]的出現，很好的解決了這個問題。lambda算法的搜索空間復雜度跟共視衛星數（實際為參與計算的頻點數）的多少成正相關性。即共視衛星數越多，搜索空間越大，lambda解算頻率降低，甚至會出現無法解算的情況。無法滿足飛機進場著陸這種高實時、高精度定位的場景。

為解決上述問題，本文提出了一種頻點裁剪算法，縮小lambda算法的搜索空間，有效地提高定位頻率，但是不降低定位精度。

1 載波相位差分定位的頻點裁剪算法

本節首先簡要介紹載波相位雙差知識，指出lambda算法搜索空間受到頻點參數的影響，然后引入頻點裁剪算法思路。

1.1 載波相位差分定位算法

如圖1所示，載波相位差分定位技術是利用用戶和基準站同時接收衛星信號，基準站播放差分校準數據和位置信息給用戶，用戶根據接收到的衛星信號和基準站的差分校準信息進行差分計算。由于基準站位置提前精確測量，因此，只要計算得到和基準站的相對距離，就能獲得精確的用戶位置信息。

圖1 衛星和接收機關系圖

一般地，記基準站r或用戶u到衛星i的載波相位測量值為：

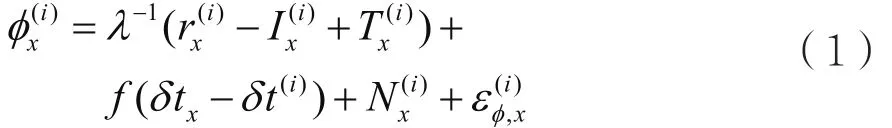
其中：x表示基準站r或者用戶表示接收機x到衛星i的載波相位測量值；λ表示載波波長；表示接收機x到衛星i的幾何距離；表示接收機x到衛星i的電離層誤差；表示接收機x到衛星i的對流層誤差；f表示載波頻率；δtx表示接收機x的鐘差；δt(i)表示衛星i的鐘差；表示接收機x接收到衛星i載波相位的整周模糊度；表示接收機x與衛星i的其他誤差值。

以基準站為參考，將用戶接收機u與基準站r對衛星i的載波相位測量值做差，得到：

通過式（3）可以發現，單差消除了衛星鐘差影響。當用戶和基準站位置較近時，單差的電離層誤差幾乎為零，又由于兩者位于同一高度，故對流層誤差也同樣趨于零。因此得到：

接著，再以基準站和用戶的共視衛星i作為參考，利用共視衛星j的單差載波相位測量值再進行一次求差，得到：

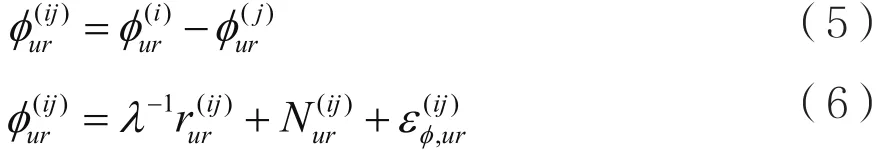
通過式（6）發現，雙差消除了接收機鐘差誤差。假設基準站和用戶某時刻共有M顆衛星，則有：

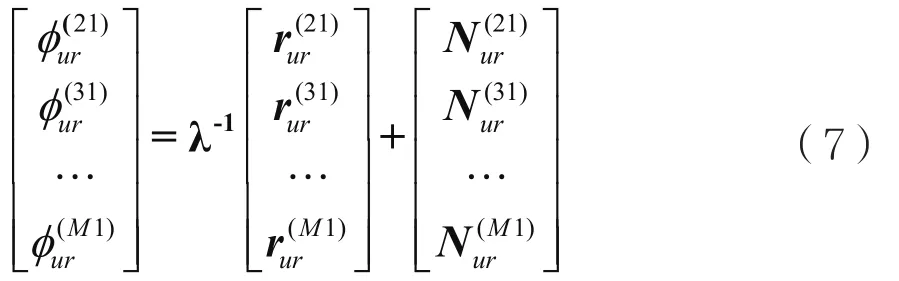
考慮到載波相位差分實際求解的是用戶u與基準站r之間的相對距離。當用戶和基準站之間距離較短時，可以認為用戶和基準站相對于衛星來說，處于平行的位置上，由圖1所示的向量關系得到：

將式（8）帶入式（7）得到：

通過式（9）可知：載波相位雙差觀測方程的維度直接和共視衛星數M相關，M越大，可用頻點數越多，觀測方程的維數越高，求取整周模糊度N的難度也就越大。

1.2 頻點裁剪算法

通過1.1節了解到雙差載波相位定位的求解和用戶與基準站的共視衛星數直接相關。特別是在多系統聯合定位時，共視衛星成倍增長，對于定位的精度沒有實質的提升效果，但是大大增加了整周模糊度的求解難度。如何在不降低定位精度的條件下，提高求解整周模糊度的效率是本文需要解決的問題。

考慮到接收機接收衛星信號時，容易受到大氣層，建筑物等的影響。使得接收到的信號強度有強有弱，同一顆衛星不同頻點的信噪比也會有所不同。例如：參與定位的GPS系統使用的L1和L3雙頻點定位，那么式（9）的實際維數為2M-2維，即每使用一個頻點的載波信號量參與計算，就會增加一個緯度。實際定位過程中，并不需要所有有效信號的頻點數據都參與計算，只需要足夠的頻點數，能夠計算出基線向量值，就可以保證求的用戶的精確位置。所以，考慮對參與定位的頻點進行裁剪，提高計算效率，減少冗余數據。

記接收機收到衛星i、頻點fj的信噪比為其中，M表示基準站和用戶的共視衛星數。j表示使用的頻點，這里默認使用的雙頻定位系統。設頻點信噪比剔除門限為Thd。參與計算的頻點數為CALn。信噪比越高的頻點，它受到外界的干擾就越小。故裁剪頻點的原則是優先裁剪信噪比差的頻點。

首先將參與計算的頻點對應的信噪比值按從低到高的順序進行排序，得到：[SNR1,SNR2,…,SNR2(M-1)]。

最后，剔除不需要參與計算的頻點。分為兩步：

第一步：剔除小于AVGca值的頻點，得到[SNRk,SNRk+1,…,SNR2(M-1)]，其中SNRk-1＜AVGca＜SNRk。此時，剩余頻點數為2M-k-1。

第二步：如果2M-k-1大于CALn，則信噪比值由低到高依次剔除2M-k-1-CALn個頻點，得到[SNR2M-1-CALn,SNR2M-CALn,…,SNR2(M-1)]。如果2M-k-1小于等于CALn，則不做處理。

2 算法驗證

基于上述裁剪算法思路，利用GNSS模擬器同時向地面站和移動站發送衛星射頻信號。模擬器周期100ms輸出地心地固（Earth-Centered，Earthfixed，ECEF）坐標系下移動站位置信息。地面站周期500ms向移動站播報差分校正數據。移動站根據衛星信號和差分校正數據，進行載波相位差分計算。移動站周期500 ms輸出ECEF坐標系下定位結果和當前歷元定位時間，數據記錄到設備自帶的flash中，供事后分析使用。地面站和移動站均使用NovAtel公司的OEM628板卡提供原始觀測量數據。具體設置參數：地面站：圓周運動，圓心位置：N36°，E116°，海拔高189.609 m，橢球高200.6 m，圓半徑1 800 m，速度300 m/s。移動站：圓周運動，圓心位置：N36°，E116°，海拔高2 000 m，橢球高2 010.991 m，圓半徑1 800 m，速度300 m/s。基線長度范圍：12.048～12.051 km。GNS S模擬器信號功率設置為相對功率-35 dBm。移動站定位計算使用的是Xilinx公司的ZYNQ7020芯片自帶的ARM CortexTM-A9核作為處理器。解算時間利用FPGA做的時鐘計數，精度為μs級，Thd=30。

如圖2、圖3、表1所示的測試結果。其中圖3的位置誤差信息是差分定位數據與GNSS模擬器輸出數據在對應時間點之差。

圖2 定位算法耗時

圖3 定位算法精度

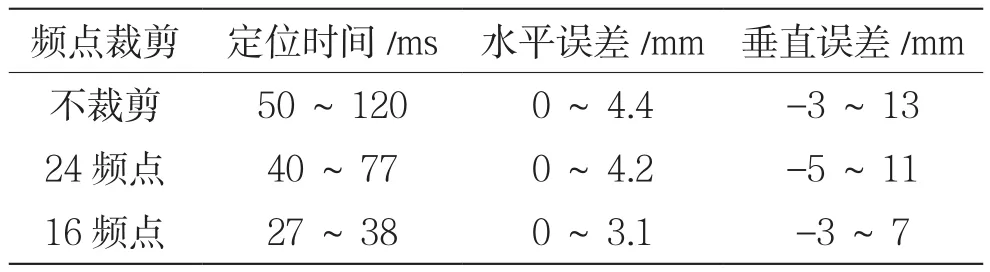
表1 測試結果

圖2和表1表明，隨著頻點數的減少，定位時間顯著減少。時間由50～120 ms減少到27～38 ms。圖3和表1表明，雖然頻點數減少，但是定位結果的水平誤差和垂直誤差并沒有受到影響。水平誤差在0～4 mm，精度達到mm級；垂直誤差在-5～13 mm，精度達到cm級。所以，頻點裁剪算法對載波相位差分定位頻率提升有效。

3 結 語

隨著聯合定位系統的廣泛應用，人們對高精度、高效率的定位要求也越來越高。通過對定位頻點數的裁剪，有效地提高了定位效率，同時又能很好的滿足高精度的定位需求。為高精度、高效率定位提供了一種新的思路。