非正交信號的IC檢測算法研究*

劉 莎 ，陳立萬 ，陳 強 ，李洪兵

（1.重慶三峽學院三峽庫區(qū)地質(zhì)環(huán)境監(jiān)測與災害預警重慶市重點實驗室，重慶 404100；2.重慶三峽學院 教師教育學院，重慶 404100；3.重慶三峽學院物聯(lián)網(wǎng)與智能控制技術(shù)重慶市工程研究中心，重慶 404100）

0 引 言

未來通信網(wǎng)絡(luò)的發(fā)展，第五代移動通信（5G）以后，用戶需求將大大超過網(wǎng)絡(luò)總供應量，并且將有更多的設(shè)備連接到網(wǎng)絡(luò)，這就需要重新審視網(wǎng)絡(luò)的各個方面，從物理層及其基本信號到符合物聯(lián)網(wǎng)（Internet of Things，IoT）范式愿景的網(wǎng)絡(luò)架構(gòu)和信息處理技術(shù)[1-2]。在多載波無線傳輸系統(tǒng)中，正交頻分復用（Orthogonal Frequency Division Multiplexing，OFDM）技術(shù)已廣泛地應用于多個通信標準中。盡管正交傳輸系統(tǒng)，能通過更高階的調(diào)制方式可以有效地提升頻譜效率，但是高階調(diào)制對信道噪聲更加敏感，并且對通信設(shè)備的要求也更為苛刻。

考慮到正交系統(tǒng)的局限性，在2002年首次提出了一種稱為快速正交頻分復用（Fast-Orthogonal Frequency Division Multiplexing，F(xiàn)ast-OFDM）的半正交系統(tǒng)[3]，通過將子載波間的距離減半來提供兩倍的OFDM頻譜效率，但這僅適用于有限的調(diào)制方式。Fast-OFDM現(xiàn)在廣泛應用于光學系統(tǒng)[4-6]。這種復用方案將子載波間隔減少到傳統(tǒng)OFDM的50%。隨后，1975年重新研究了一種稱為多流超奈奎斯特（Fast than Nyquist，F(xiàn)TN）的技術(shù)[7]，并給出了理論和仿真結(jié)果[8]，2003年提出了一種稱為高頻譜效率頻分復用（Spectrally Efficient Frequency Division Multiplexing，SEFDM）的非正交多載波系統(tǒng)[9]。SEFDM在保持每個子載波具有相同傳輸速率的同時，通過違反子載波間正交性原則，壓縮了子載波間的距離，從而獲得更高的頻譜效率（Spectral efficiency，SE）。SEFDM技術(shù)是在頻域內(nèi)打破Nyquist準則，實現(xiàn)在頻域內(nèi)的超Nyquist傳輸，是一種多載波FTN傳輸技術(shù)。

1 SEFDM信號模型

與OFDM信號類似，SEFDM是將一組具有N個正交幅度調(diào)制（Quadrature Amplitude Modulation，QAM）的復數(shù)信號分成并行的N組數(shù)據(jù)流，并將這N組數(shù)據(jù)流調(diào)制到SEFDM的非正交重疊子載波上。因此，對于具有N個子載波的SEFDM系統(tǒng)，其歸一化信號可以表示為：

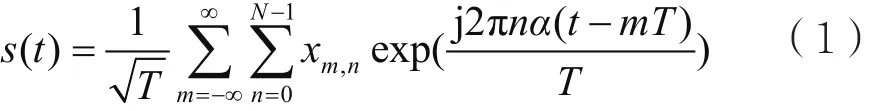
其中，Δf是子載波間隔；T是SEFDM信號的周期；xm,n是第t個SEFDM信號中第n個子載波上調(diào)制的復 QAM信號；α=Δf T（0＜α≤1）是帶寬壓縮因子，它的大小表示頻譜壓縮的程度即在相同的條件下，SEFDM信號比OFDM信號節(jié)省了(1-α)×100%的帶寬，當α=1時，表示沒有壓縮，即SEFDM信號退化為OFDM信號。OFDM信號和SEFDM信號的頻譜圖如圖1所示。

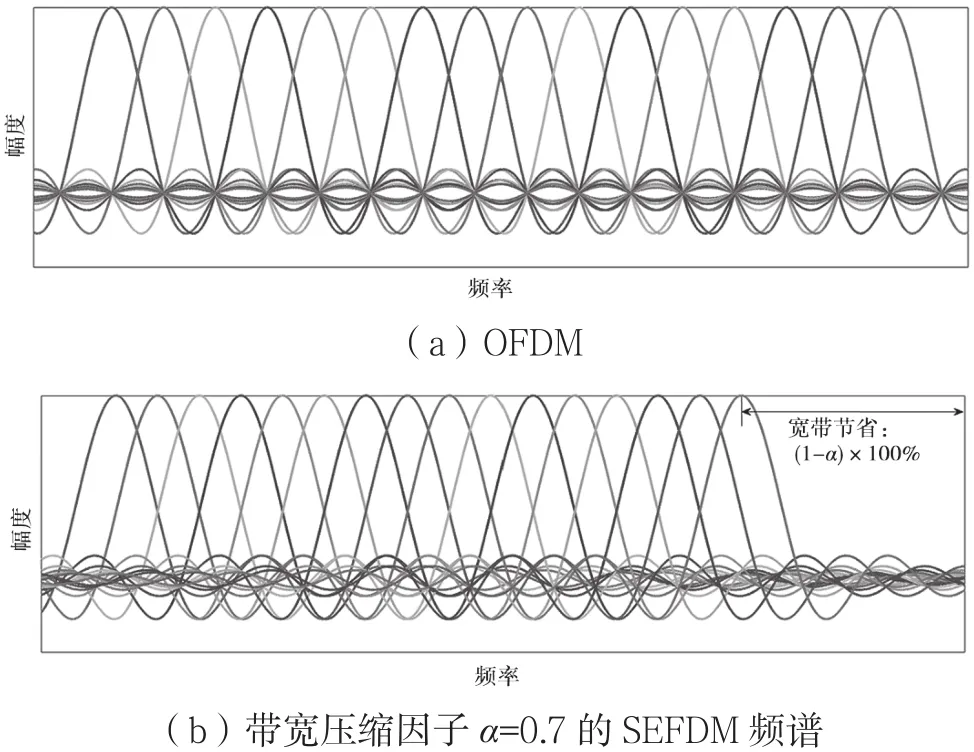
圖1 OFDM信號和SEFDM信號的16個重疊子載波的頻譜

不失一般性地，為了簡化運算，在一個符號周期T內(nèi)對SEFDM信號進行討論。取m=0時的SEFDM符號，有：

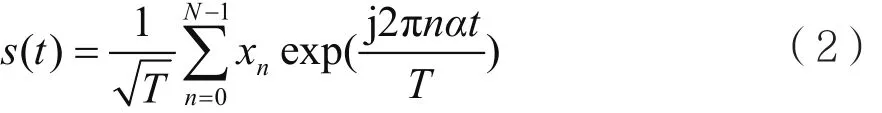
由于實際的系統(tǒng)處理的都是離散信號，因此，有必要對SEFDM系統(tǒng)的離散信號模型進行研究。通過對式（2）中的連續(xù)信號s(t)作Q點的等間隔采樣，可以得到離散的SEFDM信號：

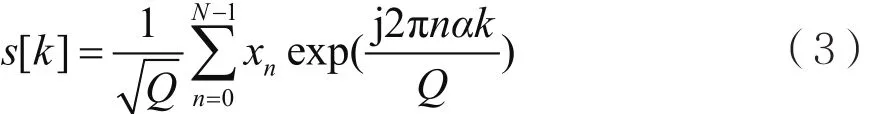
其中，s[k]是s(t)的第k個時間樣本，k=[0,1,…,Q-1]；xn是在第n個子載波上調(diào)制的QAM符號，并且是歸一化縮放因子。采樣間隔為采樣點數(shù)Q=ρN，ρ表示過采樣因子且ρ≥1。

將式（3）用矩陣形式可以描述為：

其中，X表示N維的QAM符號向量X=(x0,x1,x2,…,xN-1)T；S表示Q維的信號采樣點向量S=(s0,s1,s2,…,sQ-1)T；Φ是Q×N維的子載波矩陣：

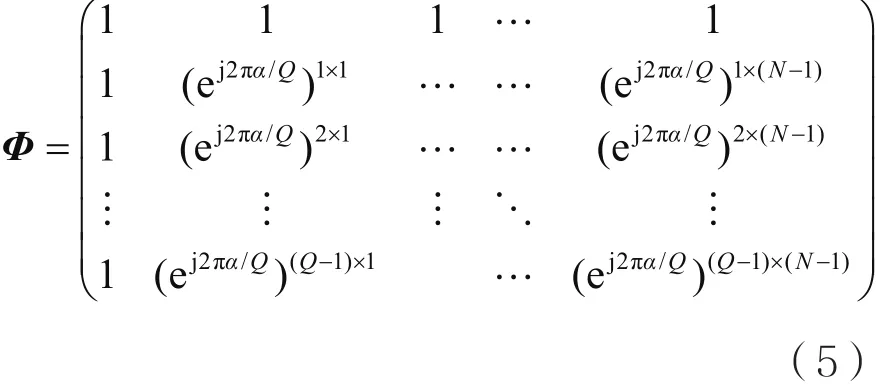
考慮任意兩個子載波向量：

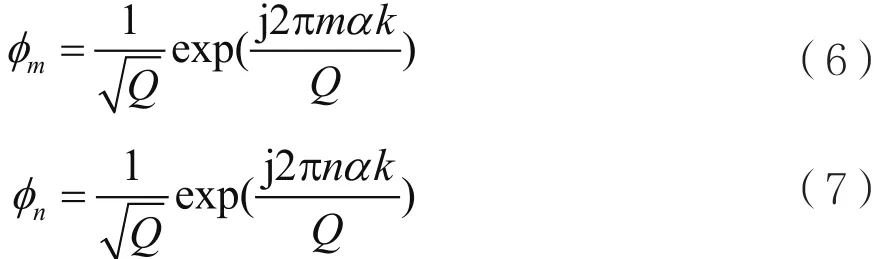
其中，k=0,1,...,Q-1，m,n=0,1,...,N-1，他們之間的互相關(guān)系數(shù)為：

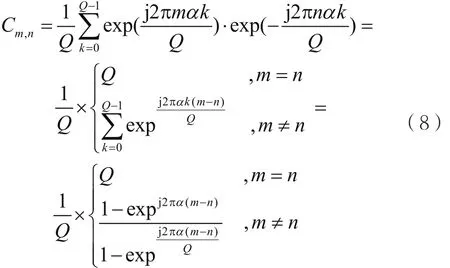
OFDM系統(tǒng)通常是通過離散傅里葉逆變換/離散傅里葉變換（Inverse Discrete Fourier Transform/Discrete Fourier Transform，IDFT/DFT）來實現(xiàn)的，由于SEFDM系統(tǒng)的子載波間缺乏正交性，需要對輸入的符號序列作一些處理后，再利用IDFT/DFT來實現(xiàn)。在加性高斯白噪聲（Additive White Gaussian Noise，AWGN）信道下，SEFDM信號的最終接收符號表示為

其中，X是發(fā)送符號的序列，R是接受符號序列，W是接收端的噪聲向量，C是IDFT/DFT矩陣表達式，其非對角項表示非正交子載波重疊造成的子載波間干擾（Inter Carrier Interference，ICI）。

由于接收端引入了嚴重的ICI，增加了矩陣C的條件數(shù)，將會影響系統(tǒng)的誤碼性能。子載波數(shù)量與矩陣C的條件數(shù)的變化關(guān)系如圖2所示。

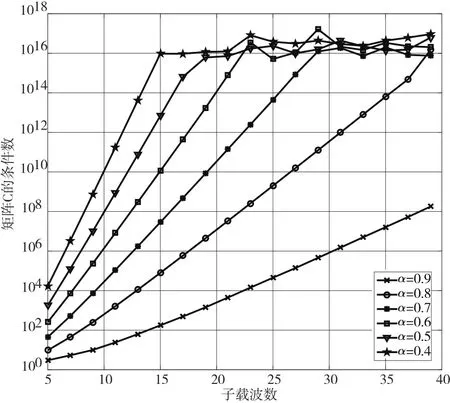
圖2 不同α下子載波數(shù)量與矩陣C的條件數(shù)的變化關(guān)系

2 迭代消除（IC）檢測算法

當有噪聲干擾下，根據(jù)施密特正交化，SEFDM信號的接收符號表示為[10]：

其中，M是矩陣C經(jīng)過QR分解后的上三角矩陣R，即：

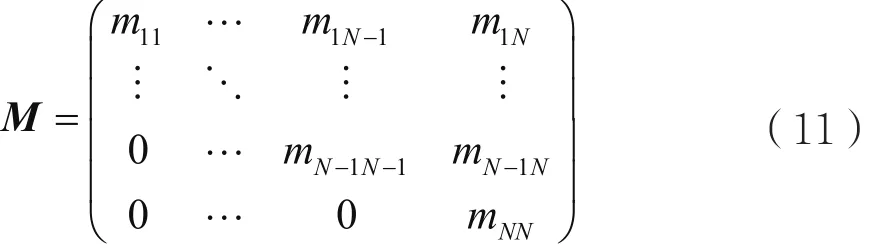
從第n個符號開始，第n個傳輸符號的估計值為：

第n-1個傳輸符號的估計值為：

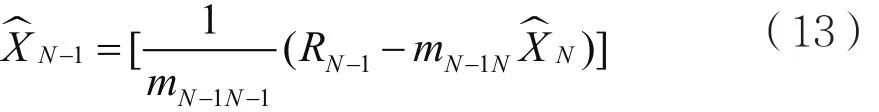
第i（i=1,2,...,N）個元素的估計為：

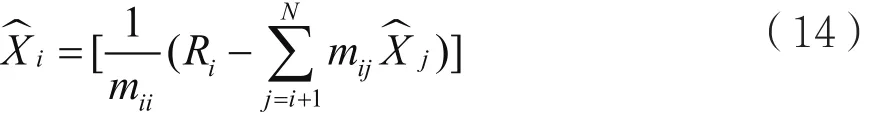
以此類推，直到第一個元素。

迭代消除（Iterative Cancellation，IC）檢測算法的結(jié)構(gòu)框圖如圖3所示。

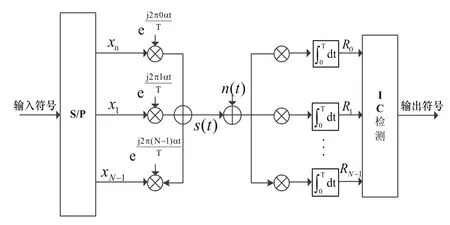
圖3 IC檢測算法的結(jié)構(gòu)框圖

3 仿真結(jié)果及分析

（1）不同子載波個數(shù)下的誤碼率仿真

不同子載波個數(shù)的誤碼率仿真參數(shù)如表1所示。

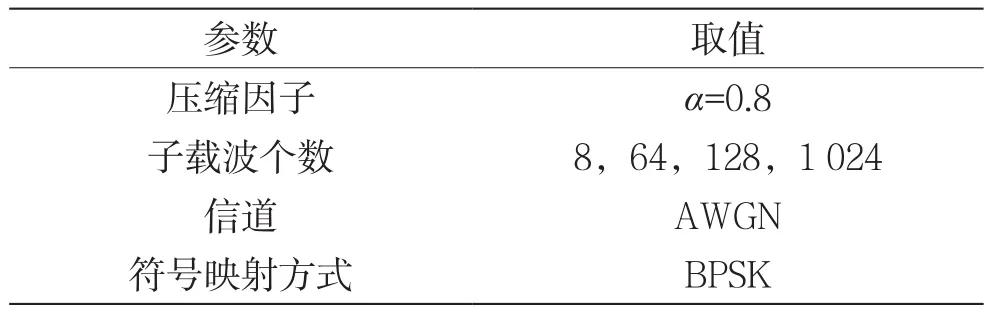
表1 不同子載波個數(shù)的仿真參數(shù)設(shè)置

（2）不同壓縮因子下的誤碼率仿真

不同壓縮因子的仿真參數(shù)如表2所示。

表2 不同壓縮因子的仿真參數(shù)設(shè)置

圖4顯示了不同子載波個數(shù)對系統(tǒng)誤碼率性能的影響。隨著子載波個數(shù)的增加，系統(tǒng)的誤碼性能有所降低；而當子載波個數(shù)增加到一定程度時，系統(tǒng)的誤碼性能不會隨著子載波個數(shù)的增加而趨于穩(wěn)定。圖5顯示了不同壓縮因子對系統(tǒng)誤碼率性能的影響。在其余條件相同的條件下，隨著壓縮因子的減小，即相鄰子載波之間的間隔減小，系統(tǒng)的誤碼性能逐漸降低。然而，壓縮因子α=0.6時的誤碼性能僅次于α=0.9時的誤碼性能，此時帶寬壓縮最大，且?guī)捁?jié)省了40%。

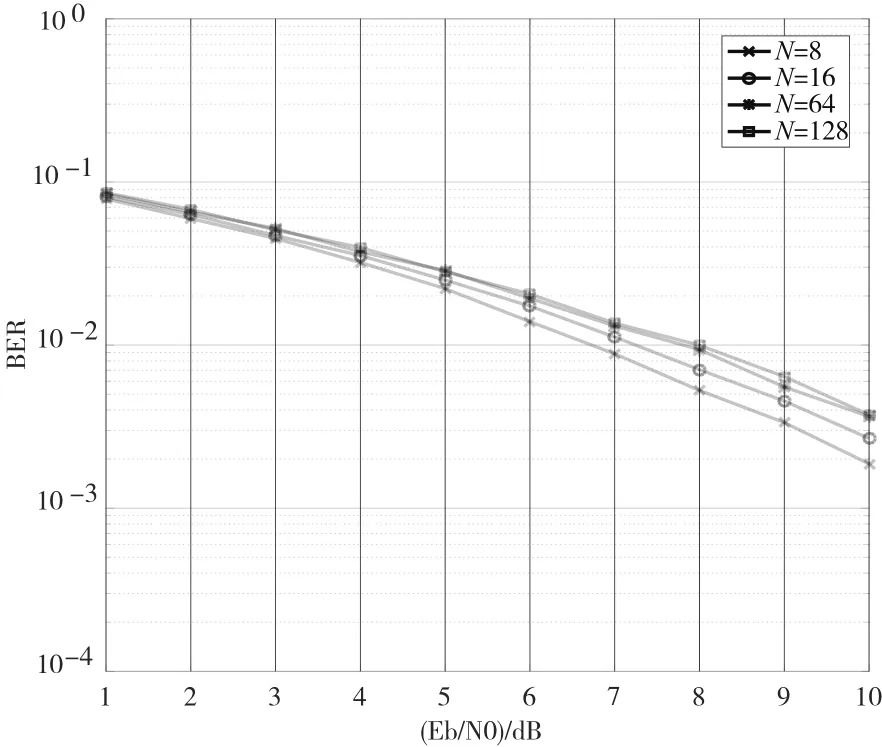
圖4 不同子載波個數(shù)下IC檢測算法的誤碼率曲線

圖5 不同壓縮因子下IC檢測算法的誤碼率曲線

4 結(jié) 語

針對SEFDM打破了正交性，引入強烈的子載波間干擾，對SEFDM接收端信號檢測帶來了許多困難的問題，本文研究了一種IC檢測算法。仿真結(jié)果分別從不同子載波個數(shù)和不同壓縮因子下的誤碼率性能進行了比較。結(jié)果表明IC檢測算法在隨著子載波個數(shù)增加的條件下誤碼率性能較優(yōu)，但其在不同壓縮因子條件下，壓縮因子α=0.6時的性能最優(yōu)，且?guī)捁?jié)省40%。