基于長短記憶網絡的艦船航跡預測方法?

楊金鴻 皇甫立 熊 璋 許 松 王新遠

（1.中國船舶工業系統工程研究院 北京 100094）（2.北京航空航天大學 北京 100191）

1 引言

艦船航跡預測在艦船航行跟蹤、防止撞擊、事故預警、調度分配、航行決策支持、海洋交通管制等各方面發揮著重要作用［1］。目前針對艦船航跡預測的方法主要包括：基于數學方程的方法、基于灰色系統的方法和基于馬爾科夫的方法［2］。傳統基于數學方程的航跡預測主要采用卡爾曼濾波［3］、粒子濾波等方法［4］，這些方法通過建立運動學［5～6］或動力學［7］數學方程刻畫艦船運動過程。在理想的環境下，這些數學方程能夠精準地計算艦船運動航跡。然而，眾所周知，海洋環境復雜多變，海風、海況、水流等諸多環境因素對艦船運動影響較大。并且諸多干擾因素之間相互影響、互相干擾，進一步加劇了艦船運動的復雜性。傳統的數學方程難以考慮海風、海況、水流等諸多環境因素的影響。基于灰色系統的方法通過分析系統因素間的關聯關系，建立相應的微分方程模型，從而預測事物未來發展趨勢的狀況［8］。目前使用最廣泛的灰色預測模型是關于數列預測的單變量、一階微分GM（1，1）模型。GM（1，1）模型的基本假設是：將系統原始時間序列按時間維度進行累加，累加后的時間序列呈現的規律可用一階線性微分方程的解來逼近。經理論研究，由一階線性微分方程逼近擬合的原始時間序列呈指數變化規律。因此，當原始時間序列隱含著指數變化規律時，灰色模型GM（1，1）的預測是非常有效的。基于馬爾科夫鏈的預測方法將航跡預測問題轉化為狀態轉移問題，根據歷史數據求解狀態轉移概率矩陣，依據當前狀態預測下一時刻的狀態。

隨著人工智能技術的迅速發展，智能技術成為解決不確定問題的重要途徑，在解決諸多實際問題中發揮著重要作用［9］。在基于神經網絡的航跡預測方面，徐婷婷提出基于BP神經網絡的艦船航跡實時預測方法［10］，該方法建立輸入層、隱藏層和輸出層三層神經網絡結構，以航向、航速為輸入，預測下一個時間周期的經度差、緯度差。然而BP神經網絡的方法僅僅利用當前時刻的航向、航速預測下一時刻的偏移量，而無法利用任何短期歷史信息。

近年來提出的深度學習方法是一種具備多層感知的深度網絡模型，具有強大的非線性處理能力和良好的“記憶”性質［11］。長短記憶網絡作為一種經典的深度學習算法，能夠較好地刻畫時間序列系統內部發展規律，預測時間序列系統發展趨勢［12］。目前LSTM已廣泛應用于語音識別、翻譯、時間序列預測等領域。艦船航跡具有明顯的平滑性，下一時刻的位置狀態由歷史時刻的位置滑行而來。可見，利用艦船歷史時刻位置預測下一時刻的位置狀態，將有利于提高航跡預測的精度。在復雜的海洋環境中，在一定時間內海況信息是類似的，下一時刻的船舶運動狀態不僅與當前時刻有關，而且與歷史時刻也有關。LSTM是一種時間序列預測方法，與基于BP神經的預測方法相比，基于LSTM的方法能夠預測更長的周期。文獻［11］提出基于循環神經網的軌跡預測方法，對用戶出行的軌跡地點進行預測。但是該方法主要針對商廈、學校、地鐵站、公司、加油站等離散的軌跡位置狀態進行預測。艦船航跡分布于連續時間空間中，具有明顯的時空連續性，如何對時空連續航跡進行預測需要進一步研究。本文首先提出連續位置向量化方法，構建長短記憶網絡模型，提出基于滑動窗口的LSTM航跡預測算法，利用歷史航跡數據訓練LSTM模型，采用滑動窗口的方法預測未來時間周期數據。實驗仿真三種典型的艦船機動場景，結果驗證了本文所提方法的有效性。

2 基于長短記憶網絡的艦船航跡預測算法

2.1 LSTM航跡預測模型

LSTM作為一種經典的循環神經網絡，將上一個時間周期的輸出作為下一個時間周期的輸入，如圖1所示為按時間展開的循環神經網絡模型。LSTM單元主要由輸入門、輸出門、遺忘門和輸入節點等組成，LSTM的記憶細胞結構如圖2所示。

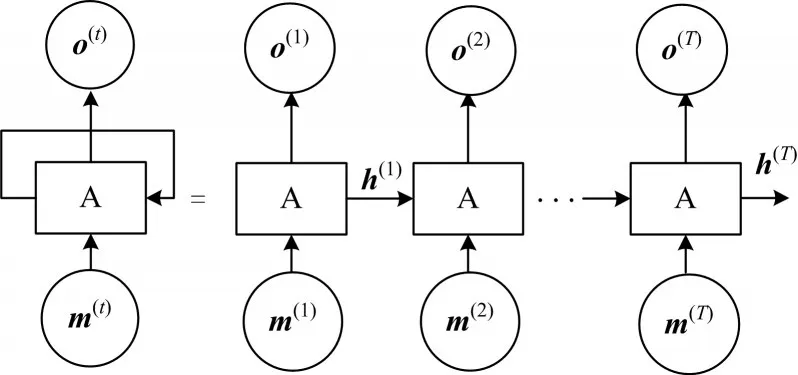
圖1 LSTM網絡概略圖

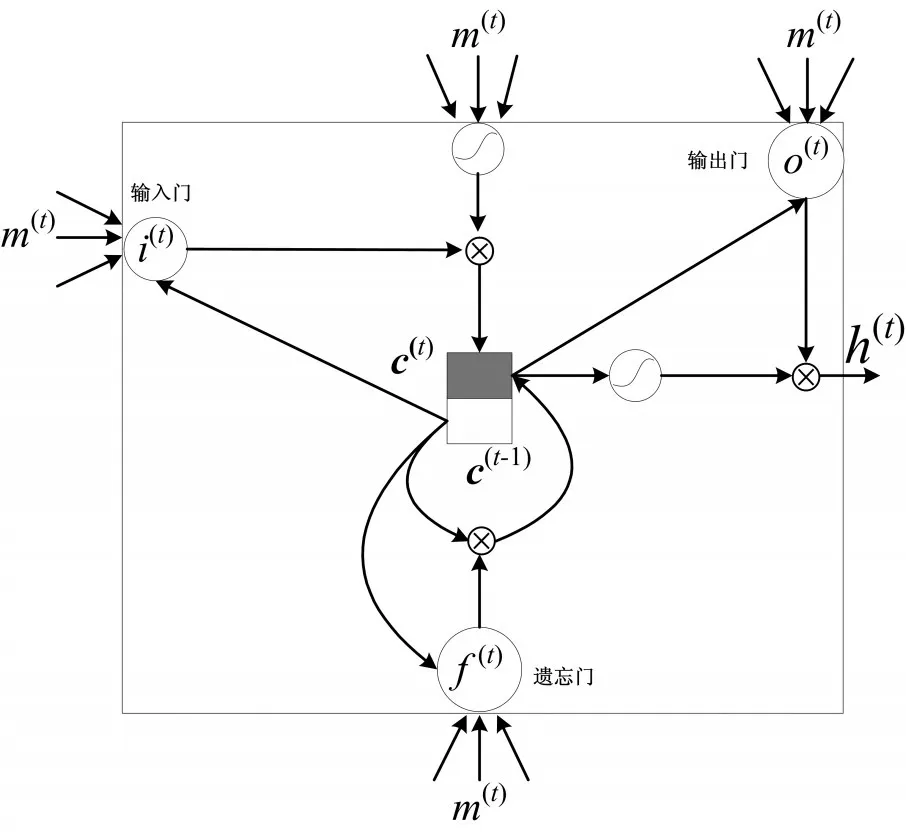
圖2 長短期記憶神經網絡記憶細胞結構

其中c為記憶單元，i為輸入門，o為輸出門，f為遺忘門，o為記憶單元輸出，t表示時間周期。假設輸入向量m(t)=(θ(t)，v(t))表示第t個時間周期的輸入向量的集合，h（t）表示第t個時間周期的隱藏層狀態，i（t）表示第 t個時間周期的輸入門的輸出狀態，f（t）表示第t個時間周期遺忘門的輸出狀態，o（t）表示第t個時間周期輸出門的輸出狀態，c（t）表示第 t個時間周期記憶門的輸出狀態，那么其定義可分別表示為

其中，σ是sigmoid函數。b表示偏置量。W表示權重向量，利用權值矩陣的下標表示矩陣具體含義，例如Whi代表的就是隱藏層與輸入門的權值矩陣。在此基礎上，可通過式（1）～（5）計算并更新LSTM單元在每一時刻的狀態。

在復雜的海洋環境中，不同時刻船舶運動狀態之間存在復雜的非線性關系，利用神經網絡擬合歷史時刻運動狀態與下一時刻船舶運動狀態之間的關系。在基于LSTM模型的預測中，將船舶航行的歷史運動狀態輸入模型中，預測下一個時間周期船舶運動狀態。已知探測到艦船在1至T時刻的運動狀態信息，根據時間上的有序形式組成的運動狀態序列集合稱為M（Motion Elements）。

定義1（運動狀態序列集）對船舶的運動狀態建模，利用每個時間艦船航行方向和速度組成運動狀態序列：

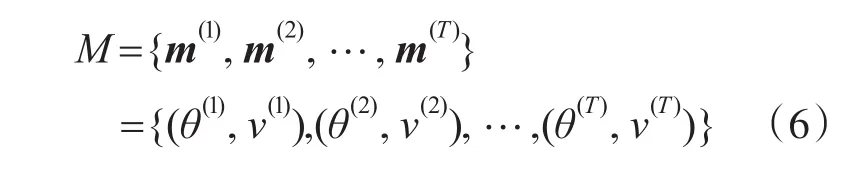
其中 θ(t)（1≤t≤T ，0≤θ(t)≤2π）表示船舶在t時刻的航向與Y軸的夾角，v(t)表示艦船在t時刻的航行速度，稱M為運動狀態序列集。

每個神經元由兩個輸入端、兩個輸出端組成；m(t)=(θ(t)，v(t))是模型的輸入，o(t)=((t)，(t))為模型的輸出。連續的航跡預測分為若干離散時間周期，為了預測多個時間周期的運動航跡，定義每個時間周期的船位差序列集如下：

定義2（船位差序列集）對艦船的船位差進行建模，利用X與Y兩個方向上的矢量表示船位差：

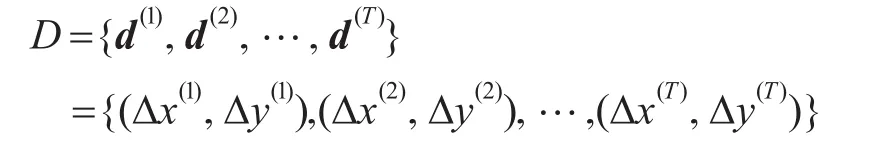
其中Δx(t)（1≤t≤T）表示艦船在時間周期t時刻的在X軸的船位差的投影，Δy(t)（1≤t≤T）表示艦船在時間周期t時刻的在Y軸的船位差的投影。Δx和Δy分別表示艦船運動的橫坐標船位差和縱坐標船位差。根據模型的輸出o（t）計算每個時間周期的船位差如下：

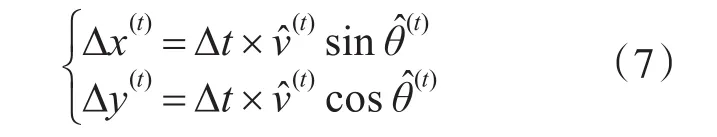
根據船位差序列預測t時刻船舶的位置如下：

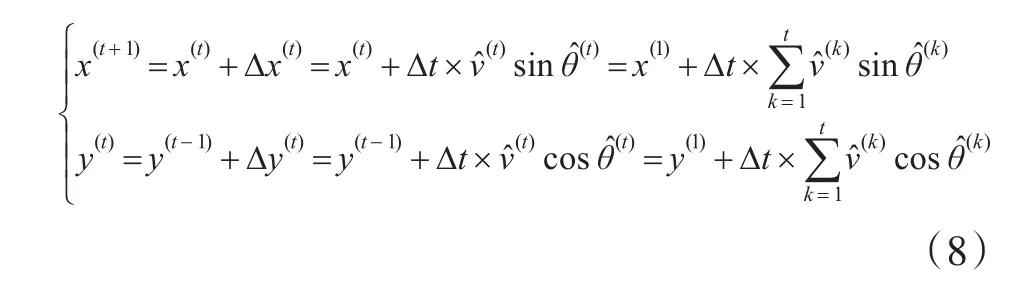
2.2 基于滑動窗口的LSTM航跡預測模型

為了對更長的時間周期進行預測，提出基于滑動窗口的LSTM預測模型。假設可以得到的實時觀測運動狀態序列個數為T，選取長度為N的滑窗。以滑窗的長度限制輸入訓練序列的長度，避免迭代過程中學習時間過長。為了進行中長期預測，可以采用迭代法對滑窗中的樣本進行更新。假設需要預測l步航跡，則通過每次迭代，對第i（i=1，2，3，…，l）步的預測值替換滑窗中最舊的數據，每替換一次便讓LSTM網絡進行一次新的學習，更新網絡結構，以新的網絡結構進行下一步的預測。滑窗樣本替換方法如圖3所示。

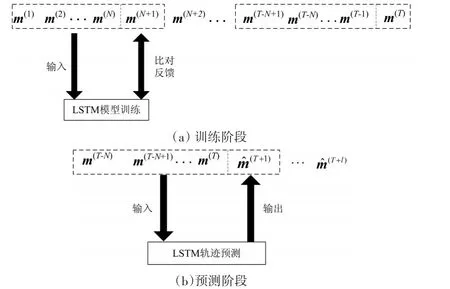
圖3 基于滑動窗口的LSTM模型

在訓練階段：將探測到的歷史數據進行分組，每組N+1個數據，前N個數據作為輸入數據，預測第N+1個數據值，與第N+1個數據的真實值做對比誤差，迭代調整網絡參數，如圖3（a）。

在預測階段：利用探測到的第T-N至T個數據預測未來第T+1時刻的數據，再由T-N+1至T+1個數據預測第T+2個數據，直至預測未來l個數據，如圖 3（b）。

3 仿真驗證

為了驗證本文所提方法的有效性，選取三種典型的航行應用場景，分別是左滿舵、右滿舵和S型航線航行。本實驗將前70%時間周期作為訓練樣本，預測后30%時間周期的航跡。通過與真實航跡對比，分析LSTM方法和灰色系統模型GM（1，1）的預測效果。

定義3（預測均方誤差）對于預測軌跡點與實際軌跡點的幾何空間誤差采用式（5）所示的均方根誤差RMSE來計算：

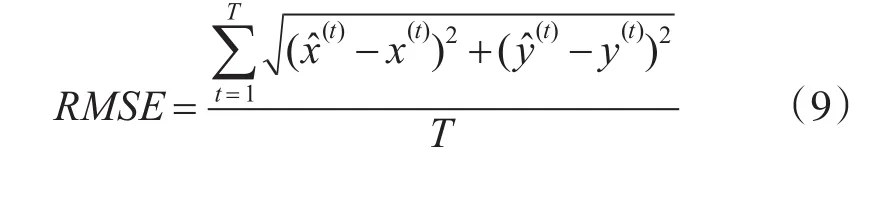
其中，（ x(t)，y(t)）表示實際軌跡點的位置，（(t)，(t)）表示預測軌跡點的位置信息，T表示預測軌跡點的時間周期數量。

如圖4所示為真實航跡以及灰色系統和LSTM的航跡預測結果。結果表明，與灰色系統預測方法相比，LSTM預測結果更接近于真實航跡。圖5所示為每個時間周期灰色系統和LSTM預測位置的距離誤差，總體結果表明LSTM的預測誤差明顯低于灰色系統方法。圖6所示為灰色系統和LSTM預測的均方誤差，對比分析結果表明LSTM的預測精度優于灰色系統方法，原因是LSTM具有較強的記憶能力，能夠記憶歷史時刻航跡位置，推斷航跡變化趨勢，具有較好的預測能力。長短期記憶神經網絡采用一個特定的記憶細胞存儲信息，對于存在依賴關系的歷史信息有著非常重要的作用。通過引入輸入門、輸出門和遺忘門，LSTM有效提高了面對具有長時依賴性時序數據的學習、分析能力，所以LSTM對于處理變長序列的效果是非常好的。

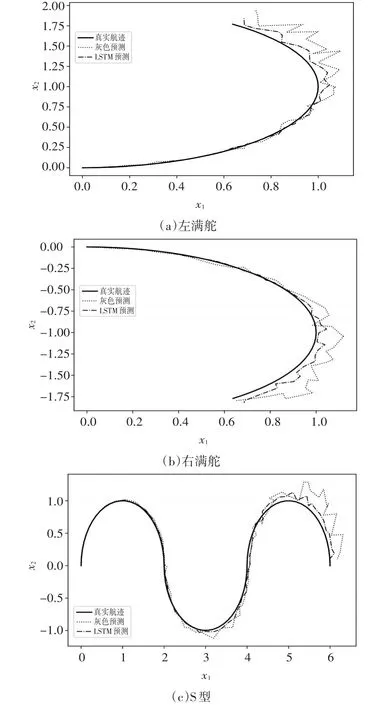
圖4 航跡預測結果對比

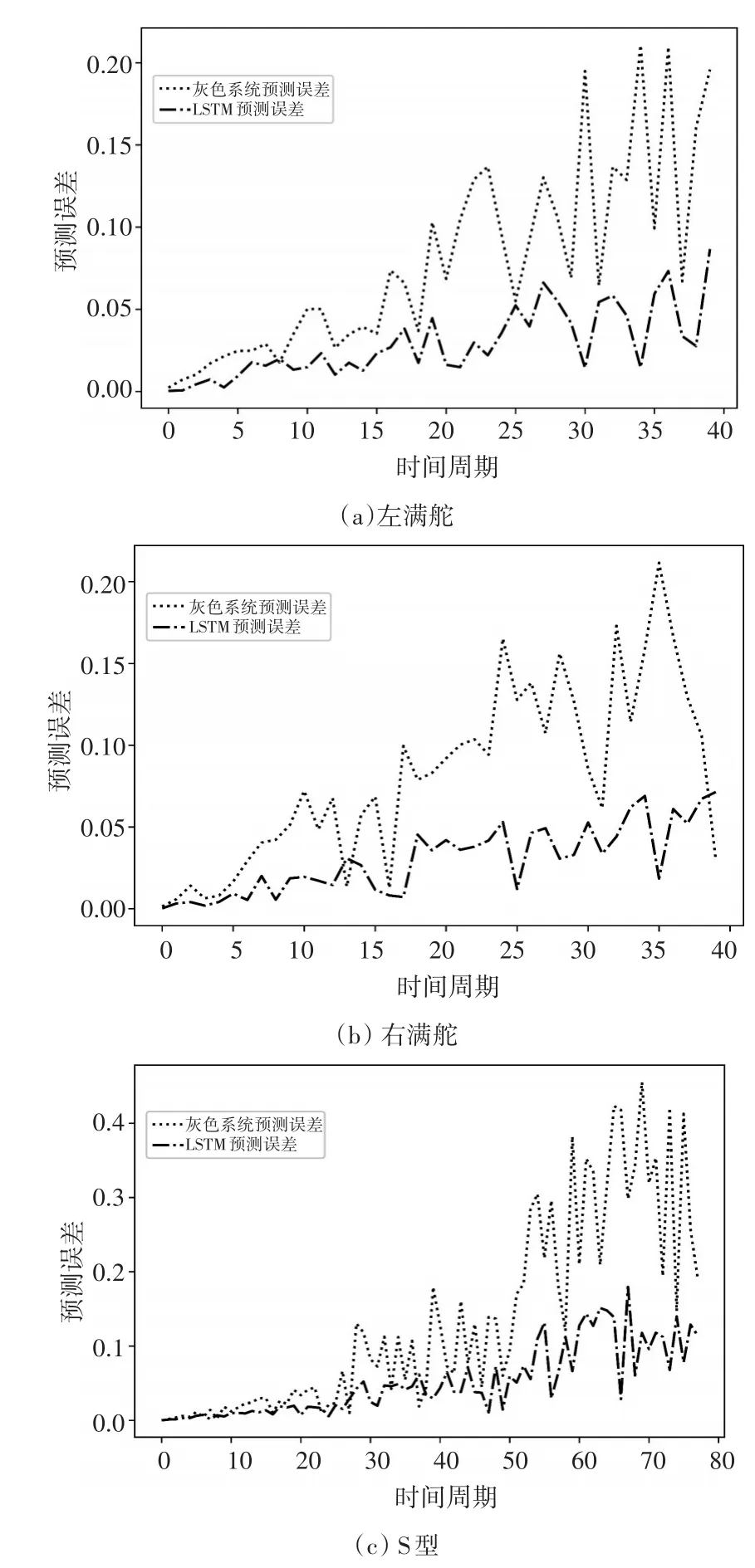
圖5 預測距離誤差

圖6 均方誤差對比

4 結語

采用LSTM來解決艦船的軌跡預測問題。研究結果表明，針對艦船不同的航行場景，提出的方法在預測精度方面均高于灰色系統預測方法。可見依靠LSTM解決艦船的軌跡預測具有很好的應用前景。下一步考慮將艦船運動方程融入到LSTM模型中，進一步提高LSTM的艦船航跡預測精度。