多層熱防護服一維瞬態導熱優化模型

朱家明，左正東，杜佳軒，王浩歌

（1.安徽財經大學 統計與應用數學學院，蚌埠 233030；2.安徽財經大學 金融學院，蚌埠 233030）

大量的科學統計研究表明，高溫極端環境會使暴露其中的工作人員發生中暑等癥狀，各地方政府推出了“高溫限工令”，即規定氣溫超過35℃的，要避免11：00-15：00室外露天和高處作業，此項舉措對保護工作人員的健康和權益方面有一定的積極作用［1］。體表溫度作為人體生理指標之一［2］，在室內熱環境學、生理學等領域有著重要的研究意義。通過探究多層熱防護服一維瞬態導熱規律，在生產設計高溫熱防護服方面有一定的借鑒意義。

數據來源于2018年高教杯全國大學生數學建模比賽A題，為了便于解決問題，提出了如下假設：（1）無內熱源且初始溫度均勻分布；（2）材料成本與厚度成正比；（3）熱量傳遞的方向視為一維垂直于皮膚表面輻射；（4）熱防護服裝的織物各項指標性質相同；（5）該模型僅考慮熱傳遞；（6）傳導和輻射在織物中熱傳遞是均勻的；（7）防護服最外層和人體皮膚傳遞過程中的輻射可以忽略；（8）空氣層的厚度值不超過6.4mm（忽略熱對流影響）；（9）織物與織物間，織物與外界空氣間，空氣與人體皮膚之間的溫度變化連續的且梯度跳躍。

目前關于熱防護服內部傳熱模型根據熱防護服材料層數分為單層和多層模型。單層熱防服模型只有外殼，國內外學者主要研究外界環境的輻射熱量、織物性質、空氣層厚度對防護服熱性能的影響［3］。Gibson［4］首先提出高溫單層多孔介質傳熱傳質模型，Torvi［5］考慮不同輻射強度對熱防服內部熱傳遞的影響。Ghazy［6］利用單層織物中熱傳導及比熱采用經驗公式，將常量轉為變量，更好地擬合了高溫情況的熱傳遞過程。

許多學者在單層模型的基礎上改進并探究了熱防護服熱濕傳遞多層模型。Mell［7］提出了多層面料模型層與層之間的傳熱模型。Mercer［8］和Ahmed Elgafy［9］考慮到由于相變材料對防護服的熱防護效果的影響，建立了內含相變材料的多層動態熱傳遞模型。

1 基于傅里葉定律和COMSOL仿真模型對溫度分布的計算

1.1 研究思路

首先分析單層無限長圓筒溫度分布的一般情況。以此為基礎進一步探討一維平板穩態線性變溫導熱率的情況下的溫度分布，根據邊界條件引出四種組合，再建立非線性方程組，通過求解雅克比矩陣，并使用牛頓迭代法求解，給出溫度位置分布函數。考慮到不同層厚度差異較大，同層不同厚度的位置其溫度存在著差別，為了更加準確地計算溫度分布狀況，將層數進行進一步細化，利用COMSOL軟件進行仿真，得到各個厚度位置的每秒具體的溫度值，可以直觀地看出傳熱過程。織物厚度越厚，隔熱效果越好，皮膚表面溫度也越低。對第II層進行掃描。改變第II層和第IV層的厚度時，從節約材料的角度考慮，應該盡可能減少第II層的厚度，增大第IV層的厚度，以達到相同的效果。首先固定第II層的厚度，改變第IV層的厚度。最大的第IV層厚度的同時也須保證第II層厚度最小，此時為最優值。

1.2 模型的建立與分析

1.2.1 溫度的時間空間分布

為了簡化問題，假設人為半徑220mm，高1700mm的圓柱，當人穿著防護服時，在柱坐標系下類似于多層圓筒壁（見圖1），一維非穩態導熱實際上是二維問題，需要考慮時間（單向）和空間坐標。

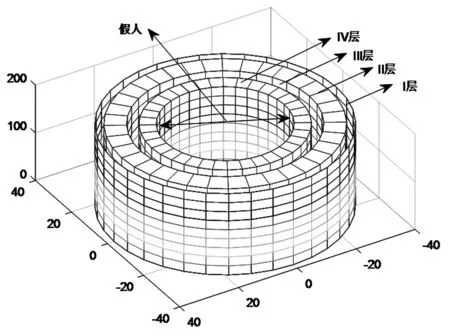
圖1 假人高溫作業專用服裝穿著仿真圖

在圖1中給出了由服裝——皮膚及空氣層組成的系統，其中，防護服通常由三層織物材料構成，記為I、II、III層，其中I層與外界環境接觸，III層與皮膚之間還存在空隙，將此空隙記為IV層。

從外到內，織物距離皮膚的距離以次為d1、d2、d3，材料的熱傳導率以次為k1、k2、k3，表面溫度值以次為T1、T2、T3、T4。如圖2所示。

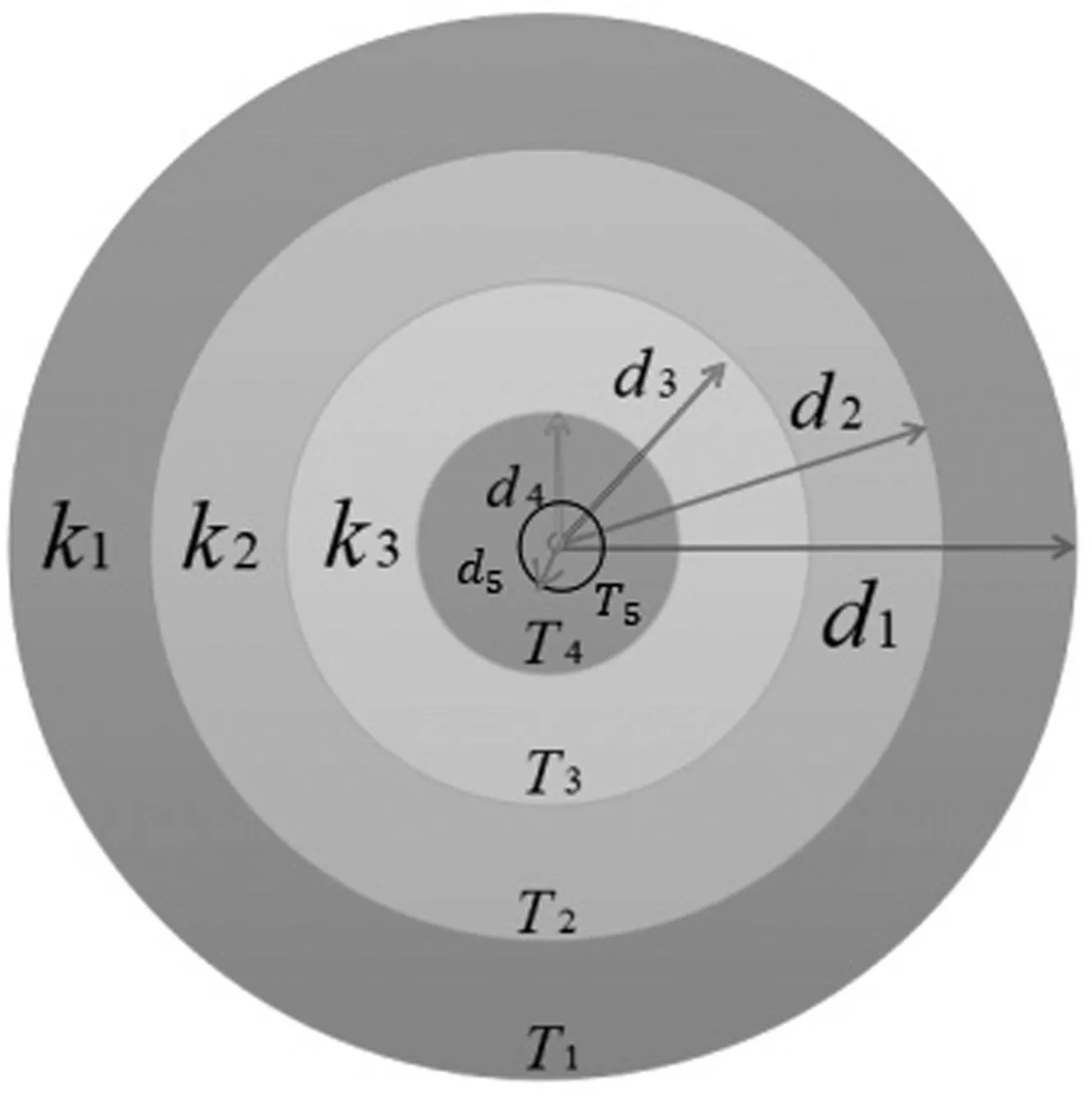
圖2 多層結構溫度分布邊界結構簡圖

其中T1=75℃，T5=37℃ ，d2-d3=6mm ，d4-d5=5mm。

導熱系數的計算式是由傅里葉導熱定律的數學表達式導而出，即：

導熱系數是表示物質導熱能力的大小的一項基本宏觀物理性質。本題中導熱系數被當作常數對待。大部分情況下，導熱系數與溫度呈非線性關系的。通常在實際計算中，若溫度變化范圍不大，其數值可近似采用線性關系，即

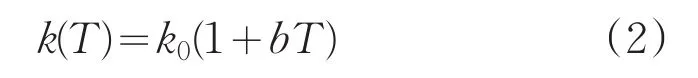
式中，T為溫度，b代表該溫度范圍內導熱系數隨溫度的變化，其值為常量，b＞0時熱導率與溫度成正比，b＜0時熱導率與溫度成反比，b=0時熱導率是常數［10］。

下式中的系數Ai、Bi等值為由邊界條件確定的系數。

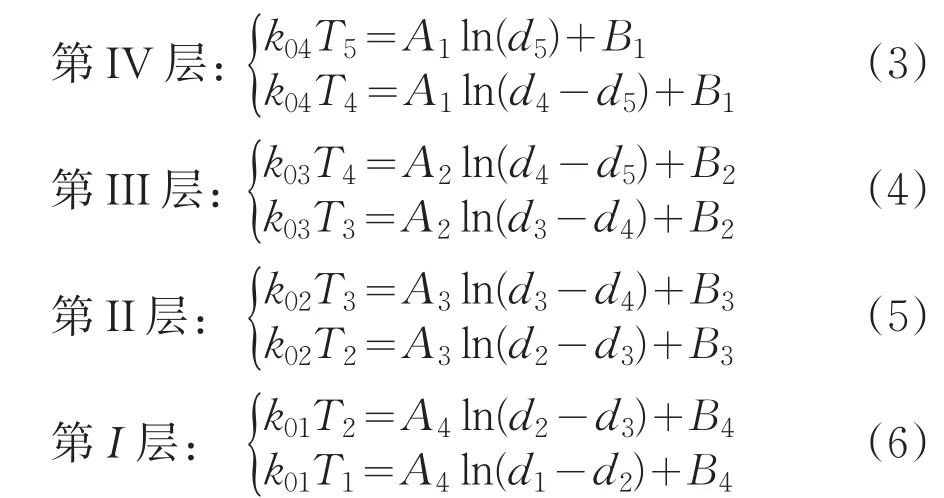
由題可知，兩層織物的熱流密度相等，即

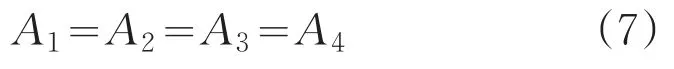
由式（3）、（4）、（5）、（6）整理得：

方程（9）是一個關于中間界面溫度T2、T3的非線性方程組，可用牛頓法解出：

雅克比矩陣為：

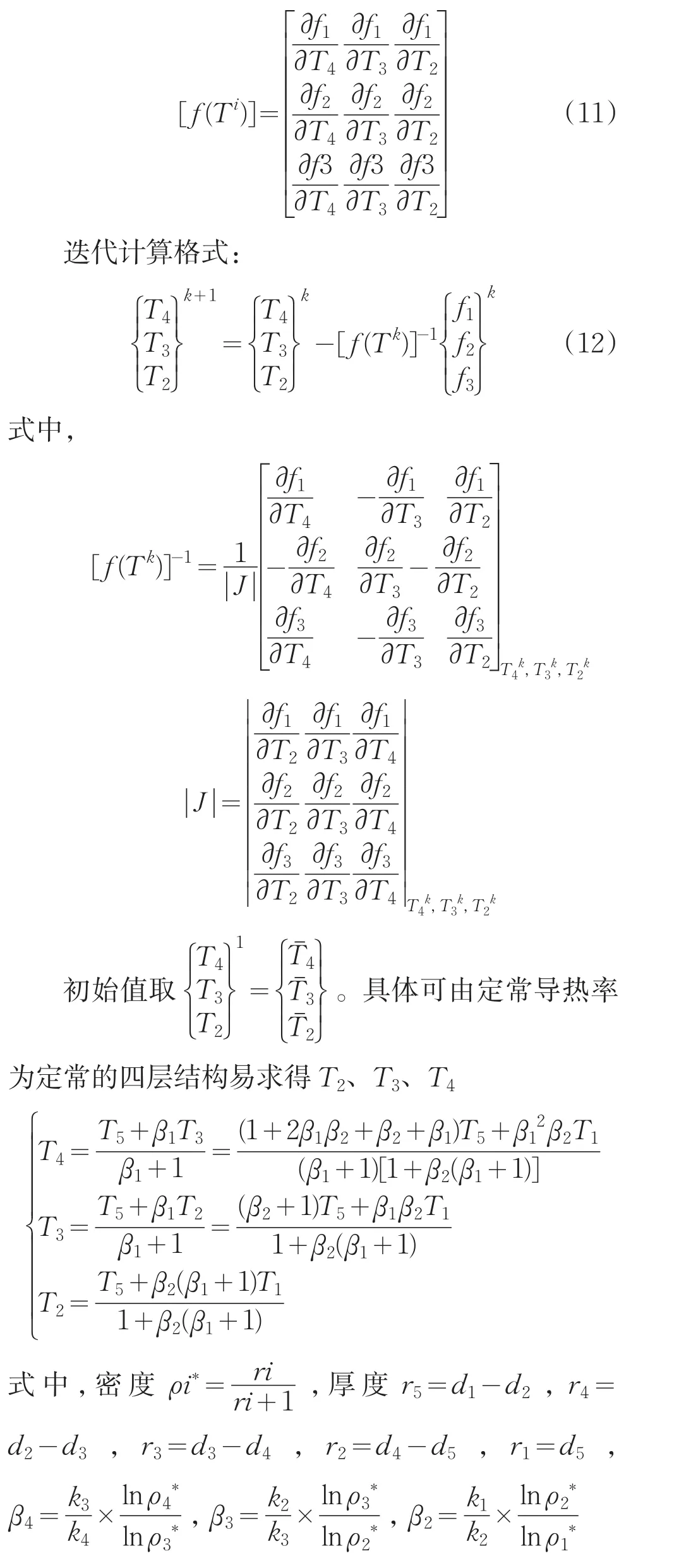
代入（11）迭代，可求得T2、T3、T4，然后計算溫度分布等。

第IV層溫度分布：

考慮到不同層厚度差異較大，同層不同厚度的位置其溫度存在著差別，在（13）-（16）式的基礎之上，為了更加準確地計算溫度分布狀況，將層數進行了進一步細化，選取了52個節點，將0～15.2mm的厚度劃分為了51個細微厚度層，在厚度層內，溫度基本無差異。而多層圓筒壁導熱的一維問題，在垂直導熱的假設前提下，可以進一步簡化為圖3，圖3從左到右衡量分別為I、II、III、IV層，且在51個區間內每秒溫度存在著瞬時變化，每個區間的垂直圓筒壁的溫度在每一秒下是相等的。

圖3 一維簡化仿真圖

利用COMSOL軟件進行仿真，可以得到各個厚度位置的每秒具體的溫度值，將其繪制為溫度隨厚度與時間變化的三維立體圖（圖4），可以更直觀的看出傳熱過程，導熱進行50秒后，初始條件37℃對系統中無量綱分布的影響趨近于0，溫度分布此時主要取決于第三邊界條件的影響。其在1100mm時基本達到穩態，溫度基本保持穩定。溫度時間分布誤差分析如圖5所示。

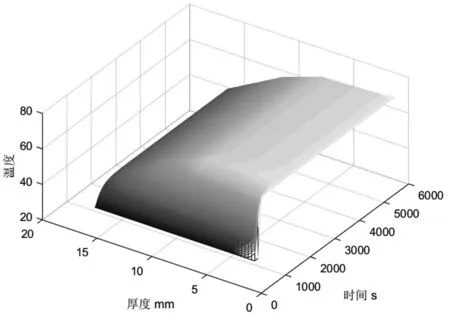
圖4 溫度厚度時間三維坐標系圖

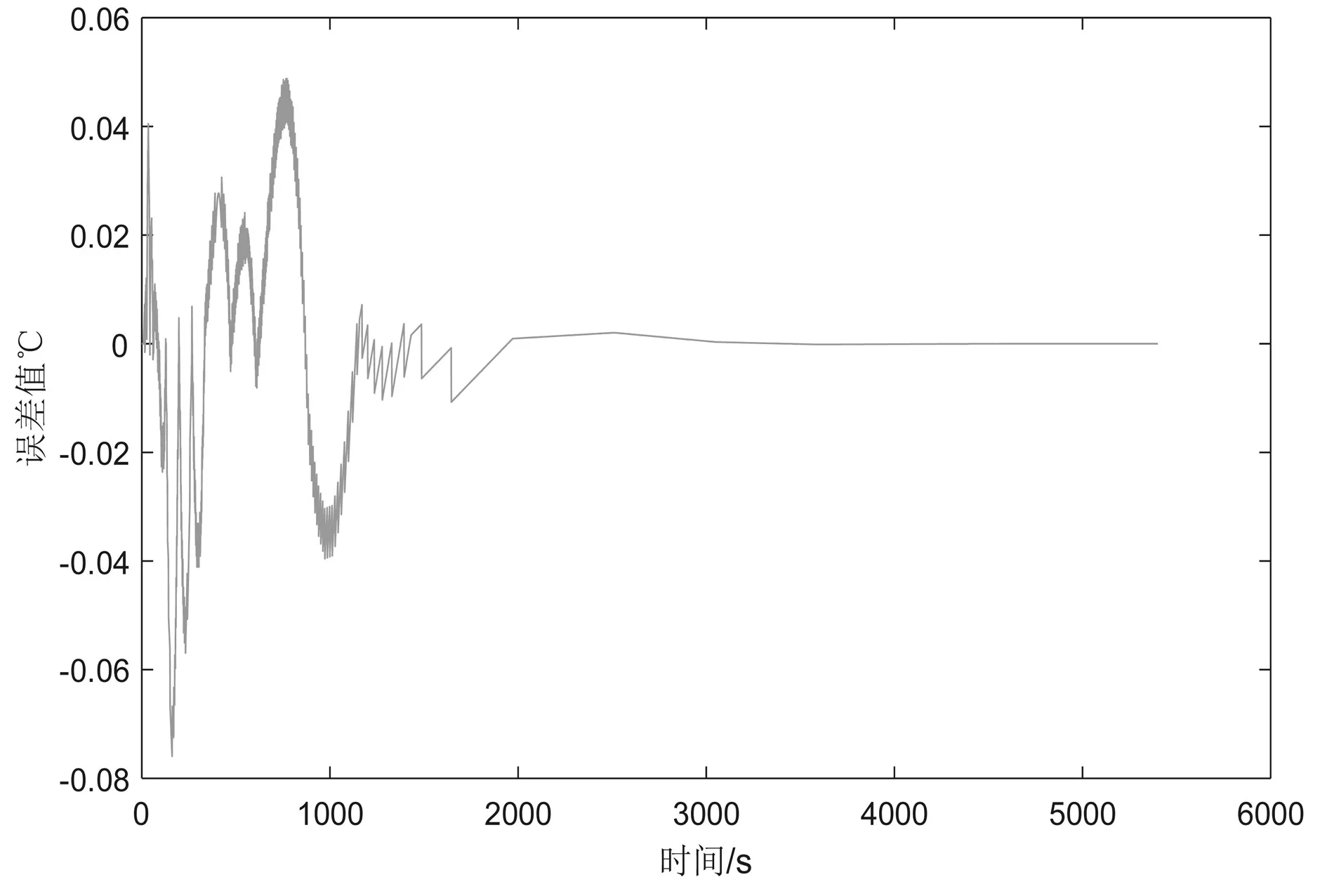
圖5 溫度時間分布誤差分析圖

將所得到的假人皮膚外側的實時溫度值（即厚度為15.2mm處）與數據中給的測定值進行比較（見圖6），可以看出本模型的熱傳導預測效果較好，基本吻合實測值，只在1000秒到1500秒之間略有偏差，因此本模型準確度較高。

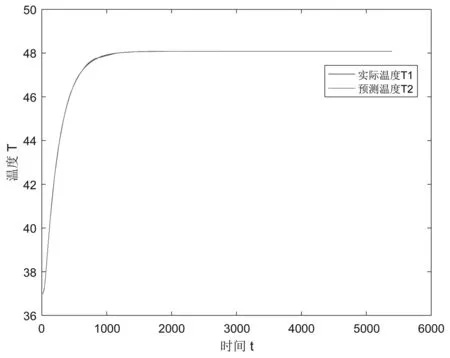
圖6 預測溫度與實際溫度差值相關圖

再利用MATLAB繪制三維等溫線圖（見圖7），在三維空間內的同一等溫線上溫度相等，到達穩態的實際根據厚度的不同而變化。

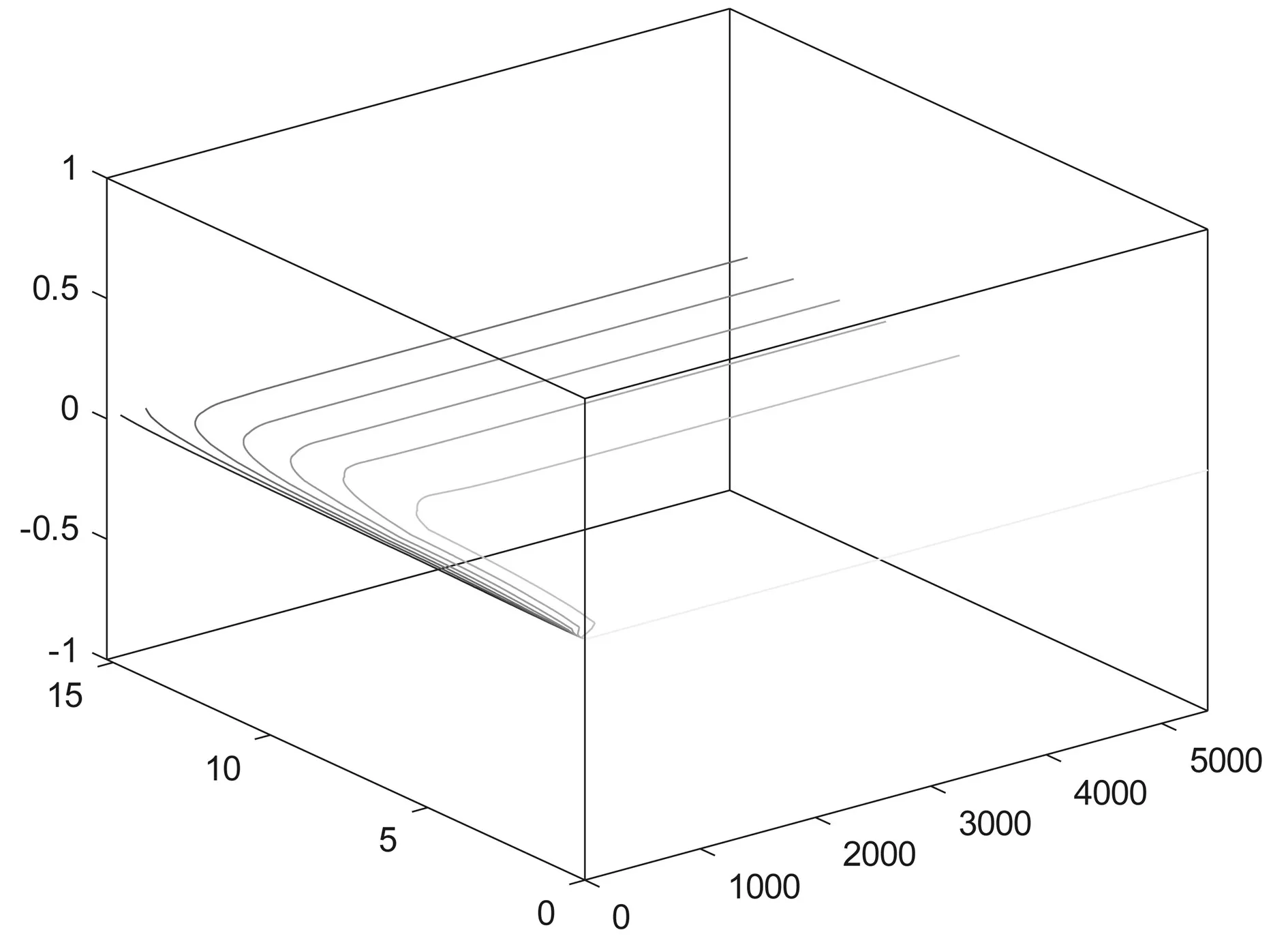
圖7 空間直角坐標材料三維等溫線分布圖

利用COMSOL Multiphysics軟件的一維瞬態無內熱源導入公式（17）（18）：

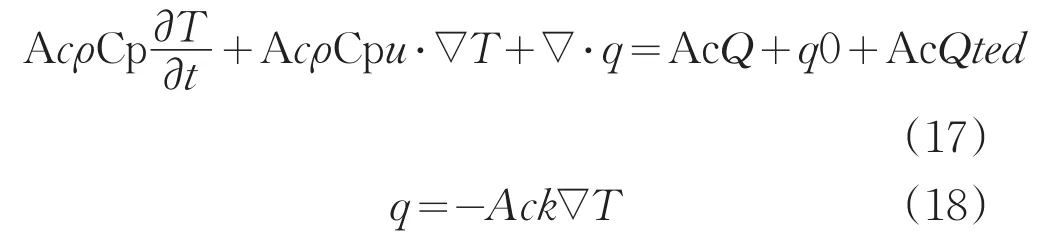
以上是熱傳導方程，Ac是一維線的橫截面積，ρ是密度，Cp是比熱容，T是溫度，t是時間，u是速度，固體不流動，不用考慮。k是導熱系數。等式左邊第一項代表材料溫度改變，第三項代表熱傳遞貢獻，等式右邊是熱量產生，在本模型種并沒有熱量生成，不需要考慮。

1.2.2 基于溫度分布曲線對防熱服厚度的最優設計

織物厚度越厚，隔熱效果越好，假人皮膚外側溫度也越低。

利用之前的函數：

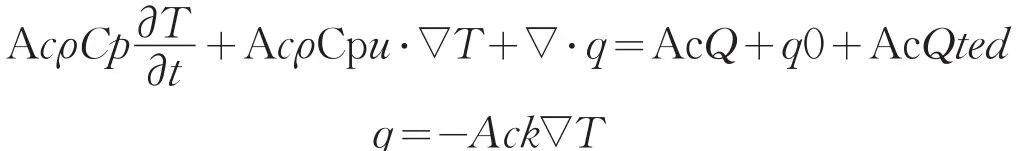
利用局部差分法，對該方程進行二次積分，求出溫度分布的函數：

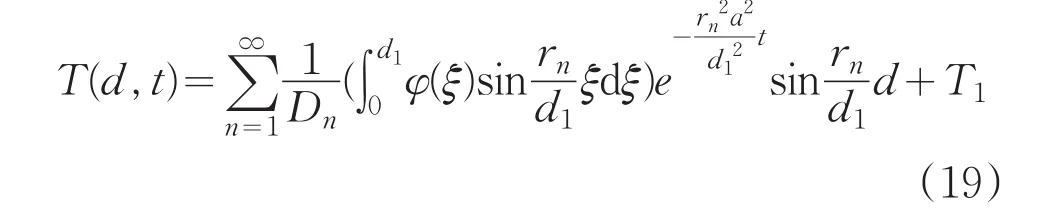
若要求在確保工作60分鐘，假人皮膚外側溫度不超過47℃，且超過44℃的時間不超過5分鐘的情況下，確定第II層的最優厚度。最優厚度即為滿足上述約束條件下的該層最薄厚度，這樣節省材料費用，達到最優，即為求min（d2-d3）。約束條件為：

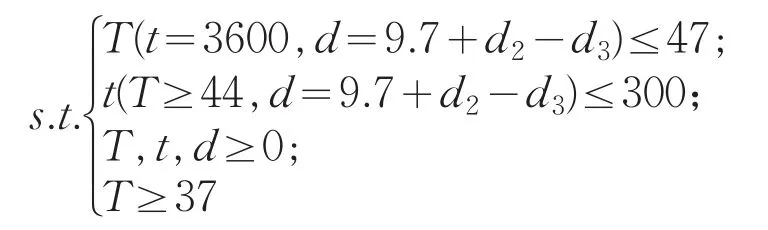
其中，t(T,d)為T(t,d)的相關函數。

1.3 模型結果及分析

在其他變量不變的情況下，在第II層厚度的取值區間內，不斷變換第II層厚度，得到不同厚度下的假人皮膚外側實時溫度分布狀況繪制如圖8所示。

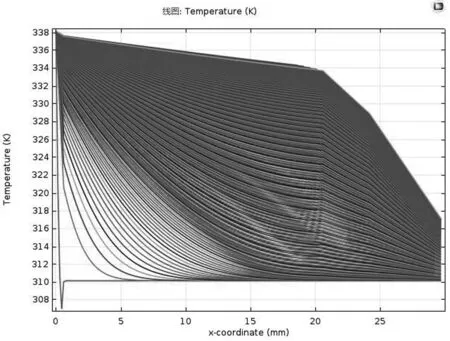
圖8 假人皮膚外側溫度分布曲線圖

結果發現當第II層厚度達到19mm時，在55分鐘時，溫度達到44度，并且在60分鐘時，溫度也只是稍微高于44度，達到臨界值，此時的溫度分布曲線如圖9所示。

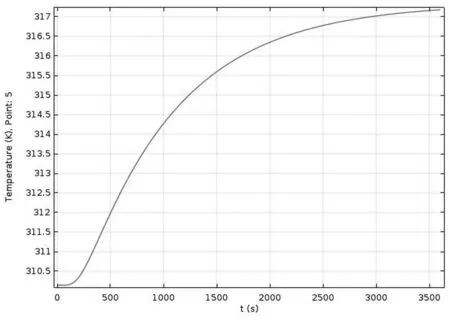
圖9 假人皮膚外側溫度分布曲線圖

為考慮節約材料，最優厚度應該定位在稍厚于19mm的19.5mm。

表1是當第II層厚度為19.5mm時，部分時間的溫度（單位為開爾文）變化。

當第II層和第IV層的厚度時可以改變的，從節約材料的角度考慮，應該盡可能減少第II層的厚度，增大第IV層（該層為空氣層）的厚度，以達到相同的效果。首先固定第II層的厚度，改變第IV層的厚度。假設固定第II層為10mm，逐漸增加第IV層的厚度，通過COMSOL Multiphysics軟件掃描發現當第IV層厚度達到最大值6.4mm時依然不滿足確保工作30分鐘時，假人皮膚外側溫度不超過47℃，且超過44℃的時間不超過5分鐘的條件。具體溫度變化如圖10所示。

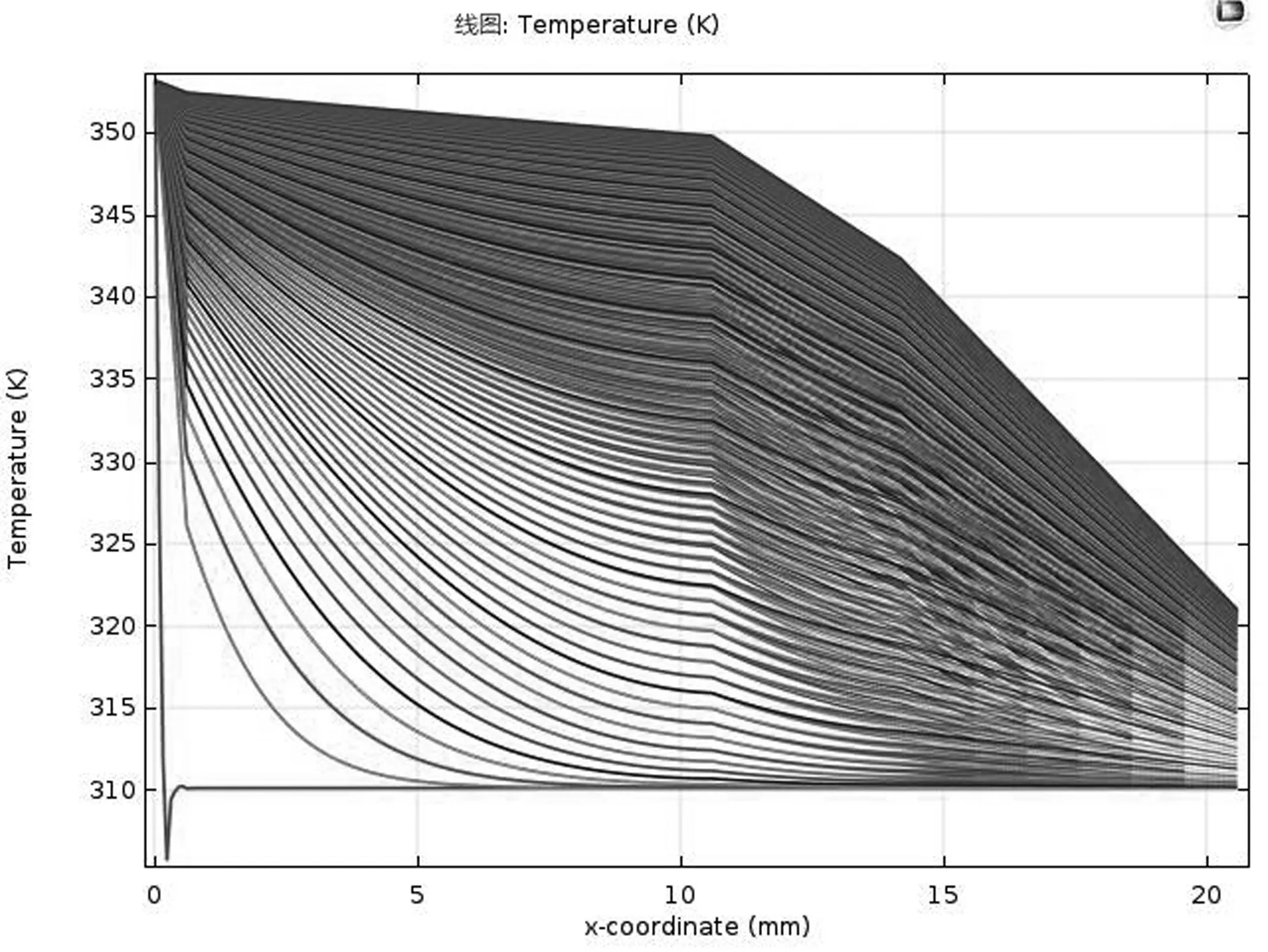
圖10 固定第II層厚度改變第IV層厚度的溫度變化線圖

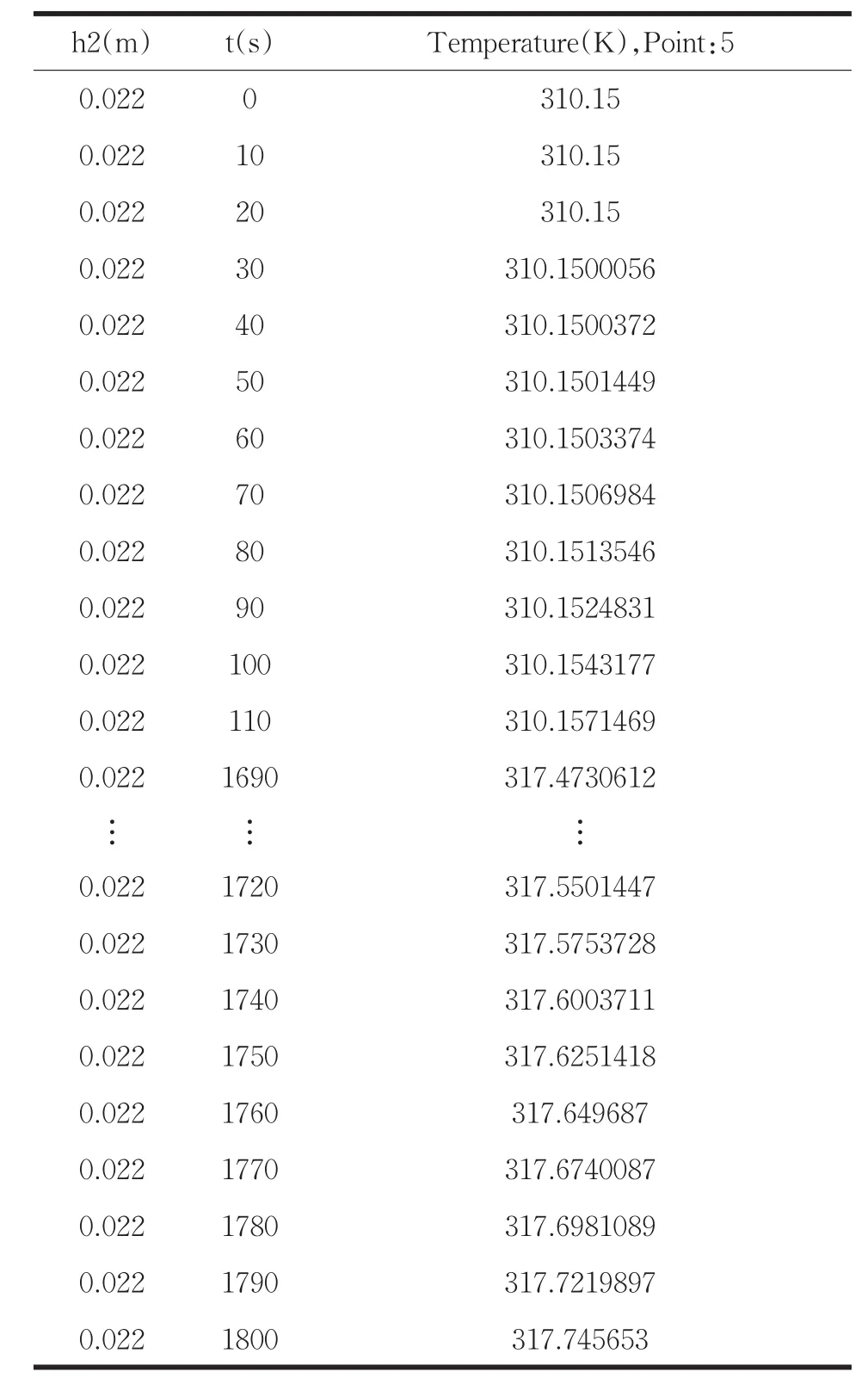
表1 假人皮膚外側溫度隨時間變化一覽表

因此逐漸增加第II層厚度，使得第IV層厚度在最大值6.4mm時，滿足要求條件。最大的第IV層厚度也保證第II層厚度最小，從而達到節約材料的目的。具體溫度變化如圖11所示。

結果發現當第II層厚度為22mm，第IV層厚度為6.4mm時，滿足要求條件，為最優值，溫度曲線如圖12所示。

圖11 固定第IV層厚度改變第II層厚度的溫度變化線圖

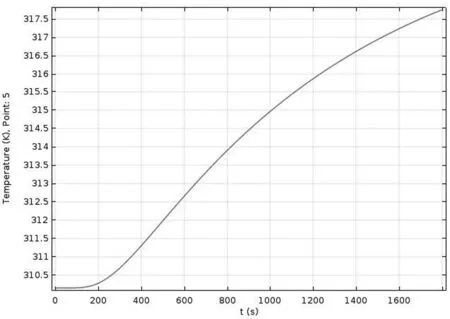
圖12 第IV層、第II層最優厚度的溫度變化線圖

2 結論

基于傳熱學的理論，對不同假設下、不同初始條件、以及不同形式的存在耦合關系的多層圓筒體模型進行探究，以界面溫度為解耦參數，將多層傳熱簡化成單層傳熱問題，從而推導出多層圓筒體在不同邊界條件下的溫度分布表達式。通過借助COMSOL 5.3a軟件，以有限元法為基礎，通過求解偏微分方程來實現真實導熱現象的仿真，將復雜的多層圓筒壁瞬態導熱模型進行簡化，大大降低了計算難度。文中建立的模型與緊密結合實際情況，突出了傳熱系數的作用，充分考慮物理學原理，從而使模型更加通用、易懂。