行星減速器動態特性的響應面近似建模方法研究

楊正龍，陳 娟，康 洪，楊 為

（1.中國北方車輛研究所車輛傳動重點實驗室，北京 100072；2.重慶大學 機械傳動國家重點實驗室，重慶 400044）

0 引言

多級行星傳動系統具有多自由度、多間隙等特點，在嚙合過程時齒輪副的彈性變形、時變嚙合剛度和制造誤差等都會對齒輪動態系統產生很大影響，影響了行星減速器在運轉過程中的平穩性、安全性[1]。因此，行星減速器動態特性研究引起了國內外學者的廣泛關注。李潤芳[2]等運用有限元的方法建立了齒輪系的動力學仿真模型，通過對比實驗和仿真結果來研究內部激勵下的傳動系統動態特性；劉文吉[3]等采用有限元法建立了漸開線少齒差模型，分析了動態齒輪的接觸特性，得到了完整嚙合周期的齒面接觸應力、齒面滑動位移等嚙合特性參數。

響應面法以多項式超曲面近似描述個變量之間的關系[4,5]，形式簡單、計算方便，因此本文提出了基于響應面法建立行星減速器的動力學模型，以行星減速器的特征參數作為變量，以減速器表面的最大加速度為目標函數，建立了行星減速器動力學特性與特征參數之間的關系，有助于深入研究行星減速器的動力學特性。

1 試驗水平和試驗指標

某多級行星減速器主要由太陽輪、行星輪、齒圈、行星架以及箱體組成，其有限元模型如圖1所示。在運轉過程中，為了提高其承載力以及使用壽命，通常將太陽輪、行星輪、內齒圈進行正角度變位，這將避免跟切，減少齒面磨損，且能消除不變位的太陽輪與行星輪及內齒輪之間嚙合的同心條件限制，綜合考慮目標函數和約束條件的要求，選取太陽輪齒數zs，行星輪齒數zp，內齒圈齒數zr，太陽輪變位系數xs，行星輪變位系數xp，內齒圈變位系數xr，模數m和齒寬b。故此8個設計變量可表示為：

圖1 行星減速器有限元模型

行星輪系不等角變位的方法是在太陽輪和內齒圈的齒數不變，而將行星輪的齒數減少1～2的情況下實現的。對于不變位或高變位行星輪系中各齒輪齒數的關系為：zp=（zr-zs）/2，而傳動比和裝配條件又只與太陽輪和內齒圈的齒數有關。因此，可以在滿足傳動比和裝配條件的情況下，先確定zr和zs，然后按不變位的情況確定zp，再將減少1～2個齒數，若傳動比保持不變，則齒數僅有一個是獨立的，變位系數中僅有兩個是獨立的，此時的設計變量為：

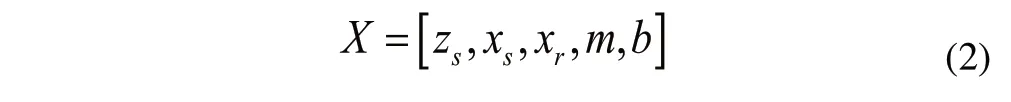
本文研究中試驗設計工況為：輸入轉矩為4354.8N·m，輸入轉速為996.4rpm，功率為454Kw。結合研究對象和研究目的，分別將傳動系統的最大應力和加速度作為試驗的兩個指標；進行試驗時，需指定試驗因素的取值范圍，即可行的試驗空間。對于行星齒輪傳動，將傳動系統齒輪參數的變化范圍作為試驗空間。表1為本次試驗的試驗空間。

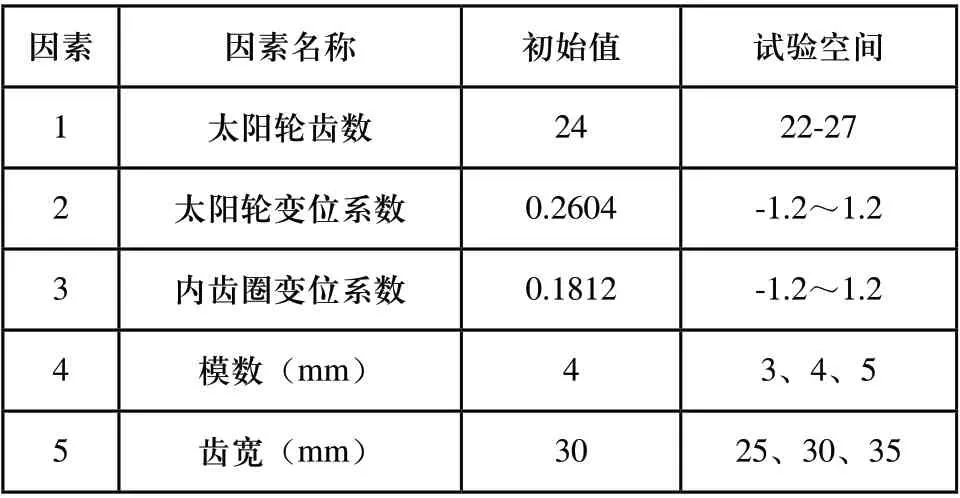
表1 試驗因素及試驗空間

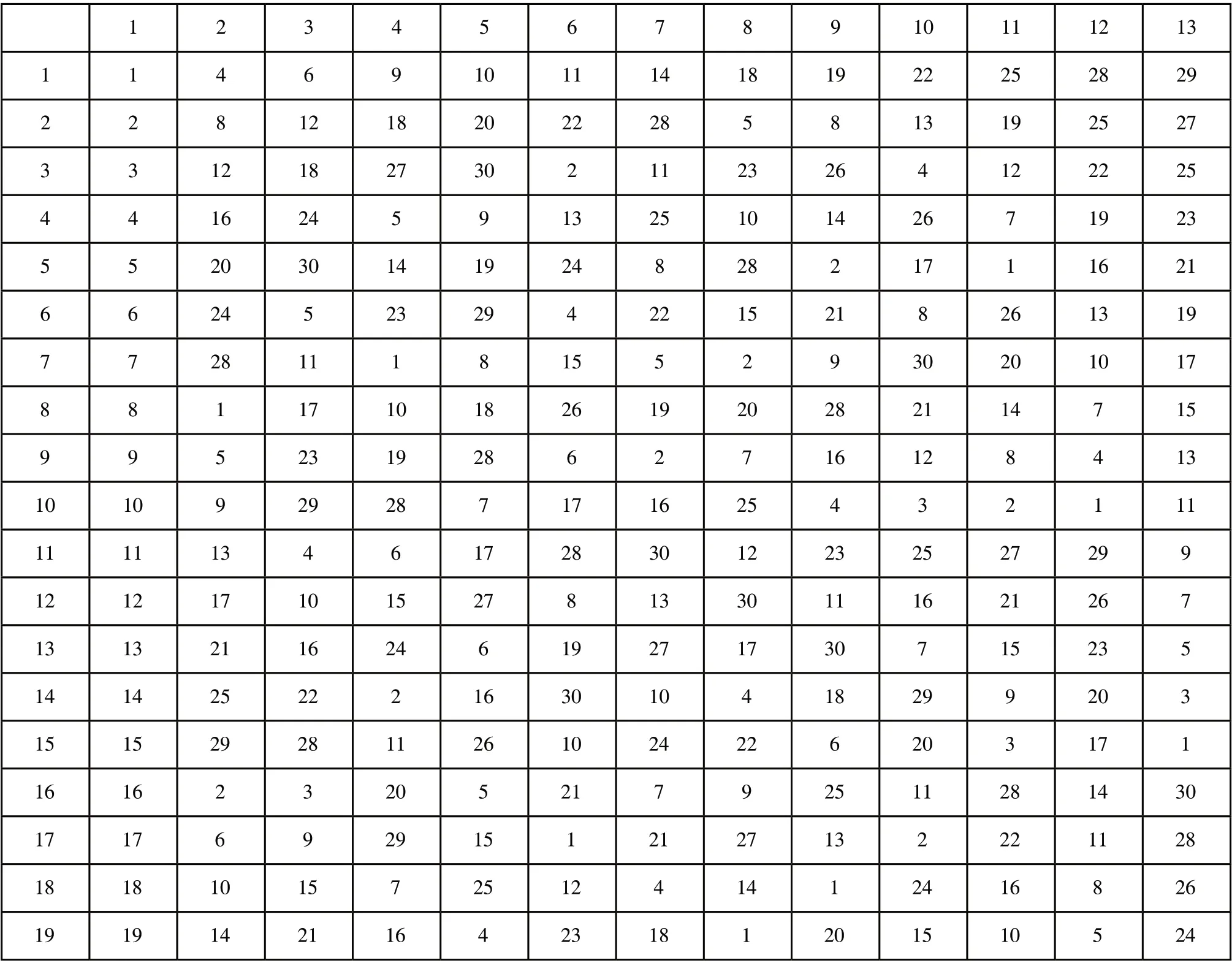
表2 U30×（3013）均勻表及使用表

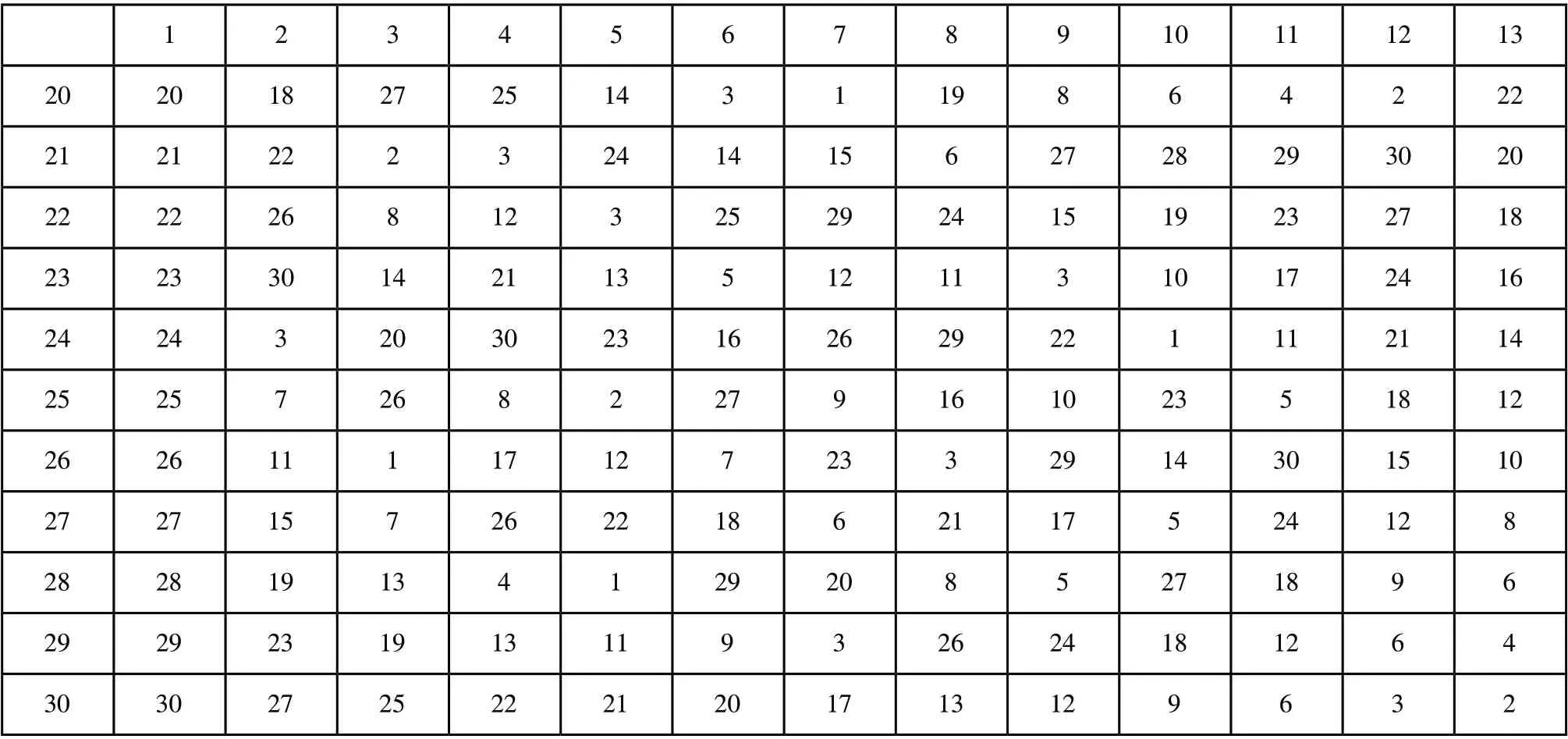
表2（續）

研究中涉及的試驗因素有5個，根據均勻設計表，能安排5因素的試驗方案有很多種。在均勻試驗中，試驗次數可以等于最大水平數，而試驗次數與試驗因數個數有關，一般來說，試驗次數選為試驗因素個數的3倍左右為宜，有利于建模和優化[6]。在本試驗中，考慮到每個因素的取值范圍較大，適當地增加試驗次數有助于保證試驗的精確性及提高響應面精度。

根據表2中的試驗空間可知，本次試驗各試驗因素水平不同，故需采用混合均勻實驗設計表，項目研究中在30水平的均勻表的基礎上，將其變為五因素混合設計表。30水平的均勻設計表有U30×（3013）及其使用表如表2所示[7,8]。五因素試驗的均勻度偏差為0.1465，試驗時應按照均勻設計表中的第1、2、5、7和8列進行試驗設計。

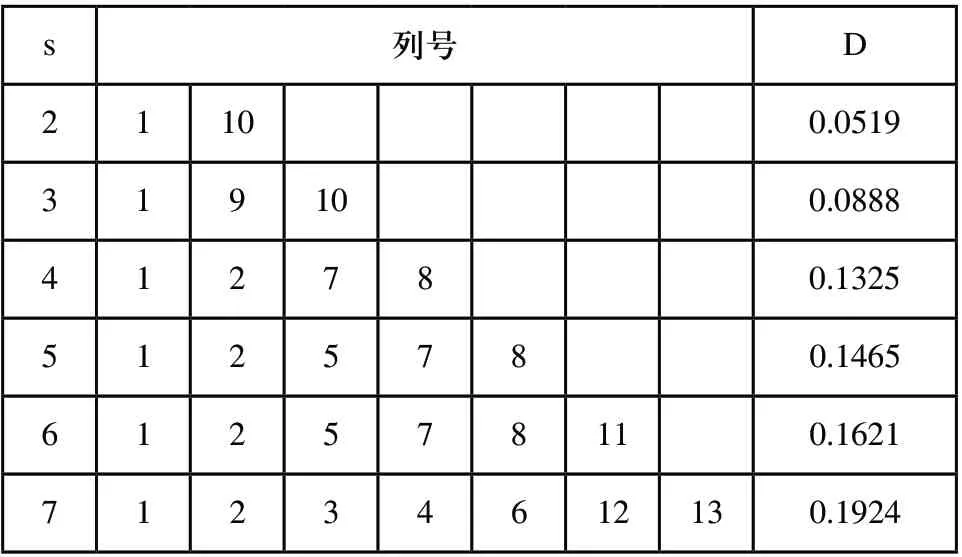
表3 U30×（3013）的使用表

建立的試驗設計方案如表4所示。

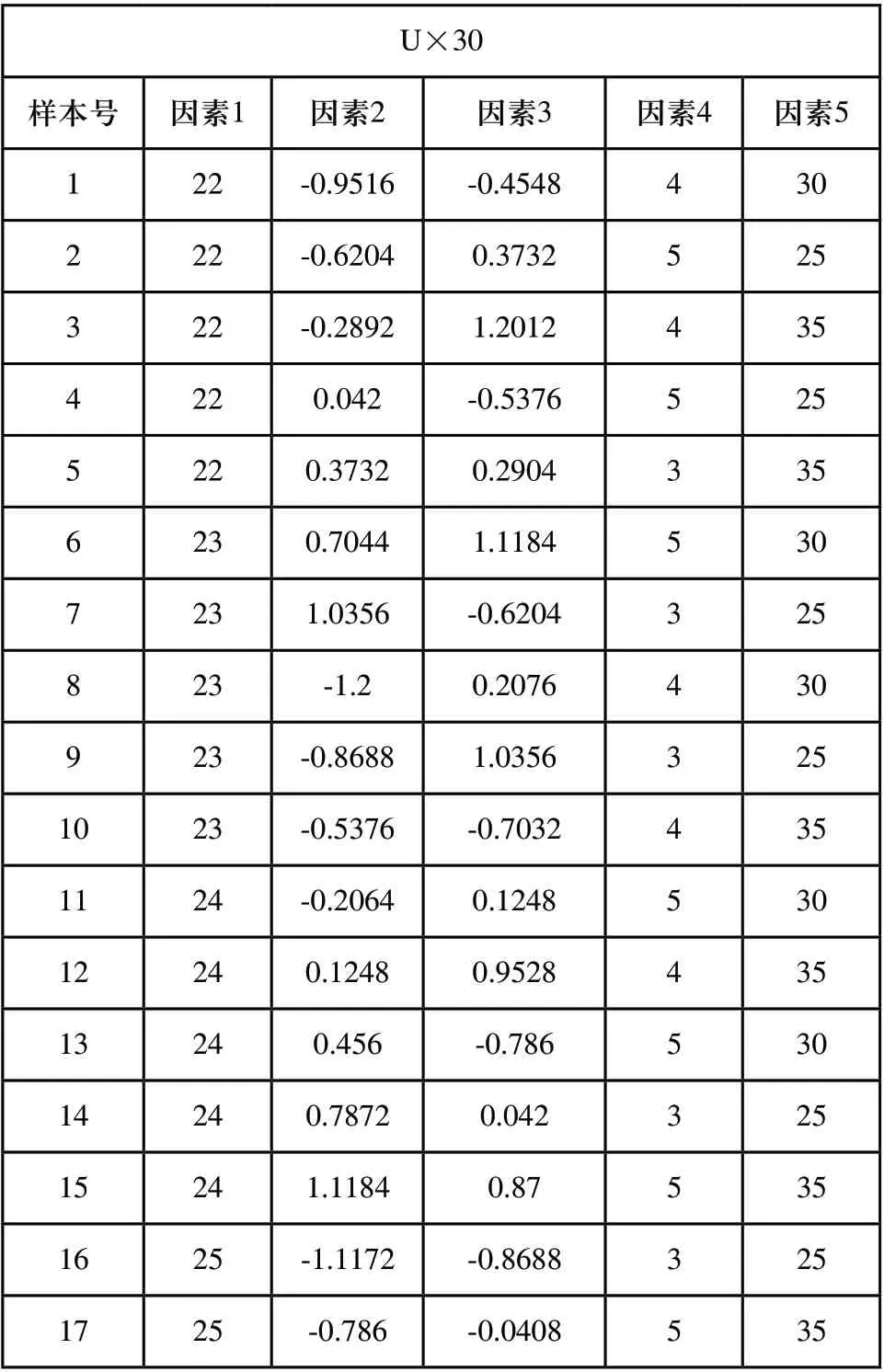
表4 試驗設計方案

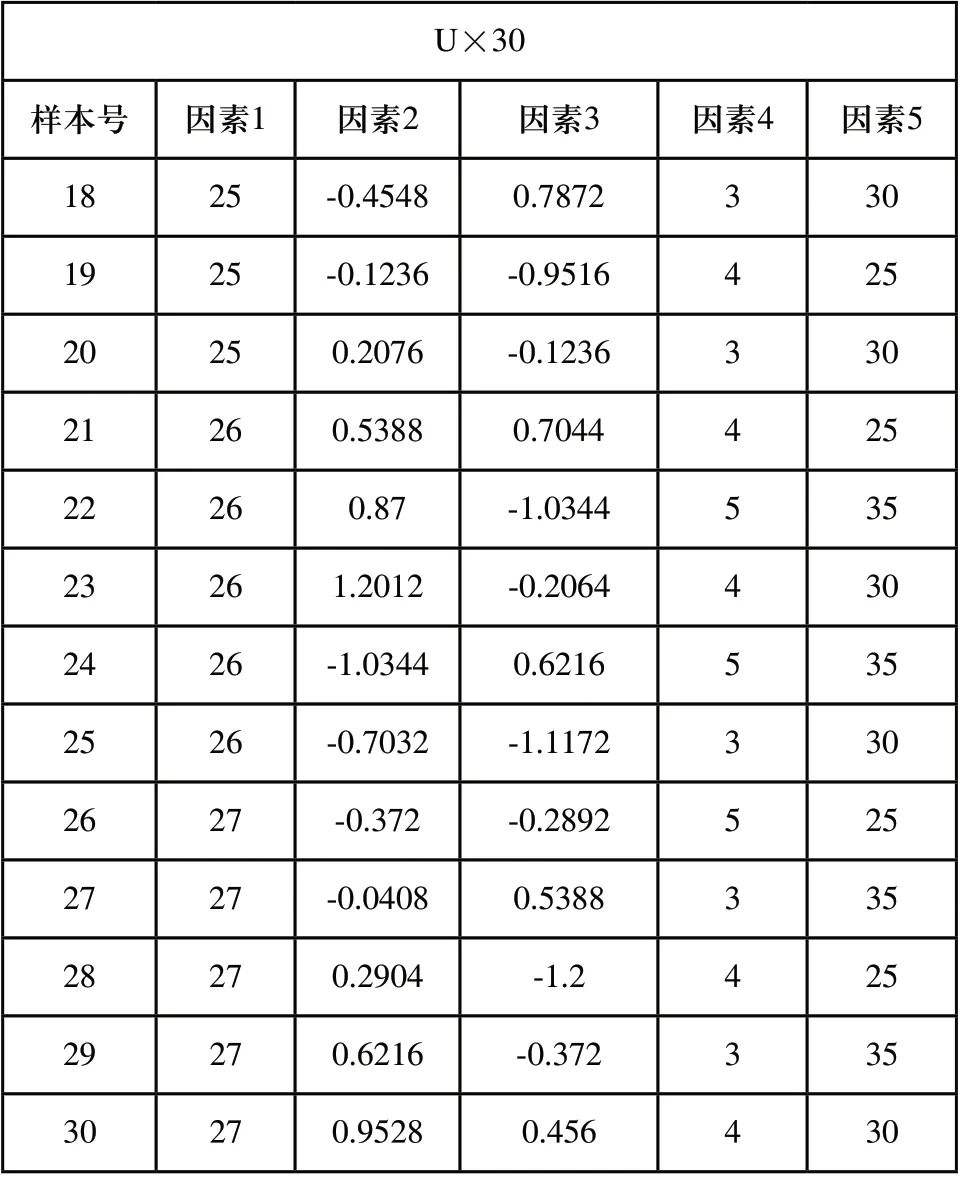
表4（續）

2 響應面模型

對設計變量和動態特性響應采用最小二乘法擬合，得到傳動系統動態特性中表面最大應力Ystr和加速度Ya的二次多項式響應面近似模型，響應面擬合系數如表5和表6所示。

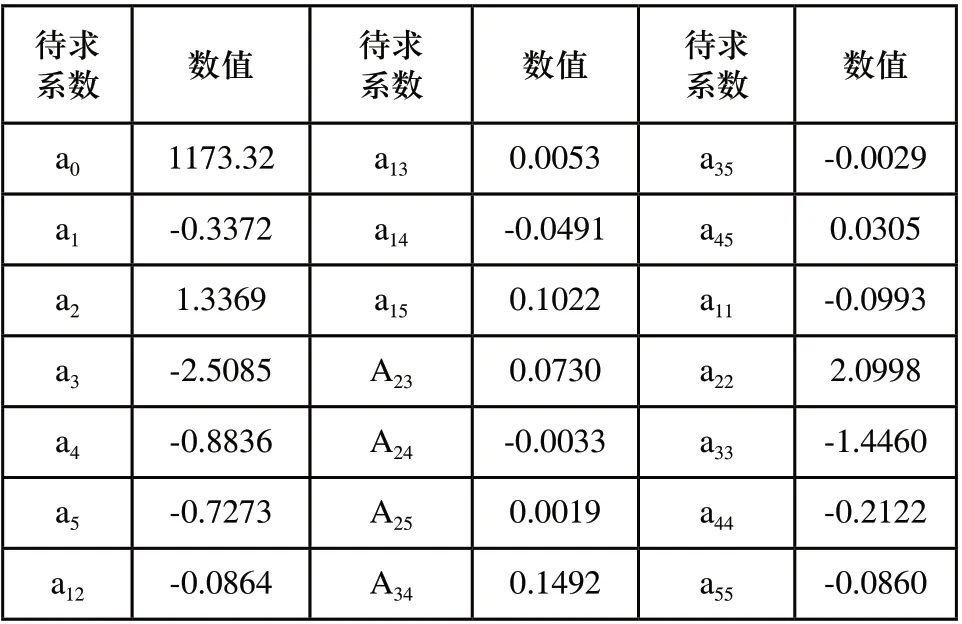
表5 傳動系統表面最大應力響應面擬合系數

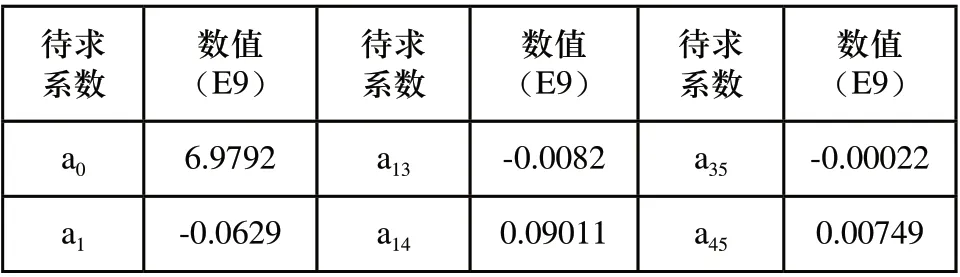
表6 傳動系統表面最大加速度響應面擬合系數

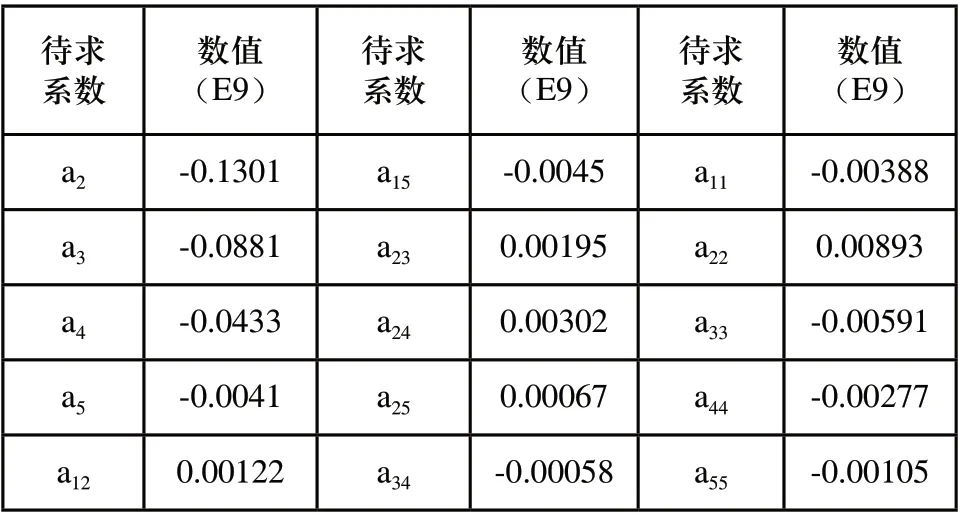
表6（續）

3 近似響應面模型結果分析

1）誤差分析

為了進一步判斷響應面近似模型對真實響應面的逼近程度，需對擬合的二次響應面近似模型進行精確度檢驗。復相關系數R2和修正復相關系數R2adj常作為響應面模型精度的評價指標[9～11]，它們的計算結果如表7所示。兩個響應面近似模型的復相關系數和修正復相關系數都大于0.9，滿足工程精度要求，擬合得到的近似響應面模型精確可靠。

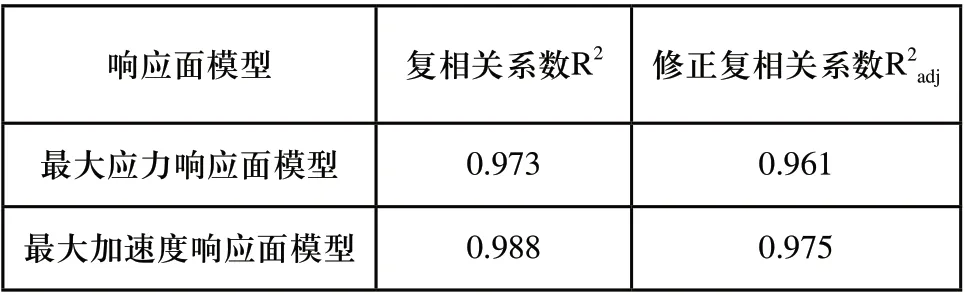
表7 響應面近似模型的復相關系數和修正復相關系數

2）結果分析及討論

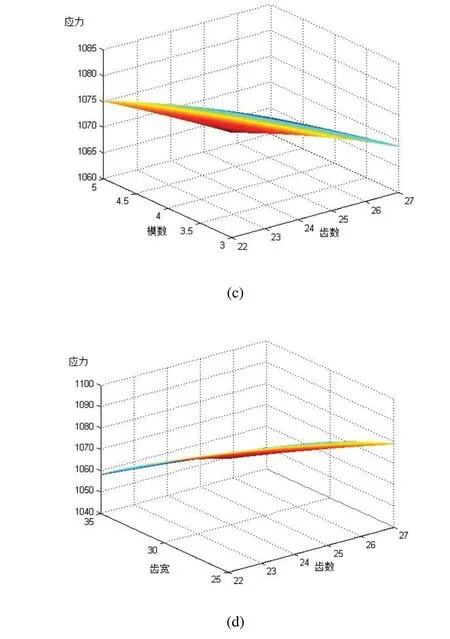
圖2 基于系統應力的二次響應面交互項曲面

如圖2所示，太陽輪齒數和太陽輪變位系數的交互項曲面為一個凸曲面，在一定范圍內，當太陽輪齒數不變時，極限應力隨著內齒圈變位系數的增大先增大后減小；太陽輪齒數和內齒圈變位系數的交互項曲面為一個凹曲面，極限應力隨著太陽輪變位系數的增大先減小后增大；極限應力隨著齒輪模數和齒寬的增大而減小，且模數和齒寬與太陽輪齒數的交互作用對系統應力影響較大。

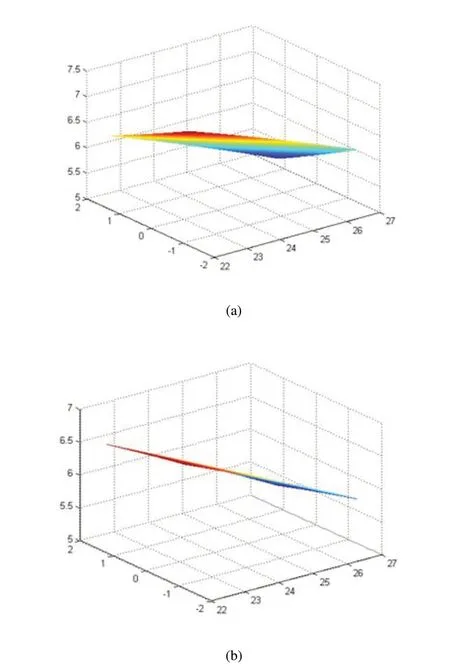
圖3 基于系統加速度的二次響應面交互項曲面

如圖3所示，太陽輪變位系數和內齒圈變位系數不變時，太陽輪齒數在較大值處系統加速度響應較小。模數和太陽輪齒數的交互作用以及齒寬和太陽輪齒數的交互作用對系統加速度響應影響較大，且在二者較大值附近，系統加速度響應最優。

4 結論

建立了減速器傳動系統和箱體表面最大應力和最大加速度的二次多項式響應面近似模型，得到了行星傳動系統特征參數與系統動態特性間的映射關系，得到的主要結論有：

1）當太陽輪齒數不變時，極限應力隨著內齒圈變位系數的增大先增大后減小；太陽輪齒數和內齒圈變位系數的交互項曲面為一個凹曲面，極限應力隨著太陽輪變位系數的增大先減小后增大；極限應力隨著齒輪模數和齒寬的增大而減小，且模數和齒寬與太陽輪齒數的交互作用對系統應力影響較大。

2）太陽輪變位系數和內齒圈變位系數不變時，太陽輪齒數在較大值處系統加速度響應較小。模數和太陽輪齒數的交互作用以及齒寬和太陽輪齒數的交互作用對系統加速度響應影響較大，且在二者較大值附近，系統加速度響應最優。