非調制大容量氣槍信號處理中反褶積方法的對比研究

孫天為 王寶善

摘要：利用云南賓川主動源資料，對比分析了阻尼系數法、水準法、最小二乘法、時間域迭代法以及維納法去除氣槍信號震源響應的效果。結果表明：①在參數選擇正確時，以上方法得到的波形差異不大。其中阻尼系數法、水準法參數選取難度最大，最小二乘法雖然能夠自動找到最優解，但步長設置過小時，計算效率低，步長設置過大時，易出現假極值點。時間域迭代法及維納法的參數對結果的影響相對較小。②對于高信噪比疊加信號，時間域迭代法得到的信號信噪比最高，計算時間對比其他方法增加不大，是一種較好的反褶積方法。對于單槍低信噪比信號，當只需要到時信息時，可使用時間域迭代法，但需波形信息時，從波形的可信度及計算效率上考慮，維納法是更加折中的方法。

關鍵詞：主動源;氣槍震源;非調制大容量氣槍;反褶積

中圖分類號：P315.61文獻標識碼：A文章編號：1000-0666（2019）01-0088-08

0引言

分析地震波是了解地球內部結構、組成、狀態和演化的有效手段（陳颙，朱日祥，2005）。利用人工震源對區域地下結構進行探測是研究地球內部結構及介質特性的一種新型手段。20世紀60年代，氣槍震源開始應用于海洋勘探，至今已取得巨大成就。近年來，中國地震局將海上氣槍主動源引入陸地，建立了包括賓川在內的多個試驗場，開展了大量實驗工作，獲得了豐富的數據。研究發現，大容量氣槍震源與其他勘探手段相比有著激發性能高、可重復性好、綠色環保、安全性高的優點，應用前景廣闊（陳颙等，2007;林建民等，2008;王偉濤等，2017）。

臺站間的格林函數直接攜帶臺站區域的地下結構信息（許立生，陳運泰，1996）。為得到格林函數，需要用反褶積計算去除觀測信號中震源的影響。氣槍激發時氣泡子波的混疊效應使得氣槍的觀測信號相比天然地震信號更為復雜，反褶積后可得到更為清晰的震相（Wangetal，2018;Yangetal，2018），故在處理氣槍信號資料時，反褶積運算十分必要。許多更深入的研究建立在反褶積計算的結果之上，但是實際觀測信號中存在背景噪聲及儀器噪聲，這些噪聲對計算結果的穩定性與真實性有極大的影響。為解決此問題，很多反褶積數學方法被提出（Bell，Sejnowski，1995;Helmberger，Wiggins，1971;Sheehanetal，1995），雖然這些方法的數學模型是確定的，并在一定程度上能消除噪聲的影響，但是模型的參數需要根據數據質量半經驗進行選取，這些參數將直接影響反褶積效果（Lines，Treitel，1984），并且每種方法的處理效率及適用的信號也不同。因此，為不同質量的氣槍信號選取較為合適的反褶積方法及參數十分重要。為對比不同方法的運算效果及處理效率，本文將頻率域內的阻尼系數法、水準因子法、最小二乘法、時間域迭代法及維納法應用于云南賓川氣槍主動源資料對比不同方法的計算效果。

1反褶積方法原理

地震波的觀測信號d（t）可表示為：

式中：是卷積符號;s（t）為震源時間函數;g（t）為格林函數;i（t）為臺站儀器內部對信號的脈沖響應;n（t）為觀測信號的周圍噪聲。

圖1為式（1）所表達的線性系統，該系統由2個褶積模塊和1個疊加模塊組成。系統輸入震源時間函數s（t），輸出觀測信號d（t）。

在實際的數據處理中忽略周圍噪聲影響，并去除儀器響應，可得：

求解格林函數轉化為s（t）的反褶積，在氣槍信號處理過程中，s（t）可由震中距較小的參考臺接收到的信號近似代替。

一般來說，2個信號在時間域中的褶積等于這2個信號在頻率域中的乘積：

故頻率域的反褶積可直接轉化為除法，但地震波信號通常具有高頻截止性，而噪聲信號通常又是高頻的，在兩者相除時震源時間函數中的高頻噪聲會被放大，造成解的不穩定性（Gurrolaetal，1995）。為改善解的這一問題，一些反褶積算法被提出。

1.1阻尼系數法

阻尼系數法假設噪聲全部為具有零均值的高斯隨機噪聲。調整后的反褶積表達式為：

式中：*代表復共軛;δ為阻尼系數。

數學上，阻尼系數的加入相當于在分母中加入一個不為零的常數，減小了分母接近零時的影響，提高解的穩定性。物理上，阻尼系數在分母項的能量譜密度中加入了白噪聲（圖2a），大幅度提高了低頻部分信號功率，故而減小了高頻噪聲對計算結果的影響。阻尼系數的引入本質上相當于加入了一個低通濾波器。當阻尼系數等于零時，式（5）退化為直接求頻率域反褶積公式（4）。阻尼系數的大小通常根據信號的噪聲水平及功率譜密度峰值半經驗的選取，當阻尼系數的值選擇過小時，穩定效果不明顯;數值過大時，分母將趨于常數，所以參數的選擇十分重要。

式中：c為水準比例因子。

阻尼系數法將分母能量譜密度中每一個頻率的振幅都加了一個常數，而水準法是選定一個閾值，這個閾值由水準比例因子c乘以能量譜密度的峰值所確定，當分母的能量譜密度的振幅超過水準閾值時保持不變，低于閾值時提升到水準閾值（Menke，1984）（圖2b）。水準法也相當于對分母的能量密度譜做了一個低通濾波，通過向低于水準閾值的部分加入白噪聲而提升了分母能量譜密度的帶寬。水準比例因子的大小同樣需要半經驗的選取，當水準比例因子過大時分母將趨于常數。

1.3最小二乘法

最小二乘法由Bostock（1998）提出，原理與阻尼系數法相同，只是阻尼系數δ無需自行選擇。使交叉驗證函數（GCV）值最小的δ值即為最佳的阻尼系數。GCV函數定義如下：

式中：N為在對原信號進行傅里葉變換時的頻率采樣點的個數;ωn為對應的頻率;M為地震信號的個數。

式（7）分子為預測信號與實際觀測信號的殘差平方和（RSS）用來評估預測值與實際值的吻合程度。分母中的M，N用來衡量模型的自由度，X用來衡量阻尼因子δ的引入對原始模型的改變。

GCV是一種從回歸分析中引入的正則化方法。選定初始δ和迭代步長后，反復迭代求得GVC函數，并找出使GCV函數最小的δ值，即最佳的δ值。最后將最佳的δ值帶回式（5）求得最終反褶積結果。

初始假設同樣是認為數據中的噪聲為白噪聲，但對噪聲的能量及振幅的分布沒有特別的假設（Bostock，1998）。

1.4時間域迭代法

時間域迭代法依賴互相關函數，并通過迭代構造格林函數（Kiknchi，Kanamori，1982）。具體方法步驟為：

①通過互相關掃描式（9），求得u（t）與s（t）互相關函數（rsu）平方最大時所對應的時間延遲t1：

②通過式（11）和（12）求得幅值m1，預測信號可表示為式（13）：

③用原始信號u（t）減去預測信號u1pre（t）得到新的觀測信號u1（t），迭代步驟①，②，直至原始信號與預測信號的殘差平方和不再大于某個閾值。

原始信號和格林函數可以分別表示為：

最后利用帶通濾波去除高頻噪聲的影響。

1.5時間域維納法

在時間域內可以將觀測信號看成格林函數與震源時間函數的褶積，將格林函數視為濾波器的脈沖響應，將震源時間函數和觀測信號分別看做濾波器的輸入和輸出。但事實上無法得到這樣的濾波器，只能得到它的近似估計：

假設s（t）的激勵下濾波器的實際輸出u～（t），與期望輸出u（t）盡可能相似，取誤差平方和最小，即：

對式（17）求極小，可得如下矩陣方程：

式中：gτ為待定格林函數的時間序列;aτ為震源時間函數的自相關;cτ為震源時間函數與觀測信號的互相關。對該方程求解即得到格林函數（吳慶舉等，2003）。

2處理流程

2.1數據選擇

云南賓川地震信號發射實驗臺位于紅河斷裂與程海斷裂之間，坐落于大銀甸水庫，由4支容量為2000in3的氣槍組成，每次激發相當于ML0.7地震。氣槍放置深度為10m，自2012年9月建成后，每周激發20次，2014年9月后每周激發60次（陳佳等，2017）。接收系統儀器由Reftek130數據采集器和頻帶范圍為2s～100Hz的短周期GuralpCMG-40T地震計組成。本文選用2014年震中距為17km的53258臺（圖3a）的資料。此臺從未發生過替換，數據連續率為91%，工作穩定（張云鵬等，2017）。參考臺的選用頻帶范圍為2s～100Hz，距信號發射臺40m的CKT1臺。因先疊加后反褶積的處理流程的結果在信噪比、計算效率等方面優于先反褶積后疊加（翟秋實等，2016），故在反褶積前使用RMS線性疊加方法（蔣生淼等，2017）共疊加1092條Z分量數據，以提高信噪比（圖3b，c）。

2.2數據處理流程

為提高信號信噪比，在對觀測數據做反褶積前后，需要進行濾波及信號疊加，操作流程如下：

①去均值，去線性趨勢。

②帶通濾波：氣槍源的優勢頻帶為3～7Hz（楊微等，2013），在進行反褶積前進行2～8Hz的帶通濾波。

③信號疊加：對于氣槍源，RMS篩選疊加能有效提高噪聲地震記錄和小地震信號事件（蔣生淼等，2017）。使用RMS線性疊加方法對53258臺的信號進行疊加，提高信噪比。

④使用不同方法進行反褶積。

⑤帶通濾波：因為反褶積穩定性較差，在反褶積之后還需要進行帶通濾波，本次帶通濾波頻帶設置為2.5～5Hz。

3計算結果

經過不斷調整參數，最終得到5種反褶積方法最佳的格林函數，如圖4所示。使用阻尼系數法時選取阻尼系數為1010;使用水準法時選取水準比例因子為10-4;用最小二乘法時，使交叉對比函數最小對應的阻尼系數值為1.78×1010;使用時間域迭代法時，設定迭代次數為2000次或數據殘差小于0.005時終止迭代。

為了驗證所得格林函數的穩定性，計算了格林函數與參考信號褶積所得的信號和原觀測信號的互相關系數，對應于圖4右側數字。從圖中可以發現，當觀測信號信噪比較高且反褶積的參數設置正確時，每種方法計算得到的相關系數都在0.9以上，其中最小二乘法求得的互相關系數最高。同時所有方法都能使S震相變得更加清晰，減小了原始信號受到氣槍激發時氣泡子波混疊的影響。為進一步對比各種方法的區別，研究了各種方法參數的影響、計算效率及信噪比。

4討論

4.1參數影響

由圖4可知，在疊加信號信噪比較高且參數選取正確時，各反褶積方法的計算結果十分相近。鑒于參數的選擇難度以及當參數選取不正確時對反褶積結果的影響不同，故對參數的影響做進一步討論。

（1）阻尼系數法：阻尼系數在震源子波的能量譜密度中加入白噪聲，降低解的不穩定性。從圖5可以看出，隨著阻尼系數的變大，震源時間函數功率譜密度的峰值會被迅速提高，造成格林函數振幅被迅速縮小。

（2）水準法：在頻率域反褶積時，水準比例因子的選取是一個難點，該因子越大反褶積結果越穩定，但失真度也越大。因此需要根據數據質量多次嘗試選擇水準比例因子（翟秋實等，2016）。水準法不改變震源時間函數的能量譜密度峰值，不會出現格林函數振幅嚴重衰減的情況，如圖6所示。從圖5，6可見，阻尼系數法參數的變化對計算結果的影響顯著，而水準法得到的結果更加穩定。

（3）最小二乘法：該方法是一種通過試解自動尋找最佳阻尼系數的方法。實際應用中發現，阻尼系數的量級一般在1010左右，試解運算時，步長設置過大易出現錯誤的極點，步長過小計算量大、效率低，但阻尼因子系數的取值更加精準。

（4）時間域迭代法：由于時間域迭代反褶積此方法是將格林函數近似的看作由一些平移縮放的δ函數組成，勢必會引入其他頻帶的噪聲，故反褶積后的帶通濾波頻帶的選擇十分重要。頻帶選擇不當將出現波形信號變形。從圖7中可以看出當濾波頻帶選為3～8Hz時，出現大量高頻噪聲。但對于氣槍源優勢頻帶較窄，其處理效果較好。

（5）時間域維納法：該方法與最小二乘法原理相近，都是以最小均方誤差作為輸出準則，但最小二乘法是在頻率域內求解，而維納法是在時間域求解。在求解矩陣方程時由于構造的托普利斯矩陣為病態矩陣，解是不穩定的，需要加入白噪聲，本文研究預白百分比為0.01%。加入白噪聲后矩陣的條件數由108降到105。

4.2信噪比及計算效率

信噪比是衡量信號質量的重要標準，本文對比了不同反褶積方法得到的格林函數的振幅信噪比，并計算了反褶積計算所需的時間以衡量各方法的計算效率，如表1所示。其中選取P波到時前2s為背景噪聲時窗，P波到時后7s為信號時窗。

從表1中可以發現，時間域反褶積得到的信號信噪比最高，這是因為時間域反褶積通過互相關掃描拾取振幅最大的位置近似為狄拉克函數，能夠有效壓制小振幅的背景噪聲，將低于閾值的信號直接置0。從計算效率上講，雖然最小二乘法及時間域迭代法都需要進行迭代，但時間域迭代法的計算時間遠遠小于最小二乘法。

4.3低信噪比信號運算

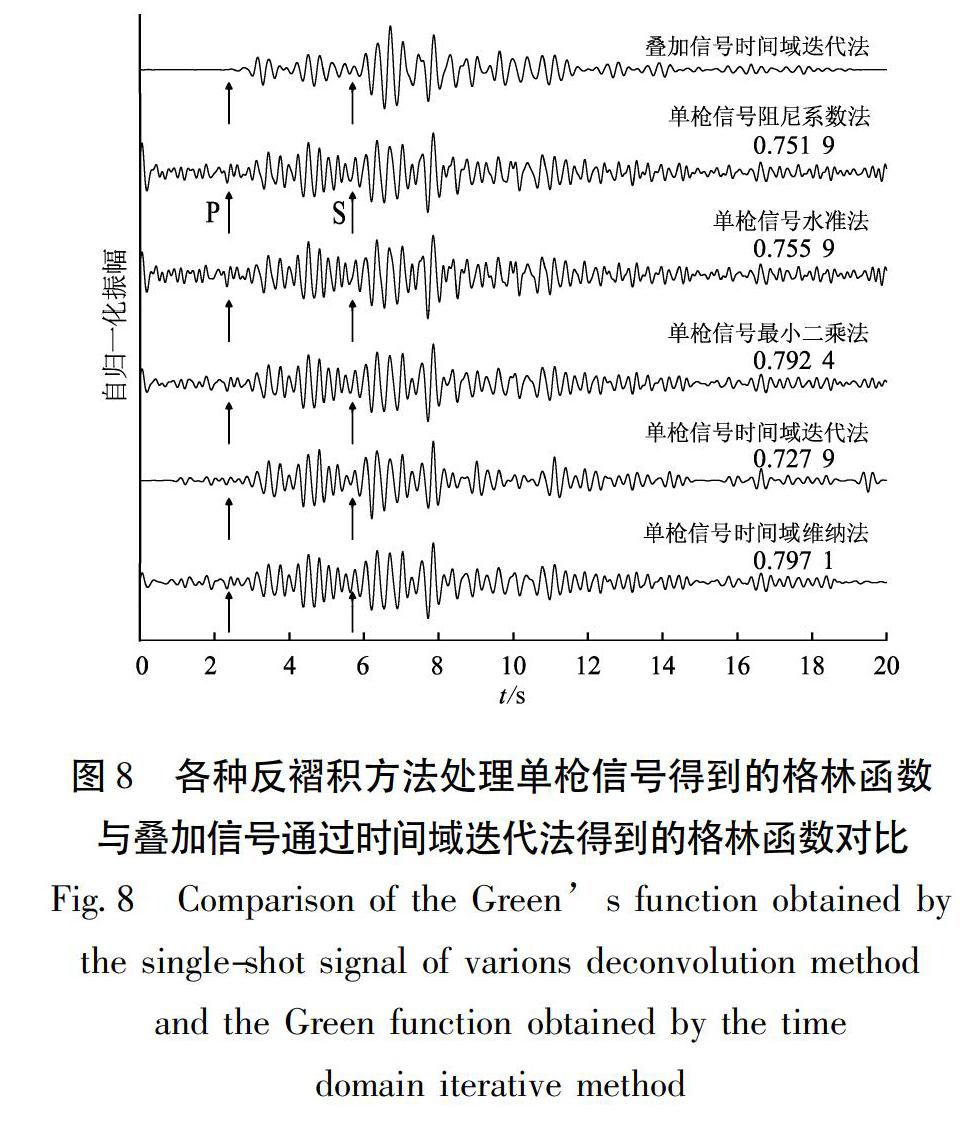
上述方法均使用在經過疊加的高信噪比信號上，而低信噪比信號的運算效果也是衡量反褶積算法穩定性的標準。本文使用不同反褶積方法對具有較低信噪比的單次激發信號的計算效果進行比較。選擇2014年1月2日17時整激發的氣槍信號，處理結果如圖8所示。從圖中可以看出，相對于頻率域，時間域的反褶積方法得到的格林函數有著更好的信噪比，能夠更好地識別P波、S波到時。且時間域迭代法比維納法信噪比更高，但各個方法得到的單次激發格林函數相比疊加信號的格林函數波形都有所變形。為量化各個方法得到波形的變形情況，圖8右側數字表示單槍信號格林

函數與疊加信號格林函數的相關系數，最小二乘法和時間域維納法得到的格林函數波形變形較小，時間域迭代法得到的格林函數雖然信噪比較高，但波形變形最嚴重。

5結論

本文利用云南賓川主動源資料，對比分析了阻尼系數法、水準法、最小二乘法、時間域迭代法以及維納法去除氣槍信號震源響應的效果，得到如下結論：（1）阻尼系數法和水準法需要通過試錯法找出最優解，參數選取難度最大;最小二乘法能夠自動化找到最優解，但迭代步長設置過小時迭代次數過多，步長設置過大時，易出現假極值點，步長的選取仍然需要通過信號的質量半經驗的選取，整體計算效率不高。相比前3種方法，時間域迭代法及維納法處理氣槍信號時的參數較為固定，對波形的影響相對較小。（2）對于高信噪比的疊加信號，時間域迭代法得到的信噪比最高，相比天然地震信號氣槍信號主頻帶寬較窄且十分固定，反褶積后的窄帶濾波能有效改善算法引入高頻噪聲的缺點，相比在天然地震中的應用，其在氣槍信號中的應用更有優勢，是一種較好的計算方法。對于單次激發信噪比較低的信號計算結果相對復雜，時間域迭代法得到格林函數信噪比最高，且P，S震相較為清晰，但是波形變形也最為嚴重，故建議在只需要信號震相到時信息時可以使用時間域迭代法。需波形信息時，最小二乘法和維納法都可以得到可信度較高的波形，但從計算效率上考慮，維納法是更加折中的方法。

參考文獻：

陳佳，葉泵，高瓊，等.2017.利用氣槍震源信號研究2016年云龍MS5.0地震前后波速變化特征[J].地震研究，40（4）：550-556.

陳颙，張先康，丘學林，等.2007.陸地人工激發地震波的一種新方法[J].科學通報，52（1）：1-5.

陳颙，朱日祥.2005.設立“地下明燈研究計劃”的建議[J].地球科學進展，20（5）：485-489.

蔣生淼，王寶善，張云鵬，等.2017.一種基于信號噪聲特征的主動源數據自動篩選與疊加方法[J].地震研究，40（4）：534-542

林建民，王寶善，葛洪魁.2008.大容量氣槍震源特性及地震波傳播的震相分析[J].地球物理學報，53（2）：342-349.

王偉濤，王寶善，蔣生淼，等.2017.利用氣槍震源探測大陸淺部的地震學研究回顧與展望[J].地震研究，40（4）：514-524.

吳慶舉，田小波，張乃鈴，等.2003.用Wiener濾波方法提取臺站接收函數[J].中國地震，19（1）：41-47.

許立生，陳運泰.1996.用經驗格林函數方法從長周期數字波形資料中提取共和地震的震源時間函數[J].地震學報，18（2）：156-169.

楊微，王寶善，葛洪魁，等.2013.大容量氣槍震源主動探測技術系統及試驗研究[J]，中國地震，29（4）：399-410.

翟秋實，姚華建，王寶善.2016.氣槍震源資料反褶積方法與處理流程研究[J].中國地震，32（2）：295-304.

張云鵬，李孝賓，王偉濤，等.2017.云南賓川地震信號發射臺的流動觀測數據服務系統及數據質量評估[J].地震研究，40（4）：525-533.

Abstract

UsingairgundatafromBinchuaninYunnanProvince，wecomparethecalculationeffectsofdampingfactormethod，waterlevelmethod，leastsquaresmethod，timedomainiterationmethodandWienermethodontheremovalofthetimefunction.Theresultsshowthat：①Thewaveformsobtainedbytheabovemethodshavelittledifferencewhentheparametersarecorrectlyselected.Thedampingcoefficientmethodandwaterlevelingmethodarethemostdifficulttochoose.Theleastsquaresdeconvolutioncanautomaticallyfindtheoptimalsolution，butthecalculationefficiencyistoolowifthestepsizeissettoosmall，andfalseextremepointsarelikelyoccurredwhenthestepsizeissettoolarge.TheparametersofthetimedomainiterationandWienermethodhaverelativelylittleinfluenceontheresults.②Forhighsignal-to-noiseratio（SNR）stackedsignals，theSNRobtainedbythetimedomainiterativedeconvolutionmethodisthehighest，andthecomputationtimeiswithintheacceptedrange，soitisagooddeconvolutionmethod.Forsingle-gunlowSNRsignals，thetimedomainiterativemethodcanbechosenwhenwejustneedtopickthearrivaltime.Butwhenwaveforminformationisneeded，theWienermethodismoreeffectiveintermsofthereliabilityofthewaveformandthecalculationefficiency.

Keywords：activeseismicsource;airgunseismicsource;untunedlargevolumeairgun;deconvolution