LNG廠站安全閥背壓和天然氣放散管道計算
李建勛, 邢少郡
(1.中國市政工程華北設計研究總院有限公司,天津300381;2.吉林市大地技術咨詢有限公司,吉林吉林132000)
1 問題的提出
在LNG氣化站設計中,當進行LNG儲罐安全閥選型計算時,一些設計人員將安全閥的背壓取某個確定的值,未與天然氣放散管道聯系起來。實際上,安全閥的背壓等于天然氣放散管道的起點壓力。該起點壓力取決于放散量、天然氣組成、安全閥前天然氣的壓力和溫度、環境溫度、放散管道各管段的長度和管徑等許多因素,參數之間的關系比較復雜。因此,有必要對天然氣放散管道計算進行研究。
經過對實例LNG氣化站適當簡化,將EAG加熱器視為一段管段,得到天然氣放散管道的物理模型,見圖1。放散管道共有6個節點,5個管段。圖1中圓圈內的編號為節點編號,管段上的編號為管段編號。節點6是儲罐安全閥的出口,節點1通向大氣。
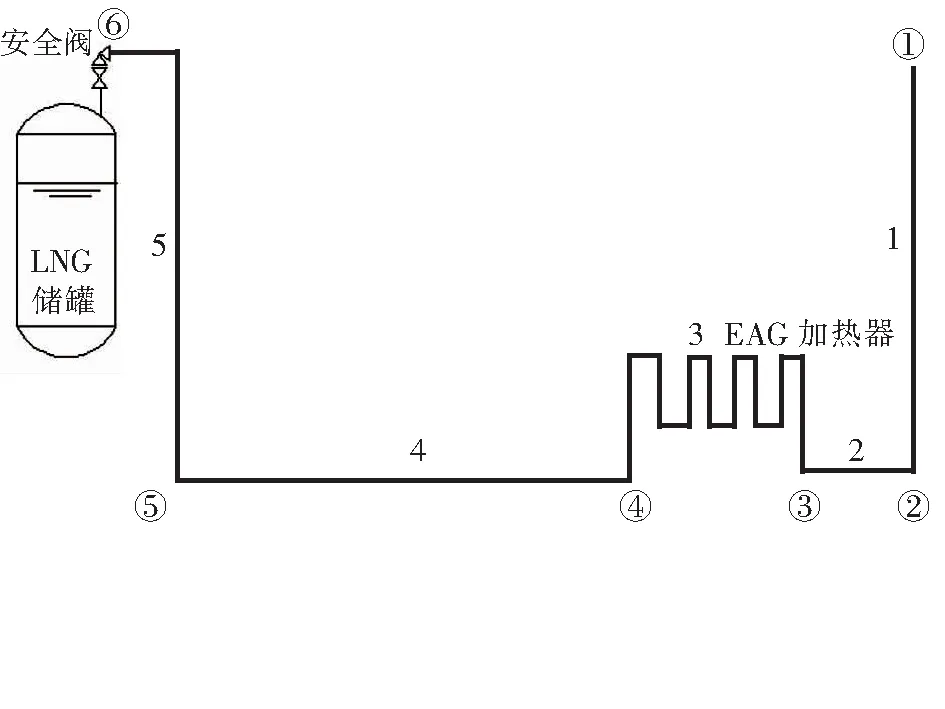
圖1 天然氣放散管道的物理模型
2 放散管道的數學模型
2.1 放散管道中天然氣的流動過程
LNG儲罐發生火災時,LNG迅速氣化,LNG儲罐內氣相空間天然氣壓力迅速升高。當天然氣壓力達到安全閥整定壓力時,安全閥開啟;當天然氣壓力達到安全閥排放壓力時,安全閥全開[1]。天然氣流經安全閥是一個節流過程,安全閥前后天然氣的比焓相等。天然氣流入放散管道后,吸收環境的熱量,溫度逐步升高。由于存在沿程摩擦阻力和局部阻力,壓力逐步降低。在放散管道出口,天然氣排入大氣。
2.2 已知參數和待求參數
① 已知參數
天然氣的組成。始端節點的質量流量、比焓。環境溫度。各管段的傳熱系數。各管段的內直徑、外直徑、長度、局部阻力系數。
② 待求參數
各節點的壓力、溫度。
③ 判斷參數
a.考慮到放散天然氣溫度較低,在參考GB 50028—2006《城鎮燃氣設計規范》相關條文基礎上,對末端節點,出口密度與環境空氣密度的比值應小于等于0.85。
b.始端節點的壓力(按表壓計),應小于排放壓力的10%。
2.3 各管段的流量關系
低溫天然氣從節點6流入,從節點1流出,中間節點無天然氣流入或流出,因此管段1~5的質量流量是相同的。
2.4 各管段的壓力關系
對于第i管段,為簡化計算,天然氣的溫度取該管段起點溫度和終點溫度的平均值。基于有關文獻[2]425,采用質量流量,起點和終點的壓力關系為:
(Ts,i+Te,i)
(1)
式中ps,i——第i管段起點天然氣絕對壓力,Pa
pe,i——第i管段終點天然氣絕對壓力,Pa
λi——第i管段的摩擦阻力系數
qm——各管段天然氣質量流量,kg/s
di——第i管段的內直徑,m
ρ0——標準狀態下天然氣的密度,kg/m3
p0——標準狀態下的大氣壓力(絕對壓力),Pa,取101 325 Pa
T0——標準狀態下的溫度,K,取273.15 K
Li——第i管段的長度,m
ζi——第i管段的局部阻力系數
Ts,i——第i管段起點天然氣溫度,K
Te,i——第i管段終點天然氣溫度,K
令:
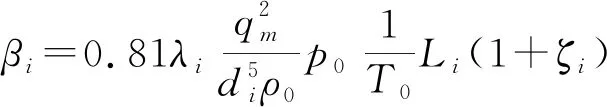
式中βi——系數
將式(2)代入式(1)得:
將1~5管段的壓力關系分別記為f1~f5。以管段4為例,f4為:
式中p5——節點5的天然氣絕對壓力,Pa
p4——節點4的天然氣絕對壓力,Pa
T5——節點5的天然氣溫度,K
T4——節點4的天然氣溫度,K
2.5 各管段的溫度關系
由于放散管道壓力低,不考慮節流效應。
將管段i分成若干個微元管段。由于從環境吸熱,微元管段存在關系[1]:
qmcpdT=πKiDidx(Tsur-T)
(5)
式中cp——天然氣比定壓熱容,J/(kg·K)
T——天然氣溫度,K
Ki——第i管段的傳熱系數,W/(m2·K)
Di——第i管段的外直徑,m
x——與該管段起點的距離,m
Tsur——環境溫度,K
經過積分運算,得到[1]:
Te,i=Tsur+(Ts,i-Tsur)e-αiLi
(6)
式(6)整理得:
e-αiLiTs,i-Te,i+Tsur-e-αiLiTsur=0
(8)
將1~5管段的起點、終點的溫度關系分別記為f6~f10。以管段4為例,f9為:
e-α4L4T5-T4+Tsur-e-α4L4Tsur=0
(9)
2.6 邊界條件
① 始端節點的比焓關系
始端節點,即節點6,是安全閥的出口。安全閥閥前的壓力、溫度可由相平衡計算得到,即比焓已知。安全閥放散前后,天然氣的比焓相等。將始端節點的比焓關系記為f11,即:
h6-hval=0
(10)
式中h6——節點6的天然氣比焓,kJ/kg
hval——儲罐處安全閥進口天然氣比焓,kJ/kg
② 末端節點的壓力關系
末端節點,即節點1,與大氣相通。將末端節點的壓力關系記為f12,即:
p1-pa=0
(11)
式中p1——節點1天然氣絕對壓力,Pa
pa——大氣壓力(絕對壓力),Pa,取101 325 Pa
3 數學模型的求解
3.1 封閉性分析
氣體狀態方程采用BWRS方程,因此,變量為節點1~6的密度、溫度,12個。管段的壓力關系有5個方程,管段的溫度關系有5個方程,始端節點的比焓關系有1個方程,末端節點的壓力關系有1個方程,共12個方程。方程數量與變量數量相等,滿足封閉性要求。
3.2 BWRS方程壓力和比焓的計算
3.2.1 BWRS方程計算
① BWRS方程的形式為[3]:
式中p——天然氣絕對壓力,kPa
ρm——天然氣體積物質的量,kmol/m3
R——摩爾氣體常數,kJ/(kmol·K),取8.314 kJ/(kmol·K)
A0、B0、C0、D0、E0、a、b、c、d、α、γ——參數
式(12)變形為:
② 利用式(12)計算p對ρm的偏導數,利用式(13)計算p對T的偏導數。
③ 天然氣密度計算:
ρ=ρmM
(14)
式中ρ——天然氣密度,kg/m3
M——天然氣的摩爾質量,kg/kmol
3.2.2 比焓計算
比焓計算式為[2]:
式中h——天然氣(作為實際氣體)的比焓,kJ/kg
h0——天然氣(作為理想氣體)的比焓,kJ/kg
ΔHm——摩爾焓的差,kJ/kmol
①h0的計算式為[2]59-60:
h0=A+BT+CT2+DT3+ET4+FT5
(16)
式中A、B、C、D、E、F——計算h0的參數
A按下式計算:
式中wi——i組分的質量分數
Ah,i——i組分的常數
同理,可計算出B、C、D、E、F常數。
②h0對T的偏導數為:
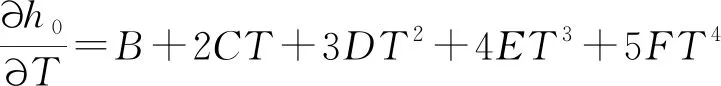
③ ΔHm計算式為[3]:
式(19)變形為:
④ 利用式(19)計算ΔHm對ρm的偏導數,利用式(20)計算ΔHm對T的偏導數。
3.3 求解方法
對由上述12個方程構成的方程組,采用牛頓-拉弗森方法求解,其中構建雅克比矩陣是主要步驟。管段的壓力關系f1~f5、管段的溫度關系f6~f10、始端節點的比焓關系f11、末端節點的壓力關系f12,對節點1~6的密度ρ1~ρ6、節點1~6的溫度T1~T6的偏導數是雅克比矩陣的元素。
① 管段壓力關系的偏導數
以管段4為例,將管段壓力關系f4用密度、溫度的函數表示:
[p(ρm,5,T5)]2-[p(ρm,4,T4)]2-
β4(T5+T4)=0
(21)
偏導數為:

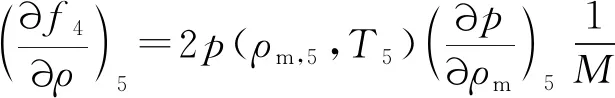

② 管段溫度關系的偏導數
以管段4為例,管段溫度關系f9對溫度求偏導數:
③ 始端節點比焓關系的偏導數
始端節點比焓關系f11用密度、溫度的函數表示:
h(ρ6,T6)-hval=0
(28)
偏導數為:
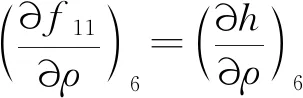
④ 末端節點壓力關系的偏導數
末端節點壓力關系f12用密度、溫度的函數表示:
p(ρm,1,T1)-pa=0
(31)
偏導數為:
3.4 初始密度、初始溫度的確定
設定始端節點(節點6)的絕對壓力為0.11 MPa,依據始端節點的比焓關系,計算得到節點6的初始溫度。根據管段的溫度關系,順著天然氣的流動方向,依次計算得到節點5~1的初始溫度。
根據管段的壓力關系,從末端節點(節點1)開始,逆著天然氣的流動方向,得到節點2~6的初始壓力。當然,計算得到的節點6的初始絕對壓力一般不會恰好是0.11 MPa。根據各節點的初始壓力、初始溫度,利用BWRS方程,得到各節點的初始密度。
4 算例
4.1 計算條件
始端節點天然氣CH4、C2H6、N2的體積分數分別為:73.46%、0.06%、26.48%。天然氣的質量流量為120 kg/h,其比焓與絕對壓力0.66 MPa、135.77 K下的比焓相等。
從安全閥出口到放散塔處的放散管道架空敷設,不進行保冷。室外大氣壓力取101.325 kPa,室外環境空氣溫度取-9 ℃,管內天然氣與環境空氣的傳熱系數取8.141 W/(m2·K)[2]642。管道布置見圖1。EAG加熱器可簡化為由內部并聯帶翅片的4根管道組成,內直徑21 mm,外直徑28 mm,每根管道長度為15 m,局部阻力系數取0.1,其當量傳熱系數取40 W/(m2·K)。
從安全閥出口到EAG加熱器進口的天然氣管道,即管段5和管段4,內直徑均為38 mm,外直徑均為45 mm,局部阻力系數均取0.1,管段5長度為22 m,管段4長度為50 m。EAG加熱器出口以后的天然氣管道,為管段2和管段1。管段2內直徑為81 mm,外直徑為89 mm,局部阻力系數取0.1,長度為20 m。管段1內直徑為207 mm,外直徑為219 mm,局部阻力系數取0.1,長度為15 m。
4.2 計算結果與分析
對管道的數學模型進行編程求解,得到各節點的密度、溫度、絕對壓力,見表1。
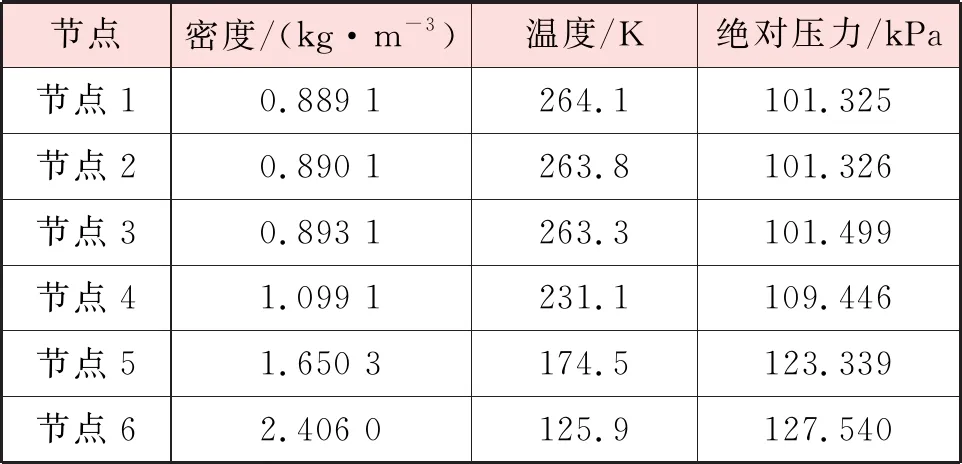
表1 管道的數學模型計算結果
從表1可知,LNG儲罐處安全閥背壓(安全閥出口絕對壓力)為127.540 kPa,安全閥出口溫度為125.9 K。當管段2、4、5長度縮短一半時,其他參數不變,經計算,此時LNG儲罐處安全閥背壓減小至117.14 kPa,安全閥出口溫度降低至125.7 K。當管段6起點質量流量從120 kg/h減小至60 kg/h時,其他參數不變,經計算,此時LNG儲罐處安全閥背壓減小至109.49 kPa,安全閥出口溫度降低至125.5 K。因此,安全閥的背壓不是一個確定的值。
5 結論
在LNG氣化站放散系統設計時,設計人員應當考慮安全閥的背壓與放散量、天然氣組成、安全閥前天然氣的壓力和溫度、環境溫度、放散管道各管段的長度和管徑等許多因素有關,通過對天然氣放散管道進行計算,來合理地確定安全閥選型及放散管道的管徑。

