水處理絮凝動力學研究進展

樊 琦

(江西省水投勘測設計有限公司，江西 南昌 330029)

絮凝是水處理中最常見和最重要的水處理工藝，絮凝效果的好壞會對后續水處理工藝的負荷和最終出水水質產生直接影響[1-2]。水處理通過絮凝使水中的膠體顆粒脫穩和脫穩后的膠體聚集成大的聚集體，并且達到一定的強度，進而通過沉淀去除[3-4]。

為了更加深入地認識絮凝時膠體顆粒發生絮凝的具體過程，以便更好地控制絮凝發生的條件，充分發揮絮凝的作用，需進行動力學方面的研究。本文闡述了水處理絮凝動力學機理和模型理論的研究進展、缺陷以及未來的研究方法。

1 水處理絮凝動力學機理

水處理絮凝動力學主要著重于絮凝過程中顆粒粒徑、濃度等隨時間的減少過程，研究絮凝動力學就是要研究絮凝過程中顆粒狀態的變化，了解數目多而體積小的顆粒如何逐步演變為數目少而體積大的顆粒，進而通過建立數學模型定量描述該變化過程[5-6]。

水處理中絮凝過程需要利用水流流動過程中的能量消耗，促使水中膠體顆粒相互接觸并發生碰撞，逐步形成尺寸較大的絮體，最終達到使顆粒物沉降分離的目的[7]。國內外研究學者對水處理絮凝動力學問題進行了較為廣泛的研究，得出了慣性效應是絮凝動力學致因[8-9]。顆粒之間相互碰撞的機理有3種[10-13]：由于液體分子熱運動而使膠體顆粒產生布朗運動(Brownian motion，Br)引導的異向絮凝、水力和機械攪拌等外力產生流體剪切作用(Shear，Sh)引導的同向絮凝以及顆粒間沉降速度差異(Differential sedimentation,Ds)引導的差速沉降絮凝。絮凝過程中由于水流的強烈紊動，顆粒間的差速沉降作用表現得很微弱，尤其是在絮凝的開始階段，細小顆粒的沉速很小，不同顆粒間的沉速差異也很小，因此，由沉速差異而產生的接觸碰撞，在絮凝過程中一般可以忽略不計。

2 水處理絮凝動力學模型

國外學者在20世紀早期就已經開展了對絮凝動力學的研究，為了合理定量地描述絮凝動力學，提出了很多理論及絮凝動力學模型。

2.1 Smoluchowski模型

最早描述絮凝顆粒碰撞作用規律的絮凝動力學模型是1917年的Smoluchowski公式[14-15]：

(1)

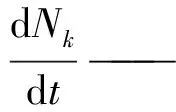
同時給出了布朗運動(異向絮凝)和層流剪切(同向絮凝)的顆粒碰撞頻率函數：

(2)

(3)

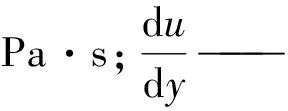
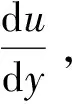
Smoluchowski假設水流所處狀態為層流，碰撞只發生在兩顆粒之間且均為有效碰撞；絮體一旦形成，則不會再破碎；所有微粒(包括絮體)粒徑均是單分散的且均為實心球體[16-18]。這些假設均與后續的研究結果不相符，Sutherland[19]發現絮凝是簇團(若干微小顆粒聚集形成)之間發生碰撞形成的；膠體顆粒之間受靜電荷斥力和范德華力影響，使部分顆粒碰撞后無法聚集，形成無效碰撞[20]。絮凝是一個絮體“生長—破碎—再生長”的過程[21-24]。另外，李振亮等[25]發現絮體顆粒粒徑并不是均一分布的，且實際中的絮體顆粒并不是實心球體。Wang W等[26]在研究3種鋁系絮凝劑去除腐殖酸的效率過程中，發現絮體內部存在一系列的孔隙且較大尺度的絮體同時存在多種孔道結構。

這幾個假設使問題變得更簡單了，但是與實際情況產生了較大偏離，所以Smoluchowski的絮凝動力學模型僅局限于層流條件下的絮凝過程，不能直接用于分析實際發生的許多絮凝現象。

2.2 改進的Smoluchowski模型

Camp和Stein[27]對Smoluchowski方程進行了修正，定義了均方速度梯度G，并用紊流的能量耗散ε與流體的運動黏滯系數ν的比值的平方根來表示紊流狀態下的速度梯度，得出了紊流情況下的絮凝動力學理論公式。

(4)

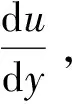
(5)

(6)

式中G——速度梯度，s-1；vi、vj——顆粒i、j的沉降速率，cm/s。

絮凝由以上三者單獨或者協同作用，所以絮凝過程中的綜合碰撞頻率為：

β(i,j)=β(i,j)Br+β(i,j)Sh+β(i,j)Ds

(7)

Camp和Stein通過紊流絮凝速度梯度G理論，修正了Smoluchowski方程僅限于層流條件的問題，建立起了紊流條件下的絮凝動力學模型，彌補了紊流絮凝動力學理論的空白，能夠很好地解釋實際應用中的許多絮凝現象，至今仍是許多水處理中絮凝設計和運行的重要參數[28-30]。

該理論在得出綜合碰撞頻率函數時，只是對3種碰撞頻率做簡單的加和，忽略了3種作用之間的相互關聯性[31-32]。研究表明，為使絮凝順利進行，前期速度梯度值一般較高，后期速度梯度應逐漸減小[33-34]。而Camp和Stein公式采用整體平均G值作為控制絮凝過程的指標，并沒有反映這個規律。

Du G L等[35]將分形理論引入絮凝動力學的研究，提出了分形模型下的碰撞頻率函數：

(8)

(9)

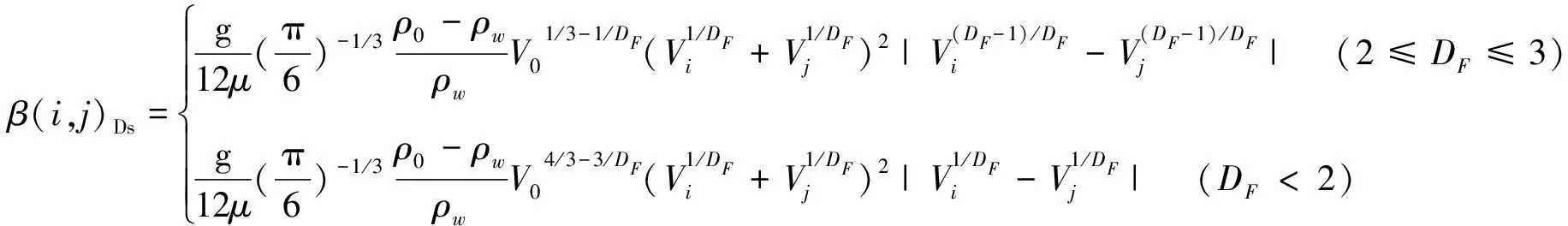
(10)

式中Vi、Vj——i級和j級顆粒的體積，cm3；V0——顆粒的初始體積，cm3；ρ0、ρw——初始顆粒和液體的密度，g/cm3；DF——顆粒的分形維數。

研究表明，分形維數是絮體重要的結構參數，能夠反映真實的絮體結構特征[36-37]。當顆粒的強度不變時，如果能耗增加、G值增大，則絮體的分形維數增加；反之則減小。絮凝過程應保證絮體達到一定的分形維數，同時，為了防止絮體破碎，應增加絮體的強度。所以，在絮凝前期，應保證較高的能量輸入、較強的剪切強度，以增加絮體的尺度與分形維數；絮凝后期，應減少能量輸入、降低剪切強度，以保證絮體強度的增加[38-39]。分形維數的引入，優化了Camp和Stein公式無法反映G值變化規律、忽略絮體破碎和重組過程的缺陷，進一步揭示了絮凝動力學的內在過程，推動了絮凝動力學的發展。但是Du G L等假設絮體碰撞前后的分形維數保持不變，與實際的絮凝動力學過程不相符。

2.3 微渦旋理論模型

Kolmogorov[40]提出了紊流的局部各向同性理論，認為紊流是由一系列大小不一的渦旋組成的渦旋運動，只有渦旋的長度尺度與顆粒粒徑相近或相等時，才能最大限度地促進絮體旋轉，增加與其他顆粒發生碰撞的幾率，提高絮凝效果。此時，渦旋的長度尺度被稱為渦旋尺度(微尺度)，在該尺度下渦旋的速度梯度最大，有利于顆粒的碰撞：

(11)

Saffman和Turner[41]在Kolmogorov理論的基礎上提出了紊流碰撞頻率函數：

(12)

該式形象地揭示了紊流條件下的絮凝動力學致因，能較好地描述紊流條件下的水處理絮凝過程，但是利用紊流能量耗散來描述該過程，不能揭示顆粒之間碰撞的微觀本質。

Levich[42]在紊流中取一球形控制體，將顆粒的碰撞次數看作是單位時間內顆粒通過球形控制體表面進入的平均總數，最終得到了各向同性紊流條件下顆粒的碰撞頻率函數，此時λ=d：

(13)

式中d——顆粒直徑，cm；N——顆粒濃度，個/cm3。

微渦旋理論為后來的學者對紊流絮凝動力學的研究奠定了理論基礎，但只提出了尺度與顆粒粒徑相近或相等時的渦旋的絮凝作用，至于比顆粒尺寸大的渦旋對絮凝是否有貢獻也無直接證據，可見該理論尚不完整。

2.4 群體平衡模型

Kumar S和Ramkrishna D等提出了群體平衡模型[43-45]，用來描述在活性污泥絮凝過程中給定尺寸的絮體數量的變化率。其模型如下：

(14)

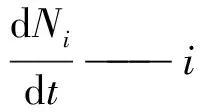
該模型將絮凝看作是絮體聚集和破碎達到平衡的過程，可以計算出絮體尺寸大小的群體分布以及絮體強度隨時間的演變過程[46]。基于該公式研究絮體聚集與破碎的絮凝動力學，取得了許多的成果。Ricardo I等[47]、Lattuada M等[48]利用群體平衡方程來描述紊流剪切流條件下的混凝動力學以及絮體聚集、破碎和重組隨時間的演變關系，發現模型與實驗數據具有很好的一致性。Golzarijalal M等[49]采用群體平衡模型和CFD相結合的方法，對小球藻絮凝過程中的動力學進行了研究，得到了計算微藻絮凝過程中碰撞頻率和破碎率的詳細模型。宋光春等[50]建立了以群體平衡模型為基本框架的水合物聚集動力學模型，對模型聚集核和破碎核的計算方法進行了選取和改進，研究結果為管道流動安全保障提供了技術支持。可見群體平衡模型的提出，為研究絮凝動力學提供了一種重要的方法，但是該模型只停留在顆粒濃度變化的層面，而沒有深入揭示絮凝動力學的內在致因。各絮凝動力學模型的適用條件和優缺點對比見表1。

表1 絮凝動力學模型的適用條件和優缺點對比

除了上述絮凝動力學模型，還有許多的學者也做過相關絮凝動力學的研究。Xiang L等[51]對CPAM的聚合動力學進行了研究，發現其符合一級動力學模型。李國棟等[52]研究了絮凝過程中絮凝劑投加量對絮體結構和絮凝動力學的影響，發現絮體結構會發生重組和排列，絮體密實度會隨著分形維數的增加而增加。丁進鋒等[53]對PAC絮凝小球藻的動力學進行研究，通過數據擬合發現PAC對小球藻的絮凝過程符合二級動力學模型。這些學者均對絮凝動力學過程進行了探索和研究，對促進絮凝動力學的發展具有重大的意義，但是都未能提出系統的絮凝動力學模型描述絮凝過程，在今后的研究中需要引起特別關注。

3 結語

水處理絮凝動力學旨在研究絮凝時絮體顆粒的狀態變化過程，國內外研究學者提出了許多模型描述絮凝動力學。Smoluchowski首先提出了膠體顆粒的絮凝動力學方程，由于做出的假設使理論與實際絮凝過程產生了較大偏離，僅局限于層流條件下的絮凝過程；后來的研究學者根據速度梯度G、碰撞頻率函數β以及分型理論對Smoluchowski模型進行了改進，考慮了顆粒的分形特征，解決了該理論忽略絮體破碎與重組的問題；紊流局部各向同性理論的提出，為后來的學者對紊流絮凝動力學的研究奠定了理論基礎，但由于未能說明比顆粒尺寸大的渦旋對絮凝是否有貢獻，其完整性受到質疑；群體平衡模型雖只停留在顆粒濃度變化的層面，不能反映絮凝動力學的內在致因，但其為絮凝動力學的研究提供了一種重要的方法，對解釋常見的絮凝現象具有重大意義。

近年來出現的絮凝動力學模型逐漸地將絮體的形態結構(數量、大小、分形維數等)以及渦旋形態大小等因素考慮在內，為進一步研究絮凝動力學的內在過程指明了方向。今后的研究需綜合考慮這些因素，同時結合實際情況作出假設，才能得出能全面真實反映絮凝過程的動力學模型。