基于序列二次規(guī)劃法的導(dǎo)彈鴨舵/尾舵復(fù)合控制技術(shù)研究

黃魯豫，徐勝利，張明環(huán)

(1. 西北工業(yè)大學(xué)航天學(xué)院，陜西 西安 710072；2. 上海機電工程研究所，上海 201109)

0 引 言

未來的空中威脅具有高速、高隱身、寬空域以及高機動特征，這些特征對下一代攔截彈的設(shè)計提出了嚴(yán)峻的挑戰(zhàn)，需要其適應(yīng)大范圍的空域及速域的變化。與現(xiàn)役導(dǎo)彈相比，下一代導(dǎo)彈的作戰(zhàn)高度需求更高，甚至要求其在20～30 km執(zhí)行任務(wù)。在此環(huán)境下，由于空氣非常稀薄，導(dǎo)彈氣動舵控效率很低，舵容易處于飽和狀態(tài)。如繼續(xù)采用傳統(tǒng)的控制方式，導(dǎo)彈在20 km以上高度飛行時已基本不具備過載能力，無法滿足快速響應(yīng)、大機動能力的任務(wù)需求[1-3]。

目前，國內(nèi)外針對該問題的解決方案集中于采用氣動力/直接力的復(fù)合控制方式，以期提升導(dǎo)彈的響應(yīng)速度和機動能力[4-7]。與單純依靠氣動力控制相比，采用復(fù)合控制方式的導(dǎo)彈過載響應(yīng)上升時間下降了一個數(shù)量級，而且可用過載的大小不受導(dǎo)彈飛行高度的影響，因此能夠在很大程度上提高導(dǎo)彈控制系統(tǒng)的性能。

雖然氣動力/直接力的復(fù)合控制方式是提升導(dǎo)彈控制能力的一種有效手段，但其代價是要在導(dǎo)彈上增加額外的能源，不僅增加全彈重量，還會擠壓有效載荷的空間。針對該問題，本文提出了一種新的解決思路，通過增加一組鴨舵來增加導(dǎo)彈在高空時的可用過載，并設(shè)計了一種鴨舵/尾舵復(fù)合控制方法以保證導(dǎo)彈在全飛行空域和速域都具備快速響應(yīng)和大機動過載的能力。

1 導(dǎo)彈建模

1.1 六自由度模型

本文假定的導(dǎo)彈氣動外形如圖1所示。導(dǎo)彈采用軸對稱外形，安裝有4片鴨舵和4片尾舵。俯仰通道和偏航通道采用鴨舵、尾舵聯(lián)合控制，滾轉(zhuǎn)通道由尾舵控制。

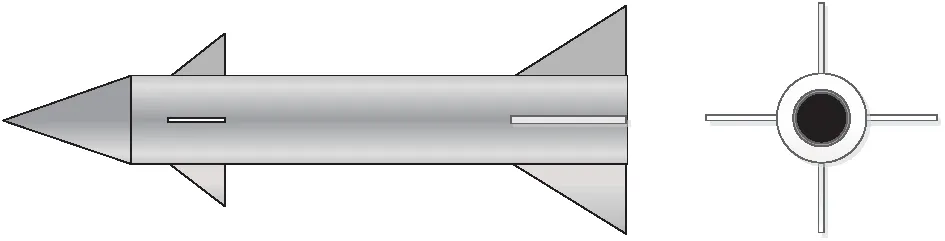
圖1 導(dǎo)彈氣動外形Fig.1 The aerodynamic shape of missile

為簡化彈體動力學(xué)模型，把導(dǎo)彈視為剛體，暫時忽略地球自轉(zhuǎn)的影響。導(dǎo)彈的六自由度模型如式(1)～(4)所示。

(1)

(2)

(3)

(4)

式中：ωx,ωy,ωz為三個姿態(tài)角速度；Mx,My,Mz為3個方向的力矩；Jx,Jy,Jz為3個轉(zhuǎn)動慣量；x,y,z為發(fā)射系下導(dǎo)彈的位置坐標(biāo)點；v為導(dǎo)彈飛行速度；θ,φ為彈道傾角和彈道偏角；?,ψ,γ為俯仰角、偏航角和滾轉(zhuǎn)角；α,β為攻角和側(cè)滑角。

1.2 線性化數(shù)學(xué)模型

對軸對稱導(dǎo)彈數(shù)學(xué)模型進(jìn)行小擾動線性化，簡化條件為：

1) 采用系數(shù)凍結(jié)法，即彈道上某一時刻t的導(dǎo)彈飛行速度v、高度H、推力P、質(zhì)量m、轉(zhuǎn)動慣量J均不變。

2) 攻角α、側(cè)滑角β均為小量，即sinα≈α、cosα≈1、sinβ≈β、cosβ≈1。

3) 控制系統(tǒng)保證實現(xiàn)滾轉(zhuǎn)角穩(wěn)定，并有足夠的快速性。

由此，導(dǎo)彈動力學(xué)模型可線性化為

(5)

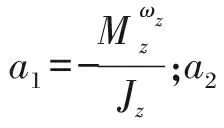
忽略運動學(xué)耦合項-ωxβ，可得導(dǎo)彈縱向通道小擾動線性化模型為

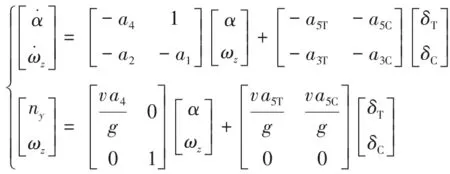
(6)

式中：ny為導(dǎo)彈法向過載；g為重力加速度。

同理，可得導(dǎo)彈橫側(cè)向小擾動線性化模型為

(7)

(8)

式中：nz為導(dǎo)彈側(cè)向過載。

2 鴨舵/尾舵復(fù)合控制算法

以縱向通道為例，導(dǎo)彈鴨舵/尾舵復(fù)合控制系統(tǒng)結(jié)構(gòu)如圖2所示。

注： nyc為法向過載指令；Kny、Kα、Kω為三回路的控制增益系數(shù)；δzc為z通道舵偏控制指令；為積分環(huán)節(jié)；ωz(s)、δz(s)、ny(s)、α(s)分別為ωz(t)、δz(t)、ny(t)、α(t)經(jīng)拉斯變換后得到的頻域信號。圖2 鴨舵/尾舵復(fù)合控制系統(tǒng)結(jié)構(gòu)Fig.2 The canard/tail rudder compound control system structure

俯仰通道舵指令分配方式為

(9)

式中：Kz1,Kz2分別為鴨舵和尾舵的分配系數(shù)。

通過規(guī)劃鴨舵/尾舵的分配系數(shù)(Kz1,Kz2)，可以使作用于導(dǎo)彈的阻力最小化，從而保證導(dǎo)彈的高空過載能力。本文在過載三回路控制系統(tǒng)的基礎(chǔ)上，采用序列二次規(guī)劃法對鴨舵/尾舵分配系數(shù)進(jìn)行以下優(yōu)化設(shè)計，使得

(10)

式中：Cd為阻力系數(shù)。

(11)

3 序列二次規(guī)劃算法原理

一般非線性約束的數(shù)學(xué)規(guī)劃問題是[8-9]：

minf(X)

(12)

式中：X∈Rn是決策變量；f(X)是目標(biāo)函數(shù)；gu(X)和hv(X)分別是不等式約束函數(shù)和等式約束函數(shù)。

利用泰勒展開把非線性約束問題式(12)的目標(biāo)函數(shù)在迭代點Xk簡化成二次函數(shù)，把約束函數(shù)簡化成線性函數(shù)后得到的就是如式(13)所示的二次規(guī)劃問題。

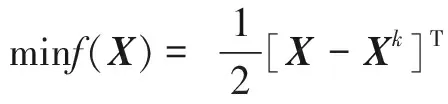
(13)

此問題是原約束最優(yōu)化問題的近似問題，但其解不一定是原問題的可行點。為此，令S=X-Xk，將上述二次規(guī)劃問題變成關(guān)于變量S的問題，即為

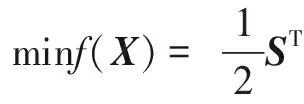
(14)

令H=2f(Xk)

C=f(Xk)

Aeq=[h1(Xk),h2(Xk),…,hm(Xk)]T

A=[g1(Xk),g2(Xk),…,gp(Xk)]T

Beq=[h1(Xk),h2(Xk),…,hm(Xk)]T

B=[g1(Xk),g2(Xk),…,gp(Xk)]T

(15)

將式(14)變成二次規(guī)劃問題的一般形式，即為

(16)

求解此二次規(guī)劃問題，將其最優(yōu)解S*作為原問題的下一個搜索方向Sk，并在該方向上進(jìn)行原約束問題目標(biāo)函數(shù)的約束一維搜索，即可得到原約束問題的一個近似解Xk+1。反復(fù)迭代該過程，直至求得最優(yōu)解。

4 仿真驗證

為驗證本文控制算法的有效性，構(gòu)建以下仿真場景。

1) 目標(biāo)從350 km外進(jìn)入戰(zhàn)區(qū)，側(cè)向偏差z=100 m，飛行速度為1 800 m/s，飛行高度為30 km，在距離導(dǎo)彈70 km 時以3g過載做側(cè)向機動進(jìn)行規(guī)避，機動時間5 s。

2) 導(dǎo)彈以70°俯仰角從地面發(fā)射，爬升至近30 km高度后對目標(biāo)進(jìn)行跟蹤攔截。

3) 仿真環(huán)境為Matlab/Simulink，仿真步長為0.001 s。

仿真結(jié)果如圖3～11所示。

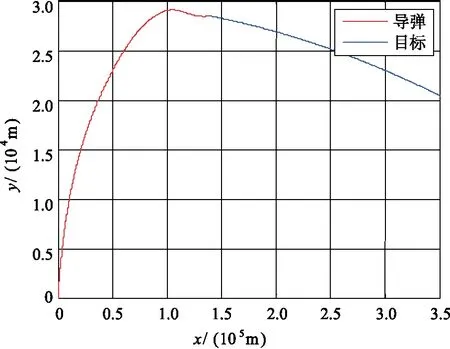
圖3 縱向平面飛行彈道Fig.3 The trajectory in longitudinal plane

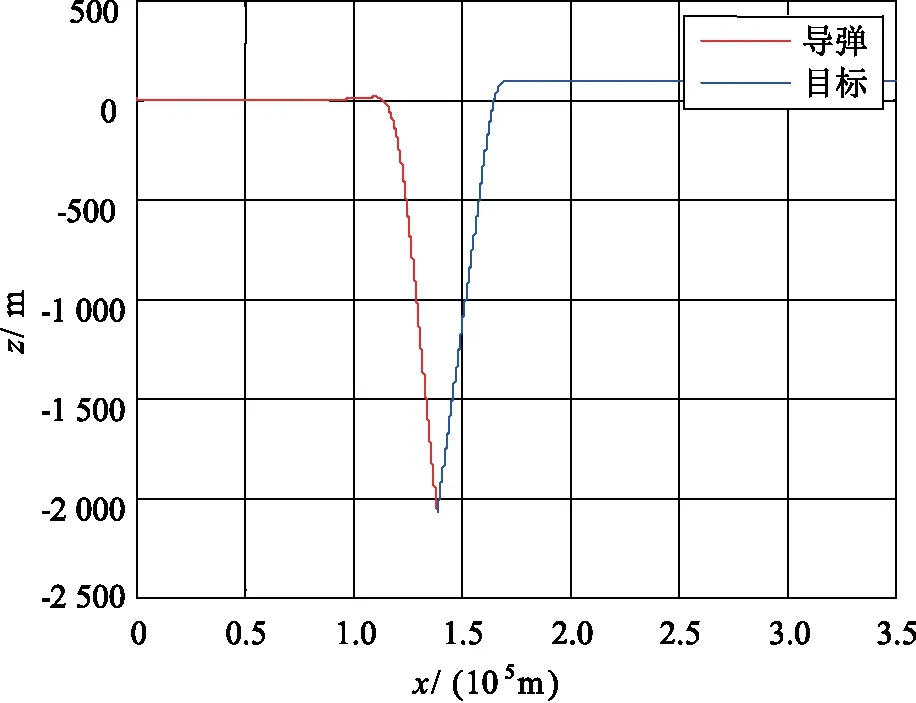
圖4 橫側(cè)向平面飛行彈道Fig.4 The trajectory in horizontal plane

從圖3和圖4可以看出，在30 km的高空，導(dǎo)彈擊中了目標(biāo)，脫靶量小于3 m。

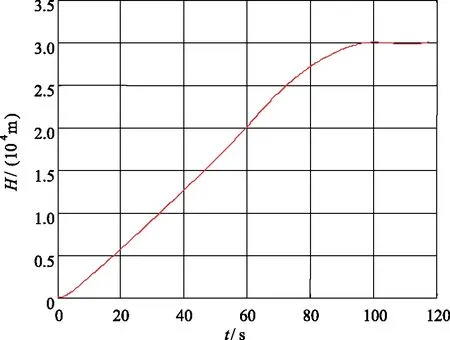
圖5 導(dǎo)彈高度曲線Fig.5 The height curve of missile

從圖5可以看出，導(dǎo)彈爬升至30 km后，姿態(tài)和軌跡能夠迅速穩(wěn)定收斂，證明了本文控制算法具有良好的動態(tài)特性和穩(wěn)態(tài)特性。

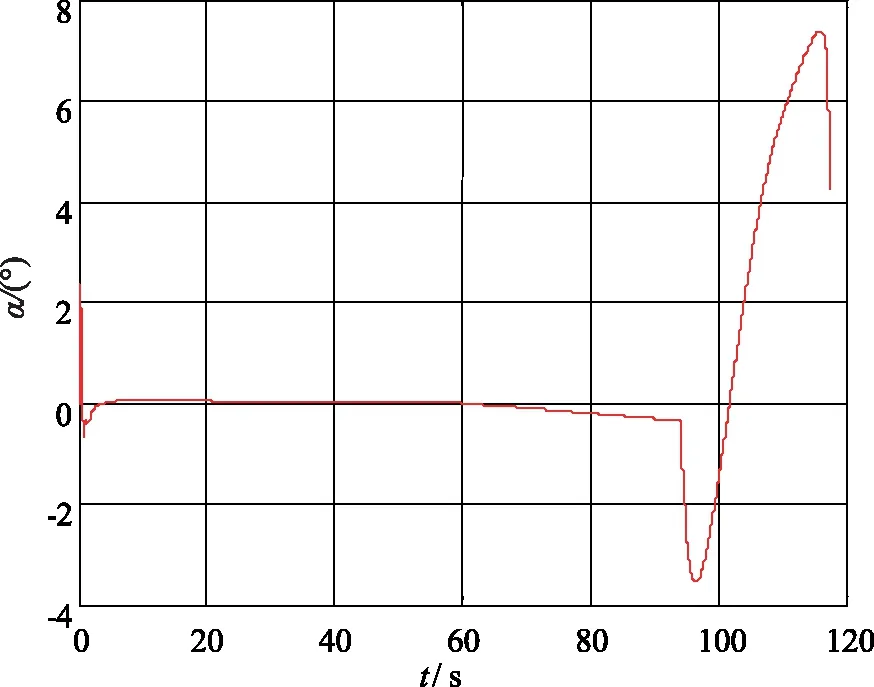
圖6 導(dǎo)彈攻角曲線Fig.6 The attack angle curve of missile

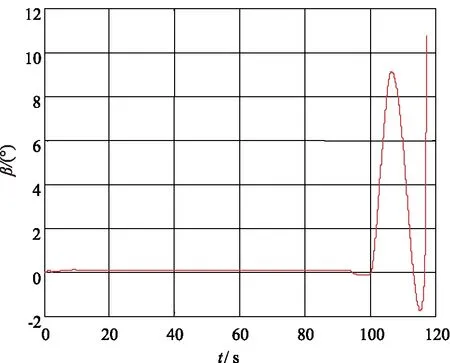
圖7 導(dǎo)彈側(cè)滑角曲線Fig.7 The sideslip angle curve of missile

從圖6和圖7可以看出，導(dǎo)彈在做機動時，攻角和側(cè)滑角始終處于較小的狀態(tài)。

圖8 導(dǎo)彈法向過載曲線Fig.8 The normal overload curve of missile

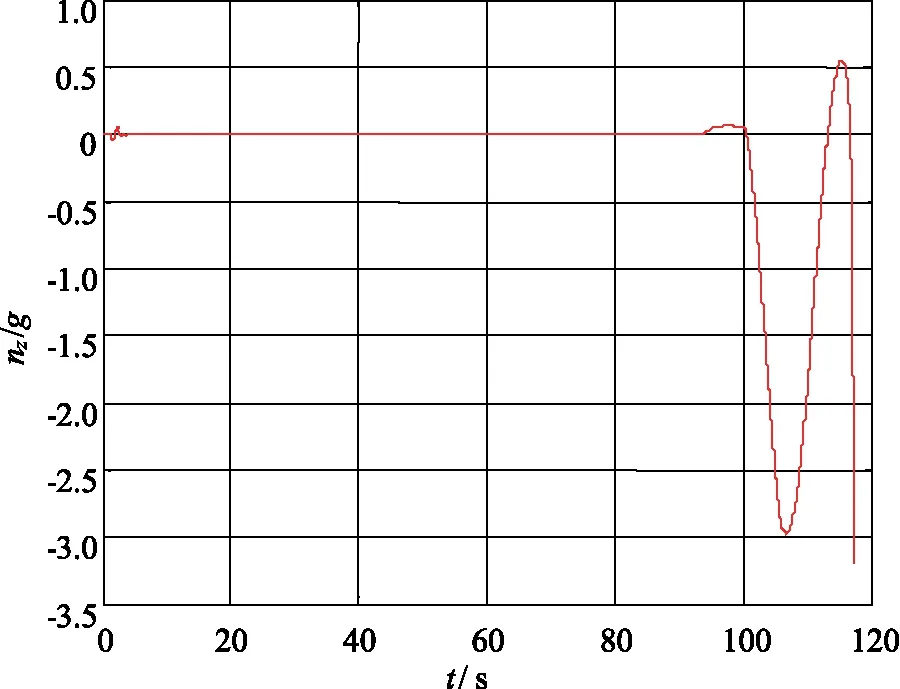
圖9 導(dǎo)彈側(cè)向過載曲線Fig.9 The lateral overload curve of missile

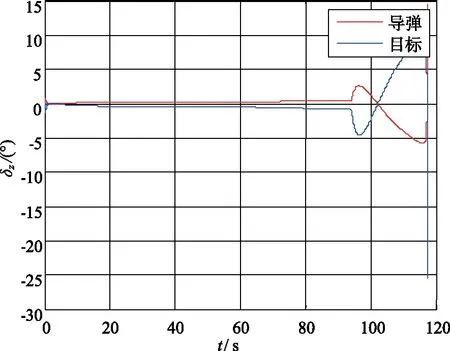
圖10 導(dǎo)彈俯仰通道舵偏角曲線Fig.10 The pitching channel rudder deflection angle curve of missile

從圖8和圖9可以看出，在30 km的高空，導(dǎo)彈仍然具備3g以上的過載機動能力，證明了本文基于序列二次規(guī)劃法設(shè)計的鴨舵/尾舵復(fù)合控制策略能夠保證導(dǎo)彈的高空機動能力。

圖11 導(dǎo)彈偏航通道舵偏角曲線Fig.11 The yaw channel rudder deflection angle curve of missile

從圖10和圖11可以看出，在30 km的高空，導(dǎo)彈在做3g的機動時，舵偏角小于15°，相對飛行器通常采用的25°限幅值仍有一定空間，表明導(dǎo)彈具備潛在的更大的機動能力，也進(jìn)一步證明了本文算法的有效性。

5 結(jié)束語

本文設(shè)計了導(dǎo)彈鴨舵 / 尾舵復(fù)合控制系統(tǒng)，并采用序列二次規(guī)劃法對鴨舵 / 尾舵的舵指令分配策略進(jìn)

行了優(yōu)化設(shè)計。通過仿真驗證，證明了本文所設(shè)計的控制系統(tǒng)不但具有良好的動態(tài)特性和穩(wěn)態(tài)特性，還能夠保證導(dǎo)彈在高空仍具備高機動能力。本文的研究為未來導(dǎo)彈的設(shè)計提供了一種新的思路，具有較高的應(yīng)用價值和工程意義。