液壓機械復合傳動系統模式切換過程同步控制

曹付義,李豪迪,席志強,徐立友,3

(1.河南科技大學車輛與交通工程學院,471003,河南洛陽; 2.河南科技大學機械裝備先進制造河南省協同創新中心,471003,河南洛陽; 3.河南科技大學拖拉機動力系統國家重點實驗室,471039,河南洛陽)

synchronous control

與單一模式的液壓機械復合傳動系統相比,雙模式液壓機械復合傳動(DHMT)系統在一定程度上兼顧了分速匯矩模式在低速段具有高效率和分矩匯速模式在高速段具有低液壓功率分流比的優點,適合于具有多工況傳動特點的大功率特種車輛使用,是未來液壓機械復合傳動系統研究的一個新方向[1]。

DHMT系統通過采用不同模式銜接切換的方式來擴大系統的調速范圍,這樣需要考慮分流模式切換機構以及匯流模式切換機構對系統分流機構和匯流機構的平順切換問題。切換過程中不同類型的分、匯流機構轉速銜接不匹配以及分、匯流模式切換機構轉速過渡時間長,造成液壓調速系統轉速發生突變,出現系統動力中斷、沖擊度較大等問題,對系統模式切換品質產生影響[2]。

國內外學者針對單一模式下的液壓機械復合傳動系統的設計方法[3-6]、傳動特性[7-10]、換段品質影響因素[11-14]以及改善換段品質方法[15-18]等方面進行了大量研究。與單一模式液壓機械復合傳動系統相比,針對DHMT系統的研究較少。杜玖玉等為了解決一段式液壓機械無級傳動裝置不能滿足重型車輛傳遞大功率的問題,設計了一種新型雙模式復合分流式液壓機械傳動方案,并分析了液壓機械復合傳動的速比、轉矩以及功率等傳動特性[19];于亞鵬提出了一種兩段式液壓機械復合變速器,該變速器兼具分矩匯速和分速匯矩兩種工作模式,通過對其進行傳動特性分析,表明了所設計方案具有優良的調速特性、起步特性和行駛特性[20];Masahiro等設計了液壓機械式變速器,其耦合了分速匯矩與分矩匯速的設計理念,通過設置較低的比例溢流閥閾值,利用液壓系統的耦合性來降低模式切換的沖擊[21];曹付義等針對所設計的多模式液壓機械復合傳動裝置,進行了不同模式下的基礎特性研究,得出其具有傳動平穩和效率高等優點[22],但有關液壓機械復合傳動系統模式切換控制的研究相對較少。

本文針對一種雙模式液壓機械復合傳動系統,對其進行動力學分析,并基于液壓調速系統同步切換條件,將模式切換過程歸納為3個階段,通過對切換流程的理論分析,提出了一種液壓調速系統轉速同步補償控制和切換機構轉矩同步補償控制的模式切換同步控制方法,通過仿真與實驗,揭示了DHMT系統的模式切換規律,驗證了該控制方法的有效性。

1 DHMT系統構型及動力系統建模

1.1 DHMT系統構型及動力學模型

本文研究的DHMT系統結構如圖1所示,該結構包括分流模式切換機構、分流機構、液壓調速系統、匯流機構以及匯流模式切換機構等。

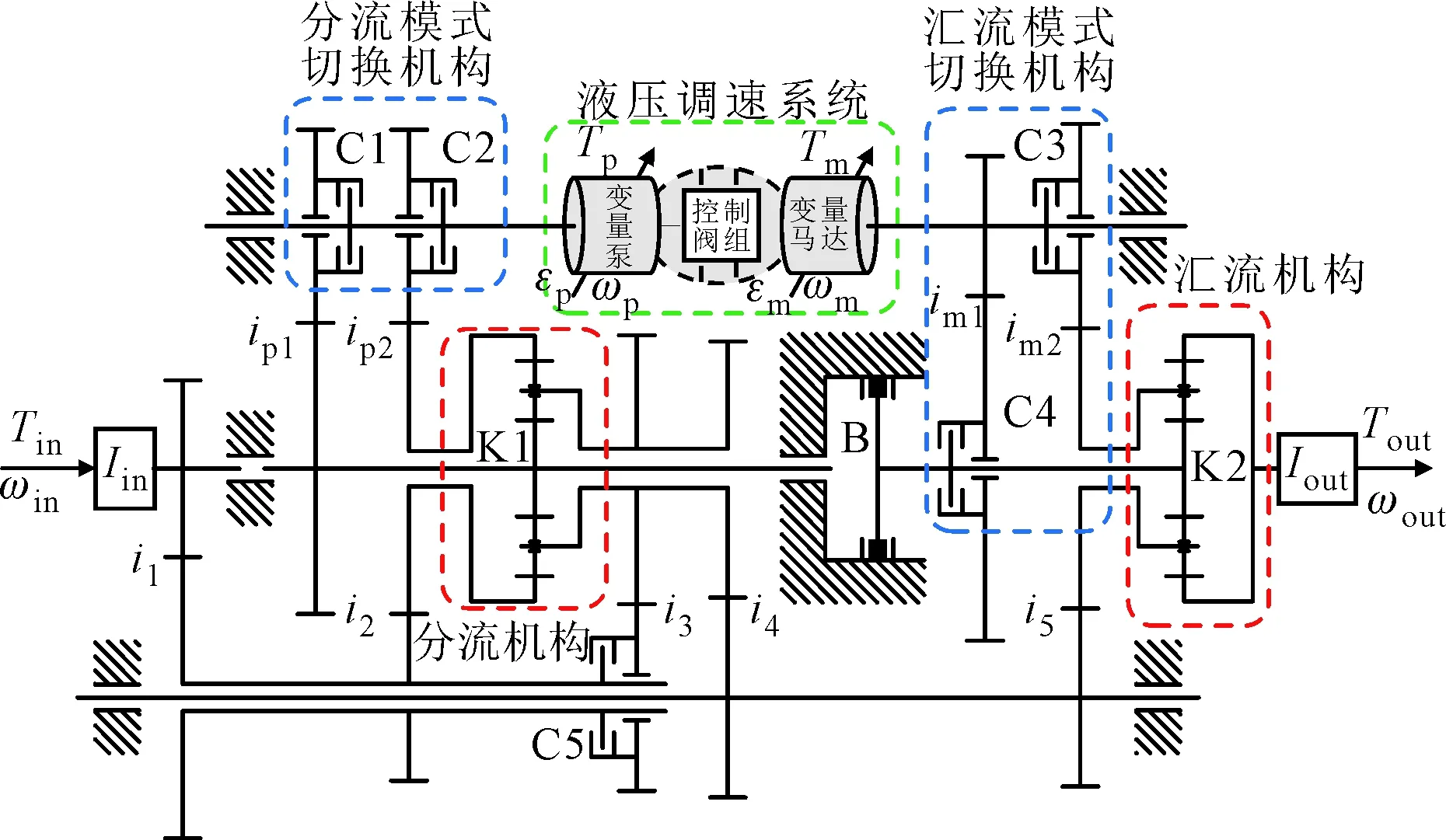
Tin:系統輸入轉矩;ωin:系統輸入角速度;Iin:系統輸入端當量轉動慣量;Tout:系統輸出轉矩;ωout:系統輸出角速度;Iout:系統輸出端當量轉動慣量;K1:分流機構行星排;K2:匯流機構行星排;Tp:變量泵轉矩;ωp:變量泵角速度;εp:變量泵變排量系數;Tm:變量馬達轉矩;ωm:變量馬達角速度;εm:變量馬達變排量系數;C:離合器;B:制動器;i:定軸齒輪傳動比圖1 DHMT系統結構簡圖

DHMT系統通過控制離合器與制動器的不同結合時序,可以實現兩種工作模式,分別為以行星排K1為分速裝置的分速匯矩HM1模式和以行星排K2為匯速裝置的分矩匯速HM2模式,各模式下切換機構的工作狀態見表1。

表1 液壓機械復合傳動系統工作狀態

為了滿足DHMT系統動力性和模式切換過程同步控制的需要,建立分速匯矩HM1模式和分矩匯速HM2模式動力學模型。為研究簡便,建模時僅考慮系統構件和負載的轉動慣量,忽略彈性環節和阻尼的影響,各相關構件以集中質量的形式存在。建立各構件的動力學模型并消去行星排內力及構件間相互作用力,分速匯矩HM1模式動力學模型為

(1)

分矩匯速HM2模式動力學模型為

(2)

式中:Tout為系統輸出轉矩;ωout為系統輸出角速度;Iout為系統輸出端當量轉動慣量;k1、k2分別為行星排K1、K2的特征常數;Tin為系統輸入轉矩;ωin為系統輸入角速度;Iin為系統輸入端當量轉動慣量;Dm為變量馬達最大排量;εm為變量馬達變排量系數;Dp為變量泵最大排量;εp為變量泵變排量系數;ηm為系統機械路傳遞效率;ηh為液壓調速系統傳遞效率;ωp為變量泵角速度;Ip為變量泵當量轉動慣量;ωm為變量馬達角速度;Im為變量馬達當量轉動慣量;i代表定軸齒輪傳動比。

1.2 液壓調速系統數學模型

在建立變量泵變量馬達調速回路數學模型時,假設連接管道為兩根完全相同的短硬管;液壓泵和馬達的泄漏為層流[23];每個腔室內的壓力是均勻相等的,不考慮流量脈動對系統動態特性的影響,液體密度為常數;輸入信號不發生飽和現象;不考慮補油系統,對變量泵、變量馬達構成的液壓調速系統建立高壓油路流量方程和轉矩平衡方程

(3)

ζ(ph-pl)Dmεm

(4)

式中:Ctm為液壓調速系統總泄漏系數;λ為油液動力黏度;ph為變量泵高壓油口壓力;pl為變量泵低壓油口壓力;V為液壓調速系統的管路總容積;bm為變量馬達黏性阻尼系數;βe為綜合體積彈性模量;ζ為變量馬達的機械摩擦損失系數;Tm為變量馬達轉矩。

1.3 模式切換機構模型

模式切換機構的結合過程中會經歷分離、滑摩和完全結合狀態。分離狀態下,離合器傳遞扭矩和轉速為零;完全結合狀態下,離合器可傳遞全部功率;滑摩狀態下,離合器的傳遞轉矩與離合器主動盤和從動盤的角速度差相關,離合器結合或分離的理論轉矩為

(5)

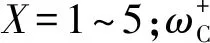
1.4 液壓調速系統同步切換點

以HM1向HM2模式切換為例,分速匯矩HM1模式的輸出角速度為

(6)

式中:ωout_HM1為HM1模式下DHMT系統輸出角速度;ωC2為行星排K2的行星架角速度;ωr2為行星排K2的齒圈角速度;ηV為液壓調速系統的容積效率。

為了盡可能減小切換過程中的沖擊,將采用無動力切換,即切換過程中切斷DHMT系統與動力源的動力連接,故此時行星排K1的行星架的轉速直接受輸出角速度制約,因此行星排K1的行星架的角速度為

(7)

行星排K1的齒圈的角速度為

ωr1=ωin/(i1i2)

(8)

故行星排K1的太陽輪的角速度為

(9)

由式(9)可得變量泵角速度為

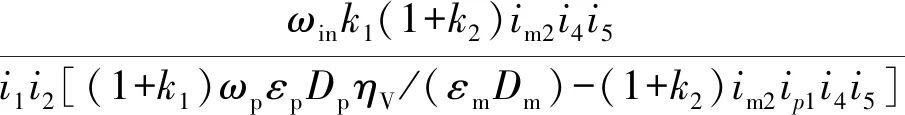
(10)

由式(10)可以得出,當HM1向HM2模式切換時,離合器C2結合,此時主、從動盤角速度差為

(11)

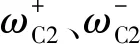
根據式(11)可以看出,為了使模式切換過程中離合器C2進行無速差地結合,可以得到分速匯矩HM1模式向分矩匯速HM2模式切換過程中行星排K1分流機構輸入端的同步切換條件為

(12)

由式(12)可解得,分速匯矩HM1模式向分矩匯速HM2模式切換過程中液壓調速系統變量泵和變量馬達的變排量系數的關系為

(13)

根據式(13)可以看出,模式切換過程中變量泵變排量系數εp是隨變量泵角速度ωp以及變量馬達變排量系數εm變化而變化的非線性關系,故對于DHMT系統的模式切換過程中的排量調節相互獨立且具有滯后性,可將模式切換過程進行階段劃分,從而可簡化切換過程。

2 DHMT系統模式切換過程分析

2.1 切換過程評價指標

模式切換品質評價指標通常是指沖擊度J和滑摩功W,為了更加詳細地反映模式切換過程中DHMT系統的動力性,在原有評價指標基礎上提出切換時間Δt和最大輸出轉矩損失系數ξHM兩個評價指標。

(1)切換時間Δt。切換時間是指從一個模式的穩定狀態轉換到另一個模式穩定狀態后所需要的時間,它是反映模式切換品質的綜合性指標。切換時間過短可能會導致沖擊度過大。因此,良好切換品質的要求是在平順切換的基礎上盡量減少切換時間。

(2)最大輸出轉矩損失系數ξHM。在DHMT系統模式切換過程中,需要對系統輸出轉矩的損失程度進行評價,最大輸出轉矩損失系數可以用切換過程中傳動系統輸出轉矩最小值與切換開始前傳動系統的穩定輸出轉矩之差與切換開始前傳動系統的穩定輸出轉矩的比值表示,即

ξHM=(T0-Tout)/T0

(14)

式中:T0為模式切換前的穩定輸出轉矩。

2.2 模式切換過程分析

DHMT系統的模式切換過程需要控制切換機構的結合與分離,模式切換品質受到多重因素的影響,以HM1向HM2模式切換為例進行切換過程研究,將其切換過程劃分為3個階段,切換過程如圖2所示。

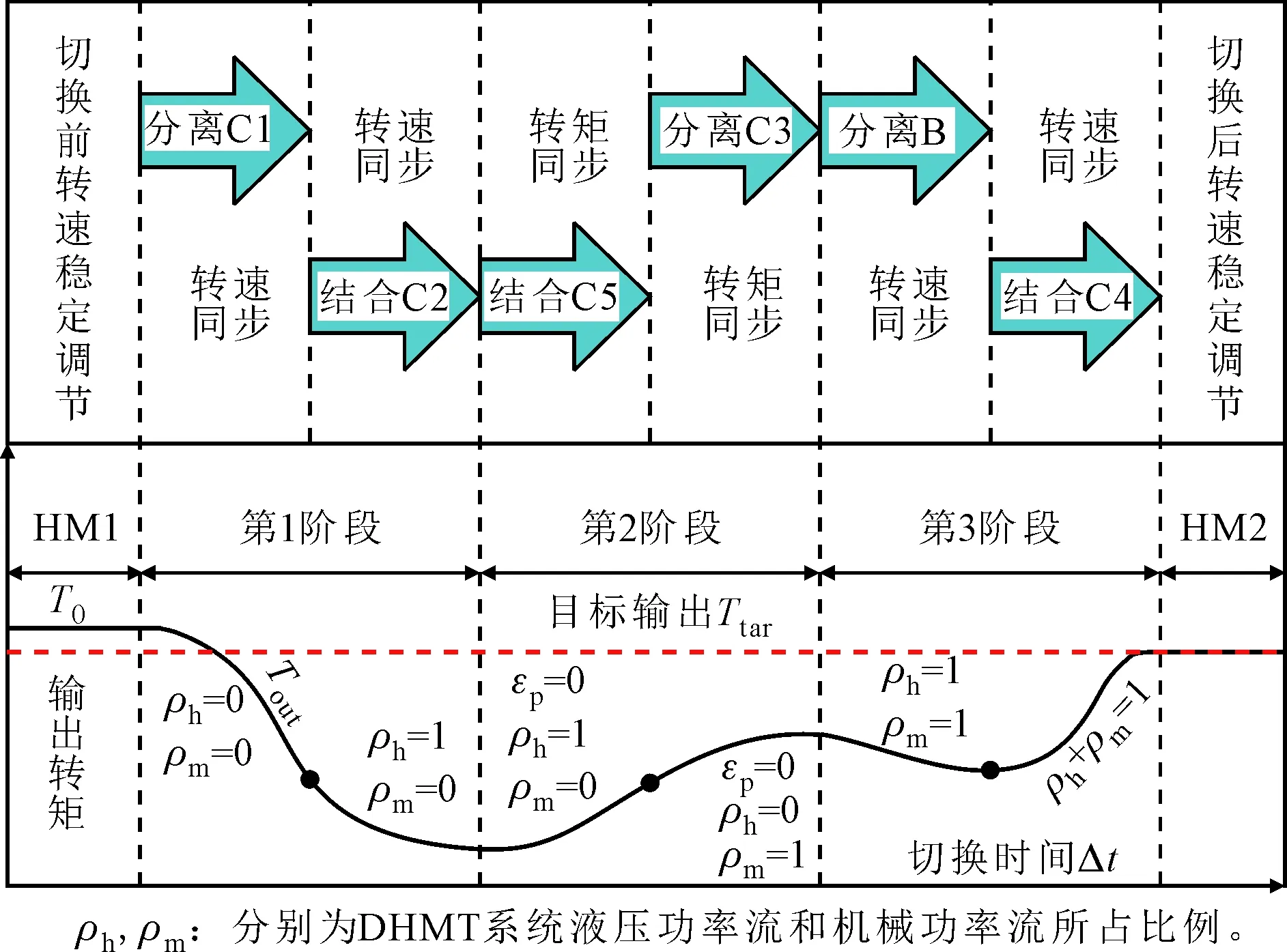
圖2 HM1向HM2模式切換過程示意圖

第1階段(C1分離,C2結合)。為了使離合器C2無沖擊地結合,需要滿足變量泵與離合器C2主動盤角速度相等,此時通過控制系統輸入角速度,即

(15)

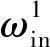
當分流模式切換機構在進行動力切換的過程中,通過控制離合器C1釋放油缸腔壓力,C2離合器的油壓由0逐漸升高,行星排K1的太陽輪由于失去約束而處于游離狀態,機械路功率逐漸降低,此時系統變為純液壓傳動,行星排K2由于機械路轉矩的變化,系統輸出角速度急速降低,此階段系統動力學方程為

(16)

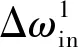
(17)

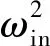
離合器C5在結合過程中,需要保持變量泵的排量為0,系統輸出角速度完全由輸入端決定,待離合器C5完全結合后,逐漸調節變量馬達排量,待輸出角速度穩定后,斷開離合器C3,系統動力學方程為

(18)

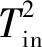
第3階段(B分離,C4結合)。為了防止變量馬達與行星排K2的太陽輪產生干涉,從而造成更大程度上的運動沖擊,首先對制動器B進行解約束,調節變量馬達的變排量系數向最大排量的方向變化,為了減弱因行星排K2轉速耦合產生的擾動,需滿足以下條件

(19)

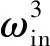
在制動器B斷開和離合器C4結合的重疊時間內,需要保持變量馬達的排量為0,系統輸出轉速由于行星排K2沒有液壓功率的約束而發生短暫的降低,此時輸出轉矩完全受機械功率的影響,較第1階段和第2階段略有提高,此階段系統動力學方程為

(20)

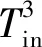
通過以上3個階段的分析,在模式切換過程中系統輸入角速度的總擾動量為

(21)

式中:Δωin為DHMT系統輸入角速度總擾動量。

3 DHMT系統模式切換過程同步控制

模式切換同步控制包括液壓調速系統轉速同步補償控制和切換機構轉矩同步補償控制。HM1向HM2模式切換過程控制方法流程如圖3所示。

液壓調速系統轉速同步補償控制用于抑制系統輸入轉速變化引起的切換機構轉速與液壓元件轉速不匹配問題,為切換機構的平穩結合創造條件;切換機構轉矩同步補償控制通過優化制動裝置結合主、從動盤角速度之差和切換時間,解決模式切換過程中的系統輸出轉矩中斷和沖擊問題。

3.1 液壓調速系統轉速同步補償控制

DHMT系統的輸入角速度擾動量Δωin將會引起離合器結合過程中的轉速波動,以HM1向HM2模式切換為例,離合器C2的結合平順性受到變量泵角速度與系統輸入角速度的影響,即機械系統的擾動影響;離合器C4的結合過程中不僅會受到機械系統角速度擾動的影響,還會受到液壓調速系統輸入擾動的影響。為了使離合器主從動盤的角速度差ΔωC維持在合理范圍之內,以保證離合器平順結合,需通過變量泵或變量馬達的前饋反饋轉速同步補償對DHMT系統輸入角速度擾動進行抑制,前饋反饋轉速同步補償控制方法如圖4所示。

在建立泵馬達調速回路前饋補償數學模型時,采用小信號線性化方法對液壓系統變量馬達斜盤擺角和角速度關系進行線性化處理[24]

(22)

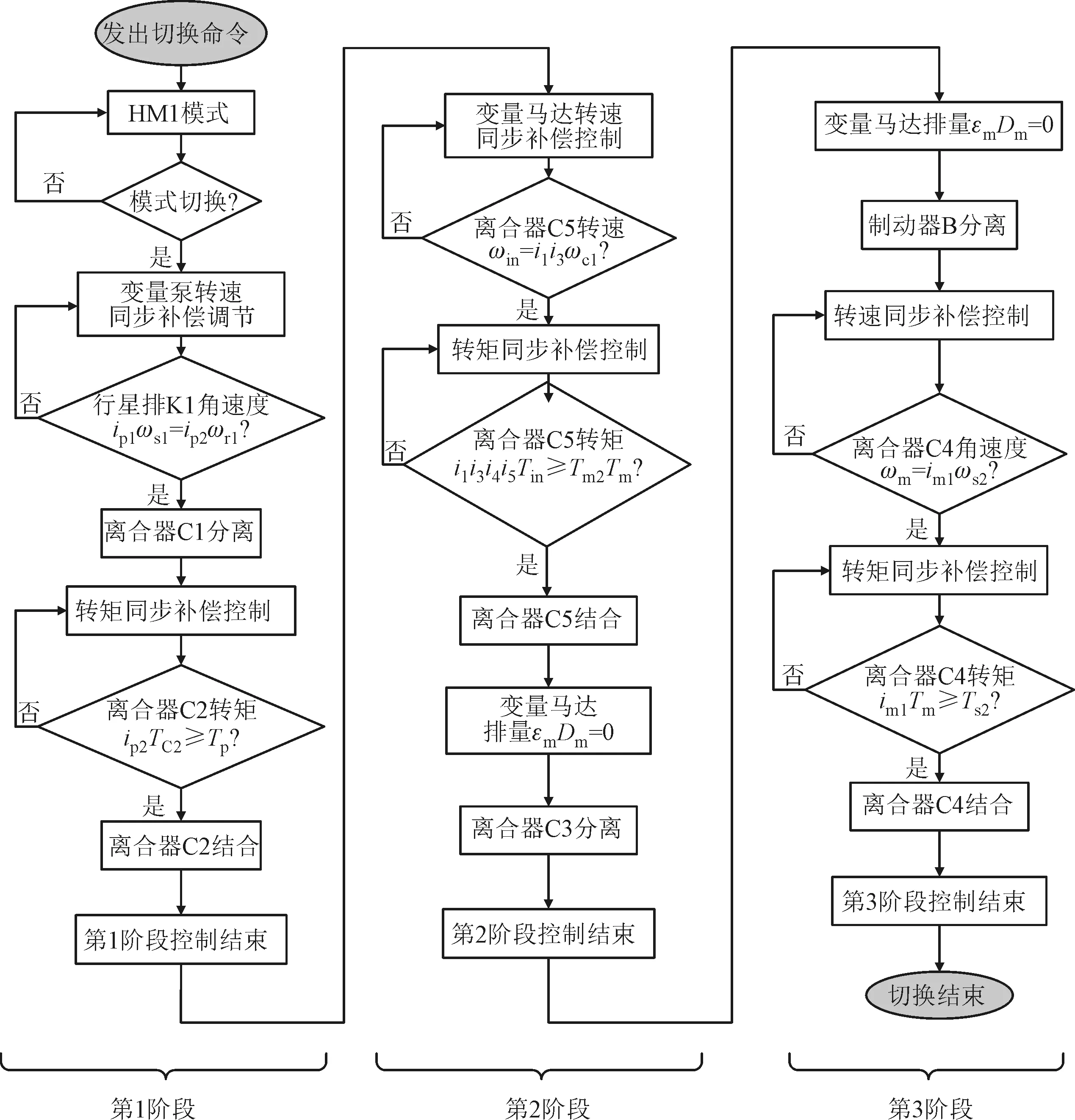
圖3 切換過程控制方法流程

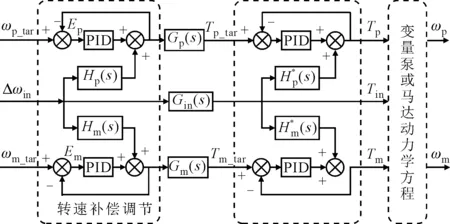
圖4 前饋反饋轉速同步補償控制方法

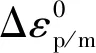
將式(22)代入式(3)(4)中進行拉氏變換,并忽略無窮小量Δεp/mΔωp/m,得到變量泵或變量馬達角速度擾動量Δωp/m與變排量系數變化補償增量方程為

(23)

式中:Gc(s)為變量泵或變量馬達所受角速度干擾與變排量系數補償關系的傳遞函數;Qp/m為變量泵或變量馬達的流量;Δph為液壓調速系統高低壓油路壓力差;Km為排量梯度;s為拉普拉斯算子。

假設變量泵和變量馬達受系統輸入擾動為一階或二階慣性加純延遲環節,即

R(s)=K*/(as+1)e-bs

(24)

式中:R(s)為系統輸入擾動傳遞函數;K*為干擾通道環節比例系數;a為干擾通道慣性環節時間常數;b為干擾通道延遲時間。

根據雙模式液壓機械復合傳動系統前饋反饋轉速補償傳遞函數關系,可以得到液壓調速系統變量泵的轉速/轉矩前饋補償傳遞函數

(25)

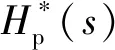
變量馬達的轉速/轉矩前饋補償傳遞函數

(26)

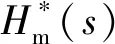
反饋控制過程采用傳統PID調節器,即

Gs(s)=kp+ki/s+kds

(27)

式中:Gs(s)為傳統PID調節器傳遞函數;kp為轉速控制的比例增益;ki為積分環節常數;kd為微分環節常數。

變量泵的轉矩補償傳遞函數為

(28)

變量馬達的轉矩補償傳遞函數為

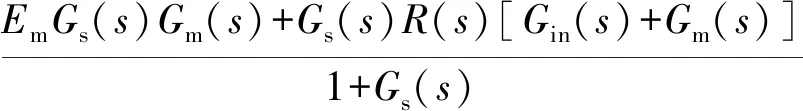
(29)

式中:Ep、Em分別為變量泵、變量馬達目標角速度與實際角速度偏差;Gp(s)為變量泵角速度/轉矩關系傳遞函數;Gm(s)為變量馬達角速度/轉矩關系傳遞函數。

根據所得到的變量泵或變量馬達的轉矩補償傳遞函數,將其代入式(1)(2)可得到對應的轉速同步補償控制量,在此不再詳細贅述。

3.2 切換機構轉矩同步補償控制

在當前模式離合器還未完全分離,目標模式離合器逐漸結合的過程中,系統輸入轉矩與輸出轉矩處于動力耦合階段,由系統輸入角速度擾動引起的輸入轉矩變化,若要離合器結合沖擊控制在合理范圍之內,就必須通過液壓元件的轉矩反饋補償控制對系統波動進行抑制,以達到切換機構平穩結合的作用。DHMT系統輸入轉速轉矩滿足關系

Tin=(τins+1)-1f(ωin,Δωin)

(30)

式中:τin為DHMT系統輸入角速度慣性環節時間常數。

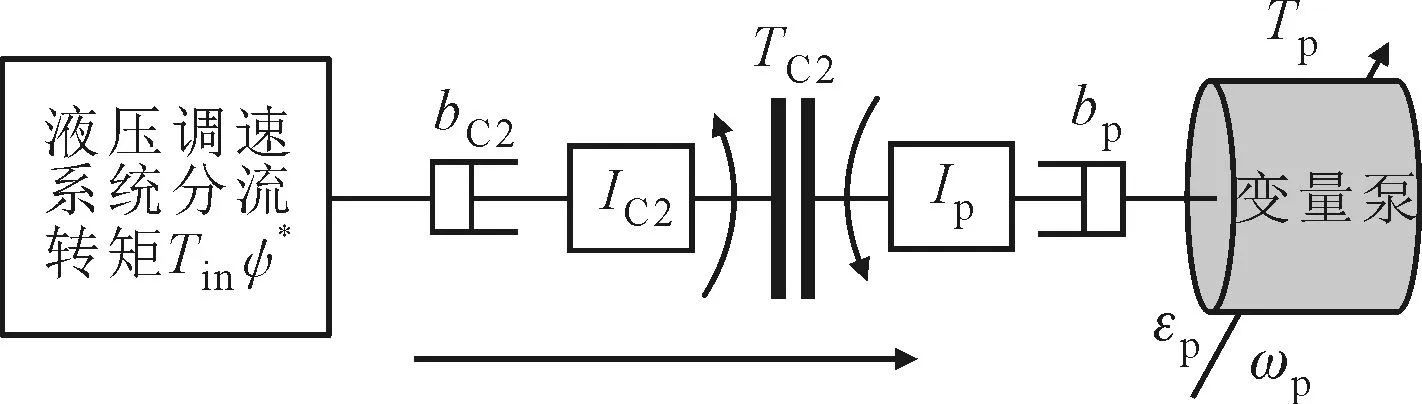
圖5 離合器C2轉矩動力學模型

離合器和變量泵或變量馬達角速度可以通過系統自帶的角速度傳感器進行實時測量,在對變量泵或變量馬達進行補償控制時,將離合器主動盤角速度和變量泵或變量馬達角速度作為狀態變量,把離合器傳遞轉矩作為控制變量,把液壓元件的轉矩的一階導數作為性能泛函,通過狀態反饋來補償離合器傳遞轉矩,以離合器C2控制為例進行分析,轉矩動力學模型如圖5所示。

在離合器C2分離和變量泵排量為0的滑摩階段,可以認為變量泵轉矩Tp=0,那么此時傳動系統的狀態方程可以表示為

(31)

把式(31)轉化為狀態空間的形式為

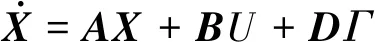
(32)

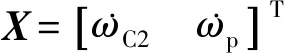
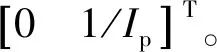
(33)

式中ψ*為液壓調速系統分流轉矩放大系數。

將式(31)代入式(33),整理可得

(34)

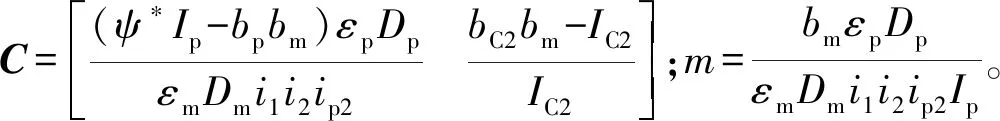
性能泛函為

若取Q=CTC,r=m2,N=mCT,則j可以表示為

(35)

通過求如下的Reccai方程

PA+ATP-(PB+N)r-1(BTP+NT)+Q=0

的解P,得到最優的反饋增益

K=BTP+NT

(36)

由式(36)給出的最優反饋增益矩陣通過變量泵對離合器C2和系統輸出轉矩進行補償,通過求解上述二次型最優控制問題,可求取離合器最優轉矩變化率,進而基于模型求得離合器C2實時傳遞的轉矩。同理,可通過變量馬達對離合器C4傳遞轉矩進行補償。

4 仿真及結果分析

為研究DHMT系統的動力切換特性和控制方法的有效性,利用AMESimMatlab軟件對模式切換過程中的系統輸出轉矩、車速、沖擊度以及滑摩功的變化特性進行仿真驗證及控制性能分析。

4.1 HM1向HM2模式切換過程仿真

DHMT系統的HM1向HM2模式切換時,對系統采用或未采用同步控制的切換過程仿真結果如圖6所示。

由圖6a可以看出,離合器C1向離合器C2進行動力切換的過程中,未對變量泵轉速采用同步補償控制時,變量泵由于離合器C2主動盤擾動影響,出現(-5.5,+7.3) rad/s的角速度差,且穩定調節時間較長,為1 425 ms;對變量泵采用同步補償控制時,二者轉速可在665 ms的時間內達到同步穩定狀態;由圖6b可以看出,對系統采用角速度同步控制后,變量馬達角速度由離合器C3從動盤向離合器C4主動盤的過渡時間減小,說明對液壓調速系統進行轉速同步補償和對切換機構進行轉矩同步補償后可有效降低離合器結合時的滑摩時間,從而縮短HM1向HM2模式的切換時間,從而證明了同步控制方法的有效性。

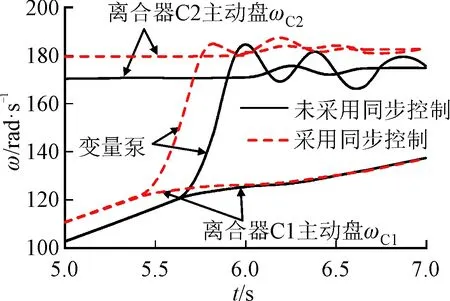
(a)分流模式切換機構角速度

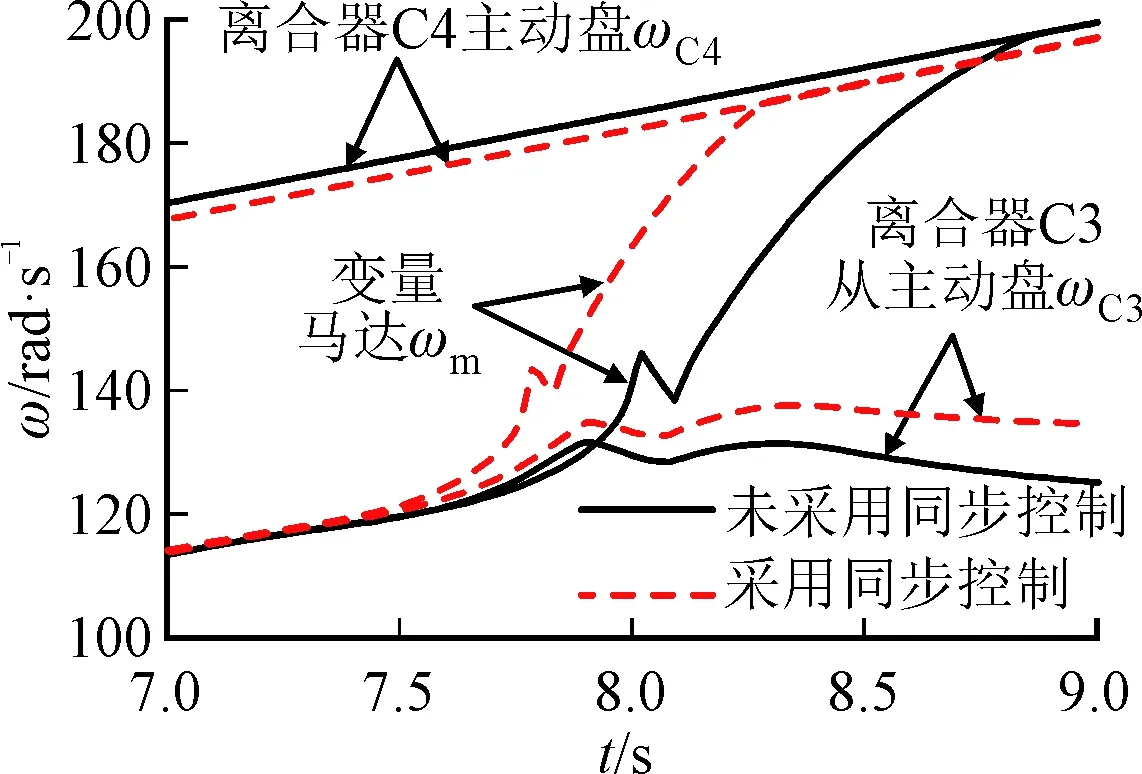
(b)匯流模式切換機構角速度

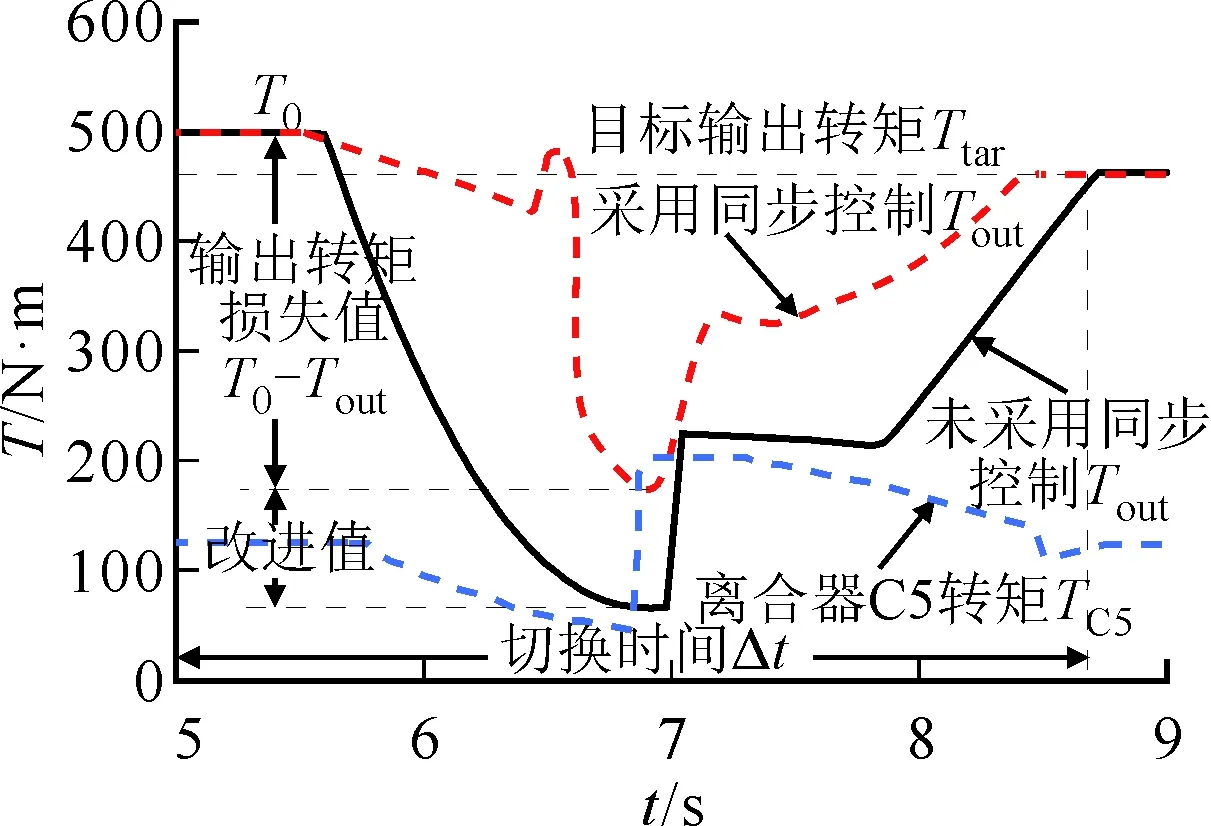
(c)系統轉矩

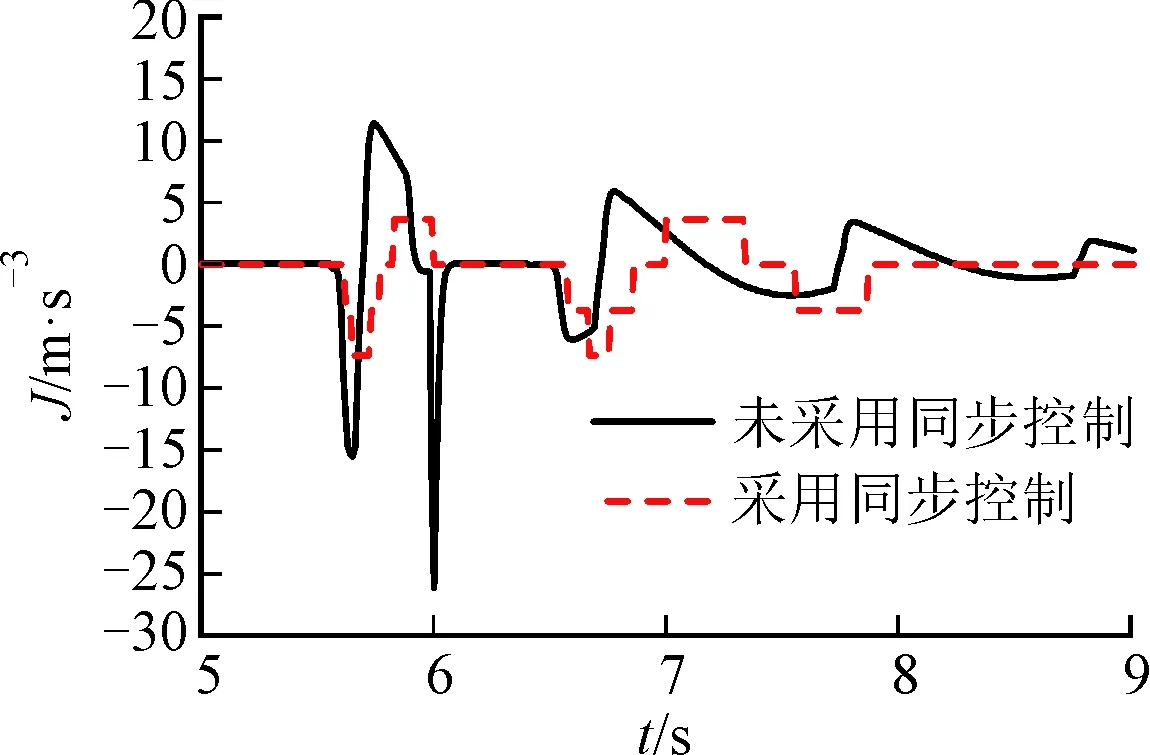
(d)沖擊度

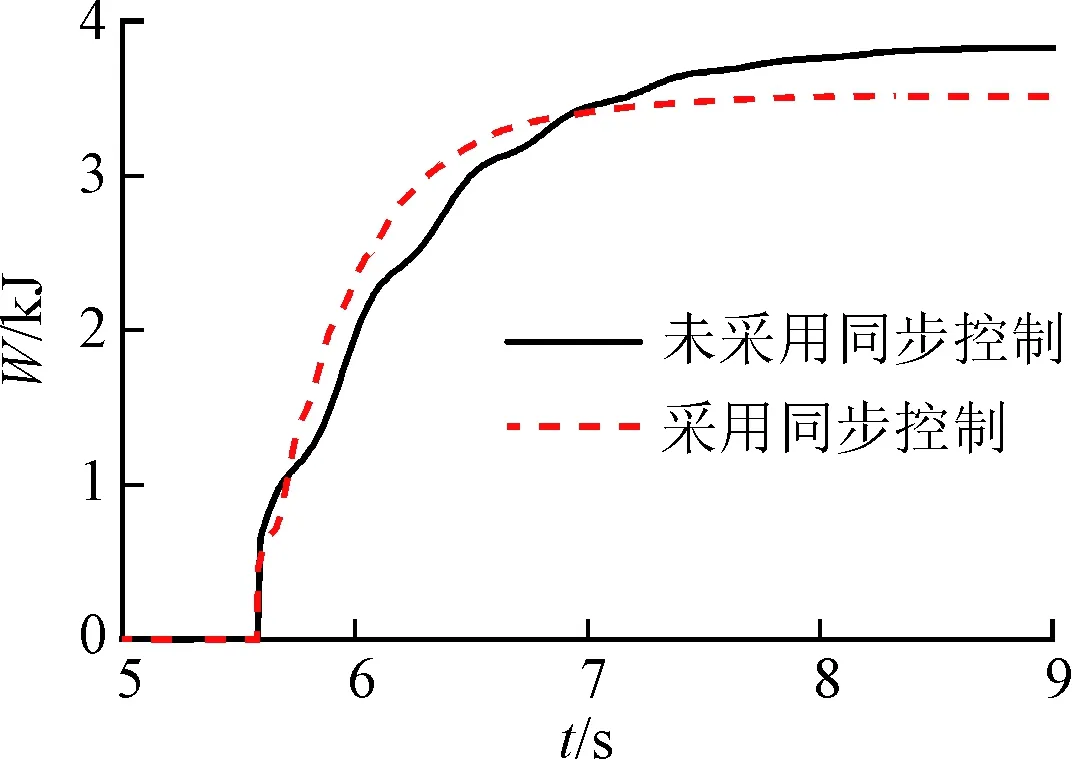
(e)滑摩功

由圖6c可以看出,由于對待結合離合器C2采用角速度同步補償控制和轉矩同步補償控制,從而縮小了離合器主從動盤角速度差存在的持續時間,模式切換過程中,DHMT系統輸出轉矩過渡平滑且損失率降低,相對于未采用同步補償控制的DHMT系統,最大輸出轉矩損失系數降低了28%,切換時間縮短了0.3 s;由于在系統機械功率流輸入慣性力的作用下,7.03 s時離合器C5主從動盤結合,導致DHMT系統輸出轉矩突然增大,從而導致系統模式切換過程平順性較差,對離合器C5采用轉矩同步控制,雖然可有效改善其轉矩變化率,但是并不能消除,因此需要把離合器C5結合時刻的系統轉矩控制在合理范圍之內。

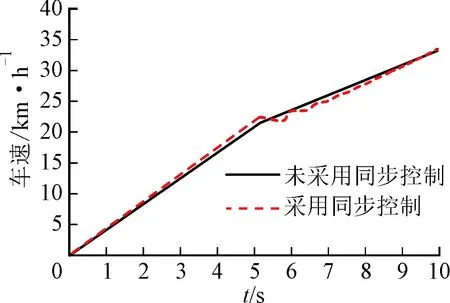
(f)車速圖6 HM1向HM2模式切換過程仿真結果

由圖6d～6f可以看出,未對DHMT系統采用同步補償控制時,在5 s開始驅動模式切換時,整車沖擊度在(-26.8,+12.7) m/s3范圍內波動,而采用同步控制后,則能將車輛沖擊度控制在(-7.2,+5.1) m/s3之間,從而大大提高了模式切換品質。相對于未采用同步控制,采用同步控制對應的滑摩功略有降低,且達到穩定狀態所經歷的時間縮短,這是由于離合器的角速度和轉矩控制不但降低了主從盤的角速度差,而且增大了離合器的實際傳遞轉矩。在DHMT系統由HM1向HM2模式切換時,未進行同步控制時,經過約1.5 s后車速由切換初始車速22.3 km/h逐漸增大至24.7 km/h,在此時間內車速過渡變化平順性差;采用同步控制后,車速在模式切換過程中過渡銜接平順,車輛的動力性有所改善。

4.2 HM2向HM1模式切換過程仿真

由于HM2向HM1模式切換過程與HM1向HM2模式切換過程類似,故針對該過程文中只作簡單仿真分析,而不具體展開討論。HM2向HM1模式切換過程仿真結果如圖7所示。

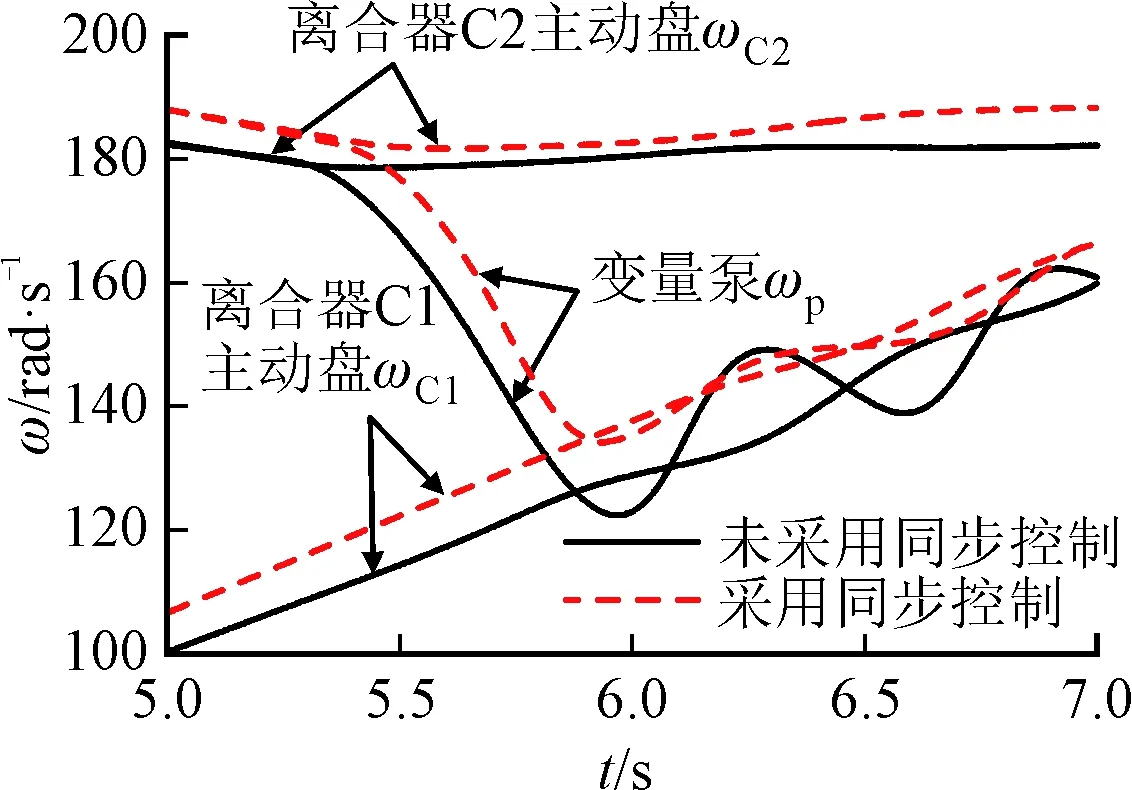
(a)分流模式切換機構角速度

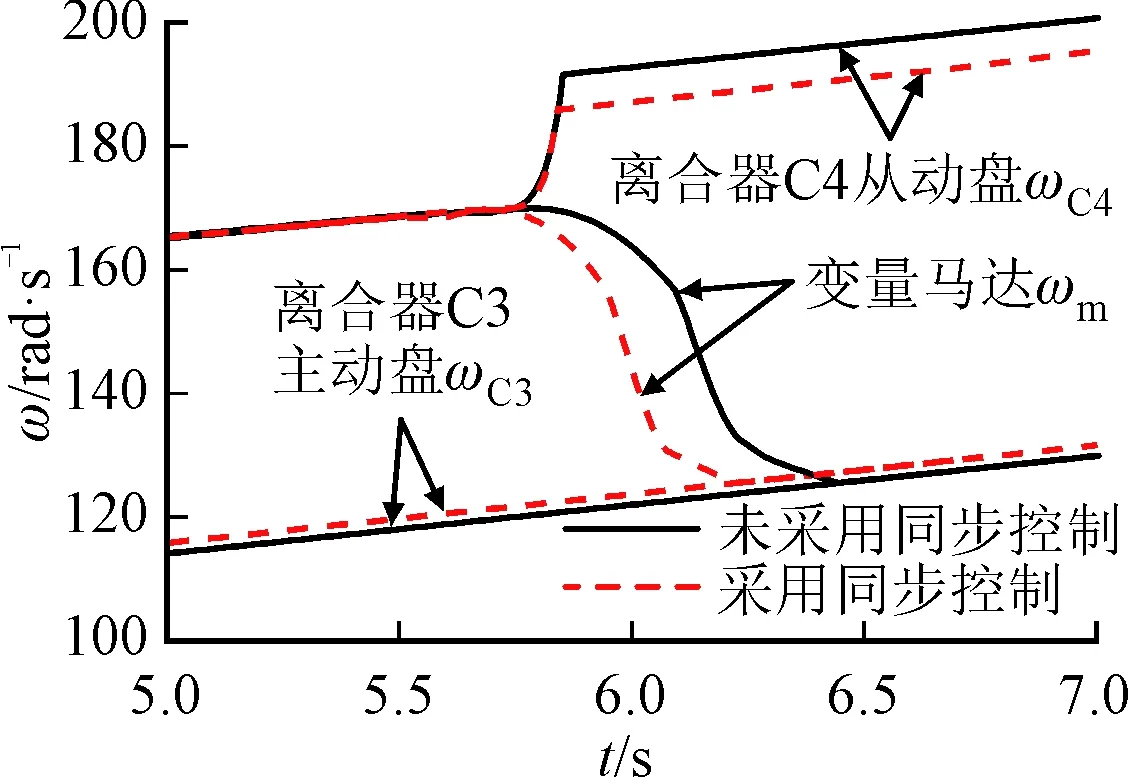
(b)匯流模式切換機構角速度

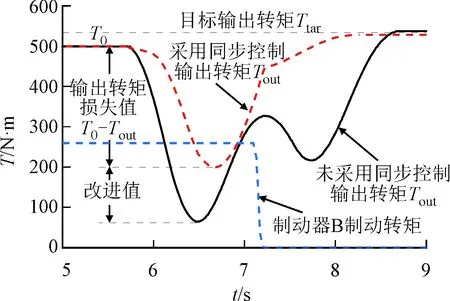
(c)系統轉矩

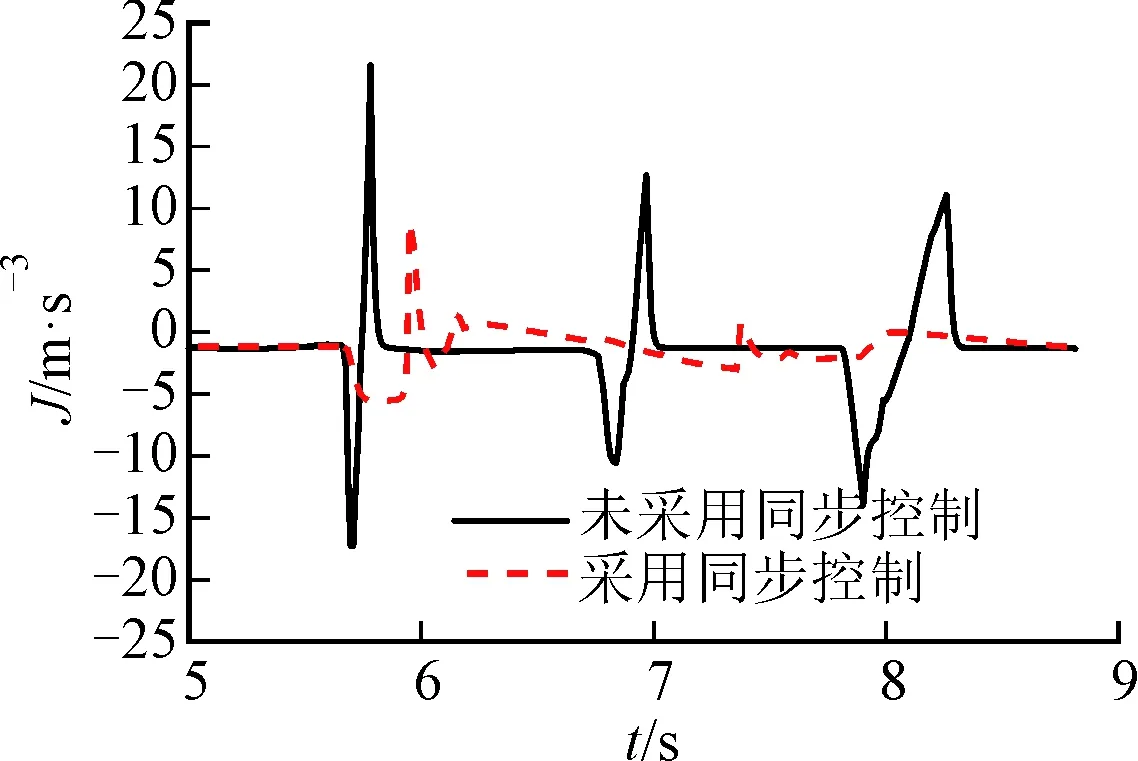
(d)沖擊度

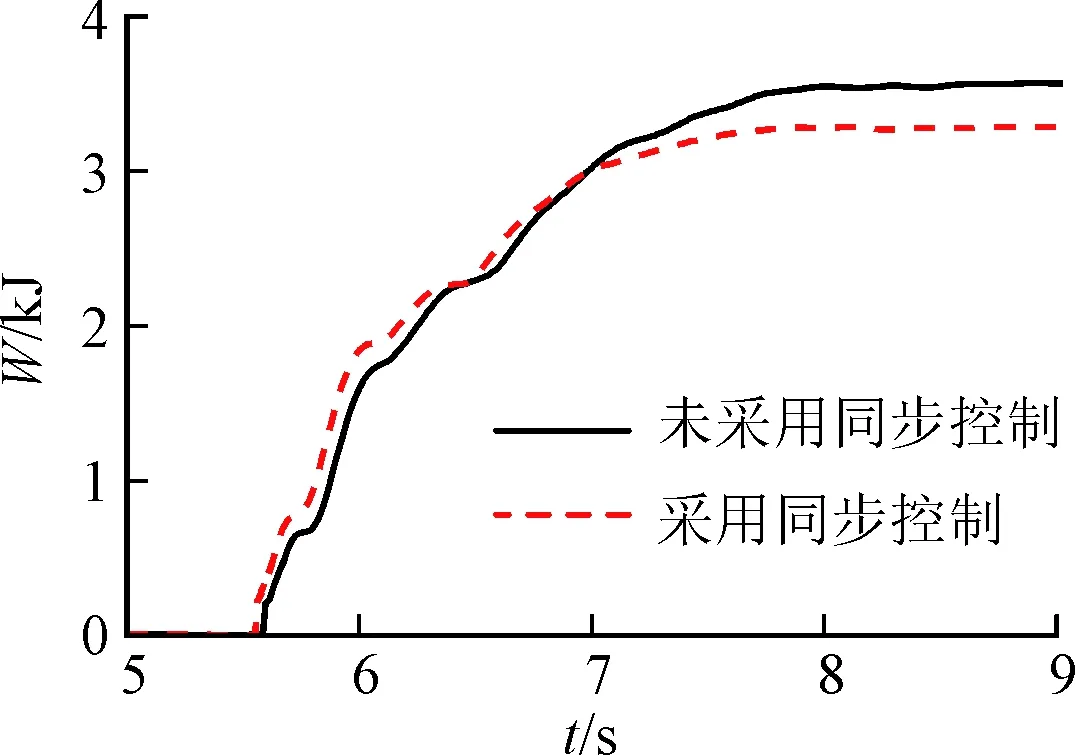
(e)滑摩功

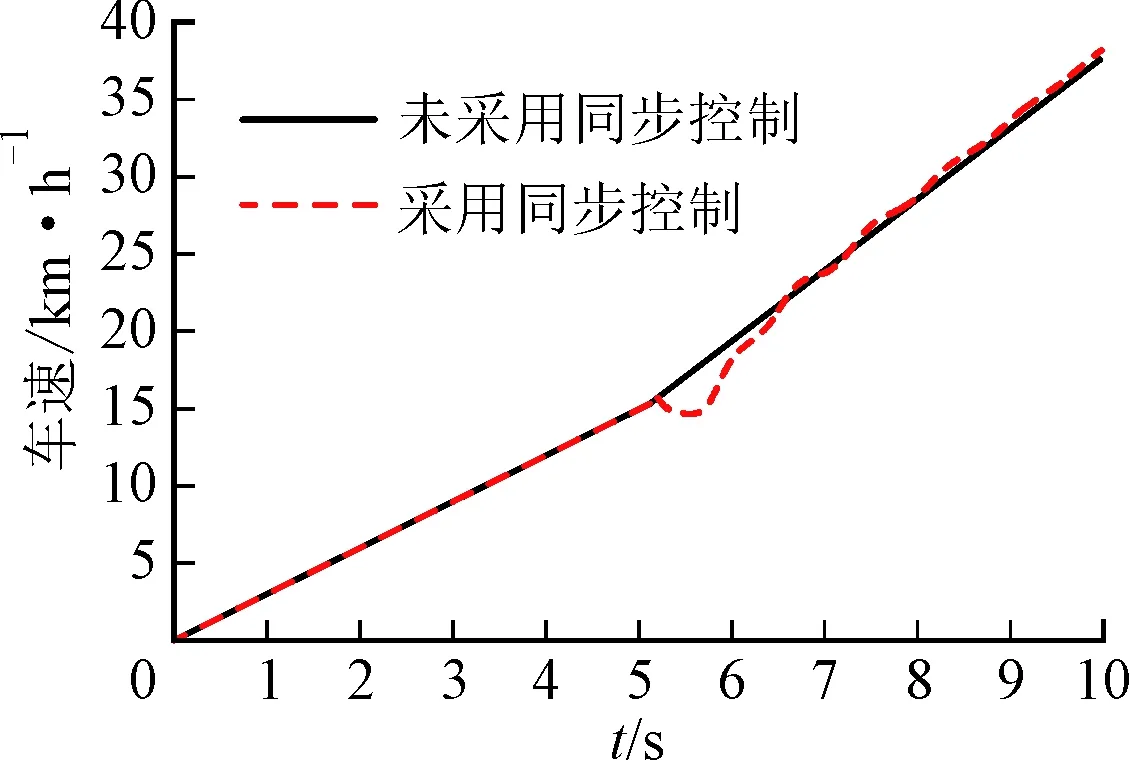
(f)車速圖7 HM2向HM1模式切換過程仿真結果

從圖7a～圖7b可以看出,HM2向HM1模式切換過程中,從5.38 s開始變量泵角速度逐漸從離合器C2過渡到離合器C1,在此過程中,對系統采用同步控制相對于未采用同步控制,變量泵與離合器C1角速度差大大降低,且在6.13 s時二者角速度達到同步,為離合器C1的穩定滑摩結合創造了條件,且變量馬達角速度由離合器C4從動盤向離合器C3主動盤的過渡時間減小;由圖7c～圖7f可以看出,系統最大輸出轉矩損失系數降低了31%,同時沖擊度變化范圍明顯減小,沖擊度變化范圍合理,不會對整車駕駛性能及舒適性造成很大影響。滑摩功較小,完全可以被接受;車速變化比較平穩,換擋平順性較好,由此可以說明同步控制方法對DHMT系統具有一定的控制效果。

5 同步控制實驗驗證

5.1 實驗臺架總體方案

為進一步研究液壓調速系統角速度同步補償控制和切換機構轉矩同步補償控制方法的有效性和正確性,在DHMT系統模式切換實驗臺架上進行了模式切換同步控制實驗,實驗臺架原理和實物分別如圖8和圖9所示。

圖9 DHMT系統實驗臺架

DHMT系統臺架組成包括:驅動電機、DHMT系統、轉矩儀、加載電機以及各種執行裝置控制單元。輸出通過聯軸器與其相鄰裝置連接;驅動電機和加載電機為洛陽合能YVF2-355 M-8型變頻調速三相異步電動機,分別用于模擬發動機與輸出端負載;實驗臺架的控制及信號采集系統主要由一臺工控機、DSP控制器、轉速轉矩測量卡、測量儀表及執行器組成。利用自動代碼生成技術,將Matlab/Simulink中的控制方法模型進行控制器代碼生成,并將其移植到實驗臺架控制器中。

5.2 實驗控制性能分析

對DHMT系統采用或未采用同步控制的HM1向HM2模式切換過程以及HM2向HM1模式切換過程實驗結果分別如圖10和圖11所示。

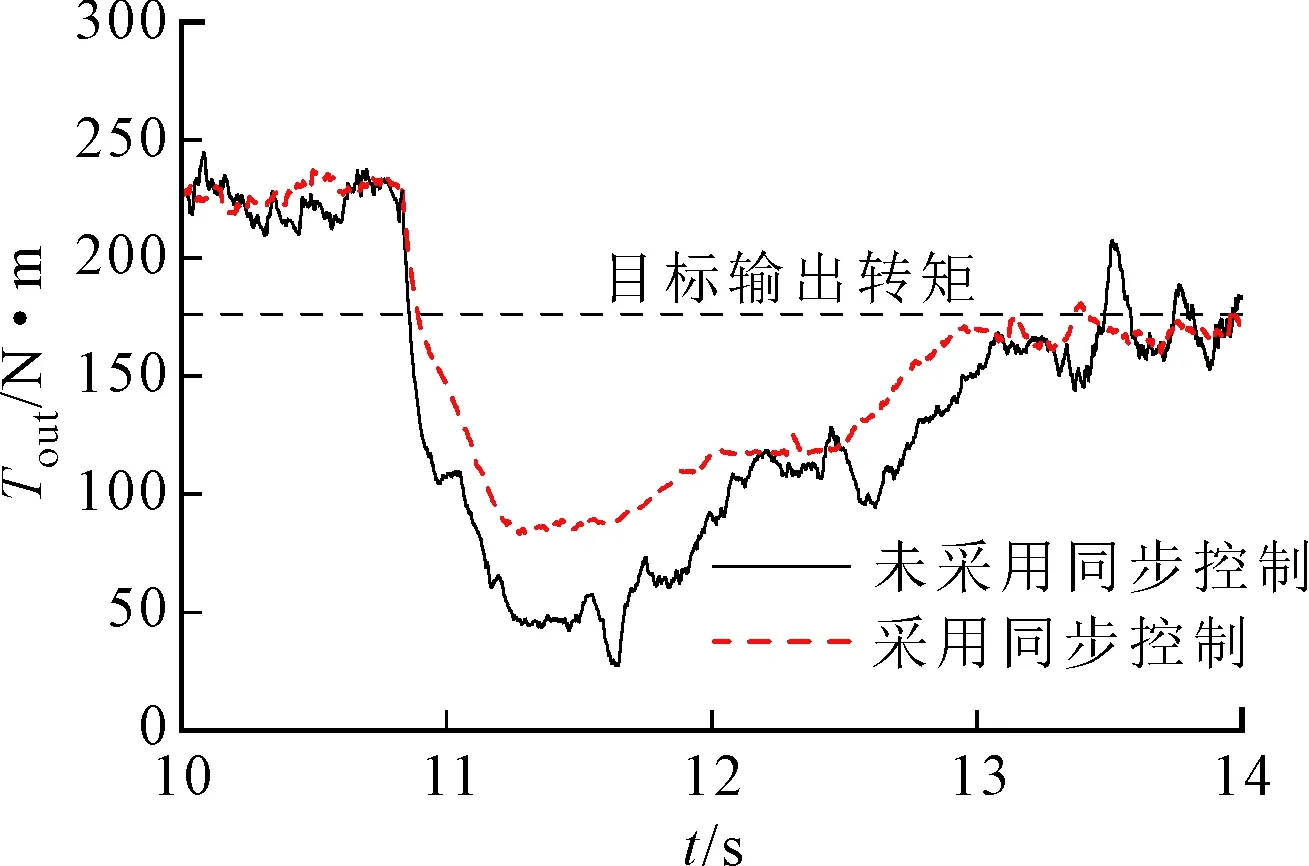
(a)系統輸出轉矩

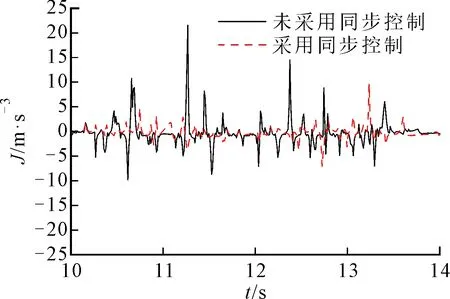
(b)沖擊度

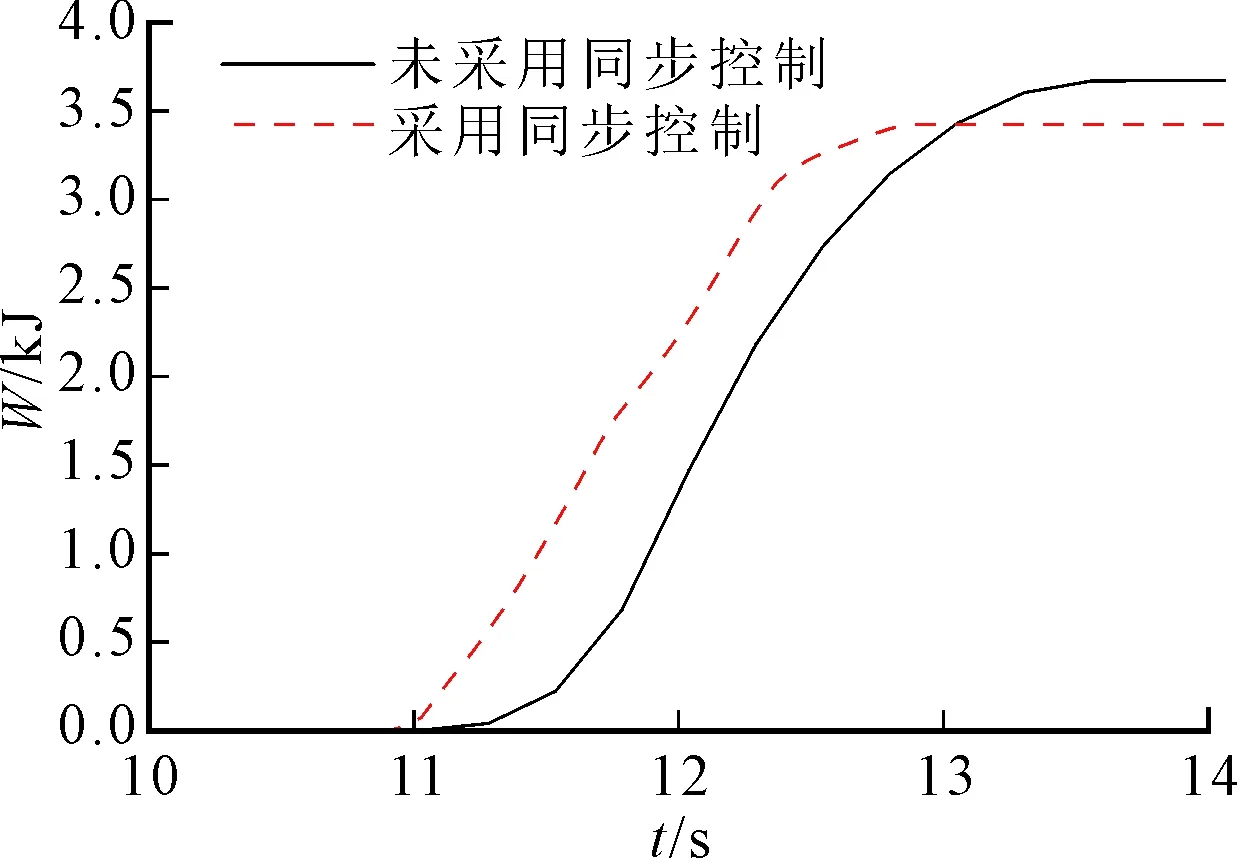
(c)滑摩功圖10 HM1向HM2模式切換過程實驗結果

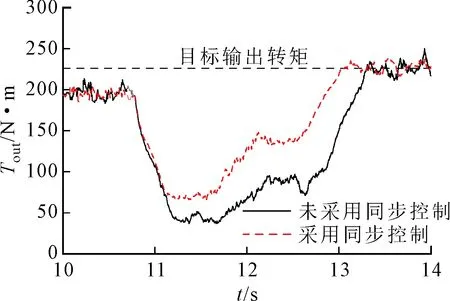
(a)系統輸出轉矩

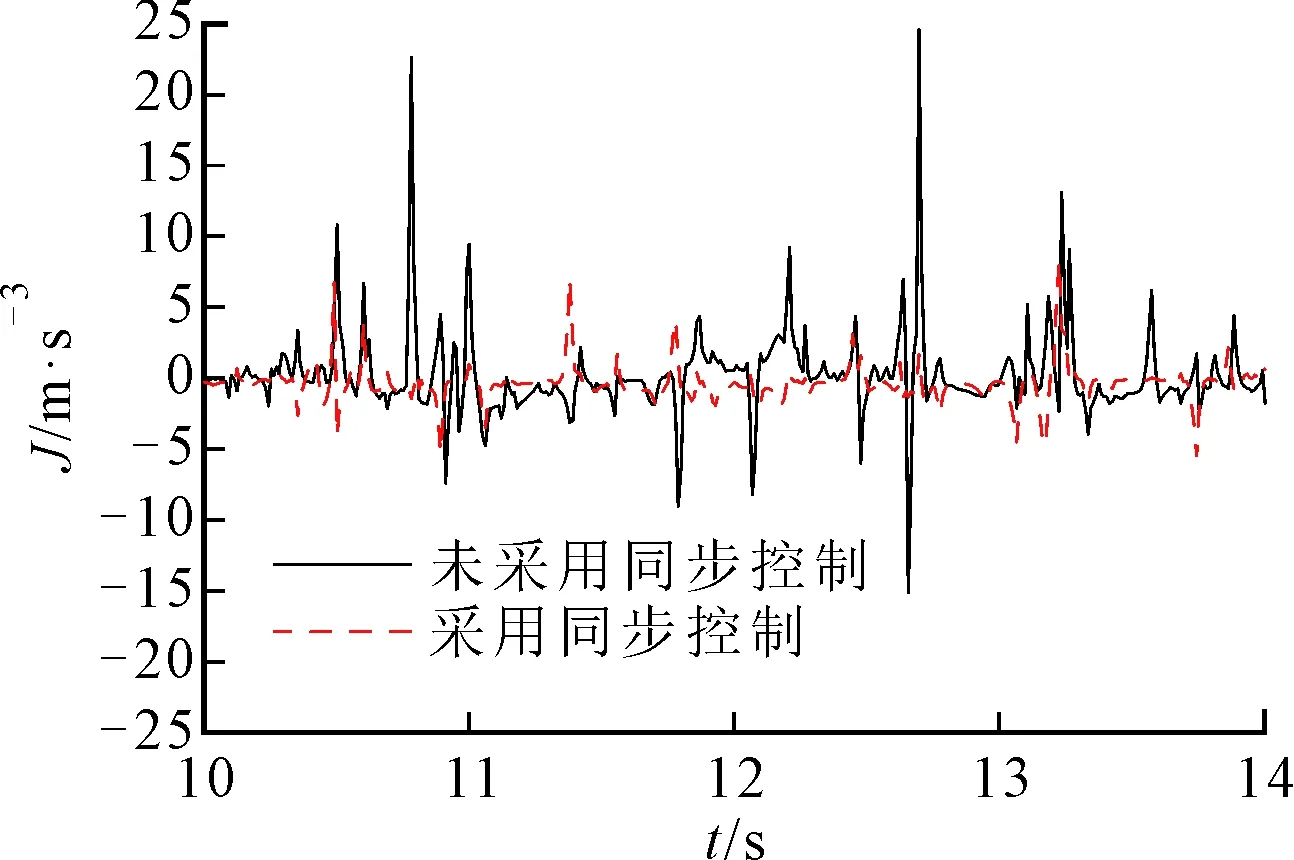
(b)沖擊度

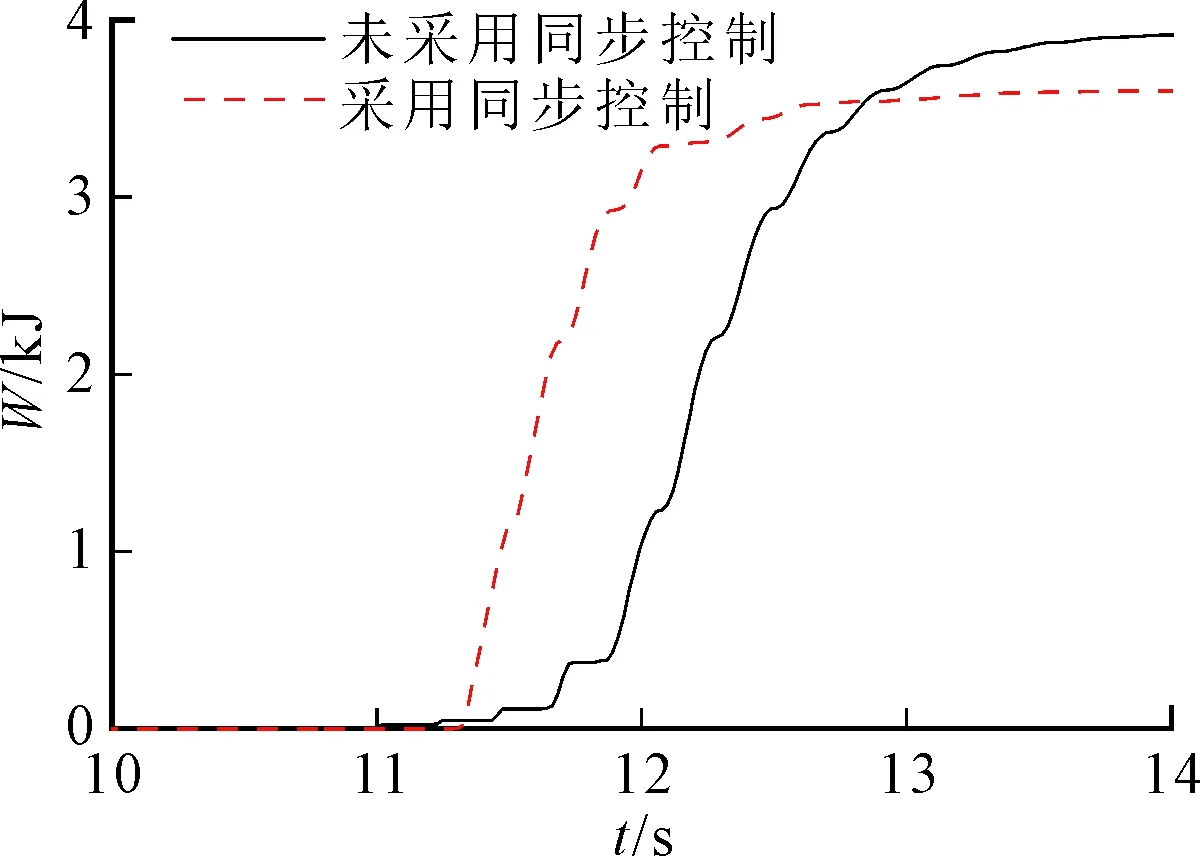
(c)滑摩功圖11 HM2向HM1模式切換過程實驗結果

圖10a為DHMT系統輸出轉矩變化實驗曲線,由圖10a可以看出,與未采用同步控制相比,采用同步控制的HM1向HM2模式切換過程最大輸出轉矩損失系數降低了26.8%,達到穩定輸出轉矩的切換時間縮短了0.42 s,其變化趨勢與仿真環境下的系統輸出轉矩一致,但最大輸出轉矩損失系數出現-1.2%的誤差,切換時間誤差為25%,同時系統輸出轉矩也相對于仿真結果略有降低,出現這種現象是由于液壓系統電比例控制閥組以及管路存在壓力損失以及動作滯后,導致控制系統的精度和靈敏度下降;圖10b為DHMT系統沖擊度實驗曲線,從圖10b可以看出,沖擊度變化范圍明顯減小,控制在(-7.5,+9.8) m/s3之間(等效到車輪上的縱向沖擊度,沖擊度變化范圍規范滿足(-10,+10) m/s3以內),與仿真結果相比,沖擊度控制誤差為16.82%,這是由于離合器C5在結合過程中機械路轉矩突然增大導致,同時HM2模式的速比高于HM1模式,使得切換過程中系統輸出角速度略有增大;圖10c為DHMT系統滑摩功變化實驗曲線,從圖10c中可以看出,滑摩功也相應地減少了0.26 kJ;相對于未采用同步控制的模式切換過程,角速度和轉矩同步控制有效保證了DHMT系統模式切換的平順性,減小了模式切換沖擊和改善了切換性能。

圖11a～圖11c分別為DHMT系統HM2向HM1模式切換過程系統輸出轉矩、沖擊度以及滑摩功變化實驗曲線。由圖11可以看出,對系統采用同步控制,系統輸出轉矩最大損失量降低,并且轉矩降低速率也相對減小,系統動力輸出波動得到有效抑制;但相對于仿真結果系統輸出轉矩波動明顯,這是由于仿真環境下未考慮液壓系統流量脈動的影響。在12.6 s時,對系統未采用同步控制,由于制動器B的制動作用,系統受到負載輸入的反向轉矩出現在-16.3 m/s3的縱向沖擊,加入同步補償后,沖擊度降低為-6.8 m/s3,通過液壓調速系統的角速度同步補償可有效縮短切換機構主從動盤角速度達到統一的時間,同時對DHMT系統輸入角速度擾動進行液壓元件調速補償抑制,從而有效改善了系統模式切換過程中動力中斷問題。

通過以上對DHMT系統模式切換過程的實驗驗證可得,實驗與仿真結果存在一定的誤差,限于實驗本身受多方面因素的影響,但結果都是在可控范圍之內,采用模式切換同步控制方法的實驗結果變化趨勢與仿真相同,可驗證論文建立模型的正確性,從而可以得出該控制方法不僅可以滿足切換品質的各項性能指標,而且能夠有效地解決切換機構的滯后、外界干擾等因素所引起的動力性差等問題,具有一定的魯棒性。模式切換過程實驗結果對比見表2。

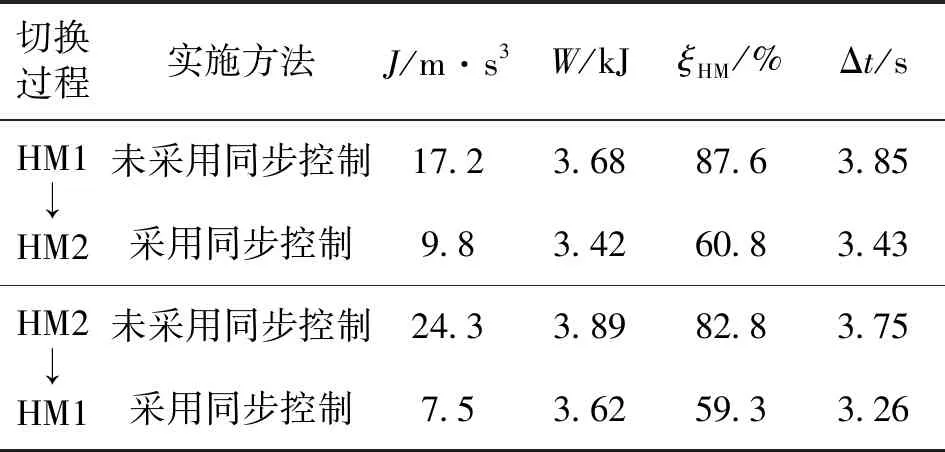
表2 模式切換過程實驗結果對比

6 結 論

本文以雙模式液壓機械復合傳動系統為研究對象,針對其進行模式切換過程中易出現輸出動力中斷及穩定性差的問題,提出了一種基于液壓調速系統轉速同步補償和切換機構轉矩同步補償控制方法。首先,在建立DHMT系統、液壓調速系統以及模式切換機構數學模型的基礎上,對模式切換過程進行3階段理論分析,建立其模式切換各階段動力學約束條件;其次,以系統輸入轉速擾動量作為液壓調速系統角速度同步控制的前饋輸入,從而對液壓元件的轉速波動進行抑制;最后,通過液壓元件轉矩對模式切換機構進行狀態反饋控制,用以消除系統輸入角速度波動導致的切換機構結合轉矩沖擊,從而提高DHMT系統模式切換品質。

模式切換仿真結果表明,本文提出的同步控制方法使DHMT系統HM1向HM2模式切換過程中的最大輸出轉矩損失系數降低了28%,沖擊度控制在(-7.2,+5.1) m/s3的合理范圍之內,切換時間縮短了0.3 s;通過實驗與仿真結果的對比分析,進一步驗證了本文同步控制方法在DHMT系統模式切換過程中具有良好的抗干擾能力和有效性,可大幅度提高模式切換品質,從而為雙模式液壓機械復合傳動系統的設計與研究提供理論參考。