基于應變軟化模型的軟巖巷道卸壓孔布置

趙韋韋

(山西潞安集團 慈林山煤業有限公司， 山西 長治 046605)

0 引言

在煤礦生產中，隨著開采深度的增加，復雜的地質條件使得高應力、高圍壓的巖石巷道越來越多，沖擊地壓災害常有發生，此種情況嚴重影響我國煤炭的正常開采并帶來一定的安全問題。目前，多種釋放高應力的手段被應用于礦井生產，其中大直徑鉆孔卸壓技術的應用效果明顯，并且應用成本較低，被廣泛使用[1]。鉆孔卸壓技術使得巷道的應力峰值向巷道圍巖的深部轉移，降低了所處圍巖的應力狀態，有效防止了圍巖沖擊地壓的發生[2-3]。本文采用考慮應變軟化的摩爾庫倫準則計算分析巷道圍巖軟化區范圍，并以此為基礎作為現場設計卸壓鉆孔間距的理論依據。

1 工程地質背景

山西潞安集團慈林山煤礦的高應力巷道開挖過程中，伴隨著極其強烈的沖擊地壓發生，對生產造成嚴重影響，對工人生命安全帶來嚴重威脅。因構成巷道的巖石巖性多為軟巖，進行支護的效果并不顯著，且支護成本及維護的費用較高，所以對礦山的經濟發展造成了較大的阻礙。為解決巷道圍巖的應力集中問題，決定采用大直徑鉆孔卸壓方法,如何最優化布置大直徑鉆孔間距影響到卸壓效果的好壞以及卸壓成本的高低，為得到有效且合理的卸壓孔布置方案，本文以應變軟化下的塑性區大小為依據確定卸壓孔間距。

2 理論分析

2.1 力學模型

本文采用考慮應變軟化的摩爾庫倫準則[4-6]，該準則所使用的力學模型由圖1所示。

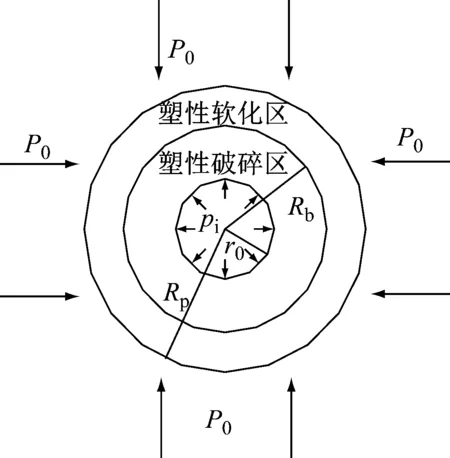
圖1 考慮應變軟化的摩爾庫倫準則力學模型

圖1中,P0為原巖應力；設巷道斷面為圓形，其圓形半徑為r0；在巷道徑向方向產生了塑性破碎區Rb與塑性軟化區Rp。由圖1可以看出,所劃分的2個開挖影響區域由內而外分別定義為塑性破碎區、塑性軟化區。2個區域分別代表著圍巖處于塑性軟化狀態和殘余應力狀態。計算時僅考慮塑性軟化區的范圍大小，不考慮塑性破碎區。

2.2 屈服準則

假設鉆孔處于靜水應力場，且不考慮圍壓不等，該問題屬于軸對稱問題。構成巷道的圍巖具有各向同性且均質。假設巷道軸向長度無限，簡化為平面應變問題。

摩爾庫倫屈服準則在塑性區的表達為：

(1)

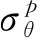
3 鉆孔應力分布狀態及影響范圍

在側壓系數為1的條件下，塑性軟化區總應變：

(2)

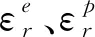
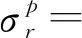
(3)

(4)

式中：σc為巖石的單軸抗壓強度；Mc為巖石的軟化模量，可由應力等值于殘余強度的差值和最大、最小主應變的差值相比求得；η1為系數,取值上可與KP取同值。

當圍巖處于塑性狀態時：

可得塑性軟化區半徑表達式為:

(5)

4 數值模擬分析

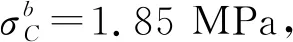
由圖2看出,隨著與巷道壁距離的逐漸增加，巷道徑向方向的切向應力先增大后減小，在與距離巷道壁10 m時的最大應力為14.5 MPa，應力集中系數為1.45，在距離巷道壁30 m時應力減小為原巖應力。巷道徑向方向的徑向應力逐漸增大，在距離巷道壁30 m時，增大到原巖應力。

圓形巷道圍巖中的切向應力可以視為巷道垂直應力[3]。提取圖2中按巷道徑向方向各點的切向應力，得表1。以鉆孔深度為基準，按照求得開挖巷道的塑性圈大小的方法，可以得出不同深度下鉆孔所對應的應力值，即表1所示。

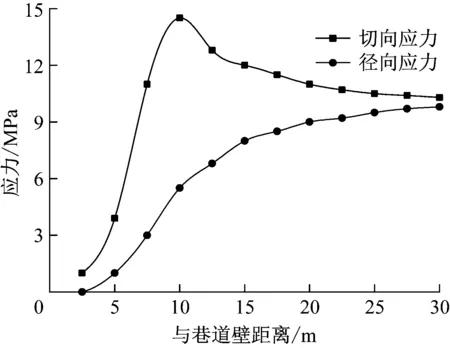
圖2 開挖巷道的徑向與切向應力變化曲線表1 按巷道徑向方向各點切向應力

與巷道壁距離/m124681012應力/MPa1.11.33.14.612.814.513.2

以表1所得的鉆孔軸向(即沿巷道徑向方向)各個點的切向應力大小為基礎，將求得的鉆孔各點的截面作為新的圓形截面，分別求截面的塑性區大小，并以塑性軟化區的邊界作為鉆孔的影響范圍，以表1各個點所對應的影響范圍為判斷依據，將表1對應的切向應力作為鉆孔各個點計算其塑性區大小的原巖應力，代入式(5)，得出鉆孔各個點的塑性軟化區影響半徑，見表2。

表2 沿鉆孔軸向卸壓范圍與變形量

由表2可知：各個鉆孔各個點的影響范圍大小，最大影響范圍為0.51 m，將此范圍作為鉆孔的最大影響范圍，并以此為基礎布置鉆孔可得出鉆孔的布置間距在1 m時，不同鉆孔之間可以相互影響達到卸壓的目的。

巖石的黏聚力反映了巖石本身的性質，根據上述鉆孔卸壓的相關數據，運用MATLAB進行了巖石黏聚力的數值模擬，見圖3。

由圖3看出，在軟巖巷道的塑性區范圍內，進行鉆孔卸壓的巷道在其巷道的徑向方向黏聚力減少，使得巷道內壁上的聚集的巖石能量隨著巖石的破碎釋放，且在巷道內壁上形成塑性區，一定程度上阻滯了力的傳遞。

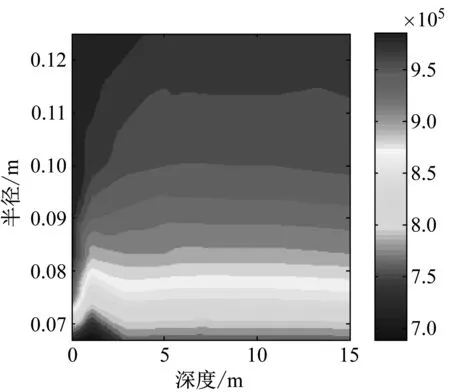
圖3 鉆孔影響范圍內巖石黏聚力變化

5 結論

1) 應用MATLAB模擬了以應變軟化模型為基礎并考慮擴容影響下的巷道和鉆孔應力分布情況，得出結論：卸壓孔布置間距為1.0 m可以達到較好的卸壓效果。

2) 卸壓孔在巷道周圍形成一定寬度的塑性軟化區，使得巷道周圍的能量在釋放時受到一定程度的阻滯，衰減了應力作用。