基于BP回歸神經網絡的人體角度擬合研究①

王景中， 胡 凱

(北方工業大學 計算機學院，北京 100144)

1 引言

人體動作識別存在著廣泛應用，比如視頻監控、客戶的屬性分析、行為分析. 比較流行的人體動作識別方法，主要分為兩種，一種基于卷積神經網絡.2013年余凱提出3D卷積神經網[1，2]，其通過將連續的7幀60×40圖像數據送入卷積神經網絡中進行訓練，通過將卷積核提取的特征進行堆疊形成3D卷積核，進而實現人體行為識別. 2014年由Karen Simonyan等人提出雙流卷積神經網絡[3，4]，結合VGGnet、GOOGLEnet等深度學習模型對視頻中人的連續動作提取光流特征，再將光流特征與原始圖像送入卷積神經網絡中進行訓練，從而實現動作識別. 2018年由 Zisserman A等人提出的I3D[5]模型是將上述兩種放法進行結合. 另外一種方法為基于深度攝像機[6，7]，它除了能提供人體的骨骼特征之外，還能夠提供人體的相對深度信息，即輸出的數據為(x，y，z)，分別代表骨骼點在圖像中的坐標及深度信息，然后結合支持向量機(SVM)[6]、隱馬爾可夫模型(HMM)[7，8]等機器學習方法既可以對人體的動作進行有效識別.

雖然上述方法均能實現對人體動作的識別，但是其應用也有一定的局限性. 基于卷積神經網絡的識別方法，只能對動作進行分類，不能給出人體姿態的其它相關信息; 對于訓練數據和被識別數據必須是由連續動作組成的圖像，當動作不連續時，則不能進行有效分析. 基于深度攝像機的識別方法，雖然能較好的完成人體動作識別，但對視頻中快變場景或者靜態圖像無法完成人體動作識別.

本文中分析對象為普通視頻中人的動作，視頻中圖像的特點為場景變化快、圖像中的人物動作多變且不連續. 通過以上分析可以看出，上述方法均不能應用于這種應用場景.

近年來，隨著人體姿態估計方法不斷發展，其已經具有很高的識別精度. 2016年由卡內基梅隆大學Cao Z、Simon T等人提出的openpose框架[9，10]，其使用卷積神經網絡和PAF算法實現人體姿態估計. 另外，2017年由上海交通大學盧策吾等人提出RMPE框架[11]，其使用對稱空間變換網絡(SSTN)、參數非最大化抑制(PNMS)等方法實現對多人人體骨骼框架的提取. 本文中定義被擬合角度的坐標空間后，利用openpose框架提取出人體骨骼特征數據，經過數據重構、預處理及增加肢體相關的先驗信息，生成10個與人體角度相關的數據集. 使用基于“徑向基核(RBF)”的SVR[12]回歸模型作為基線，與BP神經網絡的回歸[13，14]結果做比較.另外通過主成分分析(PCA)[15，16]方法計算標準數據集和增維后數據集特征值，通過特征值的方差證明增維數據的有效性. 通過分析實驗結果，使用加入先驗信息的數據集，4層BP神經網絡訓練結果要優于基于RBF核SVR回歸模型的訓練結果，數據集增維后，數據間的關聯有效減小.

2 靜態圖像人體角度擬合

2.1 骨骼數據提取

使用openpose框架對人體骨骼關節點數據進行提取，骨骼示意圖如圖1所示. 本文中只對人體相對于攝像機的正面、左側面和右側面時的人體手臂關節角度進行擬合，提取的骨骼數據包括：頸部、左肩膀、左手肘、左手腕、右肩膀、右手肘、右手腕、髖關節，對應的編號分別為：1、2、3、4、5、6、7、8.

圖1 人體骨骼特征編號示意圖

2.2 數據定義

本文中將人體骨骼以頸部為中心分為左右2個部分，通過分析人體動作特征，每半個部分只要確定4個自由度即可確定相應的動作姿態，所以共需要對8個角度進行擬合，角度左右對稱. 相關數據定義以及需要擬合的角度定義見表1.

表1 相關數據對照

2.3 構建數據集

由于沒有人體角度相關的標準數據集，本文中所使用的數據集，均為自行設計. 生成的數據集見表2. 相對于8個被擬合的人體角度，共生成6組數據集，對應表1中定義的角度. 6組數據中細分為5個標簽，分別對應一個被擬合角度空間的不同狀態，分別為∠10、∠45、∠90、∠135、∠180，其中角度Ar2和Ar3共用一組數據、其中角度Al2和Al3共用一組數據，每組數據1000張照片，其中訓練集比例為80%，測試集比例為20%. 訓練數據見圖2.

表2 生成的數據集

圖2 訓練數據

提取出相應的骨骼數據后，為了保證訓練數據的相對位置不變性，首先將數據集變換到同一坐標原點，本文中以頸部作為人體坐標中心，計算方法為：

為了保證數據的尺度不變性，需要對數據進行歸一化處理，計算方法為：

通過觀察人體骨骼特征，若不考慮觀測角度，人體大臂和小臂的長度約為軀干的0.5倍左右，為了提高角度擬合的精度，對上述部分數據集加入手臂長度的先驗信息，提高數據集維度，文中設定手臂與軀干的比例系數為0.6. 計算公式為(3). 重新構建數據集，將對應同一角度的兩套數據集在不同的模型中的擬合結果進行比較.

2.4 主成分分析方法

通過主成分分析(PCA)方法，對增維的數據集和正常數據集進行分析，PCA計算過程如下：

計算數據集的協方差矩陣：

計算協方差矩陣的特征值和特征向量：

在得到特征值矩陣后，計算特征值矩陣中特征值的期望和方差并比較不同數據集的計算結果.

2.5 BP神經網絡模型

BP神經網絡由輸入層、隱層和輸出層組成. 其通過有監督學習方式進行訓練，即在訓練時需要一定數量的有標簽數據. 通過訓練數據的正向傳播得到訓練誤差，通過誤差的反向傳播修正神經元的權重. 本文中構建的所有神經網絡均為4層，其中隱層h1和h2的神經元數量為50和32，激活函數選擇為Sigmod函數，見式(7)～式(8)，輸出層神經元個數為1，激活函數為線性函數，見式(9)，學習率α設置為0.1，訓練次數為650 000次.

當BP神經網絡處于正向傳播時，輸入數據由輸入層通過隱層最終到達輸出層，其計算公式為：

當BP神經網絡進行反向傳播時，其使用隨機梯度下降進行優化，本文中BP回歸神經網絡的損失函數定義為：

通過上式不難看出，優化的過程即是對二次函數尋找極小值點的過程. 如圖3.

圖3 非凸二次函數示意圖

若二次函數為非凸函數，在訓練過程中，若參數選擇不合理，BP神經網絡會將局部極小值點[13，14]作為全局極小值點作為優化的目標，為了避免這種情況，本文中使用批量訓練(minibatch)的方法進行訓練，batchsize設置為40.

BP神經網絡在反向傳播時，通過求各個層中的偏導數獲得權重的優化方向后，通過公式(12)～(13)對權重進行修改，其中w 為神經元權重、b 為神經元偏置.

由于均為復合函數，其梯度值計算為式(14)～式(15)：

2.6 性能指標評估

對于擬合結果指標評估的方法包括：“平均絕對誤差(MAE)”、“平方誤差(MSE)”以及“R平方值(RSquared)”，本文中采用MAE作為歸回結果性能評估指標之一，公式為式(16). 另外，允許擬合的結果產生一定的誤差，MAE指標評估了所有訓練數據的誤差，并不能準確的反應回歸的精度，所以本文中使用分類指標評估思想，對AUC[16]指標進了修改，其中T為正確樣本數量、U為樣本總數量，通過設定不同的err值確認回歸結果的精度范圍，公式為式(17).

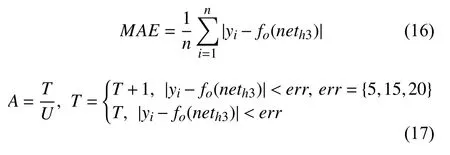
3 實驗測試分析

為了對比BP神經網絡擬合結果的性能，使用了SVR回歸模型的訓練結果作為基線，該模型可以設置核函數，分別為“線性核(linear-kernel)”、“徑向基核(RBFkernel)”、“多項式核(ploy-kernel)”. 其中“線性核”函數不具備非線性空間擬合的能力，“多項式核”在多維數據下訓練時間比較長，所以在這里選用“徑向基核”作為SVR的核函數，開發工具使用sklearn. 詳細參數設置見表3.

表3 SVR回歸模型參數設置

針對上述內容，共設計4組實驗，為了避免重復說明，這里只對人體骨骼右臂的Ar1角度的擬合結果進行詳細說明，對于其它數據集直接給出實驗結果，實驗設計見表4.

實驗過程中，每1000次迭代記錄一次訓練集損失數據和測試集損失數據，分析模型的損失函數曲線，實驗C4效果最好，訓練集數據的損失和測試集數據的損失均為最小，分別為0.1314(紅色實線)、0.1933(藍色虛線); 實驗C1效果最差，訓練集數據的損失和測試集數據的損失均為最大，分別為0.5275(紅色實線)、1.030(藍色虛線). 詳細實驗訓練曲線見圖4～圖7.

表4 實驗設計

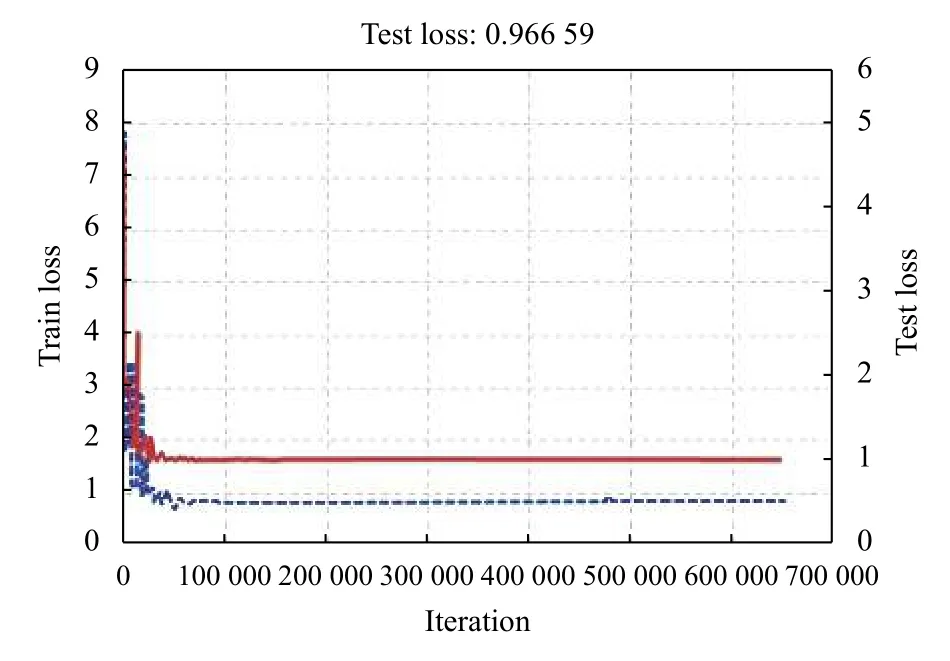
圖4 實驗C1損失函數曲線

圖5 實驗C2損失函數曲線

圖6 實驗C3損失函數曲線

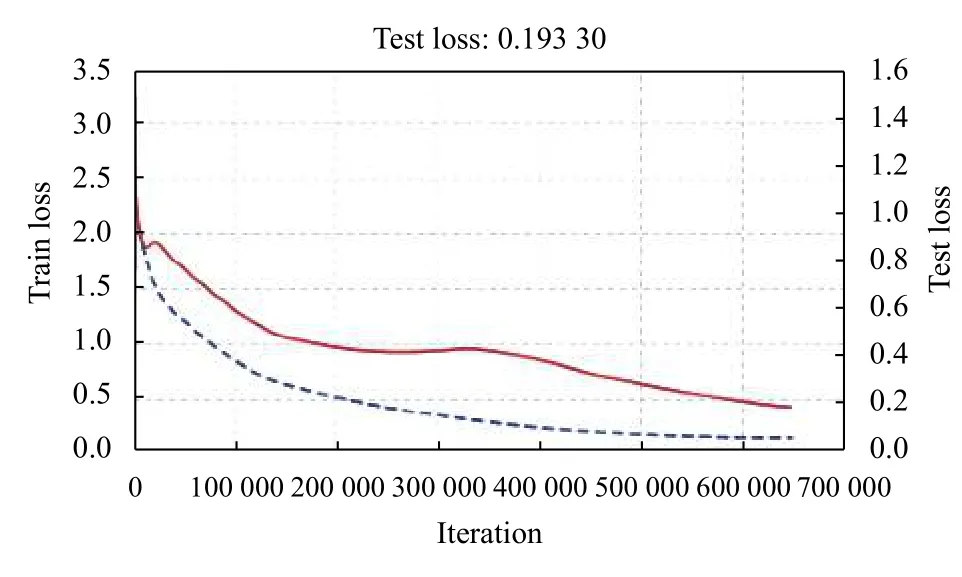
圖7 實驗C4損失函數曲線

使用BP回歸神經網絡，通過數據集T3、T6、T8、T10，對人體其它7個角度進行回歸訓練，各項指標見表5. 實驗結果見表6.

表5 Ar1角度擬合實驗結果

對于增維數據的有效性，通過PCA方法對數據集進行分析，計算各數據的特征值的方差，計算結果見表7.通過分析結果看出增維后的數據集方差更小，說明數據集增維后的數據集相比較標準數據集可以有效減少數據的關聯性.

4 實驗結論

本文在定義了人體相關角度空間的情況下，提出利用openpose提取人體骨骼數據，經過數據重構、預處理以及升維后，生成訓練數據集，通過BP回歸神經網絡對人體相關的8個角度進行擬合. 通過對比試驗結果及相關的指標表明，該方法可以有效的擬合出對應的角度，為動作識別提供依據. 雖然卷積神經網絡經過大樣本訓練后會有更強的表達能力，但其只是對數據整體進行評估，更適用于整體分類，不能給出分類結果的相關細節的信息. 若要使用單一的卷積神經網絡對人體的動作進行分析，需要對被訓練數據的各個部分進行非常精確的標注，考慮到圖像中的觀測視角和人的身體動作均為變量，此項工作量巨大. 使用文獻[1-5]中提出的方法將卷積神經網絡和光流特征結合完成動作識別，但對圖像連續性有一定的要求，并且不能給出人體肢體動作的局部信息. 基于以上原因使用BP回歸神經網絡并結合提取的骨骼數據的方法，可以更好的完成人體動作角度識別. 下一步考慮將與深度置信網絡(DBN)相結合，進一步提高其擬合的精度.

表6 其它角度擬合實驗結果

表7 數據集的方差對比