基于局部能量的邊緣檢測方法①

潘園園， 曾笑云， 劉 洋， 楊晟院， 左國才

1(湘潭大學 信息工程學院，湘潭 411105)

2(湖南軟件職業學院 軟件與信息工程學院，湘潭 411100)

邊緣是像素灰度值發生劇烈變化的像素的集合，圖像大部分的信息存在于邊緣中. 邊緣檢測是圖像處理領域中研究最廣泛最重要的課題之一，也是圖像分割、圖像重建、特征提取和目標識別的基礎.

當從圖像中提取邊緣時，通常會出現一些錯誤，比如曲線不連接、缺失邊緣和假邊. 因此，構建一種能夠精確檢測圖像邊緣的方法是至關重要的. 目前為止，已經有許多不同的方法成功的應用到圖像邊緣檢測中[1-6].文獻[1]提出一種在邊緣檢測過程中加入邊緣曲度算子進行噪聲衰減的邊緣檢測方法. 此方法可以抑制噪聲得到較高的定位精度，但耗時比傳統Canny方法有一定的增加. 文獻[2]是采用小波變換和改進的自適應中值濾波器代替Canny方法中使用的高斯濾波器對圖像進行平滑處理，具有較高的定位精度，但時間復雜性有所增加. 文獻[3]提出了一種基于灰度關聯的自適應邊緣檢測方法，該方法可以自適應的計算閾值，使邊緣更加完整，但有時沒有設置閾值精度高. 文獻[4]提出了一種基于估計理論的邊緣檢測方法，該方法在局部細節上具有一定的優勢，但檢測完整性不具有優勢. 文獻[5]提出一種Canny算子與智能路由算法相結合的邊緣檢測方法，該方法對邊緣映射效果要求很高. 文獻[6]提出一種基于多級形態學的模糊邊緣檢測方法，該方法可以得到較準確的邊緣檢測結果，此方法適用于有多目標而不是單一目標.

目前已有的邊緣檢測方法除了對傳統邊緣檢測算子進行改進之外，隨著人工智能的發展，又出現一些新的邊緣檢測方法[7-10].

從數學角度分析，微分要求函數曲線具有一定的光滑度，但積分對函數曲線的光滑度要求不高. 因此，本文從積分的角度，提出一種基于局部能量的邊緣檢測方法. 此方法是在以一個像素點為中心的對稱區域中，計算區域內所有像素的灰度值與中心像素的灰度值之間的差值，差值平方的總和作為中心像素點所對應的局部能量. 這個局部能量是一種積分形式的. 通過局部能量的大小來判斷此積分區域內是否存在邊緣.一般地，邊緣點對應的局部能量較大，而光滑區域內的像素點對應的局部能量是比較小的. 因此，根據局部能量函數的大小，就可以快速有效地找到邊緣點所在的位置.

1 基于局部能量的邊緣檢測方法

1.1 局部能量方法

圖1(a)是一個理想的階躍曲線，灰度值的躍變表成一個集合，像素點y∈Ωx，f(x)是中心點x的像素灰度明圖像中邊緣點的存在. 圖1(b)是階躍曲線的導數.圖1(b)中的峰值點對應圖像的邊緣點. 如圖2所示，假設有一條線段L，長度是2r，線段的中心點是x. 讓線段L的中心點沿著曲線移動. 運動過程如圖2所示. 中心點x在曲線上移動過程中相對應點的像素灰度值都稱為f(x)，而線段與曲線所圍對稱區域內所有像素點構值，f(y)是對稱區域內其他像素點y的像素灰度值. 計算此對稱區域內所有像素灰度值f(y)和中心點x的像素灰度值f(x)的差值平方和，這些差值平方和稱為中心像素點x所對應的局部能量.

圖1 階躍曲線及其導數

圖2 水平線段L的中心點沿曲線運動時，曲線與水平線段L的中點的差值示意圖

根據以上的分析，局部能量函數定義如下：

考慮到高斯核函數K(x)具有緊支撐性和加權的特性，式(1)可以改寫成：

本文選擇的高斯核函數是式(3).

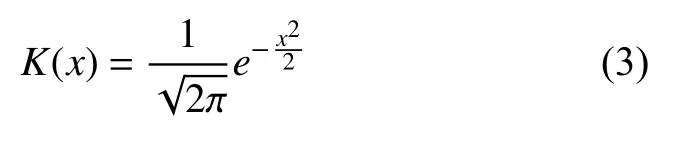
1.2 理論分析

基于上述對圖2的分析，可以得到如下的結論：

也真是奇怪，有些事情，苦思冥想往往找不到解決的途徑，一旦放松下來，甚至把它撂在了一邊不去管它，頭腦中或許會一瞬間跳出一個天才的解決方案。此時，在與“詩的妾”打情罵俏的短信中，一個想法突然在高潮頭腦中清晰起來。高潮有些興奮，站起身來，拍拍屁股，真的沖著湖面，大叫了幾聲。湖對面的那流浪青年停下練唱，用中氣十足的嗓音對高潮喊道，不服氣啊哥兒們，有本事你也來段海豚音？

結論：線段L的中心點沿著曲線移動，局部能量值是不斷變化的，當線段的中心點與邊緣點重合時，局部能量達到最大值.

證明. 在圖2中，局部能量函數在邊緣點x=0處達到最大值.

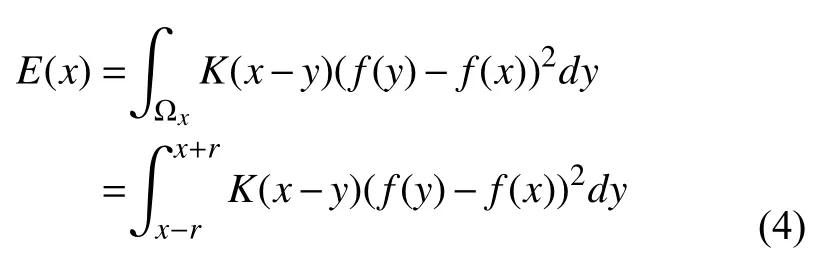
假設x-y=τ,y=x-τ,dy=-dτ得到

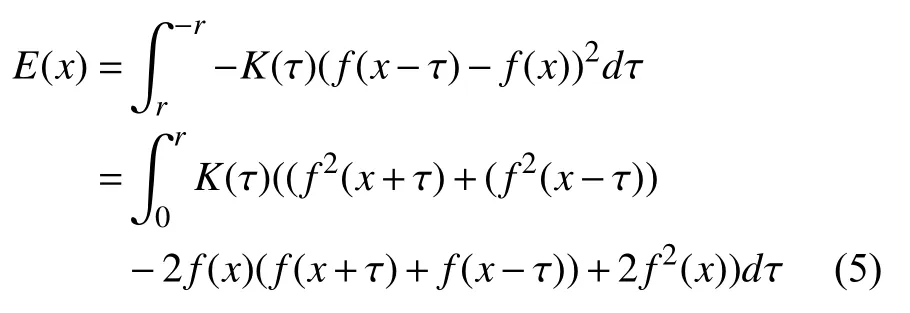
對式(5)求導數得：

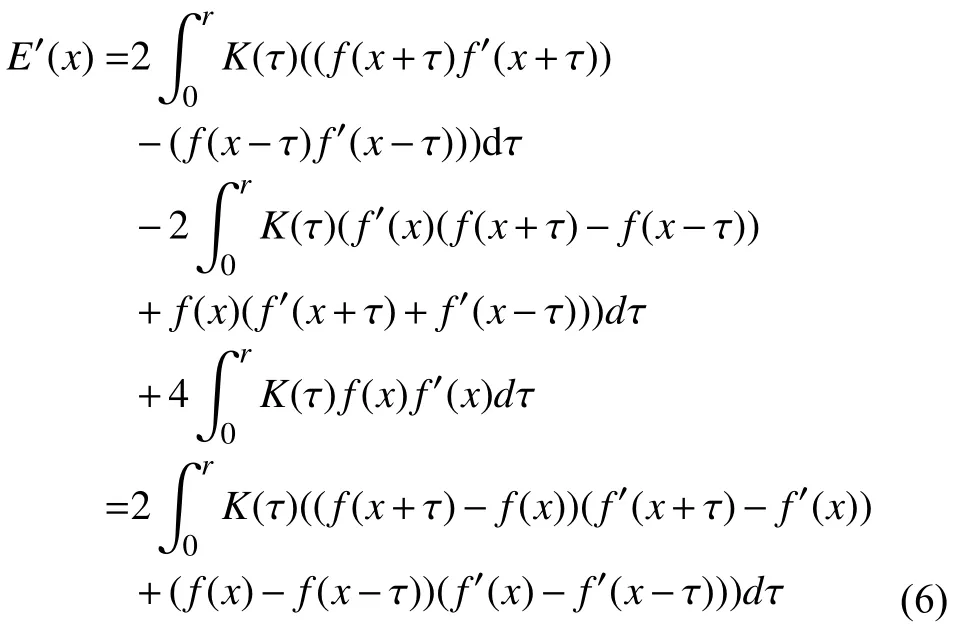
當x=0時

如圖1所示，函數f(x)是奇函數，f(x)的導數是偶函數. f(x+τ)-f(x-τ)是大于零的常數. 當x＜0，導函數f′(x)是單調遞增的，當x＞0時單調遞減，滿足對稱性.

因為，f(x+τ)-f(x)和f(x)-f(x-τ)大于零，所以

(1)當x-τ＜0,x＞0，即x∈(0,τ)，f′(x+τ)-f′(x)＜0，f′(x)-f′(x-τ)＜0.

(2)當x-τ＞0，即x∈(τ,∞)，f′(x+τ)-f′(x)＜0，f′(x)-f′(x-τ)＜0.

綜上所述，只要滿足x＞0，E′(x)的值是恒小于零的，因此，當x＞0時局部能量函數E(x)是一個單調遞減函數.

同樣的，根據f′(x)的對稱性，當x＜0時，局部能量函數E(x)是單調遞增函數. 因此，局部能量函數在邊緣點x=0取得大值. 在實驗中，我們通過調整閾值得到邊緣點.

例如，如圖3(a)所示，x=0處的跳變點為邊緣點.如圖3(b)所示，局部能量最大值點也在x=0處.

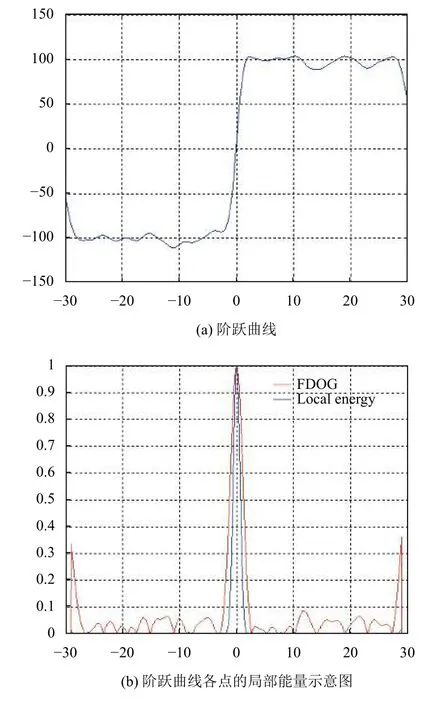
圖3 階躍曲線及其各點對應的局部能量示意圖

本文提出了一種基于局部能量的邊緣檢測方法，當中心點位于對稱區域中的光滑區域時，局部能量值比較小，當位于邊緣點時，局部能量達到最大值. 因此，可以通過局部能量的最大值來快速準確的確定邊緣點位置.

本文方法的算法步驟如下：

步驟1. 輸入圖像;步驟2. 使用高斯核函數對圖像進行預處理;步驟3. 邊緣檢測響應采用式(2)的局部能量函數;步驟4. 選擇適當的閾值進行處理;步驟5. 輸出邊緣映射圖.

2 數值實驗

在本節中，通過一系列的實驗驗證了該方法的有效性. 實驗中使用的圖像包括正常圖像、合成圖像、醫學圖像以及Berkeley分割數據集(BSDS)中圖像. 本節分兩部分進行實驗：1) 與常用邊緣檢測方法的對比;2) 通過Baddeley誤差度量(BEM)[20]方法進行的數值比較.

2.1 與常用邊緣檢測方法對比實驗

本文方法與常用邊緣檢測方法對合成圖像和醫學圖像的邊緣檢測結果對比如圖4、圖5、圖6所示.

圖4 本文方法與常用邊緣檢測方法對合成圖像的邊緣檢測結果示意圖(括號中數值為從上到下閾值). (a)原圖; (b) 本文方法(0.4，0.15，0.27); (c) Canny (0.8，0.35，0.45); (d) Sobel(30，5，9); (e) Prewitt (30，5，8); (f) LoG (3，0.5，0.7)

其中，圖4和圖5的第(a)列是原圖，第(b)-(f)列分別是采用本文方法、Canny方法、Sobel方法、Prewitt方法和LoG方法的邊緣檢測結果. 從圖片效果上看，本文方法的檢測結果要優于其它方法.

圖6的第二行圖像是在第一行原圖的基礎上加了標準差為0.05的高斯噪聲圖像，第四行圖像是在第三行原圖的基礎上加了標準差為0.1的高斯噪聲圖像. 實驗結果表明，本文方法能得到更好的檢測結果.

圖7為本文方法與其他文獻所提方法的比較，從實驗結果來看，本文方法能得到較好的邊緣檢測結果.

圖5 本文方法與常用邊緣檢測方法對醫學圖像的邊緣檢測結果示意圖(括號中數值為從上到下閾值). (a)原圖; (b)本文方法(0.25，0.26); (c)Canny (0.3，0.45); (d) Sobel (17，5); (e)Prewitt(12，5); (f) LoG (0.2，0.4)

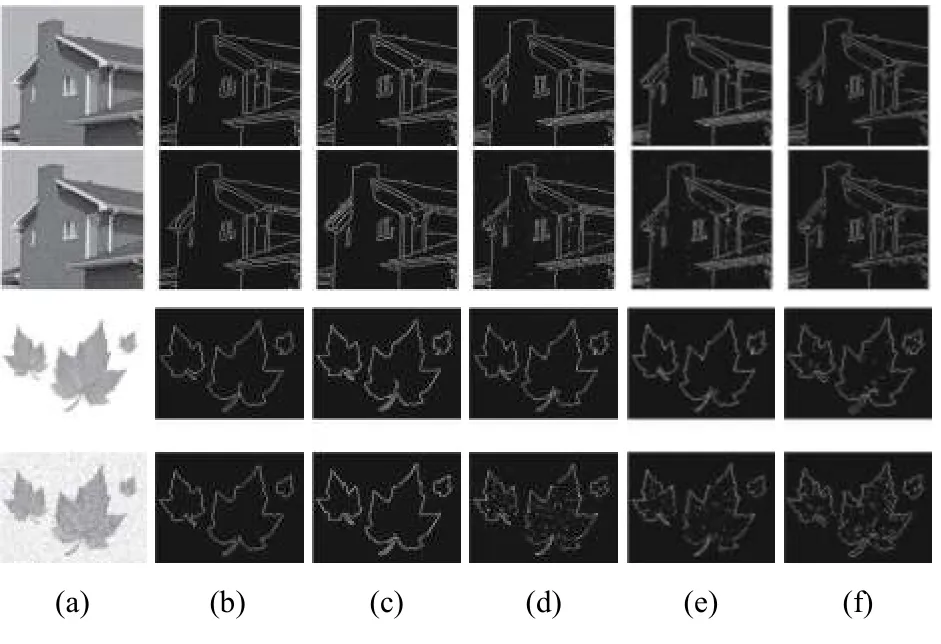
圖6 本文方法與常用邊緣檢測方法對原圖與添加了高斯噪聲圖像的邊緣檢測結果示意圖(括號中數值為從上到下閾值). (a)原圖; (b)本文方法(0.19，0.19，0.2，0.3); (c) Canny(0.19，0.17，0.3，0.5); (d) Sobel (15，19，15，30); (e) Prewitt(15，18，15，30); (f) LoG (1.5，1.5，1.2，1.8)

圖7 本文方法與其他文獻檢測方法的對比

2.2 BEM對比試驗

在本節中，通過對不同條件下的相同圖像進行實驗來比較本文方法和其他方法. 為了進行定量比較，本文使用 Baddeley誤差度量(BEM)[20]方法進行實驗驗證. 兩個二進制圖像的不同之處是由BEM計算的. 這些實驗是在不同類型的Berkeley分割數據集(BSDS)[21，22]圖像上進行的. 在本節實驗中使用了很多不同場景下的圖像.

因為邊緣映射圖像通常是以二進制的形式顯示，因此，它可以使用BEM方法進行比較研究. I1和I2是兩個二進制圖像，有相同的維度N×M，p={1,···,N}×{1,···,M}是像素位置集合. I1是BSDS中給出的真實的邊緣圖像，I2是邊緣檢測方法獲得的邊緣圖像. k-BEM(0＜k＜∞)的定義如下：

其中，ω是一個用于權重的凹遞增函數，d(p,Ii)表示點p到最接近的邊緣點的Ii距離. 實驗中所要用到的距離函數，選擇使用歐幾里得距離公式. 根據文獻[23，24]，在所有的BEM對比實驗中，選擇統一使用k=2和ω(x)=min(c,x)，其中

BEM方法是用來比較兩幅二進制圖像之間的差異性的. 所以，通過BEM方法得到的實驗結果越小，說明兩幅圖像間的差異性越小，也就意味著邊緣檢測得到的結果越接近BSDS數據庫中給出的真實邊緣圖像.

將本文方法和其他方法應用到Berkeley分割數據集(BSDS)的10個測試圖像中，把不同方法得到的二進制圖像與BSDS中給出的真實邊緣圖像使用BEM方法計算不同之處，并將本文方法與其他方法得到的實驗結果進行比較. 實驗中用到的圖像分為兩類：原圖像和添加高斯噪聲圖像.

使用邊緣檢測方法來處理圖像時，選擇不同的閾值進行實驗，通過對閾值大小的不斷調整，選擇一個最接近實際邊緣的二進制圖像進行比較. 這樣得到的實驗結果是比較合理的.

表1 本文方法與其他方法對原圖使用BEM方法得到的實驗結果

表1為采用本文方法與其他算法針對原圖進行邊緣檢測的BEM值對照表. 表1中第一列為BSDS數據庫中的圖像編號，第2-9列分別為Canny0.75、Canny1.5、Prewitt、Sobel、LoG、Ant算法[23]、GED-T[24]、GEDEA[25]和本文方法的BEM值(其中，Canny0.75表示Canny方法采用閾值為0.75的情形). 表1中的最后一行的sum項為各種方法處理數據庫圖例的各項BEM值的總和. 從表1可以看出，本文方法的檢測結果中至少有6幅圖像的結果是優于其他幾種方法方法. 例如，BSDS數據庫中圖像編號為69015的圖像，本文方法的BEM值比其他幾種方法的BEM值都要小，也就是說，本文方法與其他幾種邊緣檢測方法相比，邊緣檢測得到的結果更接近BSDS數據庫中給出的真實邊緣圖像. 但也有幾幅圖像的實驗結果并不都是最小的，如圖像編號為54082的圖像，本文方法檢測到的結果并不是最好的，但與其他方法相比也是可以接受的，而且表1中所有圖例的BEM總和也是最小的.

表2為采用本文方法與其他算法針對添加噪聲的圖像進行邊緣檢測的BEM值對照表. 噪聲圖像是在原圖像的基礎上，添加了標準差為0.1的高斯噪聲得到的. 表2中的數據顯示，本文方法針對含噪聲圖像的邊緣檢測結果中至少有6幅圖像的結果是比其他幾種方法得到的結果都要小，說明針對噪聲圖像，本文方法得到的檢測結果也是比較接近BSDS數據庫中給出的真實邊緣圖像. 因此，本文方法對含有少量噪聲的圖像的邊緣檢測也是有效的.

表2 本文方法與其他方法在添加噪聲的圖像中使用BEM方法得到的實驗結果

表1和表2給出的數據中，本文方法無論是對原圖還是對添加了高斯噪聲后的圖像的檢測結果都有超過半數是比其他方法檢測到的數值要小. 根據BEM方法的理論知，數值越小，檢測到的結果越接近數據庫中給出的邊緣圖，說明檢測結果的準確性越高. 因此，本文方法的優勢在于檢測結果相對于其他幾種方法來說是比較好的.

3 結論

本文提出了一種新的基于局部能量的圖像邊緣檢測方法. 局部能量最大的點對應于邊緣點. 通過局部能量，可以有效地找到邊緣點. 通過大量的實驗驗證，本文方法無論是從視覺效果上還是BEM定量結果上，與其他方法相比，都能得到比較好的檢測結果.