某型無人機火箭助推發射系統設計及分析

安佳寧

(中國人民解放軍92419部隊，遼寧興城 125106)

火箭助推發射型無人機,在助推火箭的作用下,可在很短的時間內獲得起飛速度和一定的飛行高度,然后火箭自行脫落,無人機在發動機的作用下繼續飛行。這種起飛方式機動性好,不受機場條件的限制,而且還可在地面或艦艇上進行發射起飛,擴大了無人機的使用范圍,因而是一種常用的無人機發射方式。根據火箭助推器的使用數量可分為單發火箭助推和多發火箭助推,選擇何種方式由無人機結構形式和氣動布局決定[1],例如，美國“石雞”無人機由于采用腹部進氣,因此采用翼根布置2枚助推火箭的發射方式[2]。根據火箭助推器推力線與機身縱軸的相對位置,可分為夾角式和共軸式2種。夾角式助推方式推力座設置比較簡單,但推力線控制與調整比較復雜,火箭脫落時容易與發動機發生干擾。共軸式助推方式,加速快,但推力座設置復雜,而且與無人機發動機協調困難[3]。某型無人機采用背部S彎進氣道后置渦噴發動機布局方式,綜合考慮各種因素,采用下托式單枚火箭助推夾角式發射方式,在無人機總體方案對發射系統技術要求一定的情況下,發射系統的設計主要集中在2個方面:1)發射架系統的設計;2)發射參數的選擇。高速無人機不同于低速無人機橫向轉動慣量小,發射過程中受到擾動容易出現大角度滾轉,特別是火箭助推器將無人機重心大幅度后移,造成了無人機靜穩定度降低,甚至變為靜不穩定,給發射控制帶來難度[4-5]。筆者在對高速無人機發射架設計的基礎上,對發射過程進行了詳細分析,建立了發射過程仿真模型。在建模過程中將無人機和火箭作為組合體進行分析,對氣動力矩系數進行了修正,考慮了火箭助推器的氣動力和組合體重心變化影響，編寫了仿真程序并對發射過程相關參數的選取進行了分析,給出了火箭推力線下偏的合適角度來抵消渦噴發動機帶來的低頭力矩。實際飛行檢驗了設計方案和參數選取的合理性。

1 發射架系統設計

發射架系統設計主要包括發射架設計、助推器連接方式和脫落方式選擇。

1.1 發射架設計

目前，零長發射架主要有2種:倒伏式發射架和短軌式發射架。倒伏式具有發射架重量輕的優點;短軌式具有發射初段抗干擾能力強的優點，但是整個發射架重量較大,為了具有較強的機動性,選擇倒伏式發射架,如圖1所示。該發射架在確定發射位置后可以調平并用錨釬固定在地面上,發射架的發射角可以借助調整螺母在10°～20°之間進行調整。發射架設有前倒機構,無人機機身前段設備艙兩側的支撐點在發射時支承在前端支撐的叉形件上,發射時前端支撐隨著無人機的運動向前倒下,以避開機體后面的進氣道和平尾等部件。發射架還設有一個后端支撐,在無人機機身后段發動機艙下面中間位置的支撐點就支承在發射架的后端支撐上。發射架上設有閉鎖機構以保證無人機在火箭助推器啟動前不會因發動機的推力發生運動,只有當火箭助推器點火后達到一定推力時切斷支架上的剪斷螺栓,無人機才能被發射起飛[6]。

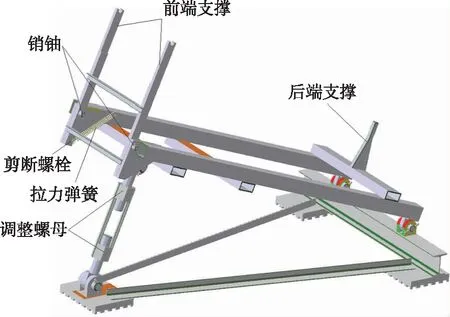
圖1 發射架結構

1.2 連接方式選擇

在無人機后機身下部安裝有頂錐,頂錐軸線與機身軸線夾角為推力線夾角,助推器頂桿頭部為錐窩,錐窩軸線與助推器軸線共軸。助推器安裝如圖2所示,頂桿錐窩與機身頂錐配合,約束助推器頭部軸向、周向自由度,同時助推器尾部支撐在發射架后支架上,后支架與助推器托環配合,約束助推器尾部軸向、周向自由度。發射前助推器借助頂錐、發射架后支撐組件共同作用,保證助推器與無人機連接。助推器點火工作時,在推力作用下，頂錐、頂桿錐窩錐面自適應配合,保證推力線相對機身軸線要求。當剪切銷剪斷后,無人機在助推器推力作用下向上運動,發射架后支撐組件與助推器約束解除。當助推器工作完畢,在助推器重力和氣動阻力作用下，助推器與無人機分離。

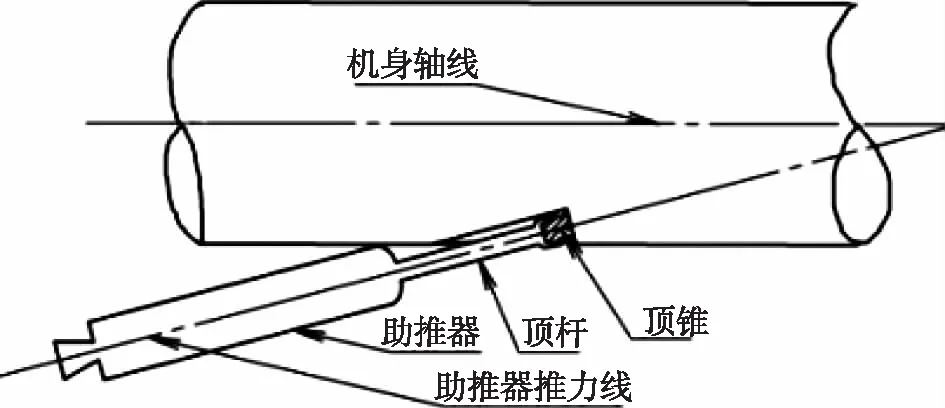
圖2 助推器安裝

2 發射過程建模

火箭助推階段動力學模型可以分為3個階段討論:助推點火——飛機未脫離發射架階段、脫離發射架——助推結束、助推器脫落階段。由于本無人機采用的是零長發射,沒有滑軌,因而，無人機在發射階段,其受力過程可以分為2個階段:火箭助推段和火箭脫離后的加速爬升段,其中，火箭脫離后的加速爬升段受力與空中段相同。火箭脫落過程雖然短暫,但是其對無人機姿態有較大影響。由于發射過程時間較短,因此認為在整個發射過程中無人機質量不變(燃油不消耗),轉動慣量不變,無人機和火箭組合體的質心和轉動慣量的變化由助推火箭重量和轉動慣量的變化引起。根據固體火箭燃燒方式(由中心向外側燃燒)可以認為助推火箭在整個發射過程中質心位置不變,質量逐漸減小。在此基礎上可以建立無人機發射過程中的六自由度動力學和運動學方程[7]。

在無人機發射過程中,受到的外力包含有:重力、空氣動力、發動機推力、助推火箭推力、發動機進排氣產生的力以及力矩等;氣動力靜導數由風洞試驗獲取,加工的風洞試驗模型進氣道入口和尾噴管進行了修型處理,因此獲取的氣動數據必須進行發動機進排氣影響修正(進排氣對升力特性影響較小,對阻力特性和俯仰力矩特性影響較大,最大升阻比降低了2左右,并產生顯著的抬頭力矩)。因此，無人機受力情況綜合表示如下所示。

F=Faerodynamic+Fturbo-jet+Frocket+g

(1)

M=Maerodynamic+Mturbo-jet+Mrocket

(2)

2.1 氣動力模型

氣動升力、阻力、側力通常是在風軸系進行表示和定義的,表示為

(3)

氣動俯仰力矩、滾轉力矩及偏航力矩通常是在體軸系進行表示和定義的,表示為

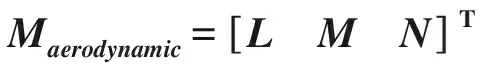
(4)

無人機在發射階段,空氣動力存在很強的非線性,因此不能用簡單的線化方程來描述,其表達式如下所示。

升力系數

(5)

阻力系數

CD=CD(α、δe、Ma)

(6)

俯仰力矩系數

(7)

側力系數

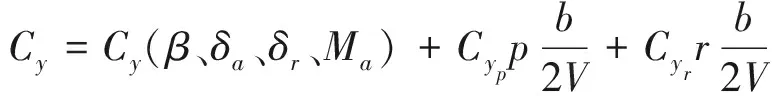
(8)

滾轉力矩系數

(9)

偏航力矩系數

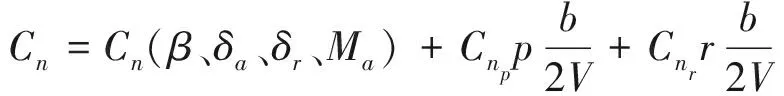
(10)

由于CFD仿真和風洞試驗力矩系數均以無人機重心為參考點,而發射過程中由于助推火箭的影響,力矩系數參考點的位置發生偏移，改變為以組合體重心作為參考點。重心偏移的定義為:ΔXG=XG-Xref,當重心后移時ΔXG>0。ΔYG=YG-Yref,當重心向右機翼方向移動時ΔYG>0。 ΔZG=ZG-Zref,當重心向下移動時ΔZG>0。發射過程中隨著火箭藥柱的燃燒ΔXG、ΔYG、ΔZG在不斷變化。

動態力和力矩系數修正公式如下:

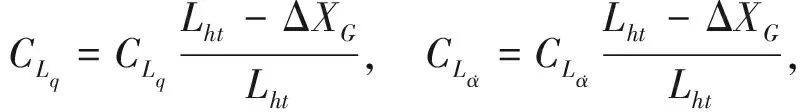
靜態空氣動力需要修正的是力矩系數,修正方法如下。

俯仰力矩系數修正

(11)

滾轉力矩修正

ΔCl=(CL·ΔYG+Cy·ΔZG)/Lspan

(12)

偏航力矩修正

ΔCn=(CD·ΔYG+Cy·ΔXG)/Lspan

(13)

由于助推火箭采用了短粗構型,其截面直徑達到無人機機體直徑的一半,而且距火箭和無人機組合體質心較遠,可能產生一定量的俯仰力矩,因此在仿真過程中未忽略助推火箭的升阻力,其升阻力系數采用如下模型:火箭可視為等直徑的圓柱體,圓柱體氣動力系數如圖3所示(圓柱體參考面積定義為橫截面直徑D×長度L)。

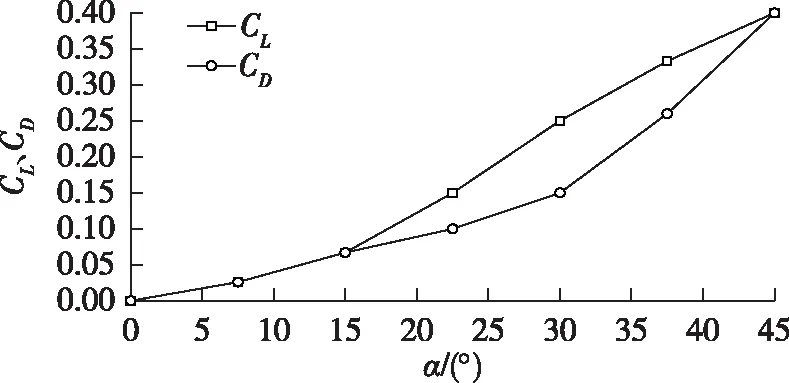
圖3 圓柱體氣動系數經驗曲線

火箭迎角定義為:αrkt=αUAV+η,其中η為火箭安裝角。相對于無人機與火箭組合體重心,火箭氣動力產生的俯仰力矩系數修正為

碳關稅的本質是一種出口稅，其征收體現在出口商品的價格變化中，本文以中國出口至美國商品征收碳關稅為例，則出口方程可由式(6)

(14)

其中lrkt→cg為火箭重心到組合體重心的距離。

2.2 發動機推力數學模型

發動機推力在機體坐標系中的表達式如式(15)所示,對本型無人機來說,發動機安裝角為零,即發動機推力軸線平行機身軸線,因此Py=0,Pz=0。

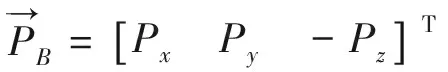
(15)

投影到氣流軸系表示為

(16)

渦噴發動機安裝在機身軸線上,通過無人機重心,但不通過無人機和火箭組合體重心,會產生低頭力矩,其表達式為:

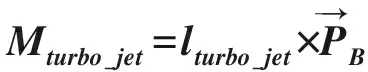
(17)

(18)

式中lturbo-jet為渦噴發動機推力作用點位置向量。

2.3 火箭作用力數學模型

火箭的推力通常在體軸系中表示

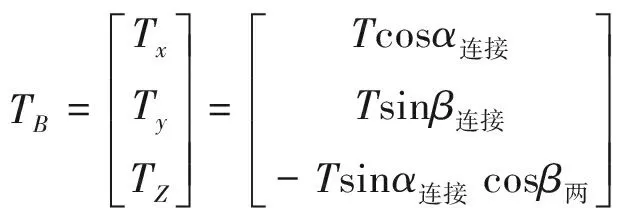
(19)

其中:α連接為火箭軸線與機體OXZ平面的夾角;β連接為火箭軸線與機體OXY平面的夾角,正β兩使推力產生正側力分量。

在氣流軸系中表示為

TW=LWBTB

(20)

在助推火箭推力線不通過重心情況下,火箭推力對無人機的力矩作用為

Mrkt=lrkt×TB;

(21)

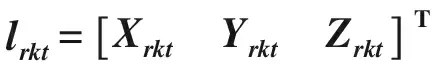
(22)

式中，lrkt為火箭推力作用點位置向量。

火箭脫落后無人機受力為正常飛行受力。

3 發射過程控制模型

無人機發射過程中控制的首要目標是保證無人機姿態的穩定,因此整個發射過程不進行外回路控制。由于航向角控制會導致無人機出現較大的滾轉角,因此也不進行航向角控制。整個發射過程只進行俯仰角控制和滾轉角控制。由于發射段氣動力參數等與正常飛行時不同,因此在發射段控制參數與正常飛行段控制參數的選取上略有不同。控制率數學模型如公式(23)和公式(24)所示。

UδE=Kqq+Kθ(θC-θ)

(23)

UδA=Kpp+Kφ(φC-φ)

(24)

4 火箭安裝偏差范圍

在火箭助推段無人機剛脫離發射架時飛行速度小,高度低,舵面無法充分發揮其氣動效率,因而在此階段,重點在于選擇合適的發射參數,在綜合各種因素后選擇具體發射參數如下:火箭安裝角15°,發射架傾角17°。由于采用吊掛方式對推力線進行校準,存在操作誤差,為保證無人機正常起飛必須對火箭安裝角偏差范圍進行仿真計算。利用Matlab編制了仿真程序,對整個發射過程進行了仿真,仿真時間10 s,在此過程中不對無人機發送任何指令。火箭助推器常溫基準工作時間為2.5 s。

4.1 火箭安裝角縱向偏差范圍

在發射參數確定后,發射過程穩定性主要受到火箭安裝偏差的影響,當火箭推力線未通過無人機和火箭組合體重心時會帶來側偏力矩,由于發射過程中無人機舵面效率低,如果側偏力矩過大,舵面無法糾正,將導致無人機發生翻轉,發射失敗。縱向偏差是指火箭實際推力線與過組合體重心推力線之間存在上下偏差,經過組合體重心上方或下方,因此會產生低頭力矩或抬頭力矩。渦噴發動機推力線經過機身縱軸,因此在發射階段渦噴發動機推力線在無人機和火箭組合體重心的上方,會產生低頭力矩,為了平衡這個低頭力矩,應該使火箭推力線經過組合體重心的下方,即負夾角。經過初步分析選取-0.3°、-0.4°、-0.5°、-0.6° 4個角度進行仿真分析如圖4所示。可以由俯仰角變化曲線看出,雖然推力線下偏了-0.3°,但是俯仰角依然在火箭工作段逐漸變小,直到-0.5°才穩定在15°左右。

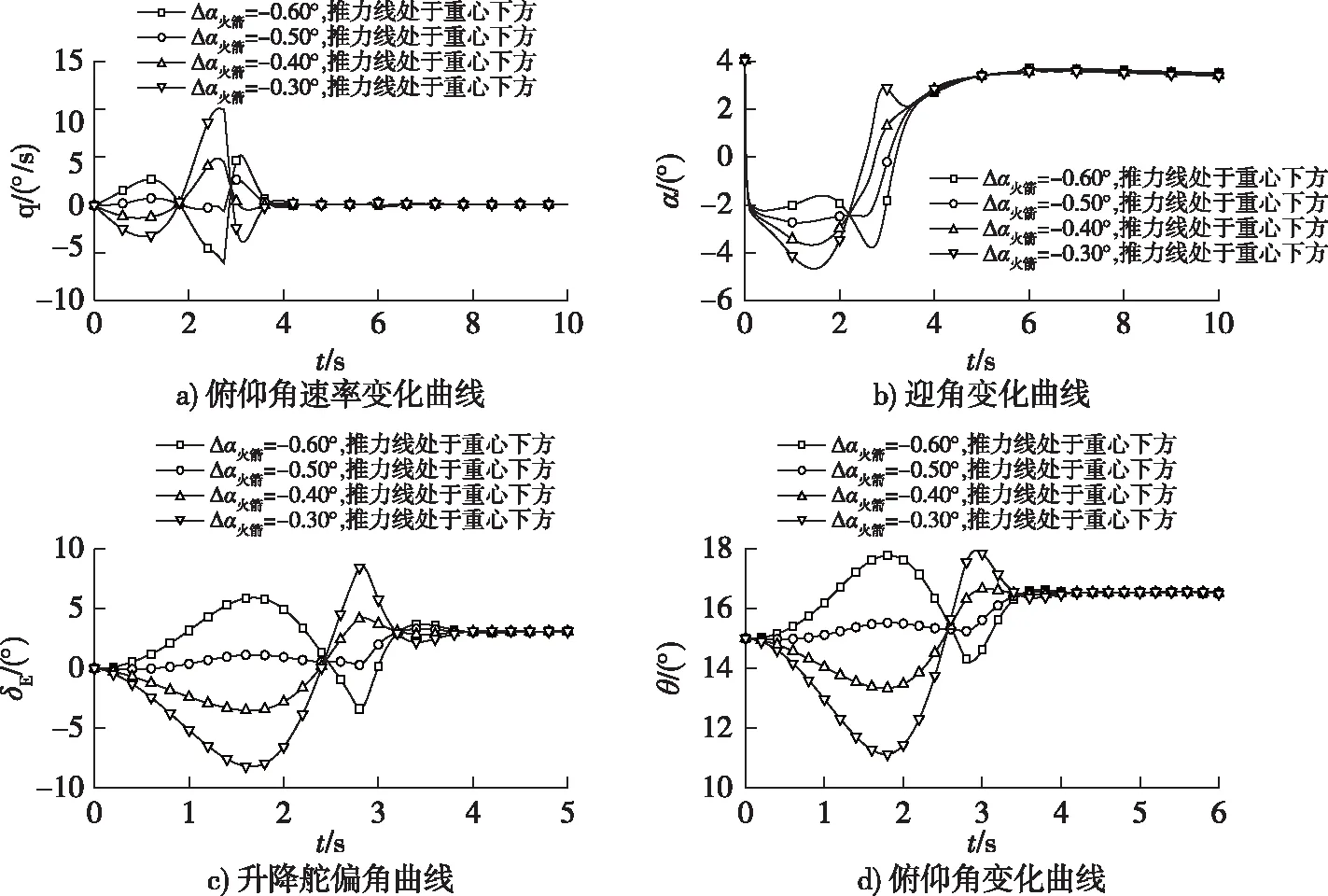
圖4 不同負夾角下無人機飛行狀態變化曲線

4.2 火箭推力線橫向偏差范圍

火箭推力線橫向偏差是指火箭實際推力線與過組合體重心推力線之間存在左右偏差,經過組合體重心左側或右側,因此會導致無人機在發射過程中產生滾轉和偏航。對于高速無人機來講，一般采用小展弦比的氣動布局,這就導致無人機的橫側向轉動慣量要比俯仰轉動慣量和偏航轉動慣量小很多倍。無人機對橫側向擾動十分敏感。從圖5仿真曲線可以看出推力線橫向偏差0.5°時,雖然最終可以將滾轉角穩定到0°左右,但是在起飛1 s后滾轉角達到了28°,副翼偏角達到了19°接近23°舵機電限位。

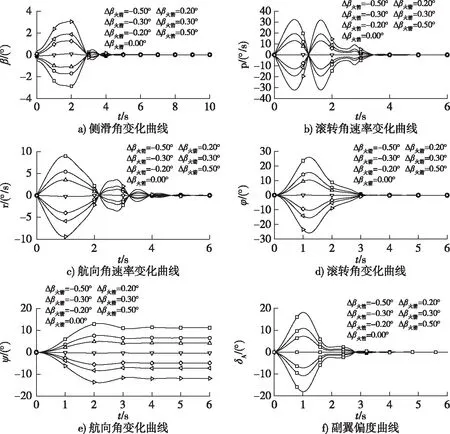
圖5 不同推力線橫向偏角影響曲線

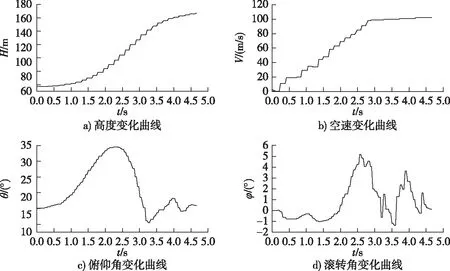
圖6 試飛無人機發射段狀態曲線

5 試驗結果分析

本文在對仿真結果進行充分分析的基礎上,結合實際工程經驗,將某型無人機的助推火箭安裝角為15°,發射角為16°。推力曲線向下偏-0.6°。實際發射曲線如圖6所示。火箭實際工作時間約為2.8 s,火箭工作結束后飛行速度達到98 m/s,基本滿足設計指標,由俯仰角變化曲線可以看出,在火箭工作前2 s由于空速較低舵面效率低,無人機和火箭的組合體受到火箭推力線偏差引起的俯仰力矩的作用,俯仰角不斷增大,最大達到了33°,2 s以后舵面效率逐漸上升,俯仰角逐漸下降最終穩定在15°左右,整個發射段滾轉角變化較小,最大值約5°,基本滿足發射指標要求。通過實際發射試驗驗證了發射系統的基本性能,通過與仿真數據對比可以看出,推力線下偏-0.5°俯仰角在發射初段增加過快,因此在后續發射過程中將推力線調整為下偏-0.4°。

6 結束語

本文設計了某型無人機火箭助推發射系統,該系統采用零長倒伏式發射架,該發射系統滿足發射需求,質量較小,便于機動發射,通過對發射過程進行受力分析,在建立發射過程數學模型的基礎上,編寫了仿真程序,研究了安全發射條件。結合工程實踐對某型無人機發射參數進行了選取,實際飛行數據表明,設計參數合理,滿足無人機火箭助推發射需求。