基于MDP的血小板庫存最優訂貨策略和使用策略研究

李 猜， 耿 娜， 王春鳴

(1.上海交通大學 工業工程與管理系，上海 200240； 2.上海交通大學 中美物流研究院，上海 200030; 3.上海交通大學 醫學院附屬仁濟醫院，上海 200127)

0 引言

血液是一種特殊的稀缺資源，主要有以下五個特點：(1)血液產品屬于易逝品，有一定的保質期，一旦過了保質期就不能再用于輸血；(2)供給相當不規則，因為血液產品的供給完全依賴于獻血者捐獻；(3)需求隨機且分類，一般可分為普通需求和緊急需求，普通需求可積壓(部分手術可擇期)，緊急需求不可積壓；(4)普通需求的積壓成本相對較低，緊急需求的缺貨成本相對較高，需要通過高成本的緊急采血或者臨時調配進行處理，否則患者可能有生命危險；(5)過期不容易被接受，因為不僅要避免稀缺資源的浪費，還要考慮獻血者的心情，尊重獻血者的貢獻。因此，血液產品的庫存管理一直是易逝品庫存研究的熱點和難點[1,2]。血液產品中血小板保質期較短，為5到7天，從采集到檢測一般需要2天，供給醫院可使用的有效時間只有2～3天。輸血時血小板的新鮮度對患者的健康會產生不同影響，Joyce等[3]和Keuren等[4]發現輸注1～3天的新鮮血小板比較好，4～5天的血小板被認為隨著血小板的壽命變化，可能產生被認為是有害的物質。根據Eder等[5]，85%的敗血癥輸血反應發生在輸血年齡為第四天或者第五天的時候，時間越長，風險越大。Haijema[6]和Kort等[7]認為輸注更新鮮的血液更有效。美國近期發布的輸血服務指南草案已經提出盡量減少輸注第四天或者第五天的血小板的比例，但是并非強制執行[2]。血小板的庫存管理除了考慮傳統的平衡浪費和短缺成本進行訂貨決策外，還需要考慮血小板輸注時的新鮮度對患者健康的影響進行使用策略(Issuing policy)決策。訂貨策略確定每次補充的新鮮血小板的數量，使用策略確定輸注血小板時不同新鮮度血小板的使用順序。因此，本文主要針對血小板庫存管理中的兩個問題，即訂貨與使用策略，進行研究。

血小板的庫存管理在理論與實踐中都是非常具有挑戰性的，實踐中常用的訂貨策略多為基于經驗的閾值策略，即每次都補貨到一個經驗庫存水平；血小板的使用策略上，由于血液資源的稀缺性，醫院為了避免浪費，一般會選擇先用陳舊血小板(First In First Out, FIFO)的使用策略。對于血小板的訂貨和使用策略，訂貨過多會造成不必要的浪費，訂貨過少會產生短缺。使用FIFO策略會減少短缺和浪費，但會降低平均輸血新鮮度(即增加平均輸血年齡)；新鮮血小板先用(Last In First Out, LIFO)的策略可以提高平均輸血新鮮度(即減少平均輸血年齡)，但會增加短缺和浪費。訂貨策略和使用策略之間會產生相互影響，訂貨策略不同會影響庫存中新鮮血小板量從而影響使用策略；使用策略不同會影響庫存中不同剩余壽命(Shelf life)血小板的分布狀態，進一步影響訂貨策略。為了優化血小板的庫存管理，本文通過構建有限時域的馬爾科夫決策(MDP)模型，考慮需求隨機到達，以效用最大化為目標，探討血小板的最優訂貨和使用策略，以盡可能減少短缺和浪費并提高平均輸血新鮮度；通過對最優策略數值解的觀察，提出近似的啟發式策略，并通過數值實驗驗證其性能。

1 文獻綜述

廣義上來說，本文屬于易逝品庫存的范疇，需要進行分年齡庫存管理。早期易逝品庫存文獻多關注以最小化短缺和浪費為目標的訂貨策略。如Nahmias[8]利用動態規劃對提前期為0且壽命為m的易逝品的最優訂貨問題進行了詳細的分析，但m較大時會引起“維度詛咒”(Curse of Dimension)，導致模型難以求解。后來的學者開始考慮用啟發式算法或者仿真方法來研究問題，如Nahmias[9]考慮使用啟發式方法對易逝品訂貨的動態規劃模型進行近似求解。傳統的易逝品庫存問題一般假設物品效用與壽命無關，即只要物品沒有過期，其效用就是固定的[10]。易逝品的使用策略一般會根據特定研究對象來確定，比如超市中的易逝品使用策略一般取決于顧客行為特征，對于一些保質期較短的產品顧客一般傾向于拿最新鮮的，而對保質期稍長的產品則可能會隨機選取。

血液庫存問題的研究是從20世紀60年代開始的，在20世紀70年代末和80年代達到頂峰，然后顯著下降[11]。早期的研究多數針對全血，近期的文獻則更多關注紅細胞，針對血小板的庫存管理文獻相對較少。就研究方法而言，最常見的研究方法是動態規劃和計算機仿真技術，還有少量文獻采用排隊論方法。Haijema等[12]結合隨機動態規劃和仿真提出了一種新的多步驟的啟發式方法來解決血小板的訂貨問題，尋找近似最優的訂貨策略，結果發現簡單的閾值訂貨策略幾乎保持最優。Asllani等[13]將一個基于仿真的決策支持系統用于單采血小板的庫存管理，減少了單采血小板的浪費。Civelek等[14]假設血小板補貨的提前期為0，提出了一種針對血小板庫存的雙重補貨策略。雙重補貨主要是指每天早上一個固定訂貨量的訂單，然后當天其他時間根據需求選擇是否需要增加快速補貨訂單。作者發現在正常訂單之間增加快速補貨訂單可能是管理血小板庫存的有價值的實踐。普通補貨策略主要關注短缺和浪費之間的平衡，雙重補貨則側重于快速補貨的成本和便利性。

絕大多數研究使用策略的文獻還停留在一些簡單的啟發式策略比較的層面上。使用策略不僅會影響輸血時血液新鮮度，還會影響剩余庫存的年齡分布，進一步影響過期和短缺率。Keilson[15]比較了固定壽命易逝品庫存系統在泊松供給和泊松需求下的FIFO和LIFO使用策略的性能，發現FIFO策略最小化了短缺和浪費但最大化了平均使用年齡，LIFO策略最小化了平均使用年齡但最大化了短缺和浪費。Atkinson等[16]針對紅細胞的使用提出了一種結合FIFO和LIFO的閾值策略，通過仿真求出該策略的短缺率和平均使用年齡，發現該閾值策略比FIFO策略的性能要好。

通過建模優化使用策略的文獻較少，Pierskalla[17]通過建立數學模型研究了易逝品庫存的最優使用策略，但是該模型中的庫存不會過期，只會惡化。Li等[18]在未過期庫存收益相同的假設下證明了易逝品庫存的最優使用策略是FIFO策略。

目前考慮輸血時血液新鮮度進行庫存優化的文獻較少[6,19,20]。Haijema[6]研究了失銷情況下易逝品的訂貨、使用和臨期處理問題。該文獻中使用策略僅考慮了FIFO和LIFO兩種情況，訂貨策略和臨期處理決策通過MDP模型來進行研究，目標是最小化短缺、浪費以及臨期懲罰成本。模型假設提前期大于0小于1，將訂貨決策和臨期處理決策分到兩個時間段以避免高維度的決策空間，發現最優的臨期處理決策對庫存管理的改進可能有實用價值。Tetteh[19]認為輸血的收益跟血小板輸注的新鮮度有關，在供給和需求確定的情況下通過仿真來比較FIFO、LIFO以及FIFO和LIFO混合策略的浪費、短缺以及平均使用年齡。Slofstra[20]研究了實際供給和實際需求下紅細胞的使用策略，構建了一個有限時域的MDP模型，以短缺、浪費以及年齡懲罰(越新鮮的血液懲罰成本越小)三種成本構建目標函數，分別在失銷和積壓的情況下進行求解。由于紅細胞的壽命較長(42天)，模型狀態空間較大，作者僅求解了單周期成本函數的短視策略。此外，該論文考慮了幾種簡單但是便于實施的使用策略，包括FIFO、LIFO、隨機策略以及幾種不同的閾值策略，并通過仿真比較以上這些使用策略的性能，找到每個成本參數集對應的表現較好的使用策略。

2 問題描述與MDP模型

2.1 問題描述與符號定義

本文針對醫院血小板庫存系統建立了有限時域的馬爾科夫決策模型，研究不確定需求下系統的最優訂貨策略和使用策略。醫院血小板的訂貨提前期為1天[12]，系統每天天初收到前一天的訂貨，更新系統狀態并發出新一天的訂單(訂貨決策)，在當天需求到達之后確定滿足需求時不同剩余壽命血小板庫存的使用量(使用決策)，并在天末丟棄過期的血小板。為了建立模型，本文做出以下假設：

假設1本文針對某一特定血型的血小板，假設血小板在醫院的有效使用時間為2天。

假設2血小板補貨的提前期為1天[12]，即第t天初下訂單，第t+1天初即可到貨。

假設3本文2.2與2.3節先后分別考慮可等待的普通需求(未滿足積壓)以及不可等待的緊急需求(未滿足失銷)，假設新的需求到達隨機，需求量服從某一已知分布。

假設4為了避免浪費與打擊獻血者的積極性，假設庫存與積壓不會同時存在。

關于血小板輸注血型問題的說明如下：根據臨床輸血技術規范[21]第十六條規定，輸注手工分離濃縮血小板的患者輸注前應進行交叉配血試驗，輸注機器單采濃縮血小板應ABO血型同型輸注。交叉配血實驗是為了在血型鑒定的基礎上進一步確保輸血安全，保證供血者與受血者之間不存在血型不合的抗原-抗體反應(人類的血型很復雜，即使是同型血之間還存在亞型的區別)。目前國內的臨床輸血規范[21]中并未涉及血小板的ABO相容性輸注，而部分發達國家的血小板輸注指南則基本包含了血小板相容性輸注規則，允許當ABO血型相合血小板供不應求時，可以輸注ABO血型不同的血小板[22]。國外大多數研究血小板庫存的文獻均未區分血型[6,7,12,14,19,23]，一般假設滿足需求時首先使用最老的同型血，同型血不足時再按照血型相容性順序選擇其他可用血型。國內臨床輸血規范[21]中雖然沒規定血小板的ABO相容性輸注，但是臨床輸血實踐證明輸注ABO血型不相同的單采血小板對于挽救急性血小板減少引起的危及生命的出血患者可以取得良好的臨床效果[22]。考慮到國內血小板ABO相容性輸注存在爭議，本文在假設1中假設模型針對某一特定血型的血小板進行研究。

由于血液中心的非盈利性，本模型忽略醫院訂購血小板的訂貨成本。另外在血液產品庫存問題中，庫存持有成本與浪費成本和短缺成本相比可以忽略不計[23]。因此模型的目標函數中僅考慮積壓成本、失銷成本、浪費成本以及不同剩余壽命血小板的輸血效用。模型的符號定義如下：

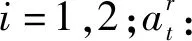
2.2 面向普通需求的血小板庫存管理MDP模型

本節面向普通需求，考慮需求在得不到滿足的情況下可積壓或延遲滿足，對血小板進行庫存控制研究。本模型的決策階段為天數t，系統狀態為(x1t,x2t)，x2t代表新鮮庫存量，x1t≥0時代表陳舊庫存量；x1t<0時代表積壓的普通需求。每個階段的決策分別為qt和yit。考慮積壓成本、浪費成本和不同剩余壽命血小板的輸血效用，可得普通需求階段效用函數：

(1)

(2)

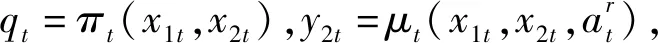
(3)

可建立普通需求下系統的目標函數為式(4)～(5)所示：

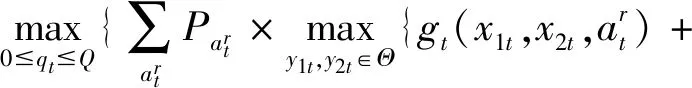
Vt+1(x1(t+1),x2(t+1))}}

(4)

VT(x1T,x2T)=0

(5)

其中第t天到第t+1天的狀態迭代關系如下：

(6)

x2(t+1)=qt

(7)

2.3 面向緊急需求的血小板庫存管理MDP模型

本節面向緊急需求，考慮需求必須盡快滿足不能積壓，在得不到滿足的情況下只能失銷，建立MDP模型，對血小板進行庫存控制研究。該模型的系統狀態和決策變量同普通需求，因為緊急需求下需求不會積壓，因此，存在x1t≥0。考慮失銷成本、浪費成本和不同剩余壽命血小板的輸血效用，可得緊急需求下的階段效用函數：

(8)

(9)

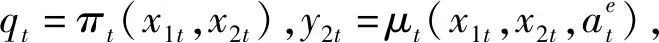
(10)

可建立緊急需求下系統的目標函數為式(11)～(12)所示：

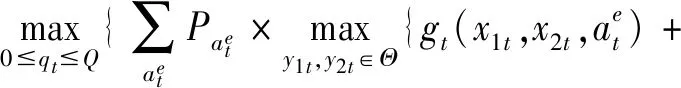
Vt+1(x1(t+1),x2(t+1))}}

(11)

VT(x1T,x2T)=0

(12)

其中第t天到第t+1天的狀態迭代關系如下：

x1(t+1)=x2t-y2t

(13)

x2(t+1)=qt

(14)

3 數值實驗

本文2.2與2.3節提出的兩個MDP模型多維度的狀態空間使得最優控制策略結構特征的證明非常困難。當狀態空間較小時，MDP模型可采用后向值迭代算法(Value Iteration)進行求解。在有限的狀態空間和有限的決策范圍前提下，值迭代算法可獲得最優控制策略的數值解[24]。但當狀態空間較大時，維度詛咒使得這兩個模型幾乎無法求解。因此，本文首先在數值實驗中觀察最優控制策略數值解的特征，然后進一步提出參數化近似啟發式控制策略，并通過遺傳算法與離散事件仿真對近似啟發式控制策略的參數進行優化，最后通過仿真實驗與敏感度分析驗證本文所提近似啟發式控制策略的性能。本文數值實驗均在Intel酷睿i5-6300HQ CPU，2.30GHz，8GB內存的環境下運行。

3.1 參數設置

考慮到患者輸血效用以及積壓、失銷和過期懲罰成本不易直接量化，本文參考了相關文獻的參數設置來進行數值實驗。目前血小板庫存文獻中考慮輸血效用的文獻相對較少，且多數文獻將血小板庫存系統考慮為單純的失銷系統，本文模型中需要用到的不同新鮮度血小板的輸血效用以及失銷、積壓和過期懲罰成本參數難以從單一的文獻中獲得參考。本文的參數設置主要參考了表1的三篇文獻，其中考慮輸血效用的兩篇文獻Tetteh[19]和Slofstra[20]均未設置Basecase，Tetteh[19]設置了一個因素水平表進行了仿真實驗, Slofstra[20]通過設置一系列不同的短缺成本和浪費成本交叉進行仿真實驗(單位輸血效用懲罰不變)。為了避免單一參數設置對實驗結果的影響，本文分別針對普通需求和緊急需求設計了四因素四水平的表格來驗證實驗結果，參數設置見表2和表3。

表1 參數設置參考文獻

表2 普通需求參數設置因素水平表

表3 緊急需求參數設置因素水平表

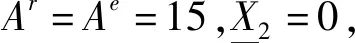
3.2 最優控制策略

3.2.1 最優訂貨策略

以cs=100,cw=80,r1=400,r2=500為例，對普通需求下的馬爾可夫決策模型通過值迭代算法進行求解，得到最優訂貨量qt隨x1t和x2t的變化規律如圖1所示，其中x2t為第t天初的新鮮庫存量，x1t≥0時為第t天初的陳舊庫存量，x1t<0時為第t天初積壓的普通需求量。觀察圖1發現普通需求下最優訂貨策略近似為帶有訂貨下限的閾值訂貨策略，其主要特征如下：

特征1隨著x1t和x2t的增加，最優訂貨量是非增的，且最多減1。

特征2最優訂貨量qt與總庫存水平(x1t+x2t)近似有一個閾值關系，多數情況下會將總庫存水平補貨至一個確定的閾值。觀察圖1可發現-12≤x1t+x2t≤2時最優訂貨策略均將總庫存水平訂貨至一個固定的閾值6，其他情況下閾值稍有變化，如x1t+x2t=3,4,5時閾值變為7。

特征3最優訂貨策略對于不同的新鮮庫存狀態x2t有不同的訂貨量下限。總庫存(x1t+x2t)一定，新鮮庫存x2t較小時需要稍大的訂貨量下限，因為這種情況下陳舊庫存相對較多，由于陳舊庫存當天結束時會由于過期而離開系統，無法應對未來需求，因此需要稍大的訂貨量下限以在第二天及時補充新鮮庫存。總庫存一定，隨著新鮮庫存x2t的增多，陳舊庫存減少，訂貨量下限逐漸降低。

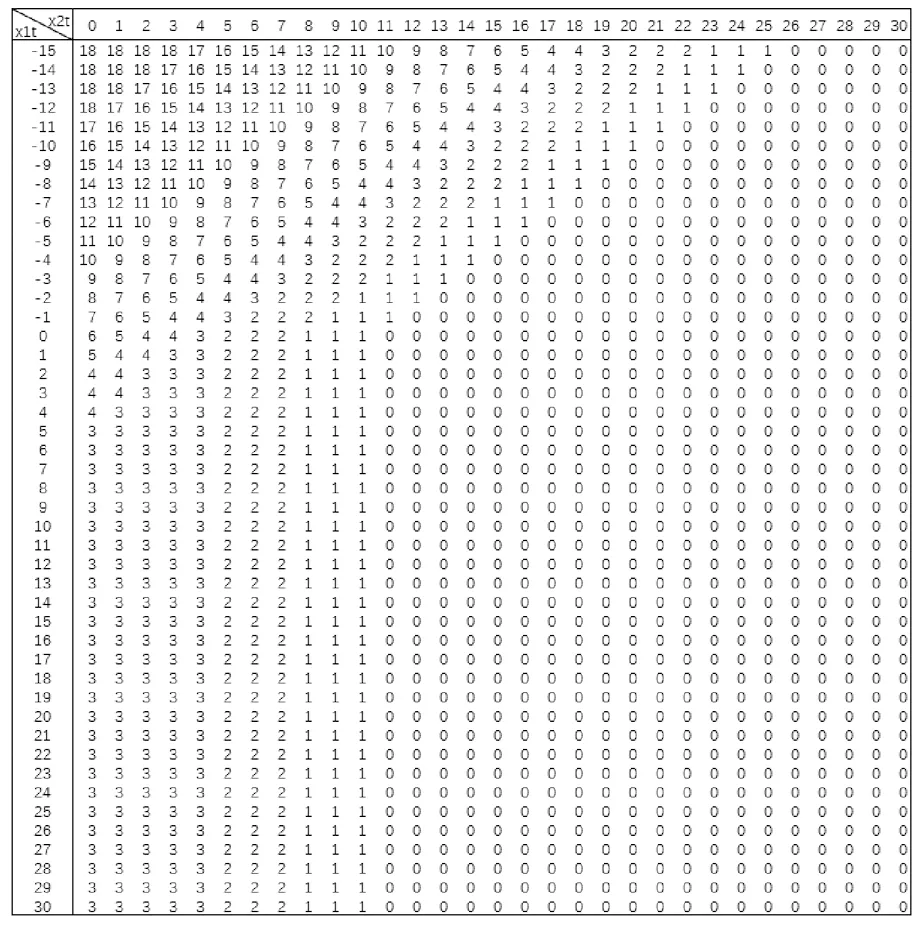
圖1 普通需求下的最優訂貨策略(以cs=100,cw=80,r1=400,r2=500為例)

分別以cs=100,cl=400,r1=400,r2=500和cs=50,cl=400,r1=450,r2=450為例，在緊急需求下對模型通過后向值迭代算法進行求解，得到最優訂貨量qt隨x1t和x2t的變化規律如圖2和圖3所示，其中x1t為第t天初的陳舊庫存量，x2t為第t天初的新鮮庫存量。觀察圖2和圖3發現緊急需求下的最優訂貨量qt主要隨著新鮮庫存狀態x2t變化，少數情況下受總庫存水平(x1t+x2t)的影響有近似的閾值結構，但是閾值相對不穩定。緊急需求下最優訂貨策略的主要特征同樣滿足上述普通需求下最優訂貨策略的三條特征，不同的是緊急需求下特征2的訂貨閾值相對不穩定，反而特征3隨新鮮庫存狀態x2t變化的訂貨下限起了主要作用。這是因為緊急需求模型中需求未滿足成本相對較高，應對未來需求不確定性的新鮮庫存x2t對系統性能的貢獻更加突出，強化了特征3。

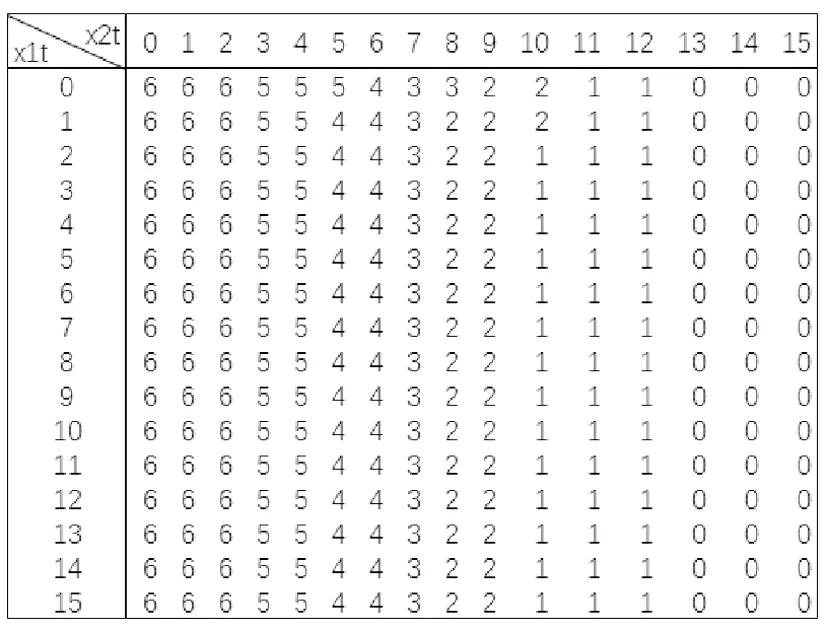
圖2 緊急需求下的最優訂貨策略(以cs=100,cl=400,r1=400,r2=500為例)

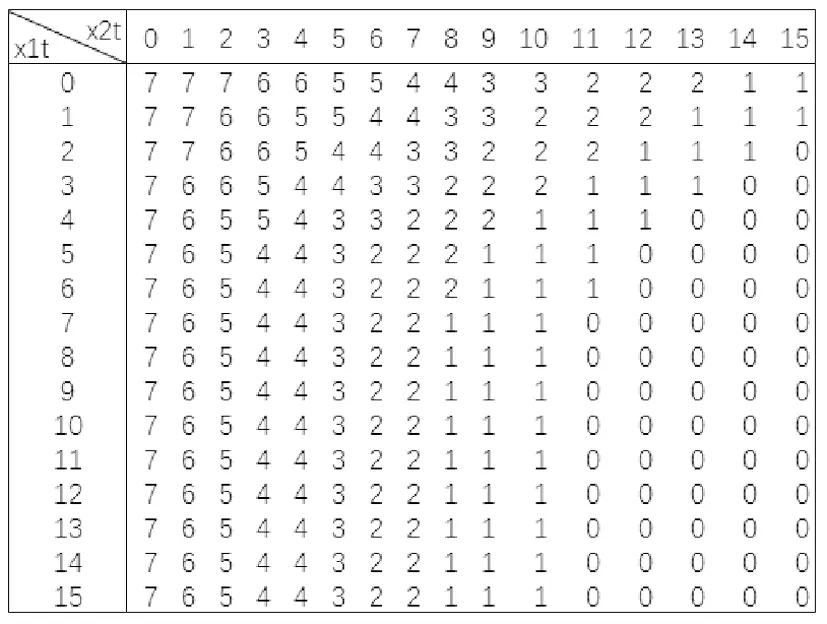
圖3 緊急需求下的最優訂貨策略(以cs=50,cl=400,r1=450,r2=450為例)

3.2.2 最優使用策略

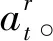
(1)若(-x1t)++at≤x2t-q2t，有y2t=(-x1t)++at。總需求(-x1t)++at小于新鮮血小板庫存x2t與額度q2t之差時，需求全部用新鮮庫存來滿足。

(2)若x2t-q2t<(-x1t)++at≤x2t-q2t+(x1t)+，有y2t=x2t-q2t。總需求(-x1t)++at大于新鮮血小板庫存x2t與額度q2t之差但小于新鮮血小板庫存x2t與額度q2t之差加陳舊血小板庫存(x1t)+時，先將新鮮血小板庫存x2t使用至額度q2t，然后剩下的需求用陳舊血小板庫存(x1t)+滿足。

(3)若x2t-q2t+(x1t)+<(-x1t)++at，有y2t=min((-x1t)++at-(x1t)+,x2t)。總需求(-x1t)++at大于新鮮血小板庫存x2t與q2t額度之差加陳舊血小板庫存(x1t)+時，先使用陳舊血小板庫存(x1t)+，剩下的需求用新鮮血小板庫存x2t滿足。

3.3 啟發式策略

(1)本文通過觀察3.2節值迭代算法求出的最優控制策略數值解的主要特征，構造近似最優的參數化啟發式控制策略如下：①近似訂貨策略為帶有訂貨下限的閾值訂貨策略。進行訂貨決策時首先將總庫存水平訂貨至一個固定的訂貨閾值TH，根據新鮮庫存x2t的不同狀態確定不同的訂貨下限，如果基于閾值的訂貨量小于x2t對應的訂貨量下限則按照該訂貨量下限進行訂貨。②近似使用策略為配額策略(Quota Policy)。假設有一個不隨狀態變化的配額q2，使用前先保留額度為q2的新鮮庫存，然后對剩余庫存采用LIFO的規則進行使用，如果剩余庫存無法滿足當期需求，最后再使用q2部分的新鮮庫存。

(2)為了對比不同訂貨策略對系統性能的影響，簡化近似策略的訂貨下限結構得到閾值訂貨策略+Quota使用策略：①進行訂貨決策時將總庫存水平(x1t+x2t)訂貨至一個固定的訂貨閾值TH。②使用策略采用配額策略，假設有一個不隨狀態變化的配額q2。

(3)為了驗證本文的近似策略相對于傳統策略的優越性，本文以Haijema等[12]中優化得到的閾值+FIFO策略進行對比。該作者根據醫院實際使用情況假設血小板使用策略為FIFO策略，并通過SDP方法平衡短缺和浪費來優化訂貨策略，優化后近似為閾值策略。閾值訂貨策略+FIFO使用策略(傳統優化策略)具體如下：①進行訂貨決策時將總庫存水平(x1t+x2t)訂貨至一個固定的訂貨閾值TH。②使用策略采用FIFO使用策略。

3.4 仿真實驗

根據3.1節中因素水平表的參數設置進行仿真實驗，分別在普通需求和緊急需求下對最優控制策略以及不同的啟發式策略進行仿真，以狀態(0,0)為初始狀態，運行100000天并輸出日均效用，其中近似策略的參數通過精英保留遺傳算法進行仿真優化，閾值+Quota以及閾值+FIFO策略的閾值通過枚舉法進行仿真優化。

遺傳算法的收斂性：對于近似啟發式策略，遺傳算法的參數設置如下：群體規模50，交叉概率0.7，變異概率0.04，最大進化代數1000。以普通需求下cs=100,cw=80,r1=400,r2=500為例，近似策略的運行時間為425s，算法所得最好值見圖4。從圖4可以看出遺傳算法在約200代時達到收斂，收斂速度較快。改變參數組合，收斂情況發生變化，但是基本在300代之前可達到收斂，少數參數組合在500代之前可達到收斂。

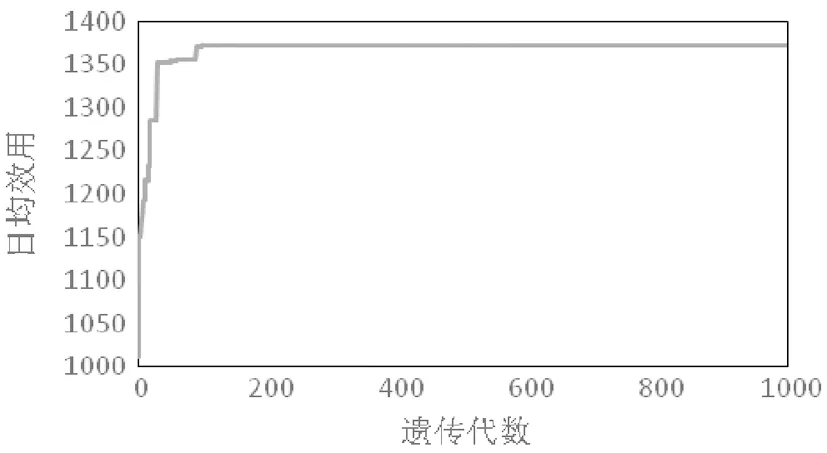
圖4 普通需求下近似策略遺傳1000代最優值收斂曲線(以cs=100,cw=80,r1=400,r2=500為例)

緊急需求和普通需求下所有參數組合在啟發式策略下的仿真結果與最優策略的Gap分別見表4和表5。觀察發現緊急需求下近似策略與最優策略的平均Gap僅有0.19%，在絕大多數情況下均可很好的近似最優策略；閾值+Quota策略與最優策略的平均Gap為2.97%，在部分參數組合下表現較好，但是其表現并不穩定，與最優策略的最大Gap可達7.53%；閾值+FIFO策略表現最差，與最優策略的最大Gap可達20.22%。普通需求下近似策略與最優策略的平均Gap僅有0.06%，在所有參數組合下均可很好的近似最優策略；閾值+Quota策略與最優策略的平均Gap為0.68%，在大部分參數組合下表現良好，但是其表現并不穩定；閾值+FIFO策略表現最差，與最優策略的最大Gap可達11.52%。

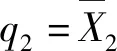
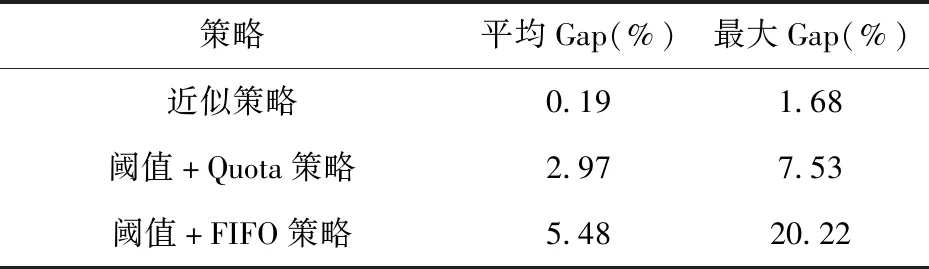
表4 緊急需求下不同啟發式策略與最優策略日均效用Gap對比

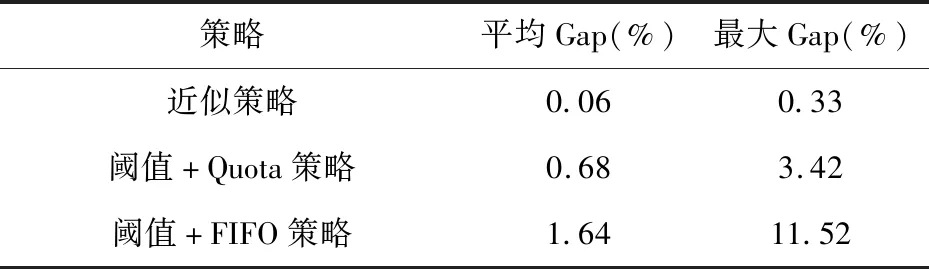
表5 普通需求下不同啟發式策略與最優策略日均效用Gap對比

圖5至圖12分別繪制了兩種需求不同因素水平下三種啟發式策略與最優策略的平均Gap對比，觀察發現：

1)觀察圖5和圖6發現隨著單位浪費成本cs的增加，近似策略與最優策略的Gap一直處于一個較低的水平，閾值+Quota策略和閾值+FIFO策略與最優策略的Gap均下降。隨著單位浪費成本的增加，閾值+FIFO策略逐漸接近閾值+Quota策略，說明單位浪費成本越高，為了避免產生浪費，滿足需求時越趨向于先使用陳舊庫存，最優使用策略越趨向于FIFO策略。對比近似策略和閾值+Quota策略，發現帶有訂貨下限的閾值訂貨策略明顯優于簡單的閾值策略。

2)觀察圖7和圖8發現隨著單位失銷成本cl和單位積壓成本cw的增加，近似策略與最優策略的Gap一直處于一個較低的水平。緊急需求下隨著單位失銷成本cl的增加，閾值+Quota策略與最優策略的Gap無明顯變化，閾值+FIFO策略與最優策略的Gap稍增；普通需求下隨著單位積壓成本cw的增加，閾值+Quota策略和閾值+FIFO策略與最優策略的Gap均增加。這說明單位短缺成本越高，帶有訂貨下限的閾值訂貨策略相對于簡單的閾值訂貨策略的優勢越明顯。

3)觀察圖9至圖12發現隨著新鮮血小板單位輸血效用r2以及不同新鮮度血小板單位輸血效用比r1/r2的增大，近似策略與最優策略的Gap一直處于一個較低的水平。隨著r2的增加，閾值+Quota和閾值+FIFO策略與最優策略的Gap均無明顯變化；隨著r1/r2的增大，不同新鮮度血小板之間的單位輸血效用差減小，閾值+Quota和閾值+FIFO策略與最優策略的Gap均明顯減小。這說明不同新鮮度血小板之間的單位輸血效用差別越大，近似策略相對于閾值+FIFO策略的優越性越明顯。隨著不同新鮮度血小板之間的單位輸血效用差的減小，最優使用策略逐漸趨向于FIFO使用策略，閾值+Quota策略和閾值+FIFO策略的Gap逐漸減小。即使不考慮不同新鮮度血小板之間的單位輸血效用差別，帶有訂貨下限的閾值訂貨策略也明顯優于簡單的閾值策略。

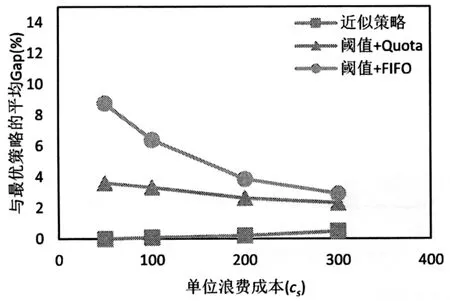
圖5 不同單位浪費成本下三種啟發式策略與最優策略的平均Gap對比(緊急需求)

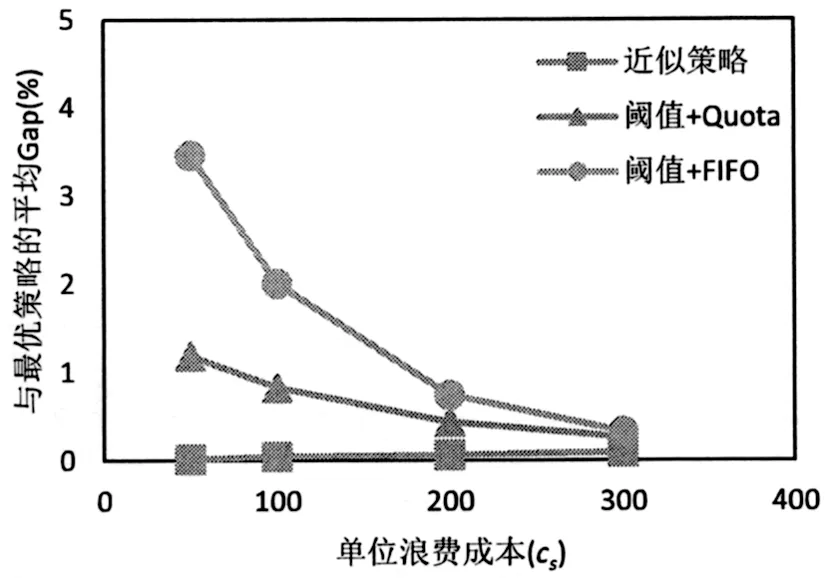
圖6 不同單位浪費成本下三種啟發式策略與最優策略的平均Gap對比(普通需求)

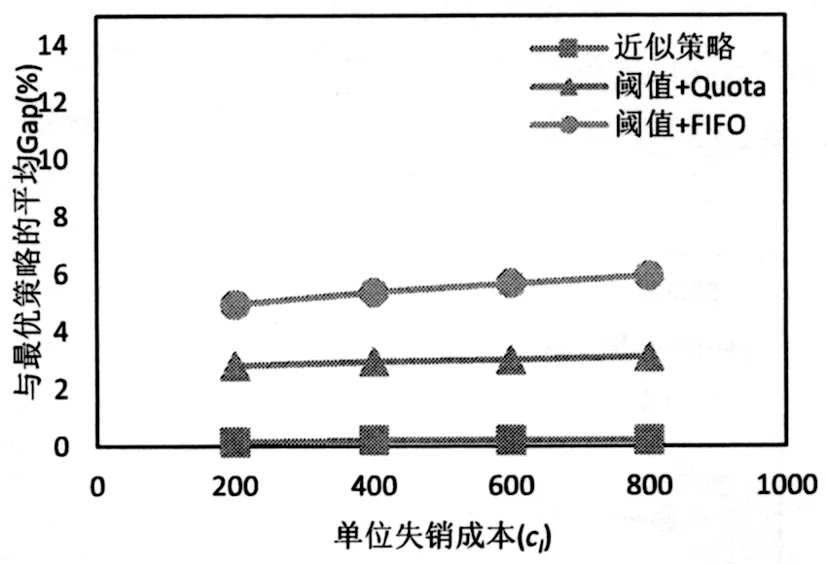
圖7 不同單位失銷成本下三種啟發式策略與最優策略的平均Gap對比(緊急需求)

圖8 不同單位積壓成本下三種啟發式策略與最優策略的平均Gap對比(普通需求)

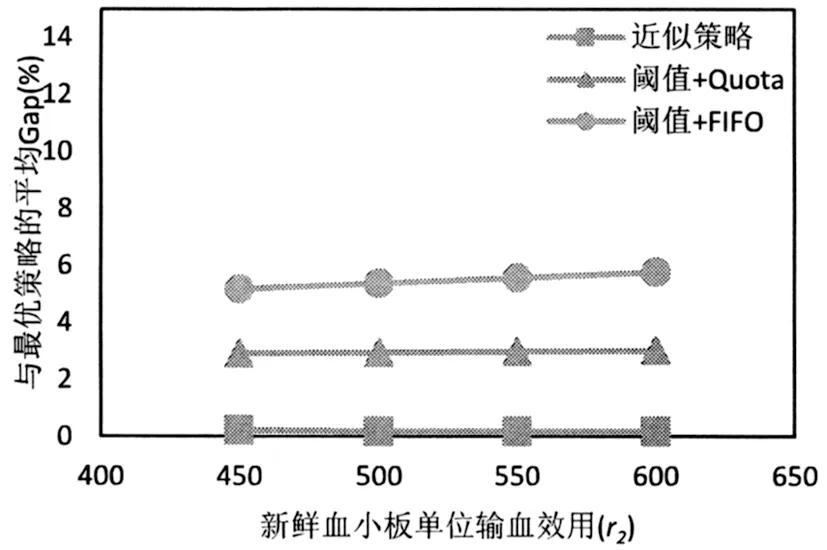
圖9 不同新鮮血小板單位輸血效用下三種啟發式策略與最優策略的平均Gap對比(緊急需求)

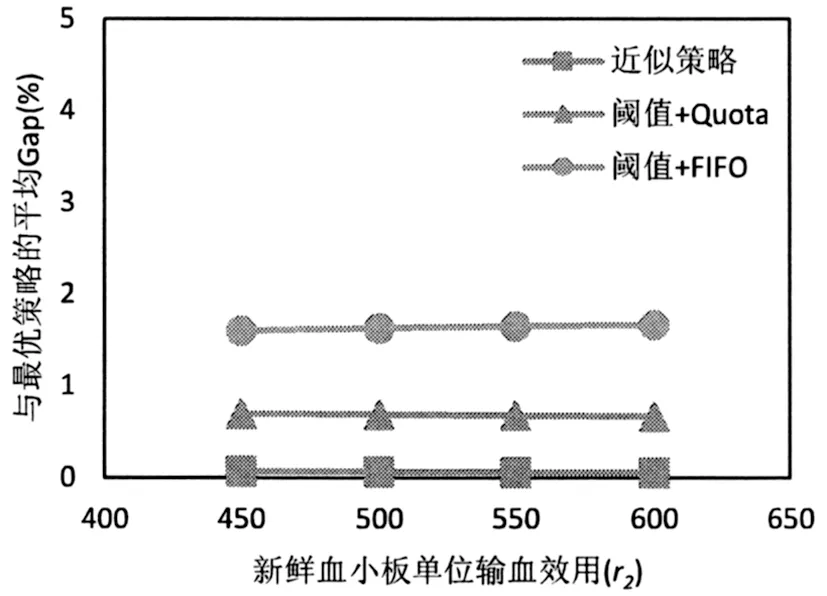
圖10 不同新鮮血小板單位輸血效用下三種啟發式策略與最優策略的平均Gap對比(普通需求)

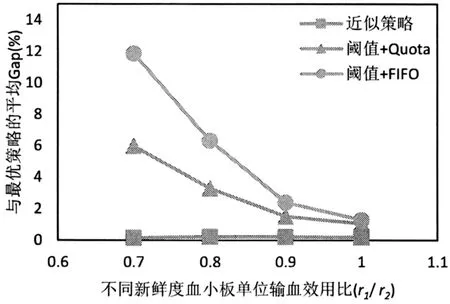
圖11 不同新鮮度血小板單位輸血效用比下三種啟發式策略與最優策略的平均Gap對比(緊急需求)

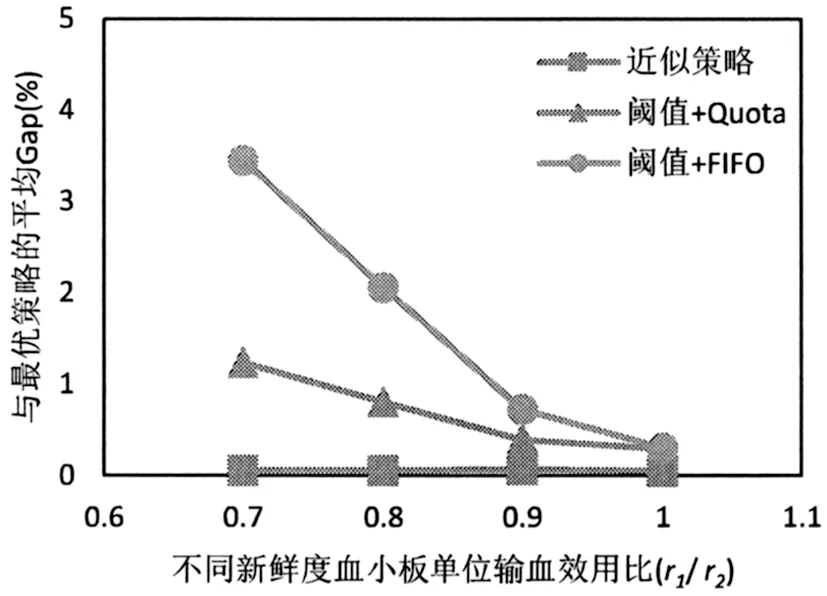
圖12 不同新鮮度血小板單位輸血效用比下三種啟發式策略與最優策略的平均Gap對比(普通需求)

圖13和圖14分別繪制了兩種需求不同需求到達率下三種啟發式策略與最優策略的Gap對比，觀察發現隨著需求到達率的增加，近似策略與最優策略的Gap一直處于一個較低的水平，閾值+Quota策略與最優策略的Gap下降，閾值+FIFO策略在兩種需求模式下均表現最差。這說明近似策略可以很好的適應不同的需求到達率，而閾值+Quota策略在需求到達率較高的情況下也是一種相對較好的策略。

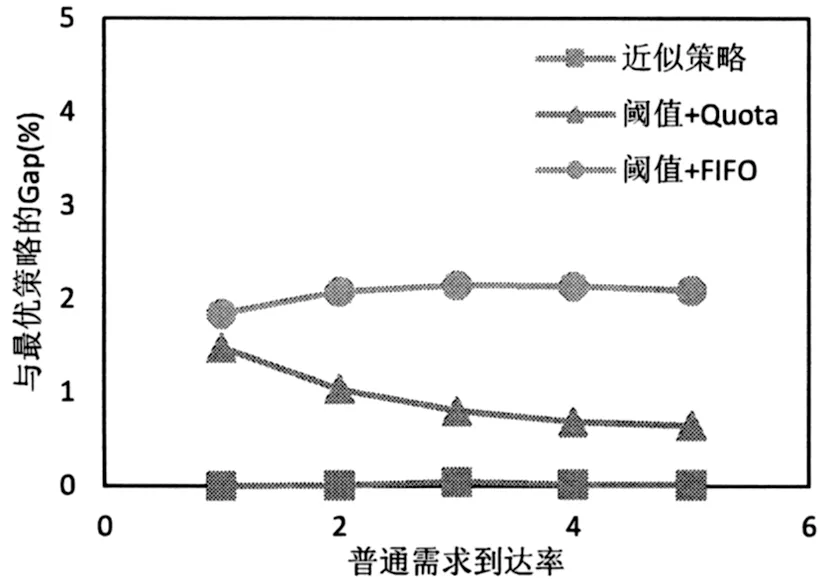
圖11 不同普通需求到達率下三種啟發式策略與最優策略的Gap對比(以cs=100,cw=80,r1=400,r2=500為例)

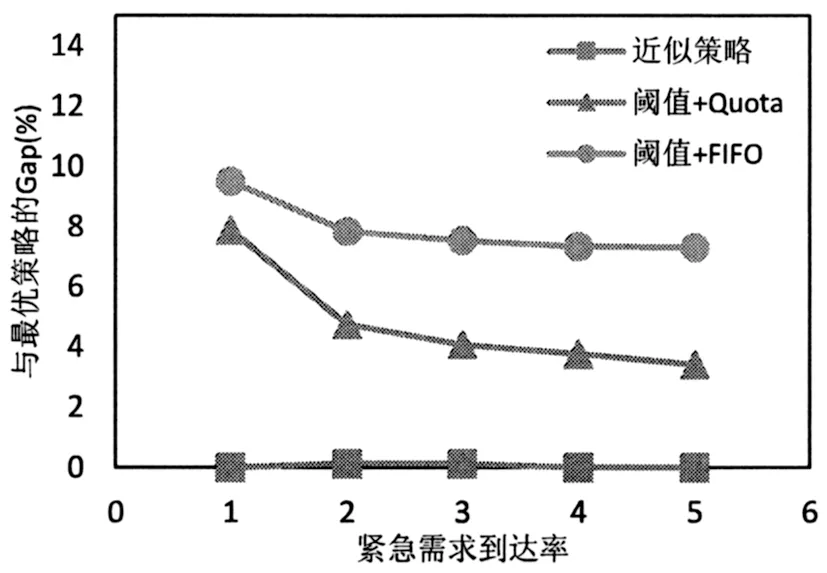
圖14 不同緊急需求到達率下三種啟發式策略與最優策略的Gap對比(以cs=100,cl=400,r1=400,r2=500為例)

4 結論

為了更合理的利用稀缺血液資源，本文研究了血小板庫存控制的訂貨和使用策略的聯合優化問題。以最小化短缺和浪費并最大化輸血效用為目標，提出了有限時域的MDP模型進行動態決策。系統每天天初根據分年齡庫存狀態進行訂貨決策，之后隨著不同需求的到達，醫院需要及時根據分年齡庫存狀態以及需求情況進行使用決策。對MDP模型的最優控制策略進行求解，發現最優訂貨策略可近似為帶有訂貨下限的閾值策略，最優使用策略為配額策略。為了便于實施，本文通過觀察最優控制策略數值解的主要特征提出了參數化啟發式控制策略，通過遺傳算法對啟發式控制策略的參數進行優化，并通過數值實驗進行驗證，發現緊急需求和普通需求下帶有訂貨下限的閾值訂貨策略明顯優于簡單的閾值策略，配額策略明顯優于FIFO使用策略。

未來的研究可結合需求到達情況考慮不同需求的混合及相互影響，將血小板的有效壽命擴展至三天并考慮不確定性供給，使得模型更加貼合實際。此外，本文模型忽略的血小板血型問題可能會對訂貨策略產生一定影響，比如相容性高的血小板如O型血可適當多訂。未來可考慮血型以及異型輸注懲罰。