異徑電磁流量傳感器權函數分布規律研究*

葛玉石， 梁利平， 徐科軍， 楊雙龍， 許 偉， 吳建平

(合肥工業大學 電氣與自動化工程學院，安徽 合肥 230009)

0 引 言

異徑電磁流量傳感器由于安裝空間狹小、前后沒有理想直管段，管道內被測流場通常是非理想流場，將導致測量值與真實值存在較大偏差、影響計量精度。為提高非理想流場的測量性能，需要研究合適的異徑截面形狀和尺寸，以提高傳感器內權函數分布的均勻度。然而國內外相關的研究較少。

Shercliff J A和Bevir M K 等人首次提出和深化了電磁流量計的權函數理論[1,2]。衛開夏等人[3]利用ANSYS有限元軟件求解非滿管電磁流量計的權函數分布。孔令富等人[4]使用MATLAB軟件中的PDE工具箱對權函數進行有限元求解。王月明等人[5]基于ANSYS對含有非導電物質時的電磁流量計進行有限元分析。李雪菁[6]采用COMSOL Multiphysics有限元軟件求解非絕緣管電磁流量計的權函數分布。王經卓等人[7,8]基于COMSOL軟件,利用流體像素的方法求解電磁流量計權函數的分布。上述文獻主要針對圓管電磁流量傳感器點電極的二維權函數進行分析，其研究結果與實際三維情況存在偏差。同時，尚未有人針對異徑電磁流量傳感器三維權函數的分布規律進行研究。由于無可參考的非理想流場測量工況的理論依據，研發人員無法確定究竟何種異徑截面有助于提高權函數均勻度，也無法確定哪一種尺寸有助于提高權函數均勻度。

針對這一問題，本文從理論上研究權函數與耦合電動勢關系，確定提高權函數分布均勻度有助于非理想流場測量。通過COMSOL軟件采用電場模擬法，分析4種不同異徑截面電磁流量傳感器的權函數分布均勻度，確定較優的異徑截面形狀。針對優選異徑截面形狀的圓電極電磁流量傳感器，研究權函數分布均勻度與異徑段長寬高之間的規律。所得結論為異徑電磁流量傳感器的測量管結構尺寸設計提供了一定的參考，也為提高異徑電磁流量傳感器的非理想流場測量性能提供了理論依據。

1 電磁流量傳感器檢測原理

當導電性液體在磁場中作切割磁力線運動時，液體中有感應電流產生。假定液體的電導率σ是均勻、各向同性的，則歐姆定律的普遍公式寫作[9]

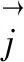
(1)

當激勵電流角頻率ω不大時，流體中的位移電流完全可以忽略，即

將式(2)帶入式(1)得電磁流量傳感器的基本測量方程

通常借助Green函數G來求解微分方程(3)，G滿足Laplace方程

根據傳感器的管道形狀和電絕緣邊界條件，建立了完整形式的電磁流量傳感器基本方程

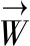
在直角坐標系(x,y,z)中，式(5)可以轉換為

UAB=?(vx,vy,vz)·((Bx,By,Bz)×(Wx,Wy,Wz))dxdydz

(6)

若磁感應強度在傳感器有效工作區間內分布均勻，則磁感應強度B=By，Bx=Bz=0，式(6)可以化為

UAB=?(vx,vy,vz)·((0,By,0)×(Wx,Wy,Wz))dxdydz

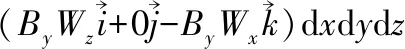
(7)

當流速為軸向流時，即v=-vz，vx=vy=0；則式(7)表示為

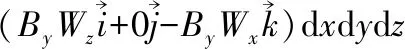
=?ByWxvzdxdydz

(8)

同時，若傳感器內的權函數分布均勻，Wx=W，則式(8)變為

UAB=ByW?vzdxdydz

(9)

傳感器內的權函數分布均勻時，感應電動勢大小只與流速積分值成正比，不依賴于流型的分布，有利于非理想流場的精確測量。

2 權函數仿真與分析

電磁流量傳感器內的流體微元切割磁力線產生感應的電勢和電位，相當于一個個微小的“電源”。某一點的權函數應為該點微元作為“電源”所產生的電位梯度與電極間電位差之比。所以，可以采用電場模擬法測定權函數：傳感器空間內充滿導電液體(一般為水)，在電極處施加一定的電壓，便會在導電介質中形成一個電場，測得各點的電場強度，并除以中心點的電場強度，即得到歸一化后的權函數值，將其繪制成等值線圖便可得到權函數分布圖。

2.1 仿真方法

2.2 結果分析

2.2.1 不同異徑面的影響

為考察不同異徑截面權函數分布的均勻性，使用上述方法對圓形、正方形、八邊形和矩形異徑截面的權函數分布進行定性分析。為了便于對比，設置管道口徑為DN100，異徑部分截面積為3 200 mm2。所以，圓形異徑面半徑為32 mm，正方形異徑面邊長為56.6 mm，八邊形異徑面邊長為25.8 mm，矩形異徑面長寬為80×40 mm。仿真結果如圖1所示，為了便于對比，權函數等勢線大小從0開始，以0.25為步長遞增到30。由圖1(a)～圖1(d)可知，矩形異徑截面的權函數等勢線間距最大，即權函數變化梯度最小，權函數分布最均勻。

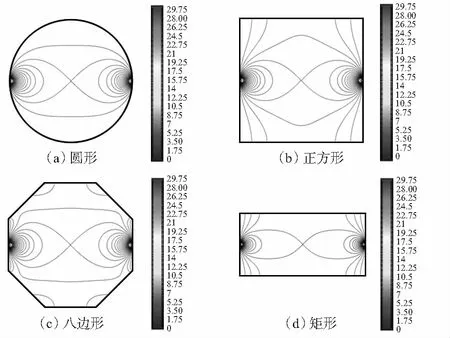
圖1 不同異徑截面的權函數分布

為了客觀評價不同異徑截面內權函數分布的均勻程度，采用整體均勻度來定量衡量權函數的均勻性，設電極截面內每個節點的權函數值為Wk，相應截面的權函數平均值為W0，則電極截面內權函數的整體均勻度R為

通過式(10)計算得到圓形、正方形、八邊形、矩形4種不同異徑截面權函數分布的整體均勻度分別為1.811 2，1.996 9，1.915 0，1.563 9。

綜上所述，矩形異徑結構的權函數分布最均勻，所以，異徑電磁流量傳感器采用矩形異徑的管道結構，該結構權函數分布比較均勻，能夠減少非理想流場引入的測量誤差。在實際生產實踐過程中，權函數分布與矩形段長L、寬D、高H有關，因此，開展了矩形異徑圓電極電磁流量傳感器的三維權函數建模分析，最終得到一種權函數分布比較均勻的結構尺寸。

2.2.2 三維權函數分布

使用Pro/E軟件建立三維幾何模型，導入COMSOL軟件進行有限元求解。仿真模型如圖2所示，電極連線為x軸，連線中點為坐標原點，流體運動方向為z軸，傳感器管道口徑為DN100，總長250 mm[10]。異徑管部分初始結構尺寸L=80 mm，D=80 mm，H=40 mm，圓形電極半徑為17 mm，伸出絕緣襯里的最大距離為1.5 mm。

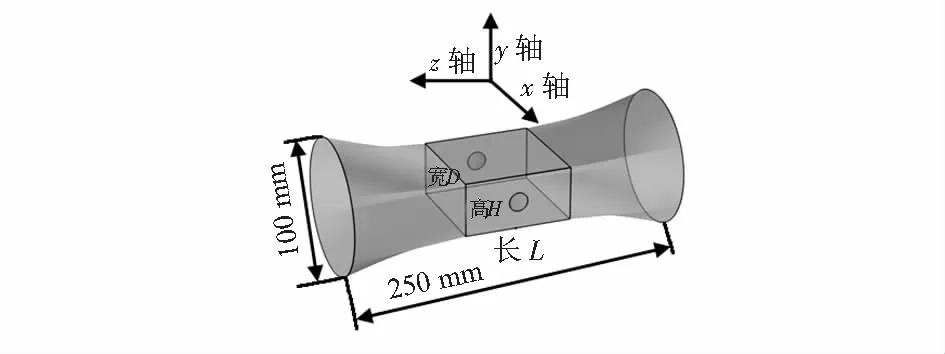
圖2 仿真模型示意

1)長度的影響

首先分析一定D×H條件下，L變化時傳感器內的權函數分布情況。由于傳感器異徑管部分高度H越小信號越強，但壓損也越大，因此，H設置為30～50 mm；異徑管寬度D越大壓損越小，但寬度越大傳感器體積也越大，所以，D設置為60～90 mm；異徑管段上下需要放置激勵線圈，同時異徑段前后需要有一定長度的過渡段來穩定流型，因此，L設置為60～120 mm。一共分析了6組D×H尺寸的傳感器權函數分布隨L的變化情況，如表2所示。由于電極截面內的權函數分布對感應電動勢影響最大，因此，利用式(10)計算電極截面xy平面內的權函數整體均勻度R。定義相同D×H條件下，權函數均勻度隨L變化的波動率為ML，如下

計算多組相同D×H、不同L時xy平面的權函數整體均勻度R及波動率ML，如表1所示。

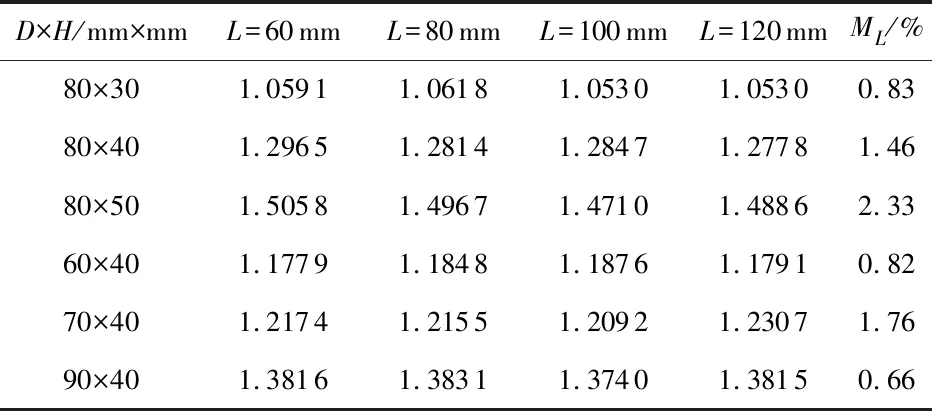
表1 多組D×H參數在L變化時的整體均勻度R和波動率ML

通過表1分析可知，隨著L的變化，權函數波動率ML≤±2.5 %，所以xy平面內的權函數整體均勻度變化較小，即長度L對電極截面內的權函數分布影響很小。

2)寬度和高度的影響

通過上述分析可知，L對傳感器內的權函數分布影響很小，因此固定設置L為80 mm。然后分析異徑段D，H同時變化時的權函數分布情況。由上節可知，矩形異徑截面的D設置為60～90 mm，H設置為30～50 mm。為了便于分析三維權函數與D，H的變化關系，設置H與D變化步長都是10 mm，因此，H變化范圍為30～60 mm，即D={60，70，80，90 mm}，H={30，40，50，60 mm}，一共16組異徑電磁流量傳感器結構。

分別對上述結構進行有限元分析，根據式(10)計算xy平面內權函數整體均勻度R，根據式(11)計算權函數隨H變化的波動率MH，隨D變化的波動率MD，結果如表2所示。

表2 D和H同時變化時的權函數整體均勻度及波動率

根據表1和表2權函數均勻度的波動率數值可以看出，MH>MD>ML，所以，矩形段L，D，H對于權函數均勻度的影響程度是依次增強的，高度H對權函數均勻度影響最大，寬度D影響稍小，長度L影響很小。且D和H越小，權函數整體均勻度R越小，權函數分布越均勻。

為了更加全面地比較權函數在三維空間的分布情況，從上述結構中選取D×H={90×30，60×30，60×60}三組典型結構，分析其權函數在xy，xz，yz三個平面內的分布情況。為了便于對比，統一規定三個平面內等勢線的分布步長和數值范圍：1)xy，xz平面內的權函數等勢線大小以0.25為步長，從0增加到30； 2)由于yz平面的權函數小于1，規定yz平面內的權函數等勢線大小以0.05為步長，從0增加到1。具體如圖3～圖5所示。

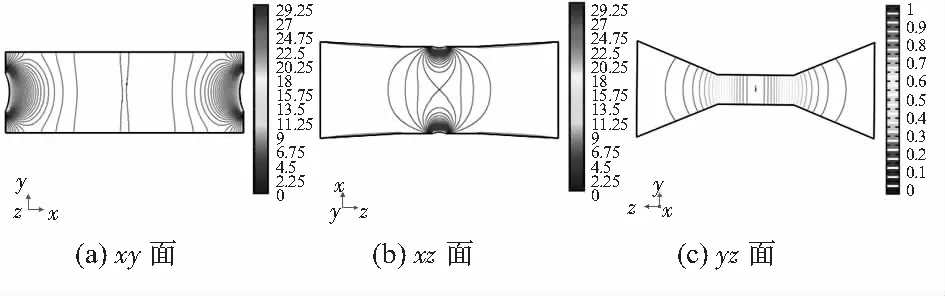
圖3 D×H=90 mm×30 mm(L=80 mm)不同截面權函數分布

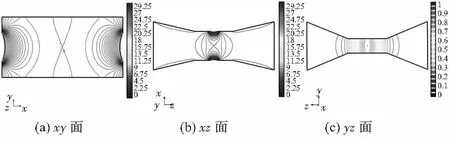
圖4 D×H=60 mm×30 mm(L=80mm)不同截面權函數分布

圖5 D×H=60 mm×60 mm(L=80mm)不同截面權函數分布

通過對圖3～圖5分析得出以下結論：

1)圖3(a)、圖4(a)的xy面權函數分布表明，D=90 mm時中心區域的權函數等勢線間距較大，即權函數變化梯度較小，且中心區域的權函數等勢線逐漸變為直線，因此中心區域的權函數分布更均勻；但D=90 mm時，電極附近的權函數等勢線較密，且等勢線顏色較深，權函數最大值較大，變化梯度較大，所以,電極附近的權函數分布均勻性較差。因為難以直接衡量D改變時，xy面權函數分布的均勻性。所以，需要利用權函數整體均勻度R定量確定xy平面內權函數分布的均勻性。結果表明，隨著寬度D的減小，權函數分布越來越均勻。

2)圖4(a)、圖5(a)的xy面權函數分布表明，H=30 mm時中心區域的權函數等勢線間距較大，且中心區域的權函數等勢線逐漸變為直線；電極附近的權函數等勢線比較稀疏，且等勢線顏色較淺，權函數最大值較小，變化梯度小，因此,H=30 mm時xy面的權函數分布更加均勻。

3)圖3(b)～5(b)的xz面權函數分布表明，三組異徑結構的權函數分布情況類似，沒有明顯的區別，即D和H的變化對xz面的權函數分布影響較小。

4)圖3(c)、圖4(c)的yz面權函數分布表明，D=90 mm時的權函數等勢線間距略大于D=60 mm時的權函數等勢線間距，權函數變化梯度較小，且中心區域的權函數等勢線逐漸變為直線，因此D=90 mm的權函數分布更均勻一些，但是兩者區別很小，即寬度改變對yz面權函數分布影響很小。圖4(c)、圖5(c)的yz面權函數分布表明，H=30 mm時的權函數等勢線間距較大，且中心區域的權函數等勢線逐漸變為直線，因此H=30 mm的權函數分布更加均勻；

5)圖3(a)～5(a)和圖3(b)～5(b)權函數分布結果表明，越靠近電極，等勢線顏色越深，即權函數值越大，且越靠近電極，權函數等勢線越密集，即權函數變化梯度越大。

綜上所述，異徑電磁水表異徑段長度L對權函數分布的均勻性影響很小，隨著長度L的改變，權函數分布基本沒有變化；異徑段高度H對權函數分布的均勻性影響最大，寬度D影響稍小，高度和寬度越小，權函數分布越均勻，即異徑電磁流量傳感器的測量精確度受非理想流場的影響越小。

3 結 論

1)圓形、正方形、八邊形和矩形等4種異徑電磁流量傳感器的權函數分析結果表明，矩形異徑截面傳感器的權函數分布最均勻。

2)電極附近區域，權函數值較大，且權函數變化梯度較大，隨著遠離電極，權函數值越來越小，且權函數變化梯度越來越小。

3)矩形段高度H對權函數分布的均勻性影響最大，隨著H的減小，權函數分布越來越均勻，且y軸權函數的分布逐漸趨近于常數1。矩形段寬度D對權函數分布的均勻性影響稍小，隨著D的減小，權函數分布越來越均勻。矩形段長度L對傳感器內的權函數分布影響很小，隨著L的改變，權函數分布沒有明顯變化。