拉脫法測試—多孔錨具咬合力試驗及分析

周建明 張峰 王大偉

摘? 要：為了研究多孔錨具內圈和外圈錐孔的夾片咬合力對拉脫法測試結果的影響，設計了室內測試夾片咬合力的試驗方案，并基于12孔錨具開展了大規模的咬合力試驗測試，共測試360個樣本，對每個錐孔的咬合力分別開展概率統計，分析內圈錐孔和外圈錐孔的咬合力差異。同時對整體的內圈和外圈的咬合力測試結果進行概率統計。研究結果表明：拉脫法典型測試曲線中可通過最高點的值減去夾片咬合力得到最終的錨下有效預應力;不管是內圈錐孔還是外圈錐孔，夾片咬合力的測試結果服從對數正態概率分布;外圈咬合力要大于內圈，比值為1.125。

關鍵詞：橋梁工程;拉脫法;;概率統計;對數正態分布;樣本

1? 引言

預應力錨固技術自問世以來，發展十分迅速，廣泛應用于土木工程領域，成為設計內容的一部分。其快速高效的社會效益和經濟效益，在加快工期與提高穩定性等方面優越性，是其他傳統方法不能替代的[1-3]。橋梁工程中大量使用預應力錨固技術，至2018年中國有約83萬座橋梁，其中預應力混凝土梁橋占到90%，歐美國家的預應力混凝土梁橋也占到70%。但是已有的大跨預應力混凝土梁橋均發生了不同程度的開裂下撓。Ba?ant Z P 等[4， 5]分析了KB bridge的開裂下撓特性，重點比較了不同的徐變計算模型對橋梁開裂和下撓的影響。在橋梁施工過程中，錨下有效預應力不足[6][7][8]是導致梁體開裂及下撓的主要原因。Yang I H 等[9]、Guo T等[10]及張運濤等[11]均采用隨機有限元并結合實測值開展了橋梁長期變形的影響分析，研究結果均表明：預應力值顯著影響橋梁的變形特性。

國內外研究人員對于鋼絞線錨下預應力進行了深入研究。宋杰等[12]采用磁通量法對廣東省博物館新館主桁架的拉索進行了索力檢測。磁通量傳感器的測試價格較高，且在橋梁體內束測試中存在安裝困難的問題。類似可以采用基于振弦原理的穿心式壓力傳感器測試預應力鋼絞線錨下預應力，但是其同樣存在測試成本高，測試樣本少。

拉脫法作為一種預應力無損檢測技術[13]，不僅可以準確測試鋼絞線錨下有效預應力，且容易實施。拉脫法基本原理為：施工期通過反拉鋼絞線使得夾片錨具的夾片脫開，并以此刻測試得到的張拉力作為錨下有效預應力值。BRUCEM首次使用拉脫法測試了大壩的錨索有效張拉力，由于拉脫法的測試精度高， Zhang Peng等[14]的研究測試方案也類似。拉脫法在邊坡、大壩錨索檢測時由于采用整體反拉方案，張拉力和延伸量的典型曲線均為兩折線組成。在橋梁工程中應用時對單根鋼絞線進行反拉，發現張拉力-延伸量曲線斜率在張拉力達到最高點時發生突變[15， 16]。究其原因，在鋼絞線張拉時，夾片與錨具發生擠壓，產生摩擦力，導致鋼絞線在反拉過程中，需克服這種力，從而在測試中發生張拉力的突變。反拉過程中，錨杯對夾片和鋼絞線的彈性擠壓作用導致“咬合力”。需要注意的是：拉脫法測試技術是專門針對夾片錨的一種測試技術，橋梁工程中大量存在多孔錨具，多孔錨具的外圈錐孔和內圈錐孔周邊的錨杯構造存在差異，因此受到的荷載效應可能會有差異，如何判別這種不同的荷載效應對夾片咬合力的影響，目前的研究還是空白。

本研究設計了錨下預應力及錨外張拉力同步測試的試驗方案，對多孔錨具的預應力鋼絞線開展測試，基于統計學原理獲得了外圈錐孔的夾片咬合力和內圈錐孔的夾片咬合力的差異，為后續的拉脫法進一步推廣應用提供了理論參考。

2? 咬合力試驗測試

拉脫法典型測試曲線。

拉脫法測試典型曲線如圖 1，在鋼絞線延伸量到達一定數值時，鋼絞線張拉力會發生突然下降（圖 1AB段）。

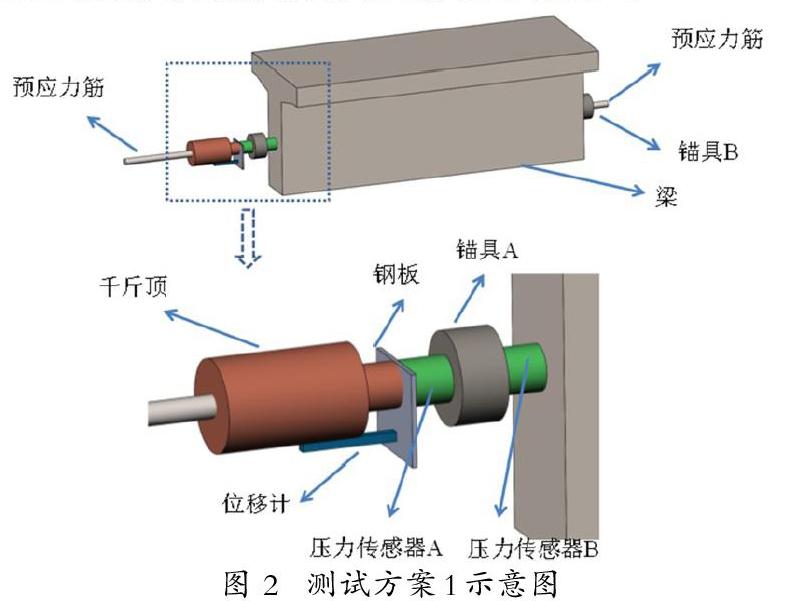
拉脫法的測試結果僅僅代表錨具外露段鋼絞線的張拉力。課題組通過大量的現場測試，測試方案具體參見圖 2。

課題組在橋梁現場測試的樣本曲線如圖 3。

分析圖 3中錨下預應力和錨外張拉力時程曲線，測試曲線可簡化為圖 4的表示。曲線取5個特征點，其中A點為錨外峰值點，B點為錨外突變段的低谷點，C點為錨下有效預應力點，D點為錨下瞬態內力重分布的峰值點，E點為拉脫法測試結束后的錨下預應力點。

分析圖 4可以認為：AB段為拉脫法測試曲線的突變段，而AC段才是夾片咬合力區段。由于C點為錨下有效預應力值，因此，通過拉脫法測試曲線的A點獲得C點，必須統計咬合力AC段。

3? 多孔錨具咬合力測試

第一部分已介紹了咬合力的測試結果對拉脫法測試的重要性，本節將進一步描述多孔錨具的不同位置錐孔的咬合力測試差異。

3.1? ?錨具尺寸

本次研究采用12孔標準錨具進行測試，錨具尺寸參見

錨具厚度為60.3mm。

3.2? ?測試方案2

測試方案1需要在現場進行反復張拉和退錨，試驗操作較為復雜，且退錨操作具有一定的安全隱患。因此，本研究進一步提出了測試方案2。該方案為室內試驗，試驗步驟為：

①編號

給所有錐形孔道編號，外圈孔道為1-9，內側孔道為10-12。

②張拉錨具所有錐形孔道

張拉錨具所有錐形孔道，張拉力為100kN。第一步張拉位置為錐孔狹窄位置（圖 7a）。

③反拉和數據采集

反拉時，提前在反拉位置安裝好電阻式壓力傳感器。

8? 反拉操作

使用智能無線采集設備采集咬合力。

4? 數據分析及整理

4.1? 測試樣本數據

錨具的12個錐孔均測試10個咬合力，共計測試3個錨具（編號：A/B/C）。

外圈鋼絞線和內圈鋼絞線分別采集。咬合力分別采集30組數據，共360個咬合力樣本。1-10號錐孔（內圈）的鋼絞線張拉力和咬合力測試結果參見表1。表中的F為第一步的張拉力，M為咬合力測試結果。

由于實際試驗時，第一步張拉時，千斤頂的張拉力無法準確保證張拉力為100kN。考慮到張拉力和咬合力兩者之間為線性函數關系，即：

M=kF

式中：

k——為標定常數。

根據表達式（1），則所有樣本的咬合力均可換算成設計張拉噸位195k N時的咬合力。后續分析時，咬合力的測試結果均為張拉力195k N時，修正表中測試數據的結果。

以錐孔1為例，基于30個測試樣本分別統計正態、對數正態和威布爾分布的累積概率密度圖。

分析圖 10可以看出：對數正態分布的統計結果和測試樣本更為吻合。

后續12個錐孔的數據均按照對數正態分布進行統計（圖 11）。限于篇幅，僅僅列出幾個樣本的數據。

在概率論與統計學中，對數正態分布是對數為正態分布的任意隨機變量的概率分布。如果X是對數正態分布，則lnX為正態分布。對于x> 0，對數正態分布的概率密度函數為

進一步統計每個錐孔的30個樣本（共計360個樣本）的對數正態分布的期望值。具體參見表2，表2中，第一列為樣本測試值的對數，第二列為樣本測試值對數值的方差，第三列為對數正態分布的期望值。

進一步統計1-9號錐孔的統計均值，得到外圈咬合力均值為29.32kN，內圈咬合力均值為26.06kN。外圈咬合力要大于內圈，比值為1.125。

5? 結束語

（1）拉脫法典型測試曲線中可通過最高點的值減去夾片咬合力得到最終的錨下有效預應力。

（2）不管內圈錐孔還是外圈錐孔，夾片咬合力的測試結果服從對數正態概率分布。

（3）通過360個樣本的概率統計測試，研究認為外圈咬合力要大于內圈，比值為1.125。

參考文獻：

[1] 張雄，陳勝宏.預應力錨索內錨段復合單元模型研究[J].巖土力學，2012（3）：933～938.

[2] 王凌波，鄭斐.內置勁性骨架的PC箱梁橋合龍段時變性能分析[J].中國公路學報，2015（4）：69～75.

[3] 張運濤，孟少平.基于響應面法的大跨連續剛構橋長期變形預測[J].土木工程學報，2011（8）：102～106.

[4] 宋杰，陳魯，張其林，等.磁通量法在預應力懸掛結構拉索施工中的應用[J].振動、測試與診斷，2009（1）：86～91.

作者簡介：

周建明（1976—）男，漢族，江蘇姜堰人，本科，中鐵十局集團第一工程有限公司總經理、黨委副書記，高級工程師。

通訊作者簡介：

張峰（1978—）男，江蘇泰州人，教授，博士生導師。