復雜場景下的ETC系統路徑損耗研究*
何怡剛, 張超群, 李 兵, 佘培亮, 蘇蓓蕾, 許 越
(合肥工業大學 電氣與自動化工程學院,安徽 合肥 230009)
0 引 言
無源超高頻(ultra high frequency,UHF)的射頻識別(radio frequency identification,RFID)技術是一種基于無線射頻通信方式的自動識別技術,具有識別距離遠、功耗低、操作快等特點,在智能物流領域應用廣泛[1,2]。通過RFID技術,ETC系統中的車載單元(on-board unit,OBU)和路側單元(rood side unit,RSU)可實現車輛的自動識別和相關數據交換,從而實現電子不停車收費(electronic toll collection,ETC),大大提高收費效率[3,4]。考慮到復雜場景下的諸多因素都會影響電磁波在信道中的傳播效率,因此,有必要考慮信道傳播的路徑損耗和實際應用場景下的多徑傳播。
文獻[5]首次提出了移動散射體下的V2V無線信道傳播模型,并且計算得到模型的自相關函數和多普勒功率譜密度等。文獻[6]分析了無線攜能通信在無線傳感器網絡中應用,驗證了方法能有效提高無線通信傳播的效率。文獻[7]主要針對不同頻率的電磁波穿透車輛時造成的路徑損耗進行了研究,但未考慮反射路徑損耗和自由空間損耗等影響因素。文獻[8]給出了無源超高頻RFID系統在實際應用中的鏈路預算模型,但方法的精度不足以滿足實際應用需求。文獻[9]考慮不同車輛的外形差異對路徑傳播的影響,提出了一種基于兩徑模型的ETC系統信道傳播損耗評估方法,但只考慮了單車道并且沒有前車干擾的情況。文獻[10]對多標簽環境下RFID的前后向鏈路進行了研究,對于確定閱讀器的位置以及提高標簽的讀取效率有著重要意義。文獻[11]提出一種基于光線跟蹤和射線均勻理論(uniform theory of diffraction,UTD)的ETC系統傳播損耗模型,但沒有考慮車道環境的復雜性。文獻[12]提出一種基于場景幾何特征的標簽識別范圍預測方法,對ETC多車道情形進行了分析,但對于旁道車輛與閱讀器天線及被識別車輛的距離以及不同旁道車輛造成的損耗差異沒有做出詳細的分析。
考慮在多車道情形下,旁道大型車輛與閱讀器天線及被識別車輛的距離等都會對信道傳播造成不同程度的干擾,因此,通過分析多徑射線波的幾何特征,提出了一種ETC系統的信道傳播損耗模型。
1 ETC系統場景與多徑傳播分析
目前,ETC系統的應用場景并不復雜,其與手動收費系統共存于國內外的收費廣場中。為確保所有類型帶有OBU的車輛均能順利通過,RSU應具有足夠大的通信范圍,而在多車道情形下,RSU與被識別車輛之間的通信會受到旁道車輛的干擾。將小轎車作為被識別車輛,分析旁道車輛以及前方地面或引擎蓋對系統信道傳播的影響。為便于分析,對ETC場景做出幾點說明:1)假設小轎車所在車道前方無其他車輛,即不考慮前車的影響;2)由于車輛以較低速度(10 km/h)通過收費廣場,因此不考慮車輛移動引起的路徑損耗;3)不考慮由于特殊天氣造成的路徑損耗。
典型ETC系統示意圖如圖1所示。將閱讀器天線作為參考點,被識別車輛與閱讀器天線之間的直射分量毫無遮擋,為主要傳播分量。由于兩側車輛對被識別車輛造成的影響情況相同,因此只需對一側大型車輛進行分析。旁道的大型車輛與閱讀器天線以及被識別車輛的距離分別為l和l1,被識別車輛進入可識別區域時,會接收到閱讀器天線發出的直射信號、前方地面或引擎蓋的反射信號以及旁道大型車輛的反射信號與繞射信號。

圖1 ETC場景示意
2 ETC系統信道傳播損耗評估方法
2.1 ETC系統傳播機制
2.1.1 地面或引擎蓋的反射路徑
假設RSU的高度為H,OBU的高度為h,將RSU與被識別車輛的水平距離設為d,隨著距離d的變化,反射路徑會有所不同。RSU與OBU的直接距離為
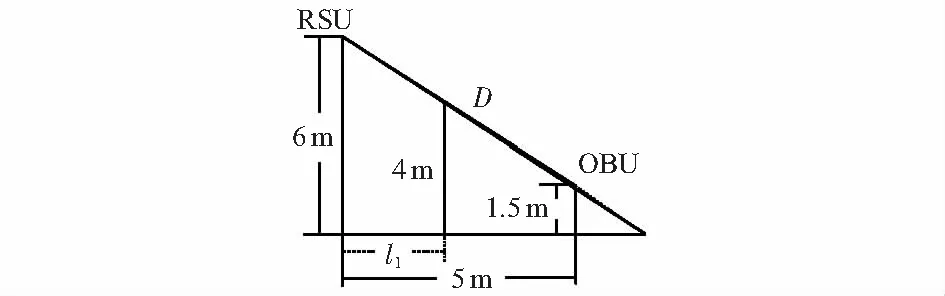
如圖2所示,將地面或引擎蓋的一次反射路徑距離設為
當0 當d1 當d2 根據三角形相似原理可以得出 圖2 小轎車反射路徑 參考實際情況確定ETC場景的幾何參數,閱讀器天線高度H為6 m,被識別車輛高度h為1.5 m,小轎車引擎蓋高度h1為0.75 m,車頭與標簽距離L0為1 m,天線可識別距離d3為15 m。 2.1.2 旁道車輛的反射路徑 在多車道情形下,旁道車輛與被識別車輛的距離較近,所以旁道車輛引起的反射路徑會對系統的信道傳播產生影響。文獻[13]中提出ETC系統路徑損耗的影響因素主要是周圍的一次反射路徑,所以接下來討論旁道車輛的一次反射幾何關系。 如圖3所示,將閱讀器天線坐標設置為R(0,0,H),被識別車輛O坐標為(0,d+L0,h),旁道車輛與被識別車輛的水平距離為l。 圖3 旁道車輛的一次反射幾何關系 因此x=-l為旁道車輛對被識別車輛的一次反射面,且R關于反射面的鏡像坐標為R1(-2l,0,H),旁道車輛的一次反射路徑距離為 由此可得 隨著距離l的增大,旁道車輛引起的一次反射路徑影響越來越小,當距離到達臨界值l0=5 m時,旁道車輛的反射路徑可以忽略。 2.1.3 旁道車輛的繞射路徑 假設被識別車輛與閱讀器天線的距離d=4 m,分析旁道車輛引起的一次繞射路徑,繞射點與閱讀器天線的水平距離為l1,與被識別車輛的水平距離為l2,有以下關系 l1+l2=d+L0=5 m (9) 假設旁道車輛是高度為4 m的貨車,一次繞射路徑可以看作單刃峰繞射,因此繞射常數[13]為 式中 ΔH為繞射點的等效高度,即RSU與OBU的連線與貨車最高點D的高度差。 如圖4所示,繞射點D的高度為4 m,由幾何分析可得 ΔH=2-0.9l1 (11) 當ΔH=0時,l1=20/9 m,因此:當繞射點0 圖4 等效高度示意 ETC系統路徑損耗可表示為 L=PO/PR (13) 式中L為路徑損耗,P0為OBU接收功率,PR為RSU發射功率。 在設定的場景中,ETC系統的路徑損耗包括自由空間損耗、一次反射路徑損耗、一次繞射路徑損耗以及汽車前擋風玻璃的穿透損耗等,取玻璃的穿透損耗Lα=2.7 dB,一次繞射路徑損耗已由式(12)給出,其余路徑損耗的具體分析如下: 自由空間損耗 式中λ為波長,k為波數,dd為直射路徑R-O的傳輸距離。 地面或引擎蓋的反射路徑損耗 式中dr為反射路徑R-A-O的傳輸距離,Γr1和Γr2分別為地面和引擎蓋的反射系數。 旁道車輛的反射路徑損耗 式中dl為反射路徑R-P-O的傳輸距離,Γr3和Γr4分別為旁道大型車輛即客車或貨車側身的反射系數。 反射系數由參考文獻[12]可得 式中εr為反射面相對介電常數,α為入射波與反射面之間的夾角。 2.3.1 OBU與RSU距離對路徑損耗的影響 首先分析被識別車輛前方的路徑損耗,即自由空間損耗和地面或引擎蓋引起的一次反射路徑損耗。取車輛的穿透損耗為23.8 dB,假定旁道車輛與閱讀器天線的水平距離l1=3 m,與被識別車輛的水平距離l=2 m,此時ETC系統路徑損耗只跟RSU和OBU的距離有關,因此可表示為 (18) 2.3.2 旁道車輛的位置對路徑損耗的影響 分析旁道車輛對被識別車輛造成的一次反射路徑損耗和一次繞射路徑損耗,假定被識別車輛與閱讀器天線的水平距離d=4 m,此時可以確定自由空間損耗和由地面引起的一次反射路徑損耗,ETC系統路徑損耗隨旁道車輛的位置變化而變化,因此可表示為 (19) 根據上述分析得出在ETC系統信道傳播中,引起路徑損耗變化的因素主要是RSU與OBU的距離d、旁道車輛與RSU的距離l1、旁道車輛與OBU的距離l。通過給出的ETC系統路徑損耗模型進行仿真模擬,分析3個變量對系統的影響。 圖5(a)是當旁道車輛的坐標位置發生變化時,ETC系統路徑損耗變化的三維圖。圖中可以看出旁道車輛與OBU的距離l的變化沒有引起ETC系統路徑損耗的變化。圖5(b)是當RSU與OBU的水平距離d以及臨道車輛與RSU的水平距離l1同時變化時,ETC系統路徑損耗變化的三維圖。圖中可以看出:隨著距離d的增大,地面的反射損耗呈線性增大;而隨著距離l1的變化,繞射系數發生變化,從而引起系統繞射損耗的大幅度變化。 圖5 ETC系統路徑損耗變化的三維圖 確定RSU與OBU的水平距離d=4 m,旁道車輛與OBU的水平距離l取不同值時,ETC系統路徑損耗隨旁道車輛與RSU的水平距離變化的評估預測如圖6(a)所示。觀察可知,距離l取不同值時,三條曲線幾乎重疊,所以圖形的波動主要受系統的繞射損耗影響。當0 L0=20lg(0.5e0.45v)和L0=20lg(0.5+0.62v) 對其進行求導,前者導數小于后者導數,所以在點l1=20/9m處圖形不平滑。 旁道車輛與RSU的水平距離l1取不同值時,ETC系統路徑損耗隨旁道車輛與OBU的水平距離變化的評估預測如圖6(b)所示。圖中可以看出當l變化時,ETC系統路徑損耗變化非常平緩,基本控制在1 dB內,結合圖6(a)可以說明旁道車輛引起的反射路徑對系統路徑損耗的影響可以忽略。這是因為旁道車輛與OBU的水平距離l不會使反射路徑R-P-O引起明顯變化。實驗中距離l1的取值每增加0.5 m,系統的路徑損耗分別增加了4 dB和9 dB,結合圖6(a)分析,當距離2 圖6 距離l和l1變化對系統的影響 旁道車輛位于不同位置時,ETC系統路徑損耗隨RSU與OBU之間距離變化的評估預測如圖7所示。結合以上分析可知,l=2 m,l1=3 m和l=3 m,l1=3 m相對應的兩條曲線重疊,說明當l1不變,l取不同值時,路徑損耗沒有明顯變化;而當l一定,l1取不同值時,路徑損耗變化幅度明顯。根據圖7的變化趨勢可以得出,RSU與OBU的水平距離d每增加1 m,ETC系統路徑損耗增加約1 dB;旁道車輛與RSU的水平距離l1增加1 m時,ETC系統路徑損耗增加了9 dB,所以被識別車輛前方的路徑損耗和旁道車輛引起的繞射路徑損耗是影響ETC系統路徑損耗的主要因素。 圖7 距離l和l1同時變化對系統的影響 對于本文特定場景的仿真結果可以得出:旁道車輛與RSU的距離為0.6 m且被識別車輛與RSU的距離越小時,系統的路徑損耗越小。由于該評估方法忽略了前方車輛的影響,下一步將研究前方車輛和旁道車輛對系統的綜合影響。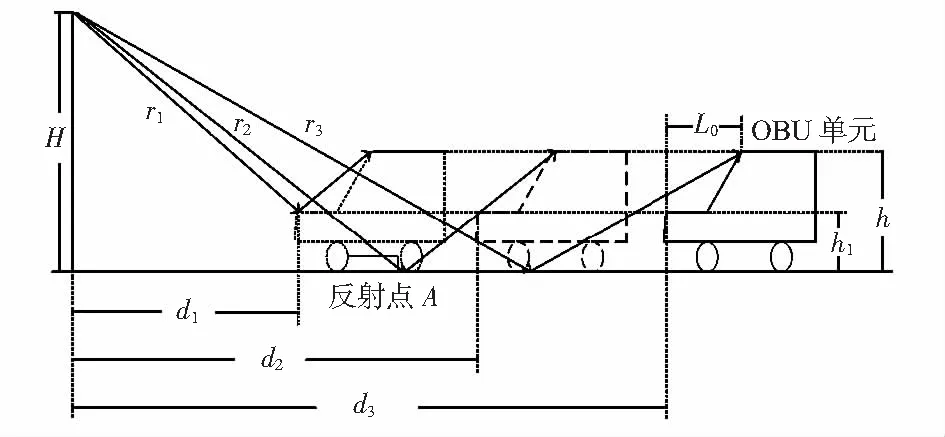

2.2 電磁波傳播路徑損耗
2.3 ETC系統的電磁波傳播路徑損耗模型
3 實驗研究



4 結 論

