基于有限元分析的間隙檢測線圈間距優化研究*

廖珍貞, 靖永志, 張晨昊, 彭 濤

(1.磁浮技術與磁浮列車教育部重點實驗室,四川 成都 610031； 2.西南交通大學 電氣工程學院,四川 成都 610031)

0 引 言

磁浮列車利用電磁懸浮力使列車懸浮于軌道之上，從根本上解決了輪軌之間的摩擦，在列車運行時只有空氣阻力，因此磁浮列車具有速度快、爬坡能力強和噪音小等優點，具有廣闊的發展前景[1～3]。為了保證列車能正常、穩定地懸浮，懸浮系統擔負著關鍵的核心任務，間隙傳感器為懸浮系統提供電磁鐵與軌道之間的懸浮間隙值。工程上因為軌道熱脹冷縮特性以及道岔等特殊位置的需要，部分相鄰兩段軌道之間設有最大約40 mm的軌道縫隙，當間隙檢測線圈經過軌道縫隙時，測量值會有較大的誤差。為使傳感器經過軌道縫隙時始終能檢測到準確的間隙值，傳感器內至少有2個保持一定間距的檢測線圈。兩個檢測線圈間距越小時線圈之間的耦合越大，并且兩個線圈過縫的誤差也越大；間距越大時，兩個線圈都偏離真實的檢測點，并且會導致傳感器體積增大。以長沙中低速磁浮工程為例，懸浮控制系統要求間隙傳感器過縫時的檢測誤差小于0.5 mm，因此需要對間隙檢測線圈的間距進行優化，得到滿足誤差要求的最小間距值，從而縮小傳感器的體積以達到列車輕量化的目的。

1 間隙傳感器的工作原理

磁浮列車運行時列車和軌道沒有接觸，所以間隙傳感器必須是非接觸式測量，同時列車的運行環境比較復雜，因此中低速磁浮列車懸浮間隙的測量采用電渦流式傳感器。電渦流傳感器原理和等效電路圖如圖1所示，當檢測線圈

流過交變電流I1時，線圈周圍會產生交變的磁場H1，根據法拉第電磁感應定律，金屬導體在交變磁場中會產生渦流，該渦流產生的交變磁場H2與H1方向相反，從而削弱H1的磁場[4,5]。

圖1 電渦流傳感器原理和等效電路圖

圖1中右側為電渦流傳感器的等效電路，R1和L1為檢測線圈的電阻和電感，R2和L2為軌道內電渦流效應的等效電阻和電感，M為L1和L2之間的等效互感[6]。

由基爾霍夫定律，列出回路1和回路2的電壓方程為

計算線圈的等效阻抗為

式中 等效電感Leq為

式中L1為靜磁效應電感，后部分為渦流效應產生的電感，在渦流傳感器中，渦流效應占主導作用。當懸浮間隙較小時，渦流效應較強，渦流效應產生的電感較大，故等效電感Leq較小；當懸浮間隙變大時，渦流效應變弱，等效電感Leq變大，因此，間隙傳感器檢測線圈電感值的大小能夠反映實際間隙值。

2 ANSYS有限元模型的建立

當傳感器位于軌道縫隙時，由于磁場分布較為復雜，檢測線圈的電感以及線圈之間的互感計算較為困難，無法利用電路的等效數學模型對間隙傳感器過縫時的特性進行準確分析。ANSYS是一種常用于電磁場分析的大型有限元計算軟件，該軟件包含不同的子模塊，可分別用于電磁場分析、結構力學分析、流體力學分析、熱分析以及耦合場分析[7,8]。ANSYS有限元分析利用能量法計算電感值，得出的電感只與電磁場的最終分布狀態有關，因此，即使在電磁場分布極其復雜的情況下得出的結果也足夠精確。在進行有限元分析時只需要構建合適的仿真模型，通過選擇子模塊并設置合適的物理參數，就可以得出線圈在不同情況下的電磁參數[9,10]，檢測線圈電感的整體仿真流程如圖2所示。

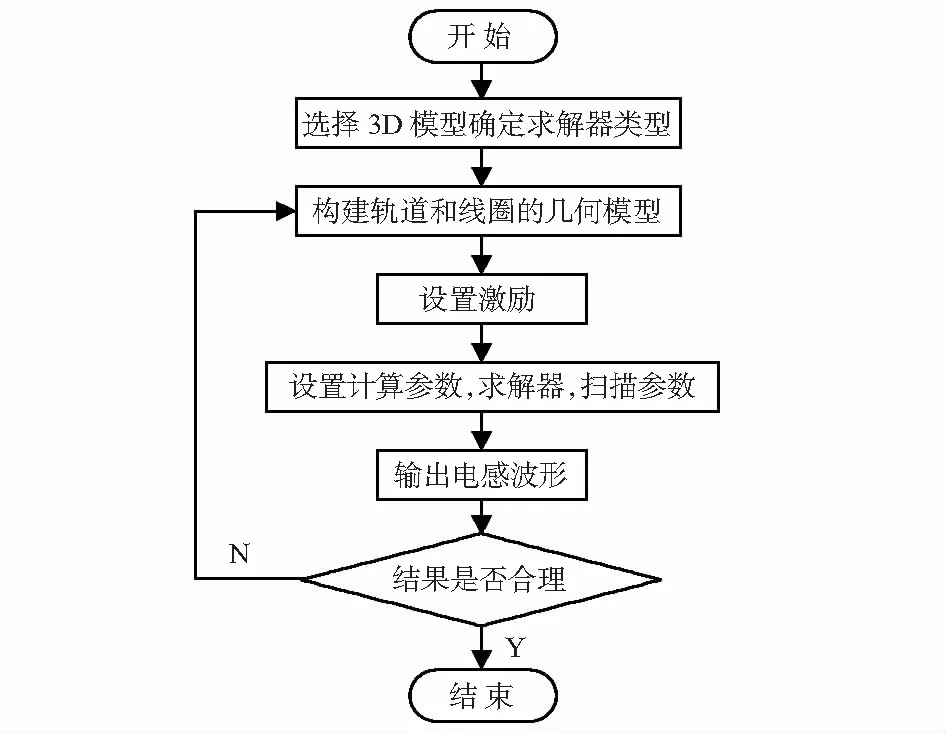
圖2 線圈電感求解流程圖

實際的間隙傳感器因為軌道銜接縫隙的存在，至少包含兩個檢測線圈，當一個線圈過縫時另一個線圈仍能檢測出真實間隙值，因此構建的三維模型中應包括左右側兩段軌道以及兩個保持一定距離的檢測線圈。根據仿真流程，將求解器的類型設定為渦流場，軌道和線圈的材料分別設為A3鋼和銅，線圈半徑為30 mm，具體的線圈過軌道縫隙模型如圖3所示。

圖3 線圈過軌道縫隙的三維模型

在定義完模型材料和激勵源后進行網格剖分，ANSYS只對線圈正下方軌道內部有渦流的區域進行加密剖分，既能保證計算結果的精度又能減少計算量。

3 線圈檢測特性仿真與間距優化

3.1 線圈垂向檢測特性

由間隙傳感器的檢測原理可知，為得到真實的間隙值，需要知道檢測線圈的間隙—電感特性，懸浮間隙傳感器中兩個檢測線圈之間存在互感，線圈間距不同時互感不同導致間隙—電感特性也有所差別。設兩個線圈圓心之間的距離為線圈間距D，分別對線圈間距為70,80,90,100 mm時的垂向特性進行仿真其結果如圖4所示。

圖4 不同線圈間距下的垂向特性曲線

電感值隨著懸浮間隙的變大而變大，間隙較小時靈敏度較大，間隙較大時曲線趨于平緩；同一懸浮高度下，兩個線圈之間的距離變小時，其等效電感值也隨之變小，且電感值的變化與線圈間距的變化為非線性關系。

當列車以額定懸浮間隙8 mm通過軌道縫隙時，懸浮控制系統要求間隙檢測誤差小于0.5 mm，也即是傳感器輸出的值應該在7.5～8.5 mm之間。圖4中的局部放大圖顯示了線圈在懸浮間隙為7.5～8.5 mm時的電感值的范圍， 也就是說線圈在通過軌道縫隙時，電感值不應超出此范圍。

3.2 線圈過軌道縫隙特性

相鄰兩段軌道之間的縫隙一般在10～40 mm范圍內，只要在最大軌道縫隙 40 mm時能夠滿足誤差要求，則必定適用于這一范圍內所有軌道縫隙情況。為了初步確定一個比較合適的線圈間距范圍，在軌道縫隙為40 mm，懸浮高度等于8 mm時，分別設定線圈間距為70,80,90,100 mm進行雙線圈過縫特性仿真，仿真結果如圖5所示。

圖5 不同線圈間距時過縫特性曲線

以軌道縫隙的中點作為仿真模型坐標系中的零點，圖5中橫坐標為兩線圈之間的中點在軌道的位置，起始時線圈的中點在-120 mm處，兩個線圈都在左側軌道上方。當線圈1向右平移時，線圈的電感值逐漸增大，當線圈1的圓心在縫隙中點時，其電感達到最大值，線圈1遠離軌道縫隙時電感值逐漸減小，直到最后線圈1離開軌道縫隙完全進入右側軌道，電感恢復正常值。線圈2平移時的電感變化特性和線圈1一樣，其電感變化曲線關于0點位置左右對稱，兩個線圈曲線波峰之間的距離為線圈間距。

當兩個線圈的中點位于軌縫中點上方時，兩個線圈距軌縫中點距離相等，模型左右兩部分關于軌縫中點對稱，所以線圈1和2的電感值相等，對應特性曲線中橫軸坐標零點上方的交叉點位置。不同線圈間距時交叉點值偏離正常值有所不同，線圈間距越小時交叉點電感值與標準值差異越大。顯然間隙傳感器中電感值較小的線圈檢測結果更接近于真實值，交叉點處兩個線圈電感值相等時誤差最大，因此，為保證線圈過縫時滿足誤差要求，只要控制交叉點的誤差滿足要求即可。依據線圈垂向特性曲線可得到不同線圈間距時交點處對應的檢測誤差如表1所示。

表1 線圈過軌道縫隙時的間隙檢測誤差 mm

由表1可知，過縫時的最大檢測誤差與線圈間距呈反比關系，線圈間距越大誤差越小，并且誤差小于0.5 mm時的最小線圈間距必定在80～90 mm的范圍內。

4 最優線圈間距的確定

為了進一步優化并確定間隙檢測線圈的間距，對線圈間距在80～90 mm范圍內的檢測特性進行細化仿真，不同線圈間距時的過縫檢測誤差分布如圖6所示。

圖6 不同線圈間距下的誤差分布曲線

隨著線圈間距的增加，懸浮間隙誤差減小。線圈間距等于86 mm時，檢測誤差為0.52 mm，大于誤差要求的0.5 mm門限值；線圈間距等于87 mm時，誤差為0.49 mm，小于誤差要求的0.5 mm門限值。因此，選取線圈間距為87 mm時既滿足誤差要求又能盡量地減小間隙傳感器的體積。

5 結束語

針對磁浮列車間隙傳感器通過軌道縫隙時懸浮間隙測量不準確的問題，采用有限元分析方法對傳感器的線圈間距進行優化。利用ANSYS軟件建立雙線圈通過40 mm軌道縫隙的三維仿真模型，進行了垂向檢測特性和額定懸浮間隙下的橫向過縫特性仿真，得到了不同線圈間距時過軌道縫隙的最大檢測誤差，誤差分布曲線表明線圈間距越小，線圈之間的互感影響越大，過軌道縫隙的誤差也越大。依據過縫誤差小于0.5 mm的要求，對線圈間距在80～90 mm內的檢測特性進行進一步優化仿真，仿真結果表明線圈間距為87 mm是滿足誤差要求時的最小線圈間距。