牙輪鉆頭單金屬密封數值模擬與優化

宋保健,鄒 春，孫 凱，明 鑫，任武化

(1.中石化中原石油工程有限公司，河南 濮陽 457001；2.中石化中原油田分公司 濮東采油廠，河南 濮陽 457001；3.中石化中原石油工程有限公司 鉆井一公司，河南 濮陽 457001；4.中石化中原石油工程有限公司 管具公司，河南 濮陽 457001；5.青海油田機械廠，甘肅 敦煌 736202)

牙輪鉆頭是油氣勘探過程中重要的破巖工具，隨著鉆井深度的增加，井底高壓和振動工況使得鉆頭的壽命受到極大的影響，而鉆頭中的動密封可以阻止外部鉆井液侵入軸承內部，從而延長軸承的壽命[1-2]。在鉆進過程下，由于密封腔中的潤滑油不能及時地從地面進行補給，因此鉆頭動密封工況要比常規工業領域的動密封更加惡劣，間接造成牙輪鉆頭的壽命較短。目前鉆頭動密封主要包括金屬型密封和橡膠型密封。金屬密封(如圖1)主要靠兩個金屬環間一層極薄的油膜來保證動密封的正常工作[3-4]，為鉆頭軸承的壽命提供保障。張寶生[5]、張毅[6]結合有限元仿真和正交實驗法對單金屬密封的橡膠支撐環硬度和部分結構參數進行了優化研究，分析結果表明該優化方法可以顯著地降低密封面的接觸壓力。鉆井現場的鉆頭失效情況表明，鉆井液中的微小磨礪很容易侵入到金屬動密封的接觸面，造成潤滑油的大量泄漏，即便是對密封面進行特殊涂層處理，密封面的磨損依然比較嚴重(如圖2)。因此，如何在保證密封泄漏率的情況下盡可能降低密封面的最大接觸壓力是非常重要的，本文對真實工況下的單金屬動密封進行了數值仿真分析，并結合密封泄漏率求解和響應面方法對密封的泄漏率進行優化。

圖1 牙輪鉆頭單金屬密封

圖2 單金屬密封失效

1 單金屬密封有限元分析

1.1 有限元分析

在不考慮密封傾斜的情況下，單金屬密封可以近似認為是軸對稱模型，因此可以將有限元模型簡化為二維軸對稱模型，考慮環空鉆井液壓力和密封內部潤滑油壓力后的有限元模型如圖3所示。根據參考文獻[7]，鉆頭內部潤滑油和外部泥漿之間的壓差約為0.3～0.7 MPa，本文分析中密封內側外壓差為0.3 MPa，加載在密封外側的鉆井液壓力為20 MPa。該工況下的動密封接觸壓力如圖4所示。

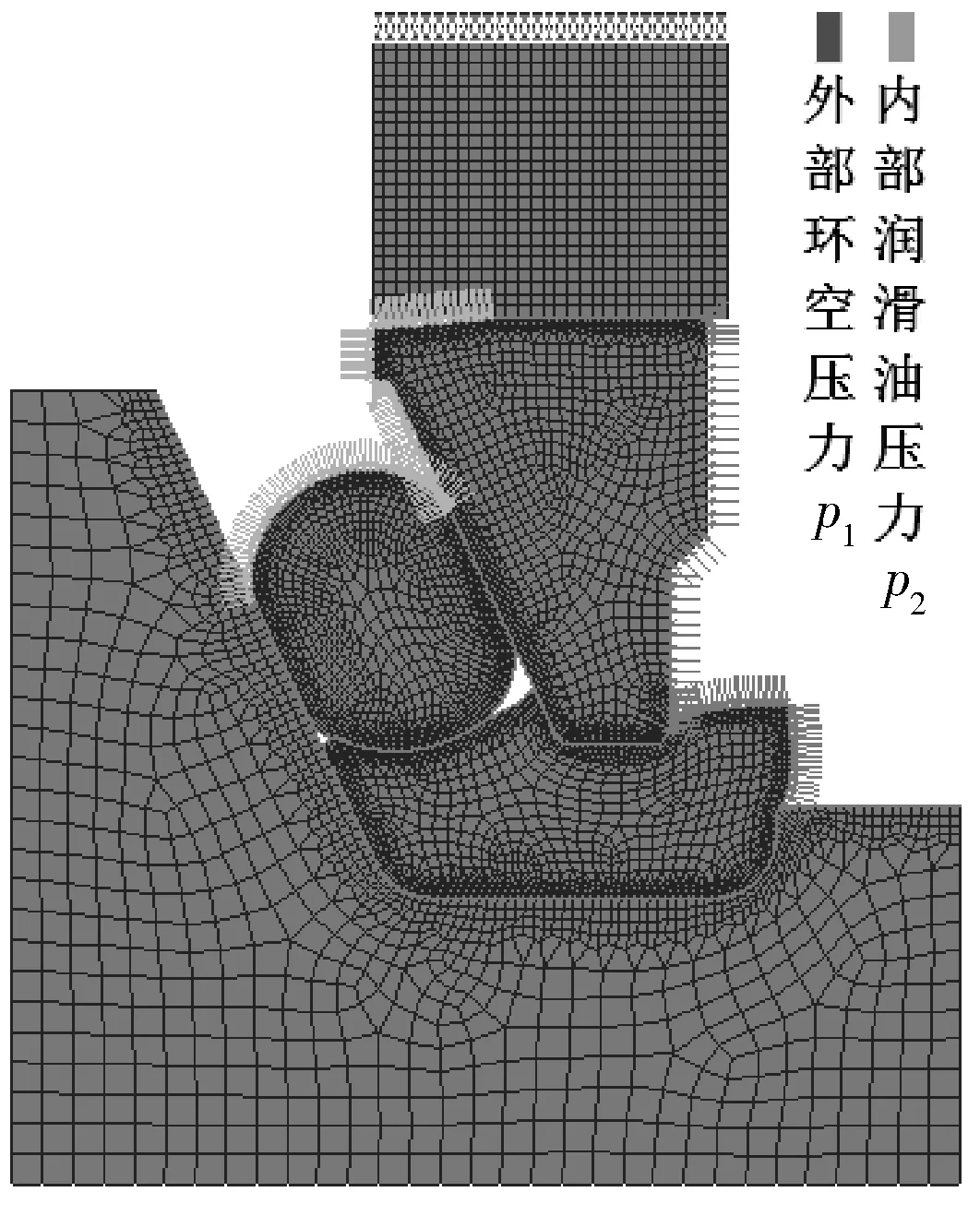
圖3 施加載荷后單金屬密封有限元模型

圖4 高壓工況時單金屬密封接觸應力

根據分析結果可以看出，動密封面的接觸應力從內側到外側逐漸降低。由于高壓環境壓力的作用，接觸應力最大值處于密封面內側的楔入角處，約為66.14 MPa。由于內側接觸應力較大，雖然可以保證動密封面具有較大的接觸比壓，避免了潤滑油泄露，但同時也會造成動密封面間不易于形成穩定的油膜；由于外側接觸壓力較低，鉆井液中的微小顆粒極易進入動密封面，從而使得密封面形成犁狀溝槽。同時，靜環與橡膠O形圈之間的接觸壓力并不高，因此橡膠O形圈易產生相對滑動，造成橡膠O形圈的磨損，降低靜環與O形圈的靜密封性能。由于橡膠支撐環與靜環的倒角處出現了接觸應力集中，當靜環在井底振動作用下發生上下移動時，橡膠支撐環的上部接觸區域將會被壓潰。

1.2 密封泄漏率求解

由文獻[8]可知，通過逆解法對動密封面的油膜厚度進行求解可以提高計算效率，同時還能滿足工程需求。本文對動密封面泄漏率的求解，需要對計算模型進行以下假設：

1) 潤滑油的密度和黏度恒定且為不可壓縮流體。

2) 金屬環表面的粗糙度對動密封面動壓潤滑效應沒有影響。

3) 井底溫度對金屬密封面潤滑狀態無影響。

4) 動密封面的接觸應力分布與密封面之間潤滑油的壓力分布基本一致。

單金屬密封動密封面間的油膜厚度分布可以由Reynolds方程求出，由于不考慮密封面粗糙度的影響，因此二維雷諾方程可以簡化為：

(1)

式中：h為潤滑油油膜厚度；η為潤滑油動力黏度；p為金屬密封面接觸壓力；u為動靜環的相對邊界移動速度。

由于單金屬密封為二維模型，因此可以認為動密封面的油膜厚度在周向上保持一致，則雷諾方程可簡化為：

(2)

根據式(2)確定動密封面的油膜厚度和壓力分布后，金屬動密封的泄露率可以表示為：

(3)

本文在有限元數值模擬的基礎上，先求出動密封面的接觸壓力梯度分布情況，再求出密封面潤滑油膜的分布情況；當接觸壓力梯度達到最大值時，密封面的油膜厚度取最小值hmin，進而求得最小油膜厚度處密封面的泄漏率。

2 動密封泄漏率響應面優化分析

2.1 響應面回歸模型建立

單因素變量分析僅僅改變一個設計變量而得到的優化結果，考慮不全面，有一定的局限性。本文將利用響應面優化方法對單金屬密封進行多因素交互優化。響應面優化方法是通過物理或仿真實驗得到足夠的實驗數據，合理利用試驗設計方法，通過二次回歸方程，擬合出多個變量與響應目標間的函數表達式，采用對回歸方程的分析得到最優響應目標對應的參數組合[9]。根據單金屬密封的設計經驗，本文選用靜環端面的接觸寬度、靜環內側斜面傾角及靜環高度這三個變量作為設計變量，而將動密封的泄漏率作為優化目標，根據試驗原理，采用三因素三水平的響應面模型進行分析[10]，如表1所示。

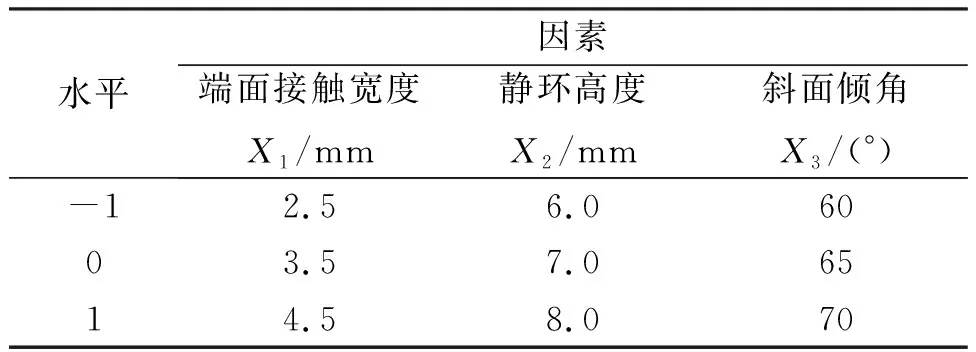
表1 試驗因素與水平

根據正交設計軟件，可以得到17組不同的參數組合。在此基礎上結合有限元仿真分析，得到每組參數組合對應的密封面接觸壓力，再根據密封泄漏率計算方法，得到每組參數對應下的動密封泄漏率。根據Box-Behnken設計方法，采用二次回歸模型擬合17組仿真實驗數據，依據最小二乘法即可求得動密封響應面模型中的回歸系數，密封泄漏率的響應回歸模型方程可以表示為：

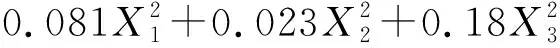
(4)

表2 泄漏量響應面二次模型方差分析

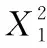
同時，根據計算結果可以得到這三個變量交互作用下對泄漏率的影響，如圖5。由圖5可以看出，隨著密封端面接觸寬度的增大，密封泄漏率也逐漸增大，初期階段靜環高度對泄漏率影響比較小，但當端面接觸寬度大于3.5 mm時，泄漏率隨著靜環高度的增加而減小；隨著接觸寬度的增加，斜面傾角對泄漏率的影響并不明顯，但在不同的靜環高度影響下，斜面傾角對泄漏率的影響要大一些，當斜面傾角和靜環高度均為最小時，泄漏率達到最大值，此時這兩個因素之間的交互作用最為明顯。

圖5 三個變量交互作用對泄漏率的影響

3 結果優化與對比分析

為了得到最小泄漏率對應的最佳組合參數組合，需要求解出泄漏率的二次回歸模型方程。借助罰函數法能將多目標優化問題中的一些優化目標設定一定的允許范圍，將該優化問題簡化成了單目標優化問題，也就是將復雜的優化問題轉化成了多個約束條件下的簡單優化問題。為了避免密封面的磨損失效，根據密封的實際工況和材料許用參數，單金屬密封材料的許用使用psv值為60 MPa·m/s(ps為潤滑油的壓力，v為速度)。根據該許用值，當動密封的轉速為300 r/min，密封面的平均直徑為60 mm時，ps的峰值接觸應力約為67 MPa。根據此條件可以將該優化問題可以轉化為單目標優化問題[11-12]：

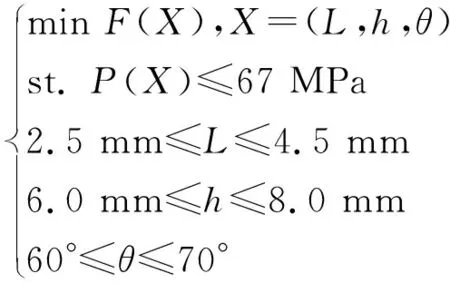
(5)

借助優化軟件Design-Expert 8.0中的優化模塊，優化目標函數F(X)及對應的參數值可以被計算出來。

在該優化方案設定的結構參數變動范圍內，經過17次迭代，能得出17組優化目標值及相應的結構參數組合，然后將期望值最高的密封結構參數模型和初始的密封結構模型分別進行有限元計算，可以得到對應的密封面最大接觸壓力與泄漏率，對比情況如表3所示，可以看出優化后動密封的泄漏率降低了0.104 6 mm3/s，比優化前降低了約35.98%，同時密封面最大接觸壓力也比優化前的模型降低了約15%，可以有效地減緩密封面的磨損，延長密封的壽命，并且優化后的密封面最大接觸壓力也小于材料允許的許用最大接觸壓力。同時也說明了響應面方法在單金屬密封泄漏率和接觸壓力優化中的可行性[12]。

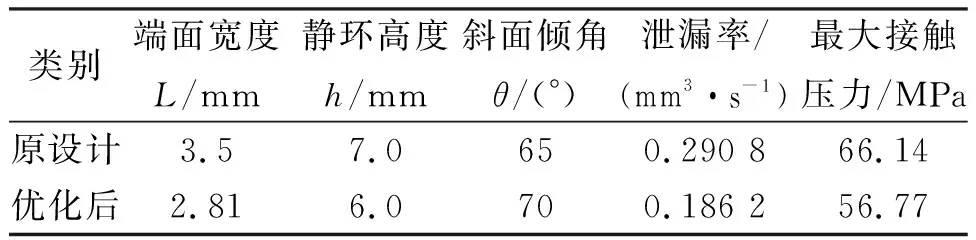
表3 優化前后的結果對比分析

優化后的動密封接觸壓力分布如圖6所示，優化后靜環內側楔入角處的應力集中現象有了明顯改善，最大接觸壓力由初始模型中的66.14 MPa下降至優化后模型的56.77 MPa，有利于密封腔內潤滑脂進入密封面，起到較好的潤滑作用，避免了密封面內側的磨損；同時，可以看出密封端面外側的接觸壓力有所升高，從而使得密封端面接觸壓力分布更加均勻，能夠更好地阻止鉆井泥漿中的微小顆粒進入到密封端面。因此，經過優化單金屬密封的結構參數，能有效地改善密封面的接觸壓力分布，有助于提高密封面的密封性能[12]。

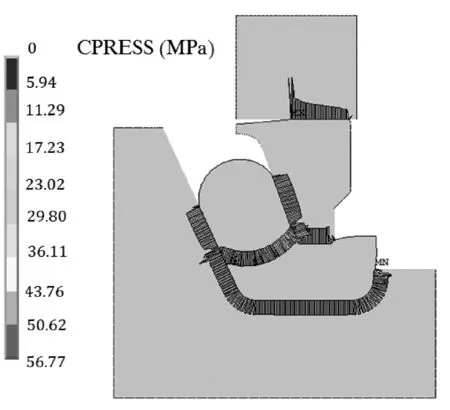
圖6 優化后接觸壓力場分布云圖

4 結論

1) 鉆井工況對牙輪鉆頭單金屬動密封的性能影響比較大，振動環境下密封面容易卡入微小磨礪，造成密封面的損傷，同時橡膠支撐墊也容易發生滑移，鉆頭動密封設計需要綜合評價密封面的磨損和潤滑脂的泄漏。

2) 高壓工況下單金屬密封面的接觸應力呈現從內側到外側逐漸降低的形態，在動密封工作初期時導致密封面內側快速磨損，同時泥漿中的磨礪性顆粒易侵入動密封面，造成潤滑脂的泄露；靜環內側下部倒角處會出現接觸應力集中的現象，易導致橡膠支撐環發生擠壓變形；

3) 響應面法優化分析結果表明，在20 MPa的環境壓力下，優化后單金屬密封的性能可以得到有效改善，密封端面的最大接觸壓力比優化前降低了約15%，密封端面的接觸壓力分布也更為均勻，密封泄漏率比優化前結構降低了約36%，響應面優化法可以有效地解決單金屬密封接觸壓力和泄漏率的多目標優化問題。