側鉆井彎曲段套管抗擠強度研究及應用

牟鵬飛，孟婉濃，劉國祥

(1.東北石油大學 石油工程學院，黑龍江 大慶 163000；2.長城鉆探鉆具公司，遼寧 盤錦 124000)

隨著國內油氣勘探難度逐漸增大，利用側鉆井方式提高老油氣田的采收率將會是今后一段時間油田攻關的重點。在老油氣田改造工程中，側鉆井技術是降本增效的重要技術策略。在側鉆井作業過程中，造斜井段的套管會受到井眼對套管的彎曲載荷作用，導致套管抗擠強度受到影響。國內外學者對彎曲套管抗擠強度研究主要集中在曲率方面[1-3]，而在套管橢圓度方面研究較少。

套管抗擠強度計算普遍采用API BUL 5C3—2008標準[4-6]，但該公式存在一些明顯的不足，也就是沒有考慮彎矩、軸向載荷及套管橢圓度的影響。因此，在考慮側鉆井造斜段套管受到彎曲、軸向載荷等共同作用的條件下，建立了側鉆井造斜段套管的力學模型，并結合ANSYS有限元模擬，研究套管強度隨彎曲率的變化規律，分析彎曲、軸向載荷和徑厚比對造斜段套管抗擠強度的影響，提出了抗擠強度與彎曲率、軸向載荷、徑厚比的關系模型。

1 側鉆井造斜段套管力學模型建立

取側鉆井造斜段部分套管進行分析，研究其受力情況。套管抗擠強度受到的載荷主要有2部分構成，一部分是井眼彎曲給套管施加的彎曲載荷產生的軸向應力；另一部分是套管彎曲段自重作用下產生的軸向載荷。在彎曲載荷和軸向載荷共同作用下，側鉆井造斜段套管受到3種應力，即：彎曲應力、剪切應力、徑向應力和環向應力[7]。套管彎曲變形和受力狀態如圖1所示。圖中：p0為井眼對套管外壁的等效外壓，M為側鉆井造斜段套管所受到的彎矩，Fs為套管所受到的剪力。

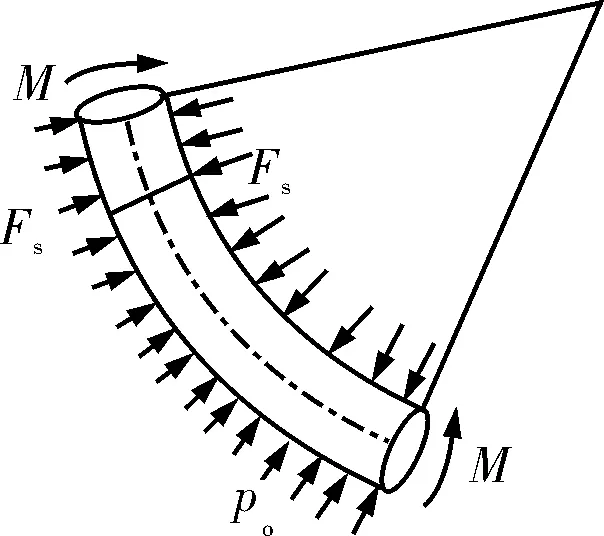
圖1 側鉆井造斜段套管受力模型

將側鉆井造斜段套管簡化為如圖2所示的力學模型，模型一段固定約束，一段施加彎曲載荷F，在外部均勻的施加1 MPa外擠力。套管在受到彎曲載荷作用下，將會發生彎曲和壓扁2種變形，彎曲變形導致套管的軸向應力增大，而壓扁變形會導致套管橫截面的橢圓度增加，從而降低套管的抗擠強度。所以，在計算側鉆井造斜段彎曲受力情況時都必須考慮到以上的這2種情況。

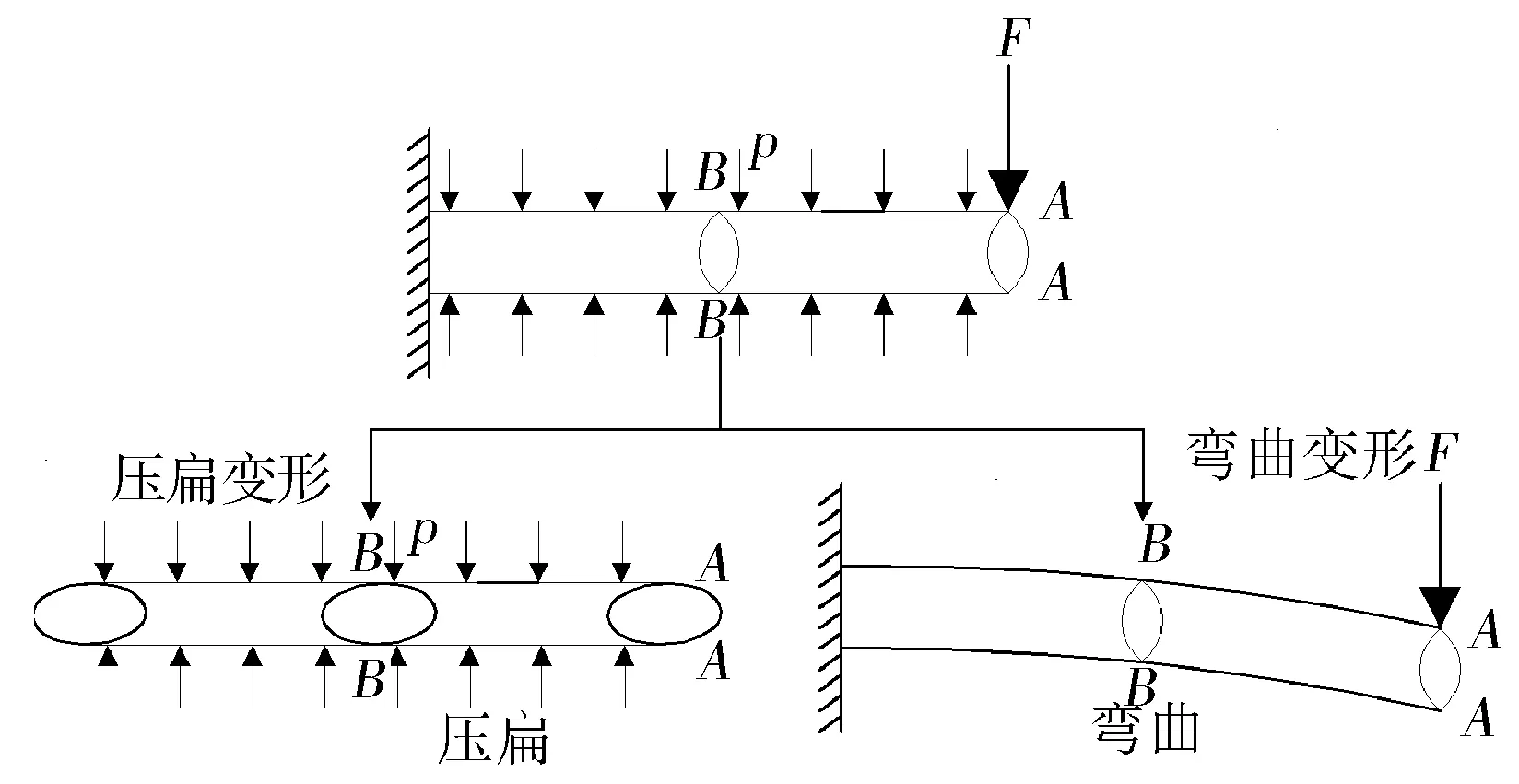
圖2 側鉆井造斜段套管力學模型

通過能量平衡方程式，計算彎曲作用下套管徑向產生的變形為[8]：

(1)

式中：u為套管徑向變形量，mm；t為套管壁厚，mm；D為套管外徑，mm；R為套管彎曲半徑，mm。

2 側鉆井造斜段抗擠強度計算

在未施加彎曲載荷時，套管抗外擠強度為徑厚比相關的函數[9-11]，套管產生的外擠力py為：

(2)

在側鉆井造斜段，套管彎曲受到的載荷主要有2部分構成，一部分是井眼彎曲給套管施加的彎曲載荷，另一部分是套管本身自重產生的軸向載荷。套管在造斜段彎曲狀態相當于在套管的一端施加固定約束，另一端施加載荷，讓套管彎曲。因此，造斜段套管在彎曲模型下，套管中心截面B—B受到彎曲載荷和軸向載荷，使套管在截面B—B受到的等效應力最大，這個橫截面稱為套管的危險截面。

以套管中心截面B—B作為研究對象，由于套管壓扁會導致套管橢圓度增加，從而使套管的抗擠強度降低，同時也考慮到套管彎曲變形的影響，以造斜段套管截面中心A—A為原點建立(p,θ,z)柱坐標。可根據彎矩計算套管彎曲內外側產生的軸向應力為：

(3)

式中：σ′為API最小屈服強度，MPa；θ為計算點的圓心角，rad；E為材料的彈性模量，取206 GPa。

在造斜段套管彎曲自重產生的軸向載荷[12]Fx的計算模型如圖3所示。

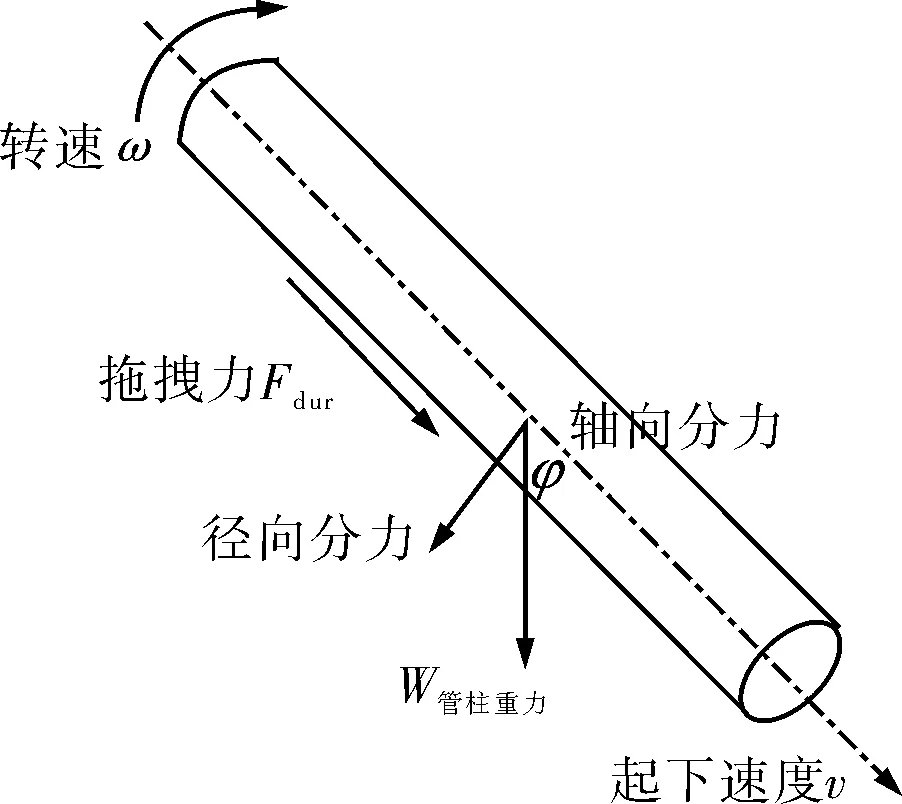
圖3 套管自重產生的軸向應力模型

軸向載荷計算公式為：

Fx=LWacosφ+Fd+Fo+ΔFa-Fb-Ww

(4)

(5)

式中：L為計算點以下套管的長度，m；Wa為套管在空氣中的線重，N/m；φ為計算點處的井斜角，(°)；Fd為套管與井壁摩擦產生的拉力，N；ΔFa為接頭橫截面積變化導致的環空作用在接頭上的力，N，一般取值為0；Fo為套管解卡上提過程中產生的過提力，N；Fb為井底流體作用在套管附件上的力(主要是套管在井眼中受到的浮力)N；Ww為鉆壓，N，一般取值為0；μ為裸眼段摩擦因子；v為上入或下提速度，m/h；w為旋轉速度，r/min，可取0。

根據材料力學理論和拉梅壁厚理論，可以得到彎曲段套管受到的軸向、徑向和環向應力[13]為：

(6)

(7)

(8)

式中：d為套管內徑，mm；p0為套管所受到的軸向載荷，MPa；r為套管壁某個位置到套管中心軸的距離，mm。

套管彎曲使套管在軸向上產生應力，導致彎曲套管內側受壓，外側受拉[14]，其彎曲套管中心截面A—A處的應力分布如圖4所示。

圖4 套管A—A截面的軸向應力分布

由材料力學的理論可知，彎矩在套管截面產生的正應力為[15]：

(9)

在中心截面上集中載荷F產生的剪切應力為：

(10)

式中：M為套管截面處的彎矩，N·m；y為套管截面上某一點到中心軸的距離，m；I為套管截面對中心軸的慣性矩，m4；A為套管中心截面面積，m2。

在套管受到彎矩、剪切和外壓等共同作用下，根據Von Mises屈服失效判別準則，可以得到套管發生屈服失效的等效應力為：

(11)

當彎曲套管的等效應力σM超過套管的屈服強度σy時，最大應力發生在套管內壁上，套管內壁會發生屈服失效。由此可以得到彎曲套管在造斜段彎曲、剪切、擠壓作用下套管的抗擊強度pc為[16]：

(12)

式(10)在推導過程中不但考慮了彎曲對套管截面不圓度的作用，同時也考慮到套管受彎矩和剪切的作用影響，比單一考慮不圓度或彎矩、剪切作用的抗擠強度公式精確，能夠對已有的研究成果做出很好的補充。

(13)

(14)

py=2kyfy(t/D)(1+t/2D)

(15)

(16)

式中：pu為套管的抗擠強度，MPa；pe為彈性擠毀壓力，MPa；py為屈服擠毀壓力，MPa；Hu為衰減因子；ke為彈性擠毀壓力修正系數，取1.089；λ為泊松比，取0.3；ky為屈服擠毀壓力修正系數，取0.991 1；fy為鋼材的屈服強度，MPa；ε為套管橢圓度，%；e為套管壁厚不均度；sr為殘余應力，MPa；hn為應力-應變形狀系數。

3 彎曲套管抗擠強度有限元分析

側鉆井造斜段套管模型所受到的彎矩可以等效為一段固定，一段受到彎曲載荷的受力模型。

(17)

式中：F為施加在套管端面的集中力載荷，N；M為套管在造斜段產生的彎矩，N·m；I為套管的截面慣性矩，m4；L為套管計算長度，m；θ為端面轉角，rad。

利用ANSYS有限元軟件對套管進行模擬計算，計算所需的參數如表1所示。

表1 套管有限元分析計算參數

在ANSYS有限元軟件中，定義單元類型為Solis182，材料類型為各向同性線彈性[19]，分別輸入各尺寸套管的內、外徑，建立套管實體模型，通過正四邊形方式進行網格劃分，每個網格50 mm。在計算中，套管的外擠載荷取1 MPa，均勻的分布在套管的外壁上，方向沿法線方向上向里0°。

利用有限元三維建模軟件ANSYS，建立彎曲套管模型，確定曲率的大小，根據材料力學求得套管端部受到的彎曲載荷的大小，方向為x軸正方向[20]，套管三維有限元模型如圖5所示。

（3）水資源論證企業。引進高素質論證人員，提高論證水平；對于不熟悉地區的論證工作，要提前與該地管理部門、技術資料部門和取水企業進行溝通，及時準確地掌握論證所需的基礎性資料。水資源論證企業要具有社會責任感。論證工作要嚴格依據《水資源論證導則》的相關規定，本著對論證工作負責的態度，在依據當地水資源實際情況下，以業主的利益為主，兼顧其他。

圖5 套管三維有限元模型

通過施加外部載荷進行求解，從而得到彎曲套管等效應力分布云圖，如圖6所示。根據施加給套管的約束和載荷可以計算出套管三維模型在各個位置點的等效應力，并且得到在約束條件和載荷環境下套管的最大等效應力。

圖6 彎曲套管等效應力分布云圖

根據圣維南原理[21]，在選取套管的最大應力時，選取部位應該遠離施加載荷和約束部位的套管位置的節點，在這個節點處讀取套管最大應力值。在線彈性和小變形范圍內，給定套管外徑、壁厚、彈性模量和泊松比以及套管所受到的外壓作用時，套管的最大應力強度和外壓之比是一個無量綱常數。

(18)

根據塑性力學Tresca屈服準則，套管應力強度的表達式為：

σi=max(|σ1-σ2||σ2-σ3||σ3-σ1|)

(19)

當套管中最大應力值達到材料的屈服強度時，此時套管受到的外壓值認為是套管的抗擠強度[22]。套管抗擠強度計算式為[23]：

(20)

式中：σimax為套管最大應力強度，MPa；p為套管受到的外壓，MPa；σs為屈服應力，MPa；pc為套管抗擠強度，MPa。

4 套管抗擠強度的影響

4.1 造斜段套管彎曲率對抗擠強度的影響

通過固定套管的外徑、壁厚、外擠壓力等值，改變套管的彎曲載荷以確定套管的曲率，從而得到外徑為177.8 mm套管在不同壁厚下抗擠強度的理論解和有限元數值模擬解[23]，如表2～3所示。

表2 外徑177.8 mm及厚度13.72 mm套管抗擠強度理論值與有限元值

注：*表示考慮套管橢圓度的理論計算

表3 外徑177.8 mm及厚度12.36 mm套管抗擠強度理論值與有限元值

注：*表示考慮套管橢圓度的理論計算

表2～3表明，在沒有考慮套管由于彎曲載荷產生套管截面橢圓度的條件下，有限元解比理論解小，相對誤差較大；而當考慮套管橢圓度后，有限元解和理論解的相對誤差減少，說明由于套管在受到彎曲載荷作用下，套管產生不圓度對抗擠強度影響較小。所以，在實際生產過程中，可以忽略彎曲作用產生的套管不圓度影響。

根據表2～3中的數據，可以確定側鉆井造斜段套管彎曲曲率與套管強度關系，如圖7所示。

由圖7可知，隨著彎曲率不斷的增大，套管的抗擠強度不斷下降，呈指數下降趨勢；管壁厚比管壁薄的套管的抗擠強度下降快，當彎曲率到達一定程度(120 °/100m)時，套管的抗擠強度相差不大。

圖7 套管抗擠強度與曲率關系

4.2 徑厚比對套管抗擠強度的影響

套管外直徑和壁厚對造斜段套管抗擠強度影響較大，為了能夠更好地分析不同外徑和壁厚對套管抗擠強度的影響，提出徑厚比的概念。徑厚比是指套管外直徑與套管壁厚的比值。

由ANSYS數值模擬出的套管徑厚比與套管抗擠強度的關系如圖8所示。

圖8 不同曲率的套管抗擠強度與徑厚比的關系

由圖8可知，相同曲率下，套管的抗擠強度隨著徑厚比的增加而降低。當徑厚比一定時，曲率越大，套管抗擠強度越小，說明套管的抗擠強度不僅與套管彎曲率有關，也與徑厚比有關，由此可以證明套管的相對壁厚是套管抗擠強度的主要影響因素；隨著曲率的增加，徑厚比與套管抗擠強度變化趨勢變緩，說明當曲率到達一定程度后，徑厚比對抗擠強度的影響減弱，因此徑厚比對抗擠強度的影響不是固定的。

4.3 軸向載荷對套管抗擠強度的影響

通過對側鉆井造斜段套管受力進行分析，用ANSYS有限元軟件模擬計算了考慮軸向載荷條件時不同曲率下的套管抗擠強度，得到套管抗擠強度隨曲率的變化關系，如圖9所示。

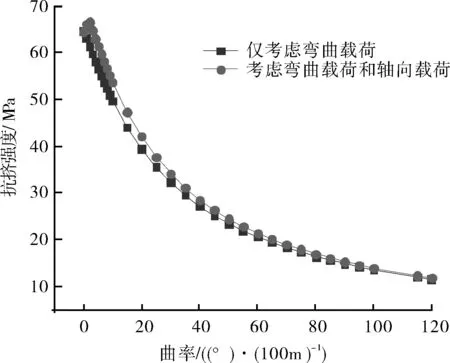
圖9 軸向載荷及彎曲載荷作用下套管抗擠強度與曲率的關系

由圖9(以軸向載荷3 000 N為例)可知，在彎曲條件下，套管抗擠強度僅考慮彎曲載荷和綜合軸向載荷時，下降關系的曲線基本一致，隨著曲率的增大，兩條曲線之間的距離也隨著減少，表明隨著套管彎曲率的增加，軸向載荷對套管抗擠強度的影響在逐漸減少。

根據同一曲率下不同軸向載荷的變化情況，分析軸向載荷對側鉆井造斜段套管抗擠強度的影響規律，如圖10所示。

圖10 套管抗擠強度與軸向載荷的關系

由圖10(以軸向載荷3 000 N、曲率65°/100m的套管為例)可知，造斜段套管的抗擠強度隨軸向載荷的增大而減少，但隨著軸向載荷的增加，抗擠強度下降的速度基本不變。

5 結論

1) 根據拉梅壁厚圓筒理論和Von Mises屈服失效判別準則理論，分析推導出側鉆井造斜段套管在受到軸向載荷、彎曲載荷作用下的抗擠強度計算公式；通過ANSYS有限元軟件分析了曲率、徑厚比、軸向載荷對套管抗擠強度的影響。

2) 隨著彎曲率不斷的增大，套管抗擠強度不斷下降，并且呈指數下降趨勢；管壁厚比管壁薄的套管的抗擠強度下降快，當彎曲率到達一定程度(120°/100m)時，套管的抗擠強度相差不大。

3) 在一定的曲率條件下，套管抗擠強度隨著徑厚比的增加而降低；隨著曲率的增加，徑厚比與套管抗擠強度變化趨勢變緩，徑厚比對抗擠強度的影響不是固定的。

4) 在彎曲條件下，套管抗擠強度僅考慮彎曲載荷和綜合軸向載荷時，隨著套管彎曲率的增加，軸向載荷對套管抗擠強度的影響在逐漸減少。