熱點詞匯的最長時間區間查詢算法

路 暢 何震瀛 荊一楠 王曉陽

1(復旦大學計算機科學技術學院 上海 201203)2(上海市數據科學重點實驗室(復旦大學) 上海 200433)3(上海智能電子與系統研究院 上海 201203)

0 引 言

高效、快速地獲取熱點詞匯在新聞話題追蹤[1]、金融市場分析[2]、商業智能[3]以及社會輿情監測[4]等領域發揮著重要作用。作為話題檢測與追蹤的核心任務之一，熱點詞匯(以下簡稱為熱詞)提取是當前的一個研究熱點。

對語料庫中的關鍵詞及包含關鍵詞的短語、句子進行聚類，是提取熱點話題的一個重要手段。但在實際應用中，為了了解不同約束條件下的熱詞情況，用戶經常查看不同過濾條件下的熱詞，以了解不同時間區域內的熱詞。因此，對關鍵詞提取方法的效率進行優化，能有效提高熱詞檢測的效率。

針對熱詞提取，業界已開展了大量研究工作。Krulwich等[5]利用啟發式規則抽取文檔中重要的詞和短語。Salton[6]提出了TF-IDF算法，刻畫了詞匯對于語料庫或其中一份文檔的重要性。Bun等[7]改進了TF-IDF算法可能將更高的權重賦予語料庫中出現較少的詞匯的不足，提出了TF*PDF算法，將更高的權重賦予出現在多個文檔中的詞匯，以提取整個語料庫的關鍵詞和熱點話題。遲呈英等[8]引入了話題權重，并將其與TF*PDF結合，以更全面地反映話題的熱度分布情況。趙志洲等[9]提出了EHWE算法，對數據進行劃分，在一定程度上優化了TF*PDF的計算過程。但是這些算法的一些共同不足是：

① 僅考慮整個語料庫在某個時間區間關鍵詞，未考慮不同偏好的用戶對不同類別新聞等的查詢需求。

② 面向挖掘任務，時間復雜度較高，當用戶不斷地更改查詢條件(類別和時間區間)時，算法需要對詞頻和包含關鍵詞的文檔數進行重復計算，無法滿足用戶對于關鍵詞提取的在線查詢的需求。

在實際應用中，為了進行新聞追蹤，用戶需要對一組特定的詞匯進行查詢，以尋找這組詞匯能夠成為熱點詞匯所處的最長時間范圍。這要求算法不斷地更新查詢條件，使用TF*PDF算法查詢關鍵詞，以判斷該組特定詞匯是否滿足成為關鍵詞的條件。而由于上述的不足，傳統的TF*PDF算法無法快速、高效地對關鍵詞進行查詢，以滿足用戶在線查詢的需求。

為此，本文對如何有效地使用TF*PDF算法對關鍵詞進行快速提取進行研究。關鍵詞在線提取的兩個核心研究問題是：① 區分不同類別的新聞，以面向不同偏好的用戶；② 在用戶不斷調整查詢新聞的類別、時間區間的條件下，快速、高效地對關鍵詞進行提取。因此，設計在類別、時間兩個維度上對關鍵詞進行在線查詢的方法依然是一個具有挑戰性的問題。針對上述傳統方法的缺點，本文將TF*PDF算法與Prefix Cube結合，優化TF*PDF算法的詞頻統計、包含關鍵詞的文檔數統計的過程，提出一種高效地對二維新聞數據進行關鍵詞提取并查詢最大時間范圍的方法(PCTF)，以根據用戶提供的詞匯，快速尋找這些詞匯能夠成為熱點詞匯的最大區域。

1 相關研究

本文所使用的主要符號如表1所示。

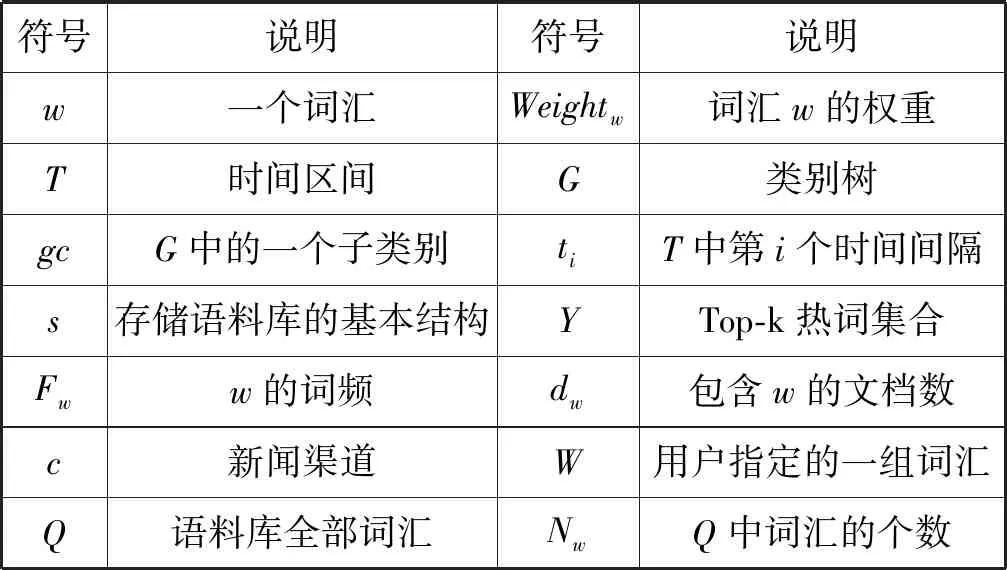
表1 符號說明

1.1 話題檢測與追蹤

話題檢測與追蹤(TDT)的研究始于1996年[10]，旨在從大量的新聞數據流中發現并追蹤新興事件和話題。一個話題由一個種子事件或活動以及與其直接相關的事件或活動組成[11]。熱門話題是指在一段時間內，在某個領域受到人們廣泛關注和討論的話題，同時該話題被多個媒體廣泛報道。熱點話題檢測與追蹤是指發現在一定時期內的熱門話題，并在此基礎上判斷后續新聞報道與該話題的相關性，從而實現追蹤功能。

國內外學者在TDT的基礎上提出了許多熱門話題檢測和追蹤的方法，其中一種流行的方法是基于詞匯權重，檢測文章內容中關鍵或具有代表性的詞匯。常用的方法有Salton等提出的TF-IDF算法[6]，另一個是Bun等提出的TF*PDF算法[7]。與TF-IDF方法相比，TF*PDF算法將更多的權重賦予在整個語料庫中出現頻率較高的詞匯，因此，TF*PDF算法提取的關鍵詞能夠更好地反映話題的熱度，更適用于整個語料庫上的熱點詞匯提取。

1.2 TF*PDF算法

在傳統的TF*PDF算法中，某個詞匯在單個新聞渠道的權重與其在該渠道的詞頻成線性正相關，且與該渠道中包含該詞匯的文檔數成指數正相關。單詞在所有渠道中的權重為其在單個渠道中權重之和，其計算過程如下所示：

(1)

(3)

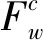
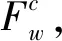
TF*PDF通過計算詞匯的詞頻以及包含該詞匯的文檔數，來尋找大多數渠道中能夠代表熱點話題的關鍵詞。當用戶改變查詢的時間或類別區間時，TF*PDF算法需要遍歷區間內的文檔，來計算詞匯在該區間內的詞頻和包含該詞匯的文檔數，導致了大量的重復計算，使得傳統的TF*PDF算法無法滿足用戶頻繁改變查詢條件的需要。

2 問題定義

本文研究的主要問題為如何根據用戶給定的一組詞匯，快速尋找這組詞匯能夠成為熱點詞匯所處的最長時間區間。

定義1(時間區間T(a,b)) 語料庫的一個時間區間T(a,b)={ta,ta+1,…，tb}，其中ti表示語料庫的第i個時間間隔，也即語料庫中最小的時間單位。特殊地，T(1,Nt)表示語料庫中的整個時間區間，其中Nt表示語料庫中包含的全部時間間隔。

定義2(類別樹G) 語料庫中的新聞具有類別屬性，所有的類別構成了一個樹狀結構G。G中的一個子類別gci={gcx,gcx+1,…,gcy}，其中gcj表示類別gci的第j個子類別。

定義3(類別區間G(x,y)) 類別樹G的所有葉子節點被定義為{g1,g2,…,gNg}，則一個類別區間G(x,y)={gx,gx+1,…,gy}。特殊地，G中的每一個子類別gc都構成一個類別區間。

定義4(詞匯列表L) 語料庫中的一個詞匯列表Lmn={Lwmn}={(w,Fwmn,dwmn)|w同時出現在gm和tn}，其中w是一個詞匯，Fwmn是w在gm和tn中所有文檔的詞頻，dwmn是在gm和tn中包含w的文檔數。

定義5(基本數據結構s) 用于存儲一個語料庫的一個基本數據結構s={Lmn|1≤m≤Ng,1≤n≤Nt}。

定義6(Top-k熱詞Y) 所有語料庫在某個時間區間T(a,b)和一個子類別gc的Top-k熱詞為一個詞匯集合Y={w1,w2,…,wk}，且對于該區間的詞匯w∈Y,w′?Y，有Weightw≥Weightw′。

基于以上的定義，本文研究的主要問題的形式化定義如下：

定義7(熱詞最長時間區間查詢)

給定一組詞匯W={w1,w2,…,wl}，G中的一個子類別gc，查詢初始時間間隔ta，正整數k，尋找一個最長的時間區間T(a,b)，對?w∈W,?i∈(a,b)，在T(a,i)中，有w∈Y。

3 基于改進TF*PDF的熱詞最長區間查詢方法

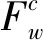
3.1 PC:Prefix Cube

文獻[12]使用Prefix Sum技術提出了一個名為Prefix Cube(PC)的存儲結構。給定存儲一個語料庫的基本數據結構s，首先計算其中一個詞匯w詞頻Fw的Prefix Cube表示為:

(4)

對于一個時間區間T(a,b)和一個子類別gc=G(x,y)，w在這個區間內的詞頻Fw可以通過FPC快速計算：

FPCw(y,b)-FPCw(y,a-1)-

FPCw(x-1,b)+FPCw(x-1,b-1)

(5)

式(5)表明，Fw在區間T(a,b)和子類別gc=G(x,y)構成的二維區間內的詞頻可以通過該二維區間頂點的FPCw來快速計算，從而避免了對該二維區間內的全部文檔進行迭代計算。

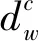
DPCw和FPCw同樣具有式(5)所示的性質，在區間T(a,b)和子類別gc=G(x,y)構成的二維區間，有:

DPCw(x-1,b)+DPCw(x-1,b-1)

(7)

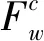
當x=y=m，a=b=n時，式(5)和式(7)可變化為：

Fw=FPCw(m,n)-FPCw(m,n-1)-

FPCw(m-1,n)+FPCw(m-1,n-1)=Fwmn

(8)

dw=DPCw(m,n)-DPCw(m,n-1)-

DPCw(m-1,n)+DPCw(m-1,n-1)=dwmn

(9)

因此，可以通過迭代的方式來計算FPCw和DPCw：

FPCw(m,n)=FPCw(m,n-1)+FPCw(m-1,n)-

FPCw(m-1,n-1)+Fwmn

(10)

DPCw(m,n)=DPCw(m,n-1)+DPCw(m-1,n)-

DPCw(m-1,n-1)+dwmn

(11)

式中：FPCw(1,1)=Fw11,DPCw(1,1)=dw11。因此FPCw和DPCw可以通過迭代的方式進行構建，而不需使用式(4)和式(6)對已經計算出的所有元素進行循環計算。接下來，將FPCw和DPCw合并，以構建出w的Prefix Cube：PCw。最后對所有的單詞進行迭代計算，以構建出整個語料庫存儲s的Prefix Cube：PC。

對PC的構建算法的詳細描述如算法1所示。

算法1構建PC

ConstructPC(s,Nt,Ng,Q)

輸入：語料庫的基本存儲結構s，時間間隔個數Nt，類別樹的所有葉子節點個數Ng，全部詞匯Q

輸出：所有單詞的Prefix Cube：PC

1:Forw∈QBegin

2: FetchFw11,dw11froms;

3: FPCw(1,1)=Fw11,DPCw(1,1)=dw11;

4:Form∈(1,Ng)Begin

5:Forn∈(1,Nt)Begin

6:FetchFwmn,dwmnfroms;

7:FPCw(m,n)=FPCw(m,n-1)+FPCw(m-1,n)-

FPCw(m-1,n-1)+Fwmn;

8:DPCw(m,n)=DPCw(m,n-1)+DPCw(m-1,n)-

DPCw(m-1,n-1)+dwmn;

9:PCw(m,n)=(w,FPCw(m,n-1),DPCw(m,n-1));

10:End

11:End

12:End

13:PC={PCw};

14:ReturnPC;

在算法1中，構建PC需要對語料庫中的全部詞匯、時間間隔和類別樹的葉子節點做循環，因此，算法的時間復雜度為O(NwNgNt)。對于構建出的PC，由于每個PCw的每個元素需要存儲w、FPCw(m,n)和DPCw(m,n)，每個PCw的空間復雜度為O(3NtNg)。因此，整個PC的空間復雜度為O(3NwNtNg)，和原始的s的空間復雜度相同。因此使用PC作為語料庫輔助存儲并不增加存儲的空間復雜度。

3.2 最長時間區間查詢

根據第2節的問題定義，本文所涉及的查詢為用戶給定一組單詞、初始時間間隔、類別和k，查詢該組單詞在該類別上滿足成為熱詞的最長時間區間。這就要求算法不斷地更新時間區間，計算出詞匯的權重，以判斷詞匯是否是Top-k的熱詞。

當使用傳統的TF*PDF算法時，時間區間需要不斷地被更新來計算詞匯權重以查找Top-k的熱詞，TF*PDF算法中的詞頻和包含詞匯的文檔數需要進行大量的重復計算。而當使用PC作為存儲結構時，由于詞頻和文章數可以通過式(5)和式(7)直接得出，這些計算可以被避免。

當用戶給定一組詞匯W={w1,w2,…,wl}、初始時間間隔ta、類別gc和k，查詢該組單詞在該類別上滿足成為熱詞的最長時間區間時，我們以ta為初始點，對ta后的時間間隔進行遍歷以查詢熱詞，并判斷W是否在Top-k熱詞Y中，如算法2所示。

算法2PCTF：查詢最長時間區間

PCTF(W,ta,gc,k,PC,Q)

輸入：詞匯W={w1,w2,…,wl}，初始時間間隔ta，類別gc，整數k，所有語料庫的Prefix CubePC={PC1,PC2,…,PCNc}，全部詞匯Q

輸出：時間區間T(a,b)

1:b=a;

2:{gx,gx+1,…,gy}=gc;

3:Do

4:Weight=?;

5:D=?;

6:b=b+1;

7:Forc∈(1,Nc)Begin

9:lc=0;

Forw∈QBegin

12:End

13:End

14:Forw∈QBegin

15:Weightw=0;

16:Forc∈(1,Nc)Begin

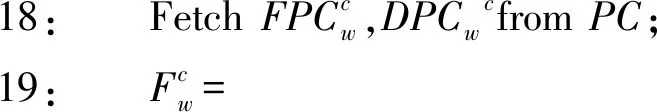
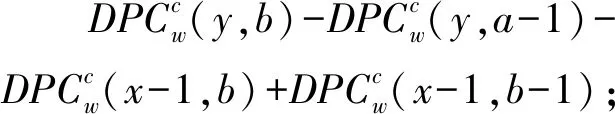
22:End

23:Weight=Weight∪Weightw;

24:End

25:Y=Top-k(Weight);

26:WhileW?Y;

27:ReturnT(a,b-1);

算法2首先獲取給定類別gc的類別區間(x,y)，在7～13行，該算法計算在每個Channel中的詞頻的平方和，時間復雜度為O(NcNw)。隨后算法2依次迭代更新時間區間的終止時間間隔tb，并使用Prefix Cube查詢T(a,b)上所有單詞的權重，時間復雜度同樣為O(NcNw)。最后算法計算Top-k的熱詞，直到用戶給定的詞匯W不滿足熱詞的條件，算法返回時間區間T(a,b-1)。在計算Top-k熱詞時，使用最小堆技術，時間復雜度為O(Nwklogk)，而判斷W?Y需要O(k)的時復雜度，因此，算法的總復雜度為(b-a)O(Nwklogk+2NcNw)。

4 實 驗

本節設計了一系列實驗來比較PCTF算法和傳統的TF*PDF算法在提取熱詞并查詢熱詞所在的最長時間區間的運行效率。

4.1 語料庫

為測試PCTF算法的效率，本文從一些著名的新聞網站——路透社(https://uk.reuters.com)，紐約時報(https://www.nytimes.com)和BBC(https://www.bbc.com)上收集了自2016年1月1日至2017年1月1日的新聞文章。表2列出了三個語料庫的詳細信息。

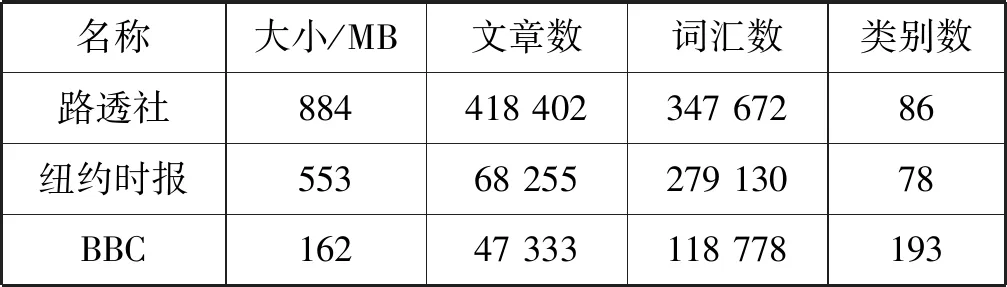
表2 語料庫詳細信息

實驗中，渠道總數Nc=3，語料庫的最小時間單位為天。本文使用了Stanford CoreNLP對語料庫進行了預處理，包括去除停止詞、分詞和詞形還原等。

4.2 實驗環境

采用的實驗環境為：Intel?Xeon(R) CPU E5-2650v3 @ 2.30 GHz×40，128 GB內存和256 GB SSD磁盤，操作系統為Ubuntu Kylin 16.04，程序語言為Java (Version 1.8.0_92)。

4.3 尋找最長時間區間

(1) 改變k通過改變k，研究不同的k對PCTF算法查詢熱詞所滿足的最長時間區間的時間開銷的影響。在本次實驗中，設置初試時間間隔為2016年6月15日(ta=288)，類別為politics(gc=politics，類別區間長度為23)，用戶給定的一組詞匯W={Trump,Clinton,Obama,President}。實驗結果如圖1所示。

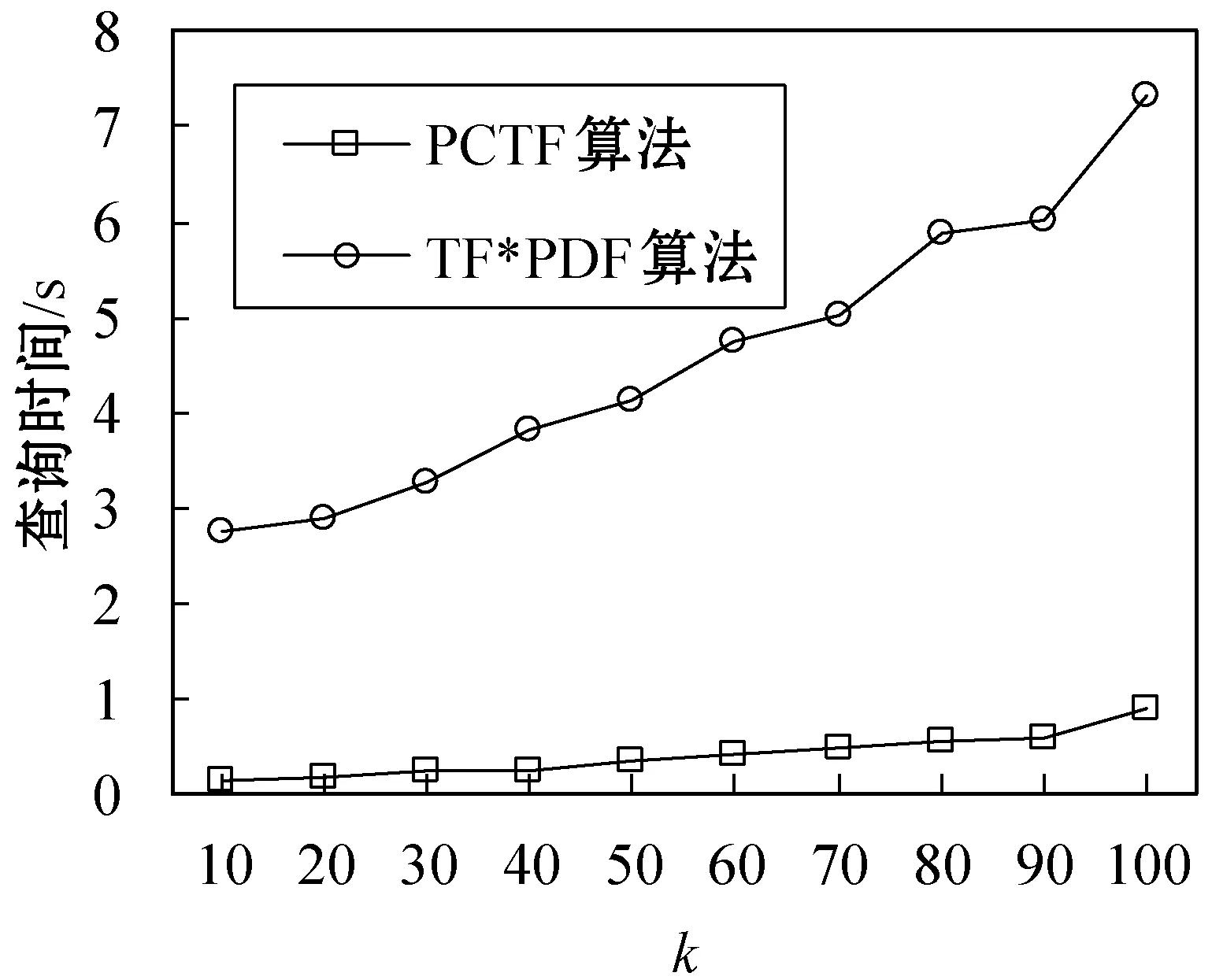
圖1 改變k時查詢時間的變化曲線

從圖 1可以看出，隨著k的增加，PCTF算法和傳統的TF*PDF算法查詢最大時間區間所消耗的時間均有所增加，這是因為在計算出所有詞匯的權重之后，算法需要計算Top-k的熱詞。此外，隨著k的增加，用戶給定詞匯滿足Top-k的最長時間區間的范圍也可能增加。因此，兩個算法的整體時間消耗均有所增加。然而，隨著k的增加，PCTF算法的時間開銷均遠小于TF*PDF算法。

(2) 改變類別和用戶指定的詞匯 通過改變類別和用戶指定的關鍵詞，研究PCTF算法對于不同用戶偏好的適用性。實驗設置初始時間間隔為2016年8月1日(ta=213)，k=50，類別和詞匯分別為：

①gc=basketball，類別區間長度為5，W={NBA,Rockets,Harden}；

②gc=football，類別區間長度為8，W={Spain,Argentina,Ronaldo,Messi}；

③gc=tennis，類別區間長度為3，W={Nadal,Federer,Final}。

實驗結果如圖2所示。

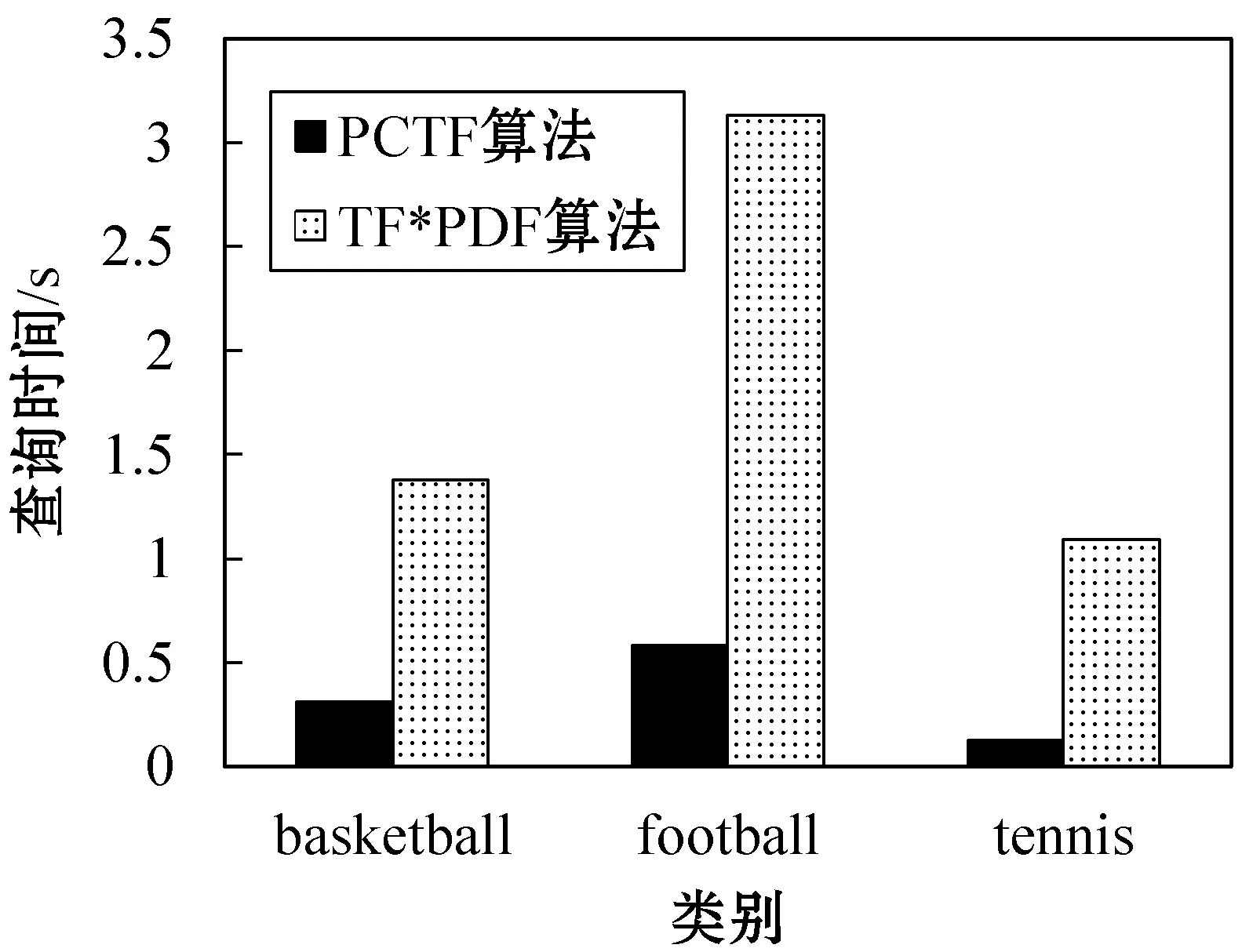
圖2 改變類別和關鍵詞時查詢時間變化的柱狀圖

由圖 2可以看出，對于不同的類別和用戶指定的詞匯，兩種算法在較大的類別區間上有較高的查詢時間。而與TF*PDF算法相比，PCTF算法均能以較低的查詢時間得到最大的時間區間。

(3) 改變初始時間間隔 由于一組詞匯可以在不同的時間區間內都成為熱詞，也即該組詞匯描述的事件發生了多次，可以通過改變初始時間間隔來更加全面地尋找詞匯能夠成為熱詞的最長時間區間。

實驗設置類別為Sports(gc=Sports，類別區間長度為14)，W={NBA,Rockets,Lakers}，k=50，初始時間間隔分別為2016年1月18日(ta=17)，2016年4月11日(ta=101)，2016年10月27日(ta=300)，2016年12月8日(ta=342)。實驗結果如圖3所示。

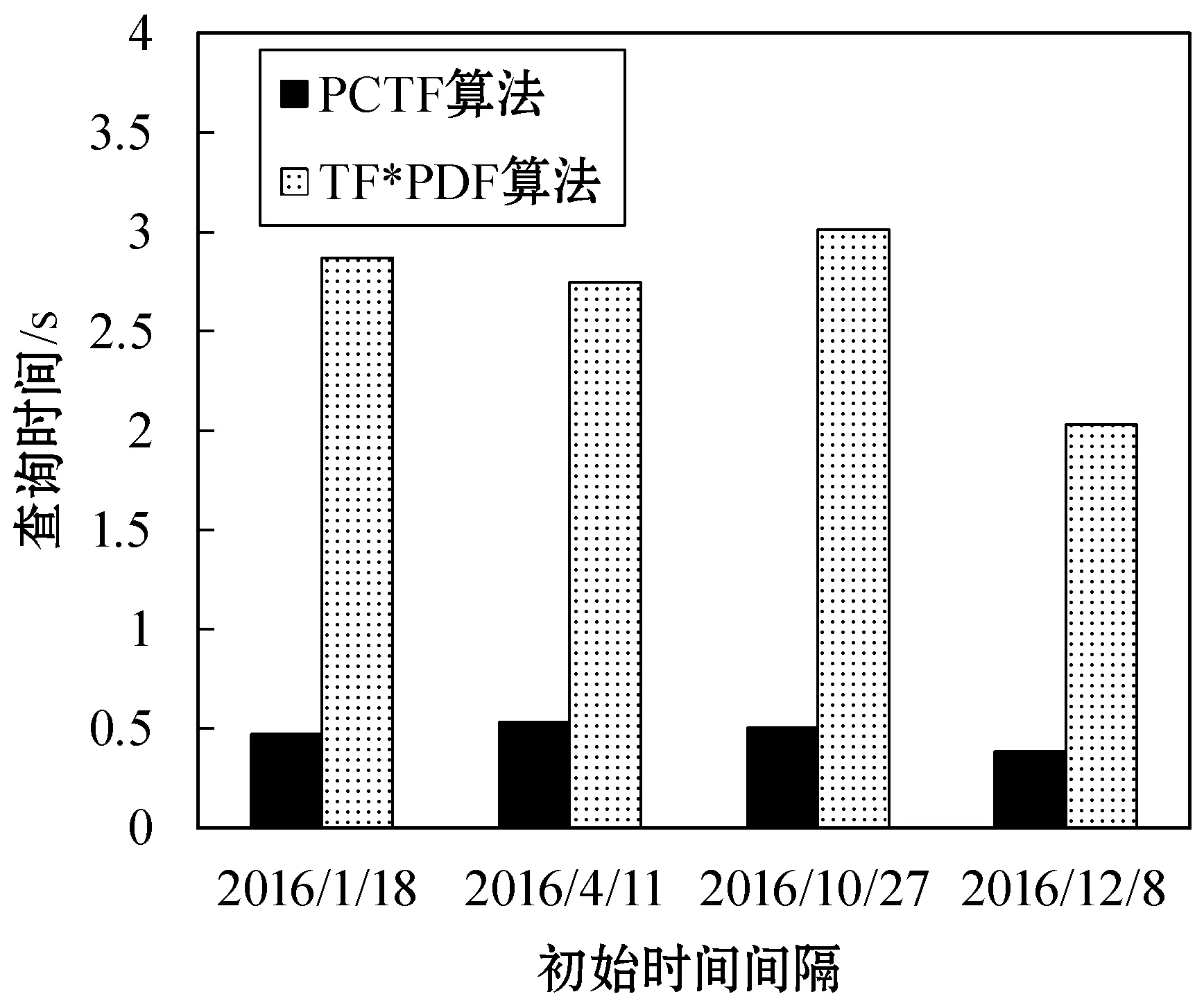
圖3 改變初始時間間隔時查詢時間變化的柱狀圖

由圖3可以看出，當改變查詢的初始時間間隔時，PCTF算法均能保持較低的查詢時間復雜度，且查詢時間較為穩定。

通過以上的實驗我們可以看出，PCTF算法能夠較好地應對不同的查詢場景。當用戶不斷改變k、查詢類別和詞匯以及查詢的初始時間間隔時，傳統的TF*PDF算法耗時較長，而PCTF算法均能以小于1 s的時間消耗查詢出用戶給定詞匯的最長時間區間。因此PCTF算法能夠面向不同的用戶，快速高效地對關鍵詞進行提取，并查詢詞匯所在的最長時間區間。

5 結 語

本文對二維區間內關鍵詞提取的在線算法進行研究。基于Prefix Cube，對傳統的TF*PDF算法進行改進，提出了FPC、DPC的存儲結構，快速、高效地對關鍵詞進行提取，并能快速查詢用戶指定的詞匯成為關鍵詞的最長時間區間。PCTF算法在空間復雜度不變的情況下，降低了關鍵詞提取的時間復雜度，具有能夠面向不同偏好的用戶和較好地應對用戶不斷更新查詢條件的優點。試驗結果表明，PCTF算法在不同查詢條件下，查詢所用時間優于傳統的TF*PDF算法。在自然語言處理方面，由于本文的算法采用Stanford CoreNLP對新聞文章進行分詞，算法對中文文檔的支持性不足。在未來的研究中，將考慮數據的更新及更加復雜的查詢，此外，將考慮使用更多中文分詞庫以增加算法對中文文檔的支持能力。