基坑放坡開挖對下方既有地鐵隧道影響計算及風險預測*

卜康正，鄭先昌，沈 翔，劉繼強，張萬照

(1. 廣州大學 土木工程學院，廣東 廣州 510006； 2. 中鐵南方投資集團有限公司，廣東 深圳 518052)

0 引言

隨著城市快速發展，地下工程建設項目數量以及規模日益增大，在已建地鐵隧道上方的基坑工程也越來越多。基坑開挖會引起下方既有地鐵隧道隆起變形，隆起變形過大則會破壞隧道結構，甚至致使隧道管片破裂，管片接縫處出現漏水、漏泥現象[1-2]。為了確保已建地鐵隧道的結構安全，深圳市《城市軌道交通安全保護區施工管理辦法(暫行)》中，對鄰近既有地鐵隧道施工對其影響的量化指標行為做以下規定[3]：1)既有隧道結構絕對沉降量及水平位移量≤20 mm(包括各種加載和卸載的最終位移量)；2)既有隧道的相對變形曲率≤1/2 500(在既有地鐵區間隧道上方實施大面積的加卸載工程中，該指標是極其關鍵的一個指導性技術指標)；3)由于建筑物垂直荷載(包括基礎地下室)及降水、注漿等施工因素而引起的既有隧道附加荷載≤20 kPa。因此，研究基坑開挖對下方既有地鐵隧道影響這一問題具有重要意義。

目前，學者主要通過數值模擬[4-6]和理論計算[7-9]2種方法研究基坑開挖對下方既有地鐵隧道影響。其中，理論計算研究結果與實測值吻合良好，且相比于數值模擬研究，不需進行復雜的三維數值建模，因此更加簡便。鑒于此，越來越多學者利用理論計算方法分析基坑開挖對下方既有地鐵隧道影響[7-9]，即基于Mindlin應力解，推導得到矩形基坑開挖引起下方既有地鐵隧道的附加荷載，并通過兩階段分析方法計算得到隧道位移和相對變形曲率。但在實際工程中，對于淺基坑因放坡開挖的經濟適用性而常被采用，可目前尚未有學者針對放坡開挖基坑對下方既有地鐵隧道影響提出有效的理論計算方法。

此外，由于土層參數的不確定性，隧道結構的安全風險尚需運用科學的方法預測。針對這一問題，徐耀德等[10]利用層次分析、模糊綜合評價等方法，建立基坑工程與隧道各項因素下的風險判別矩陣，預測隧道結構的安全風險；陳大川等[11]通過熵權法完善風險判別矩陣各項因素的權重確定過程，使風險預測方法更加合理。但前人研究大多只能分析得到隧道最有可能發生某一等級的風險，未能計算得到隧道結構處于各級風險的概率，不利于工程人員根據隧道結構處于各級風險的大小制定完備的風險預防方案。因此，現有研究尚有不足，還需做進一步研究。

本文基于Mindlin應力解[12]，推導得到放坡開挖基坑引起下方既有地鐵隧道的豎向和橫向附加荷載，通過兩階段分析方法[7]，計算得到地鐵隧道的豎向和橫向位移，并基于正態分布概率模型對土層物理力學參數隨機取值，利用蒙特卡羅方法對地鐵隧道結構處于各級風險的概率進行計算，以期為基坑下方既有地鐵隧道結構的安全評估提供參考。

1 基坑開挖引起隧道的豎向附加應力公式

設基坑坑頂的縱向邊長為a，橫向邊長為b，深度為h，隧道埋深為z0，基坑與隧道位置關系如圖1所示。

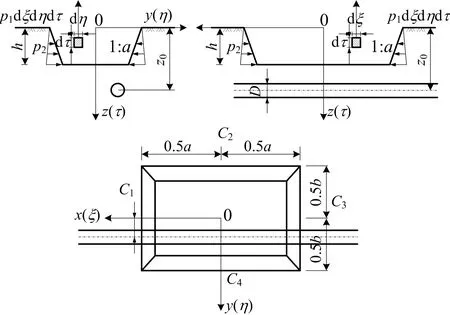
圖1 基坑與隧道位置關系Fig.1 Position relationship of foundation pit and tunnel

由文獻[13]可知，基坑開挖卸荷時，坑內土體存在殘余應力，則坑內每一點土體豎向卸荷為p1=γ(1-λ)，利用Mindlin應力解，通過積分得到坑內全部土體豎向卸荷引起下方既有隧道軸線上的點(x,y0,z0)豎向附加應力為：

(1)

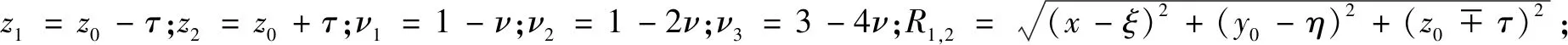
基坑開挖卸荷時，在基坑側壁Cn(n=1,2,3,4)面產生水平三角形荷載p2=K0γτ，則p2引起隧道軸線上的點(x,y0,z0)豎向附加應力為：

(2)

式中：z3=z0-τ；z4=z0+τ；βn=(η,ξ,η,ξ)；Xn=(x-0.5a+ατ,y0+0.5b-ατ,x+0.5a+ατ,y0-0.5b-ατ)；

K0為坑壁外土的側向土壓力系數。

所以在坑內土體豎向卸荷和坑壁水平荷載的作用下，既有隧道軸線上任意一點(x,y0,z0)的豎向附加應力為：

(3)

利用高斯積分法求解σz中的定積分項，乘以隧道直徑D，得到隧道軸線上各點的總豎向附加荷載集合Qz。通過兩階段分析方法[7]，并運用matlab編程計算得到隧道軸線上各點的豎向位移和相對變形曲率集合Uz。

2 基坑開挖引起隧道的橫向附加應力公式

坑內全部土體豎向卸荷引起隧道軸線上點(x,y0,z0)的橫向附加應力為：

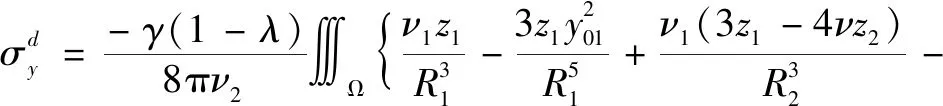
(4)

式中：y01=y0-η。

基坑側壁C1、C3面水平三角形荷載引起隧道上點(x,y0,z0)的橫向附加應力為：

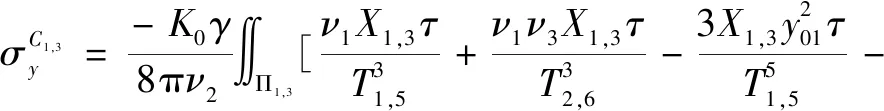
(5)

式中：X1,3=±x-0.5a+ατ。

基坑側壁C2，C4面水平三角形荷載引起隧道上點(x,y0,z0)的橫向附加應力為：

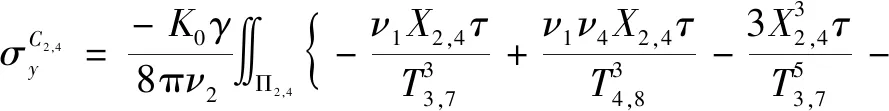
(6)

式中：X2,4=y0±(0.5b-ατ)；ν4=5-4ν；ν5=3-2ν。

所以在坑內土體豎向卸荷和坑壁水平荷載的作用下，地鐵隧道軸線上任意一點(x,y0,z0)產生的橫向附加應力為：

(7)

通過第1節的方法，得到隧道軸線上各點的總橫向附加荷載集合Qy、以及橫向位移和相對變形曲率集合Uy。

3 算例對比驗證

算例一：上海市某基坑工程[7,11]，坑頂縱向邊長a為240 m，橫向邊長b為230 m，開挖平均深度h約為7 m，基坑放坡坡度α為0。地鐵1號線隧道位于基坑斜下方，上、下行線均平行于基坑縱向側邊，埋深均為14.9 m。隧道直徑D均為6.2 m。其中，下行線隧道軸線在基坑側邊以外6.5 m處，上行線隧道軸線在基坑側邊以外20.5 m處，縱向抗彎剛度EI為1.26×108kN·m2。各土層物理力學參數取值可參考文獻[7,14]。兩階段分析方法求解所需要的隧道所在土層豎向基床系數kz可根據Vesic公式[15]計算，即：

(8)

式中：Es為土的壓縮模量。

兩階段分析方法求解所需要的隧道所在土層橫向基床系數ky可根據式(9)[16]求得：

ky=φ·Es

(9)

式中：φ為橫向基床系數的比例系數，可根據文獻[17]中得到。

本算例豎向基床系數kz的計算結果為4.18×103kN/m2，橫向基床系數ky的計算結果為6.0×103kN/m2。

將本文理論計算結果與實測值、文獻[7]方法的理論計算結果進行對比，結果如圖2所示，豎向位移以隧道隆起為正，橫向位移以隧道向基坑內側移動為正，下同。由于文獻[7]未提出橫向位移的計算方法，且文獻[14]未給出上行線橫向位移實測數據，因此本文只將下行線橫向位移計算結果與實測數據作對比。

圖2 計算結果對比Fig.2 Comparison of calculation results

由圖2(a)可知，相比于文獻[7]對下行線隧道豎向位移的理論計算結果，本文的理論計算結果與實測數據更為吻合，原因是本文計算坑內土體豎向卸荷引起隧道的附加荷載時，考慮到坑內土體是被多次分小塊開挖完的，豎向卸荷的作用位置應在坑內土體原位置。而文獻[7]卻假設坑內全部土體被一次性開挖完，未作任何等效的情況下直接將豎向卸荷的作用位置移動至坑底，這與實際情況不符。因此，本文對下行線隧道豎向位移的理論計算方法更加符合實際工程；由圖2(b)可知，本文的下行線隧道橫向位移理論計算結果略大于實測數據，計算結果偏于安全，總體上可用于隧道的安全評估；由圖2(c)可知，上行線隧道豎向位移實測數據波動較大，且本文和文獻[7]的理論計算結果曲線雖與實測數據曲線總體趨勢相同，但數值吻合度不高，原因是上行線隧道位于上海市共和新路與共和新路高架橋正下方，極易受到地面行車荷載和小范圍道路改造工程的影響，而且鄰近基坑開挖引起上行線隧道豎向位移數值較小，造成上行線隧道豎向位移數值在鄰近基坑開挖、地面行車荷載和小范圍道路改造工程3者共同影響下出現較大波動的情況。同時表明本文理論計算方法仍存在一定的局限性，不可用于道路正下方的隧道。

4 風險預測

在實際工程中，各土層物理力學參數并非如算例一[7]中的定量，而是在一定數值范圍內的隨機變量，因此，有必要根據土層物理力學參數的不確定性預測隧道結構處于各級風險的概率：根據隧道結構安全物理表現因子的量化指標的預警值、報警值、控制值對風險進行分級，計算各級風險發生的概率。

4.1 風險分級

根據《城市軌道交通地下工程建設風險管理規范》[18]第4.3節，隧道結構安全的風險可分為4個等級，本文選取隧道豎向和橫向附加荷載、位移以及相對變形曲率共2類、6個隧道結構安全物理表現因子的量化指標的預警值(0.6倍控制值)、報警值(0.8倍控制值)、控制值作為分界點，具體取值如表1所示。由于本文研究的隧道附加荷載為沿隧道縱向的線荷載，因此還需乘以隧道直徑D(下面算例二中D=6 m)，才能得到隧道附加荷載的各個分界值。

4.2 各級風險發生的概率計算

各土層物理力學參數包括基坑內土層的重度γ、泊松比ν1、靜止土壓力系數K0和隧道所在土層泊松比ν2、壓縮模量Es，可在一定數值范圍內的隨機取值，且各取值出現的概率呈正態分布[21]。鑒于此，本文通過各土層物理力學參數對6個因子的敏感性分析，選取其中較為敏感的l個參數并對其取值進行隨機抽樣，利用蒙特卡羅方法[22]得到各級風險發生的概率。蒙特卡羅方法計算概率的步驟：

1)由于每個土層物理力學參數都服從正態分布概率模型，因此采用matlab編程，每次在l個較為敏感的土層物理力學參數取值范圍內隨機產生l個數值，組成1組數據。進行m次隨機抽取試驗則有m組數據。

2)將每組數據代入各計算公式，取每組計算結果中隧道豎向和橫向最大附加荷載、最大位移以及最大相對變形曲率共6個因子的最大值。

3)根據表1中6個因子量化指標的風險等級劃分標準，對各組所取6個因子最大值的計算結果進行統計歸類，得到6個因子各級風險的發生概率。

4.3 算例分析

算例二：深圳市某待開挖基坑工程，坑頂縱向邊長a為111.6 m，橫向邊長b為66.2 m，開挖深度h為10 m，基坑放坡坡度α為1.5。地鐵11號線下行線隧道位于基坑下方，隧道軸線在距離基坑中軸線8.5 m處，且平行于基坑中軸線。隧道埋深為15.75 m，直徑D為6 m，縱向抗彎剛度EI為3.55×107kN·m2。

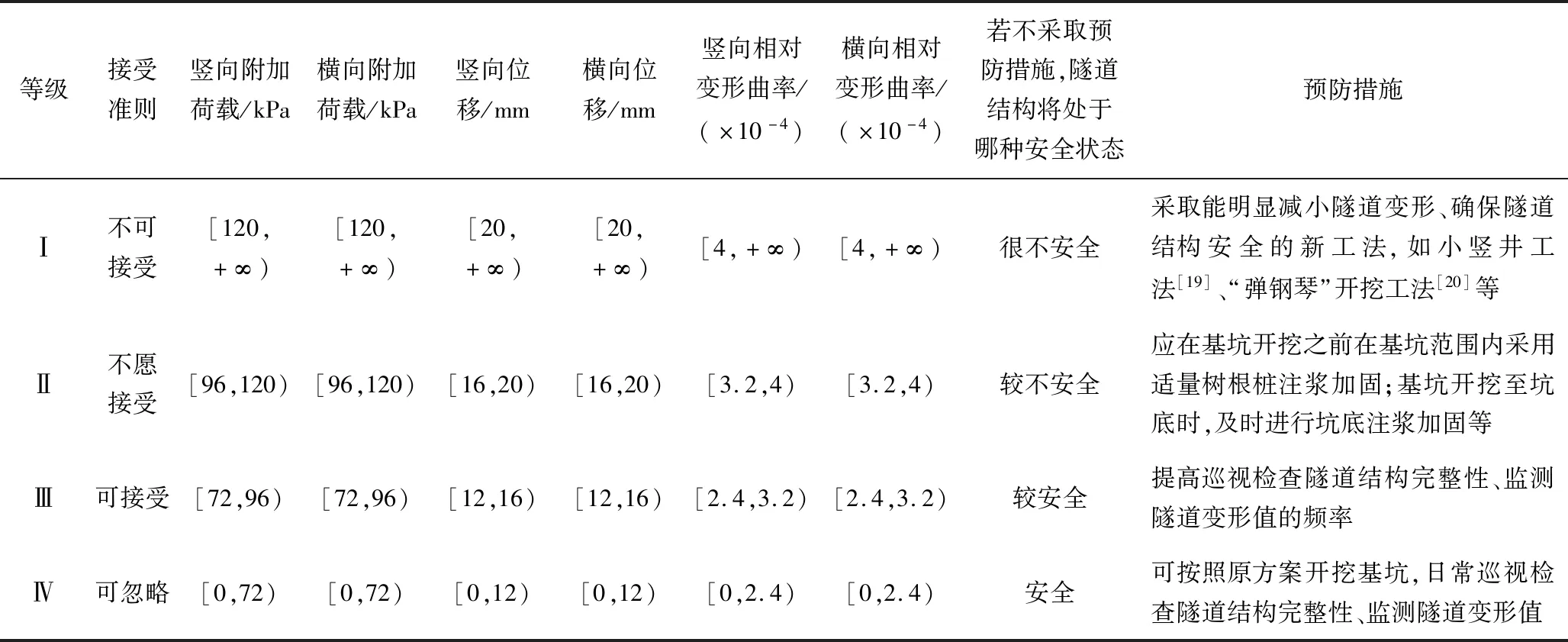
表1 不同因子的風險等級劃分Table 1 Risk rank classification of different factors

各土層物理力學參數取值范圍為：

1)基坑內土層

γ～N(19.1,0.812)(單位：kN/m3)；

ν1～N(0.33,0.0182)；

K0～N(0.45,0.0652)。

2)隧道所在土層

ν2～N(0.30,0.0072)；

Es～N(10.5,1.482)(單位：MPa)。

4.3.1 各土層物理力學參數對6個因子的敏感性分析

每次取其中一個土層物理力學參數變量的μ-2δ、μ-δ、μ、μ+δ、μ+2δ共5個數值進行敏感性分析，其他土層物理力學參數取值均為μ。則各土層物理力學參數對6個因子的敏感性分析結果如圖3所示，μ為平均值，δ為標準差。

由圖3可知：1)附加荷載對γ數值的改變最敏感；2)位移和相對變形曲率對Es數值的改變最敏感；3)附加荷載、位移和相對變形曲率對ν2數值改變的敏感性很低，因此為了減少各級風險發生概率計算結果趨于穩定時所需隨機抽取試驗次數，本文只選取敏感性相對較高參數γ、ν1、K0、Es的取值進行隨機抽取試驗，ν2取值恒為平均值，即0.30。

圖3 各土層物理力學參數對6個因子的敏感性分析Fig.3 Sensitivity analysis of various physics and mechanics parameters of soil layers to six factors

4.3.2 不同因子各級風險發生的概率計算結果分析

如圖4所示，當m=300時，不同因子各級風險發生的概率計算結果趨于穩定。因此，可以取此時的計算結果進行分析。

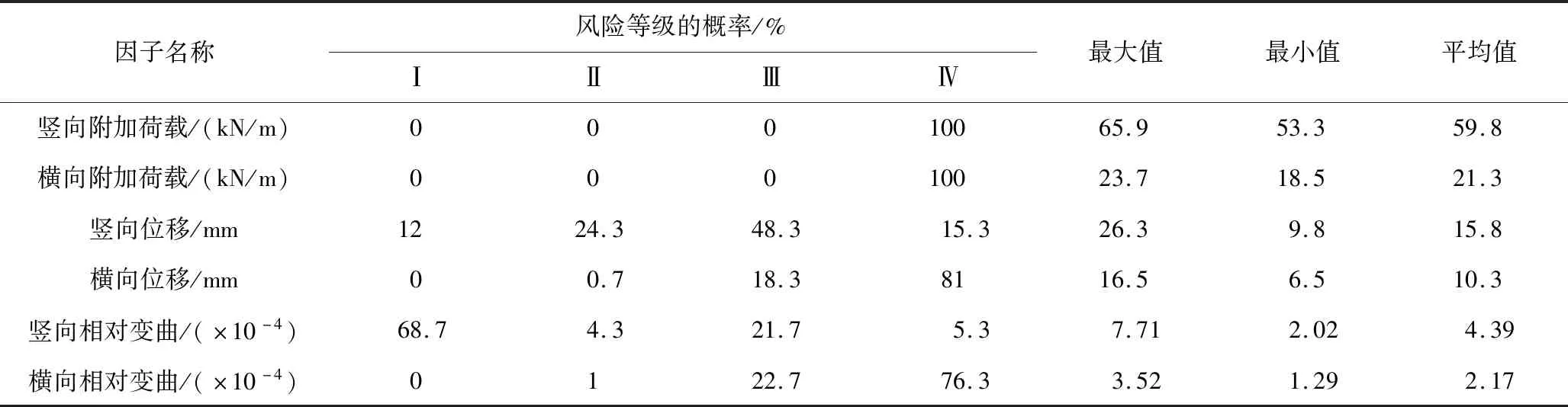
對不同因子各級風險發生的概率計算結果進行統計，統計結果如表2所示。

圖4 不同因子各級風險發生的概率計算結果Fig.4 Calculation results of risk occurrence probability at different levels of different factors

因子名稱風險等級的概率/%ⅠⅡⅢⅣ最大值最小值平均值豎向附加荷載/(kN/m)00010065.953.359.8橫向附加荷載/(kN/m)00010023.718.521.3豎向位移/mm1224.348.315.326.39.815.8橫向位移/mm00.718.38116.56.510.3豎向相對變曲/(×10-4)68.74.321.75.37.712.024.39橫向相對變曲/(×10-4)0122.776.33.521.292.17

由表2可知，基坑放坡開挖卸荷后，1)隧道豎向和橫向附加荷載最大值分別為65.9，23.7 kPa，最小值分別為53.3，18.5 kPa，超過控制值的概率均為0，表明不采取預防措施的情況下，隧道管片不會因豎向或橫向附加荷載過大而發生縱向或軸向開裂的情況；2)隧道豎向位移最大值為26.3 mm，最小值為9.8 mm，超過控制值的概率為12%，因此，必須采取適當的措施減小隧道豎向位移，避免隧道因豎向位移過大導致管片豎向錯開，從而發生漏水、漏泥現象；3)隧道橫向位移最大值分別為16.5 mm，最小值為6.5 mm，最大值并未超過控制值，說明隧道管片不會發生軸向錯開現象；4)隧道豎向相對變形曲率最大值為7.71×10-4，最小值為2.02×10-4，超過控制值的概率高達68.7%。因此，必須采用能極大地減小隧道豎向相對變形曲率的開挖工法[19-20]，否則可能導致隧道管片縱向連接螺栓產生過度彎曲變形而失效，嚴重影響隧道結構的整體性和穩定性；5)隧道橫向相對變形曲率最大值為3.52×10-4，最小值為1.29×10-4，最大值小于控制值。但豎向相對變形曲率超過控制值的概率較高，因此隧道管片軸向連接螺栓很可能不能發揮正常的連接作用。

4.3.3 豎向和橫向2類因子綜合影響下各級風險發生的總概率計算結果分析

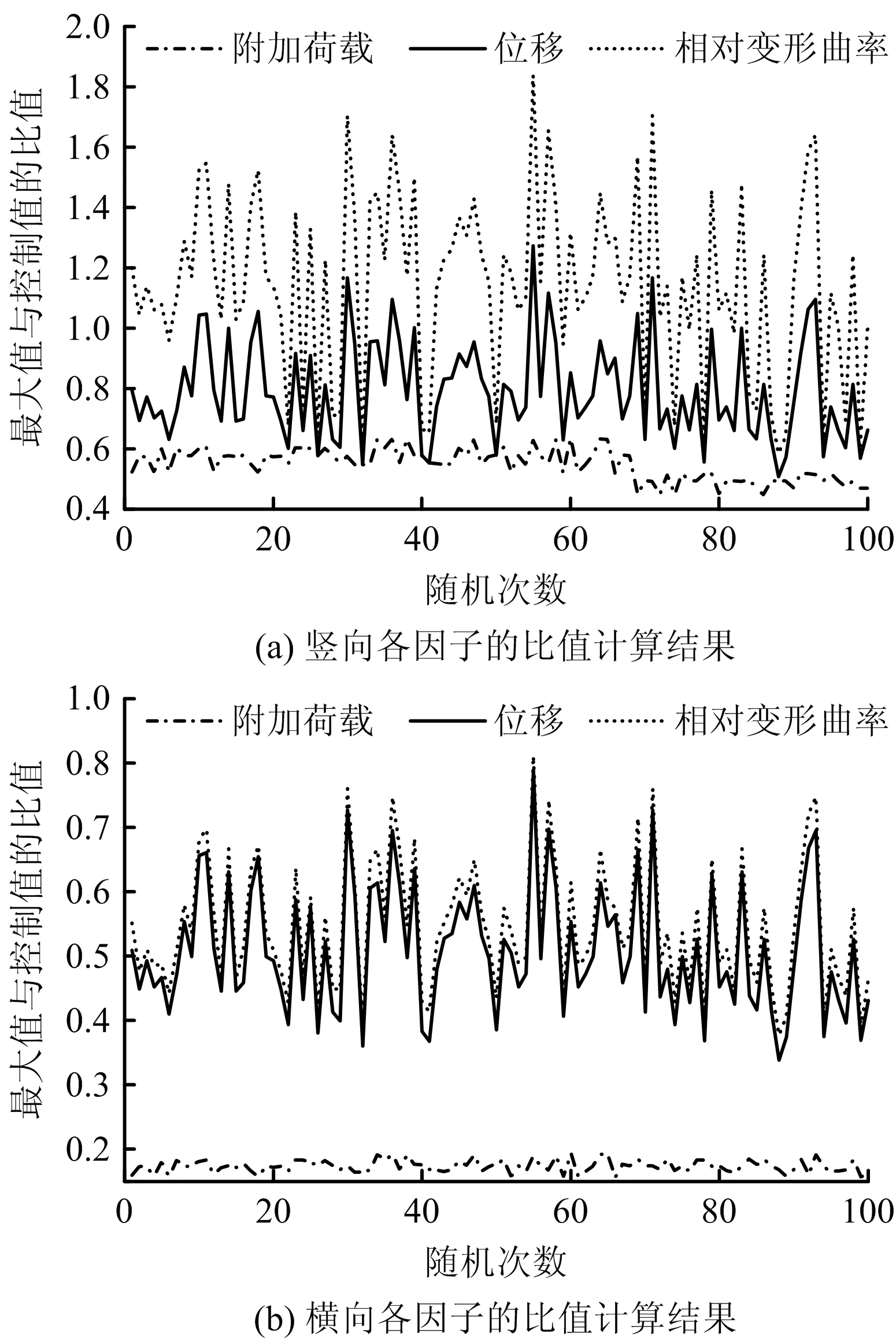
圖5 豎向和橫向各因子的比值計算結果Fig.5 Ratio calculation results of different vertical and lateral factors

由圖5可知，在100次隨機試驗中，豎向和橫向2類因素中比值最大的因子總是相對變形曲率，表明在豎直和水平方向上對隧道結構安全造成最不利影響的因素始終是豎向和橫向相對變形曲率，豎向和橫向相對變形曲率各級風險發生的概率可分別作為豎向和橫向兩類因子各級風險發生的總概率。

由于豎向和橫向2類因子計算公式互不關聯、相互獨立，則可由相互獨立事件的總概率計算公式求出各級風險發生的總概率，即：

(10)

(11)

(12)

(13)

式中：P1，P2，P3，P4分別為Ⅰ，Ⅱ，Ⅲ，Ⅳ級風險發生的總概率；ri,j為第i個因子的j級風險發生的概率。各級風險發生的總概率計算結果如表3所示。

表3 各級風險發生的總概率計算結果Table 3 Calculation results of total probability for risk occurrence at different levels

由表3可知，隧道結構將處于不安全狀態的總概率達到73.27%，處于很不安全狀態的總概率甚至高達68.7%。因此，必須采取等級Ⅰ與Ⅱ中相應的預防措施，降低并管控各單因子的風險，至少將總風險降至等級Ⅲ(可接受)，然后實行等級Ⅲ中相應的預防措施，確保隧道結構安全。

5 結論

1)本文計算方法不僅適用于矩形開挖基坑(基坑放坡坡度為0)，而且可用于放坡開挖基坑，由于實際工程中往往會采用放坡開挖基坑，因此與原來僅限于矩形開挖基坑的計算方法相比，本文計算方法適用范圍更廣、實用性更強；計算坑內土體豎向卸荷引起隧道的附加荷載時，原計算方法假設坑內全部土體被一次性開挖完而直接將豎向卸荷的作用位置移動至坑底，但實際上坑內土體是被多次分小塊開挖完，豎向卸荷的作用位置應在坑內土體原位置，本文計算方法以此為依據對原計算方法做了改進，因此與實際工程更為符合。

2)通過5個土層物理力學參數對各因子的敏感性分析，得到各因子較為敏感的4個參數γ、ν1、K0、Es。基于這4個參數取值的不確定性，利用蒙特卡羅方法預測算例二中隧道不同因子各級風險發生的概率。由風險預測結果可知基坑放坡開挖卸荷后，隧道豎向和橫向附加荷載超過報警值的概率均為0，且隧道橫向位移、橫向相對變形曲率超過報警值的概率較低，僅為0.7%和1%，隧道結構因這4個因子處于不安全狀態的可能性很低；隧道豎向位移和豎向相對變形曲率超過報警值的概率分別為36.3%和73%，并分別有12%和68.7%的概率超過控制值。因此，必須采取相應的措施減小隧道豎向位移和豎向相對變形曲率，避免隧道結構處于不安全狀態；隧道豎向相對變形曲率是隧道結構處于不安全狀態的最主要因子。

3)由豎向和橫向2類因子綜合影響分析可知，豎向和橫向相對變形曲率分別為豎向和橫向2類因子中表征隧道結構安全最具代表性的因子。隧道結構將處于不安全狀態的總概率達到73.27%，其中，將處于不可接受風險(很不安全狀態)的總概率高達68.7%。因此，必須采取相應的預防措施，降低并管控各單因子的風險，至少將總風險降至可接受水平。