非交互式Petri網可覆蓋性驗證的高效實現*

丁如江, 李國強

(上海交通大學 軟件學院,上海 200240)

近年來,基于 Petri網的模型檢測技術已經成功地應用于并發程序的驗證與分析[1-4]中.Petri網是一種適用于描述并發程序的模型,德國學者Sistla[5]首次提出了使用 Petri網來為程序建模的方法.具體來說,可以用Petri網模型中的位置(place)表示程序的狀態,用模型中的遷移(transition)表示程序的執行流,以及每個位置的令牌(token)數表示當前有多少個進程剛好運行到該位置.

并發系統的安全性問題是指系統是否會有可能進入某一錯誤狀態(比如需保證進程互斥的系統發生了多個進程同時運行到某一關鍵位置),規約到Petri網的可覆蓋性問題為:給定一個Petri網和一個狀態M(對應到并發系統中的一個錯誤狀態),是否會有一些由初始狀態M0可達的狀態M′覆蓋了M.如果存在可達狀態覆蓋錯誤狀態M,就表明模型對應的系統不是絕對安全的,系統在理論上會覆蓋這個錯誤狀態.現有的驗證Petri網可覆蓋性的算法大致分為兩類:一類是基于Petri網狀態空間的遍歷,通過搜索Petri網的可達狀態空間來判斷是否覆蓋待驗證狀態M.然而,由于Petri網的狀態空間規模與其位置遷移數是指數級別關系,所以這類算法在面對規模較大的Petri網時都顯得力不從心.比如BFC[4]、MIST、IIC[6]等工具都會有超時的問題存在.第2類是基于約束的,從Petri網的模型結構以及待驗證狀態中提取出約束條件,然后去求解這些約束來驗證可覆蓋性.然而由于約束的表達能力有限,不可能完美地表達出Petri網的可達狀態空間,所以這些約束條件只能成為可覆蓋性問題的必要而非充分條件.因此,這類算法在理論上是不完備的,比如Petrinizer[7]工具只能驗證那些安全的測試用例,對于不安全的測試用例則無法判定.

本文針對非交互式Petri網(communication-free Petri net),又被稱作基本并發進程(basic parallel processes,簡稱BPP),設計并實現了可以高效驗證其可覆蓋性的工具(communication-free Petri net coverability verifier,簡稱CFPCV).BPP在模型上的計算相對簡單,其可覆蓋性問題是NP完備問題[8],同時,它又能為一類并發程序建模并且進行驗證.我們采用基于約束的方法,從非交互式Petri網的模型結構和待驗證狀態中提取出約束,然后將這些約束交給Z3 SMT求解器求解.如果求解器得出無解,則說明不存在任何可達狀態覆蓋待驗證狀態,即待驗證狀態不可覆蓋.而如果求解器有解(可能有多組解),并不能說明待驗證狀態可覆蓋,因為約束條件的表達能力有限,滿足約束條件的狀態并不一定是該非交互式Petri網的可達狀態,需要額外增加子網可標記方法去驗證該狀態是否可達.如果驗證通過,則說明待驗證狀態可覆蓋.如果沒有通過,則需要迭代地去驗證其他滿足約束條件的狀態,直到最終得出結論,這樣就保證了該工具的算法在理論上是完備的,不存在無法判定的情況.同時,只要對我們的約束條件稍加修改,CFPCV就可以很容易地驗證BPP的可達性問題.

我們通過一個實例來說明基于約束驗證 BPP可覆蓋性問題的方法,圖 1展現的是包含兩個進程的并發程序及其對應的非交互式Petri網.

假定該并發程序需要維護一個寫鎖,即同一時刻最多只能有一個進程可以獲取鎖來寫文件,對應到非交互式Petri網為最多只能有1個進程可以處在位置c,所以該非交互式Petri網必須滿足c≤1(即位置c內的令牌數量不大于1)的性質,也就是說,滿足c≥2的狀態都是錯誤狀態.我們通過基于約束的方法來驗證該非交互式Petri網是否會覆蓋滿足c=2的狀態.首先根據BPP的模型要求,每個位置內的令牌數以及每個遷移的觸發次數都必須大于等于 0,可以得到約束集{lock≥0,not lock≥0,c≥0,t1≥0,t2≥0,t3≥0,t4≥0,t5≥0,t6≥0}.然后根據位置和遷移的轉移關系得到約束集{lock=2+t5+t6–t1–t2,not lock=0+t1+t2–t3–t4,c=0+t3+t4–t5–t6}.最后加入待驗證狀態的約束集{c≥2}.將這些約束集合并作為輸入交給Z3 SMT求解器求解,得出一個解{lock=0,not lock=0,c=2,t1=1,t2=1,t3=1,t4=1,t5=0,t6=0}.之后通過子網可標記驗證發現這組解確實是合法解,我們就可以判定該非交互式Petri網可以覆蓋滿足c=2的狀態,從而說明對應的并發程序是不安全的,可能會存在兩個進程同時得到鎖一起寫文件的情況.

本文第1節介紹所用到的背景知識,包括傳統Petri網、非交互式Petri網、可達性和可覆蓋性問題的數學定義,以及本文所使用到的Z3 SMT求解器介紹.第2節介紹驗證非交互式Petri網可覆蓋性的安全性方法以及子網可標記驗證技術.第3節介紹CFPCV的總體技術框架以及使用的算法細節.第4節主要介紹實驗及實驗結果的分析.第5節介紹Petri網可覆蓋性研究的一些相關工作.第6節總結全文,并展望未來的工作.

1 預備知識

1.1 Petri網

Petri網可以用一個四元組N=(P,T,F,M0)來表示,其中,P是Petri網中所有位置的有限集合,T是Petri網中所有遷移的有限集合,F:(P×T)∪(T×F)→{0,1}稱為Petri網的流函數,它表示位置和遷移之間的連接關系.而M0表示該 Petri網的初始狀態.對于x∈P∪T,·x={y∈P∪T|F(y,x)=1},x·={y∈P∪T|F(x,y)=1}.·x記為x的前集或者輸入集,x·記為x的后集或者輸出集.Petri網的狀態M是一個從位置集合P映射到自然數的向量:P→?,該向量內的元素M(p)表示當前狀態下位置p內的令牌數.

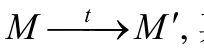
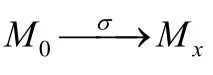
Petri網的可達性問題是指給定一個Petri網N=(P,T,F,M0)和一個狀態M,判斷M∈R(M0)是否成立,即判斷狀態M是否由M0到達;可覆蓋性問題是指給定一個Petri網N=(P,T,F,M0)和一個狀態M,判斷是否存在一個狀態M′∈R(M0),滿足?p∈P,M′(p)≥M(p).如果存在,則稱該 Petri網覆蓋狀態M.

1.2 非交互式Petri網

非交互式Petri網是指滿足?t∈T,|·t|=1,即每個遷移的輸入位置數量為1的Petri網[8].它的可覆蓋性問題復雜度從Petri網的EXPSPACE完備降低到了NP完備.

1.3 SMT求解器

SAT問題被證明是第一個NP完備問題.作為SAT問題的擴展,SMT問題[9]處理的對象是一階邏輯公式,相比于命題邏輯,增加了謂詞和量詞,很大程度上增強了SMT公式的表達能力.用以求解SMT問題的自動化工具稱為SMT求解器.SMT求解技術在有界模型檢測、基于符號執行的程序分析、線性規劃和調度、測試用例生成以及電路設計和驗證等領域有非常廣泛的應用.很多科研機構以及公司都在致力研發正確率高、性能優異的SMT求解器,并且已經成功應用到了具體的領域.目前流行的SMT求解器有:Barcelogic[10]、Beaver[11]、Yices[12]以及Z3[13]等.其中,由微軟公司主導開發的Z3 SMT求解器所支持的理論最多,性能也最好,因此本文使用了Z3 SMT求解器作為我們的求解引擎.

2 安全性方法與子網可標記驗證

本節主要介紹驗證非交互式 Petri網可覆蓋性所用到的安全性方法以及子網可標記驗證技術,在介紹安全性方法之前,我們首先介紹其核心——狀態方程的概念,最后介紹兩個加速剪枝的技巧.

2.1 狀態方程

對于一個給定的非交互式Petri網N=(P,T,F,M0),用一個大小為|P|的列向量M表示N的當前狀態,用一個大小為|T|的列向量X代表遷移序列σ中每個遷移觸發的次數,那么狀態方程表示為

其中,C稱作關聯矩陣,它是一個|P|×|T|大小的矩陣,它的每一項的值按如下方法計算:

顯然,關聯矩陣記錄了該非交互式Petri網中每一個位置與遷移之間的連接關系.而X是遷移序列σ中每個遷移觸發的次數.可以用Parikh映射(Parikh mapping)來表示它們之間的關系:

其中,ω(ti)代表遷移ti在遷移序列σ觸發的次數.

比如對于圖3給定的非交互式Petri網和一個遷移序列σ=t1t2t1t3t2t1,就可以根據狀態方程計算出σ觸發后的新狀態M=[5,3,3,1,–1]T,其中,

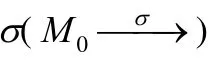
2.2 安全性方法

安全性方法(safety method)是驗證非交互式 Petri網可覆蓋性的基本方法,顧名思義,其目的就是為了驗證非交互式Petri網對應的并發系統是否安全.其基本思想是給定一個非交互式Petri網N和一個性質φ,如果根據狀態方程M=M0+CX得出的所有狀態都不會違反?φ,則該非交互式Petri網一定滿足性質φ.值得注意的是,如果狀態方程得出的某一個狀態M′滿足了?φ,并不能說明該非交互式 Petri網違反性質φ.因為前文有提到,狀態方程得出的狀態空間Set(M)是可達狀態空間R(M0)的超集,所以違反性質φ的狀態M′不一定是該非交互式Petri網的可達狀態.因此,安全性方法在理論上是不完備的,它只能在一個方向進行驗證,這也是安全性方法的局限所在.

本文只討論滿足如下條件的非交互式Petri網.

1) 在任何合法的狀態下,每個位置的令牌數必須大于等于0.

2) 在任何合法的遷移序列中,每個遷移的觸發次數必須大于等于0.

結合狀態方程可以用如下約束條件表示[7]:

安全性方法用約束條件來表達就是將C(N)約束與待驗證性質φ的取反結合,表示為

約束(1)可以表示成多元一次等式和不等式的組合,而 SMT求解器可以很快地求解這些等式與不等式的組合.將約束(1)作為輸入交給SMT求解器求解,得出:

1) 無解,則說明狀態方程得出的狀態都不會違反性質φ,即Set(M)|=φ,又因為R(M0)?Set(M),所以R(M0)|=φ,繼而推出該非交互式Petri網N|=φ.也就說明對應的并發系統是安全的.

2) 有解,則說明存在某狀態M′違反性質φ,但由于Set(M)?R(M0),所以M′不一定是該非交互式Petri網N的可達狀態,因此無法判定N是否滿足性質φ,這也是安全性方法的局限所在.下一小節提出的子網可標記驗證方法,可以有效地判定候選狀態M′是否是N的可達狀態,從而彌補了安全性方法的不足.

2.3 子網可標記驗證

前文介紹了驗證非交互式Petri網可覆蓋性的安全性方法,雖然該算法借助于SMT求解器可以很高效地運行,但是該算法在理論上卻不完備,只能驗證非交互式Petri網N滿足性質φ,卻無法得出N不滿足性質φ的結論.原因是安全性方法依賴于狀態方程,對于狀態方程得出的候選狀態M′,我們無法判斷M′是否是N的可達狀態.

而子網可標記驗證可以嚴謹地判定某個狀態M′是否是非交互式Petri網的可達狀態,從而可以彌補安全性方法的不足,在驗證非交互式Petri網可覆蓋性時達到理論完備.

在介紹如何使用子網可標記驗證判定狀態M′是否為非交互式Petri網的可達狀態之前,需要引入如下的定義、引理與定理[8].

定義 1.給定一個 Petri網N=(P,T,F)和一個遷移集合T的子集S,那么由S構成的N的子網NS=(PS,S,FS).

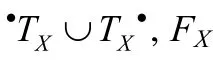
定義2.給定一個Petri網N=(P,T,F,M0)和一個狀態M:

· 如果存在一個狀態M′,使得M′由M可達,且M′(p)>0(其中,p∈P),則稱位置p由狀態M可標記.

· 對于N的子網N′=(P′,T′,F′,M0′),如果N上的狀態M在N′上的投影為M′,且位置p(其中,p∈P′)由狀態M′可標記,則稱位置p在N′上由M可標記.

引理1.給定一個非交互式Petri網N和它的一個狀態M,一個位置p由狀態M可標記當且僅當N中存在一條從p′到p的路徑,其中,p′滿足M(p′)>0.

引理1給出了一個在非交互式Petri網N上,快速判定位置p是否由狀態M可標記的方法,即如果在M狀態下內部令牌數大于0的某個位置p′,存在一條到位置p的路徑,那么就可以說明位置p在N上由M可標記.也就是說,對于M狀態下內部令牌數大于 0的位置,從這些位置經過遷移可以到達的位置都是由狀態M可標記的.

例如,針對圖3所示的Petri網,給定向量X=[1,0,0]T,則子網NX如圖4所示,包含p1,p2,p3,p4這4個位置,t1一個遷移以及它們之間的流關系.在子網NX中,顯然,p1,p2,p3,p4都由狀態M0可標記,因為M0狀態下,p4內的令牌數大于0,且p1,p2,p3都由p4可達.

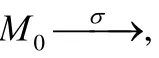
2) 子網NX內的任一位置都能在NX上由M0可標記.

定理 1給出了判定一個遷移觸發次數的向量X是否合法的充要條件,即在向量X的作用下,該非交互式Petri網的每個位置內的令牌數必須大于等于0,而且子網NX內的所有位置都必須由M0可標記.結合定義2和引理 1,則定理 1的條件 2)可以表述為:NX內的所有位置都必須由M0X可標記,即?p∈PX,NX中都存在一條從p′(p′∈PX)到p的路徑,其中,p′滿足M0X(p′)＞0.如果X滿足定理1的兩個條件,則可以說明X合法,那么X作用下的狀態M就是可達狀態,因為M可以由M0通過σ到達.這樣一來,我們就將判定非交互式Petri網上某個狀態是否可達規約到其對應的遷移觸發次數向量X是否合法,使得問題變得更加具體,更加便于操作.

對于傳統的 Petri網,我們很難判定某個狀態是否是可達狀態.而對于非交互式 Petri網,結合狀態方程與定理 1,可以有效地判定某個狀態是否可達.我們可以通過狀態方程M′=M0+CX′求得M′對應的解X′(可能有多個解),然后再去驗證X′是否合法,如果合法,就可以得出M′可達的結論.而如果不合法,則可以迭代地去驗證其余解,如果所有的解都不合法,就可以斷定M′不可達.

在安全性方法中,任何非交互式Petri網N=(P,T,F,M0)都必須滿足C(N)約束,規定了在任何狀態下每個位置內的令牌數都必須大于等于0,所以,定理1的第1個條件天然滿足.至于第2個條件,在安全性方法中,如果約束(1)有解(可能有多組解),即?M′∈Set(M),?φ(M′)成立.我們可以通過定理 1 來判定M′是否可達,即判定其對應的X′是否合法.這樣就可以嚴格地去驗證非交互式Petri網是否覆蓋某個錯誤狀態,使得算法在理論上達到完備.

結合安全性方法與子網可標記驗證,驗證非交互式Petri網可覆蓋性的方法可以表述如下.

以太網INTERNET模塊程序主要包括通過Xbee協調器對Xbee終端數據的接收與發送，以太網模塊W5100數據上傳與服務器控制命令的接收，其流程圖如圖4所示.以太網模塊程序首先配置網絡IP地址、DNS服務器等數據，再利用LEWEI50云平臺TCP通訊協議庫＜LeweiTcpClient.h＞實現數據上傳、遠程開關的反向控制.

從非交互式Petri網N和待驗證性質φ中獲取約束條件C(P,T,F,M0)^?φ,作為SMT求解器的輸入進行求解.

1) 無解,即約束條件不滿足,說明該非交互式Petri網的所有狀態都滿足性質φ,N不會覆蓋滿足性質?φ的錯誤狀態.

2) 有解,即?M′∈Set(M),?φ(M′)成立.我們需要去驗證M′對應的X′是否滿足定理 1 的第 2 個條件.

a) 若滿足,說明?φ會被一個可達狀態滿足,表明N不滿足性質φ,N會覆蓋滿足性質?φ的錯誤狀態.

b) 若不滿足,說明滿足?φ的狀態M′不可達.由于滿足約束C(P,T,F,M0)^?φ的狀態可能有多個,所以需要加上新的約束條件剔除狀態M′,繼續交給SMT求解器求解,進行下一次迭代(注:由于約束(1)中等式的數量可能少于變量的個數,且約束中存在不等式,所以約束(1)的解的數量可能是無限的,而且可能存在需要無數次迭代的極端情況.不過,從之后的測試發現,多次迭代的情況非常少.當然,約束(1)解的數量并不等于迭代的次數,因為每次迭代并不一定只排除一個解,也可能是一組甚至無數解,可以參考第 3.3節中的實例,而排除解的數量在不同的模型中也互不相同,所以約束(1)解的數量和迭代次數之間的關系并不能用確切的表達式來表達.甚至可能存在約束(1)解的數量無限,但是只需要幾次迭代即可成功驗證的情況).

2.4 剪枝技巧

因為對于 SMT求解器的每組解,我們都需要驗證其是否符合定理 1的條件 2),為了減少算法的迭代次數,我們可以增加兩種剪枝加速的方法.

1) 在給定的非交互Petri網N=(P,T,F,M0)中,對于那些滿足M0(p)>0的位置,它們的輸出遷移必須至少有一個觸發次數大于0.約束化為Constraints1.

因為我們要驗證每組解是否符合定理1的條件2),也就是子網內的每個位置都要由M0可標記.由引理1可知,該子網內至少有一個位置p滿足M0(p)>0.因此,如果Constraint1無法滿足,也就是說,滿足M0(p)>0的位置p根本沒有路徑“出去”,則子網內的其他位置p′都無法由M0可標記.

2) 在給定的非交互Petri網N=(P,T,F,M0)中,如果存在這樣的位置,InitPlace集合中的任意一個位置都不存在一條到它的路徑,那么它的輸入和輸出遷移發生的次數都為0.約束化為Constraints2.

因為對于這些無法從InitTransition中的位置到達的位置,它們在任何狀態子網上都是無法由M0可標記的,如果它們的輸入或者輸出遷移發生的次數大于 0,那么子網就必須將這些位置包含進去,那么該子網就不可能滿足定理1的條件2).

使用上述兩種剪枝技巧,可以有效地減少算法的迭代次數,使得驗證更加高效、實用.

3 CFPCV工具技術框架

我們采用基于約束的方法,實現了可以高效驗證非交互式Petri網可覆蓋性的工具CFPCV,它在安全性方法的基礎上,加上子網可標記驗證,從而使得該算法在理論上完備.本節主要介紹 CFPCV工具的技術架構以及使用到的具體算法.

3.1 技術架構

本文的技術方案如圖5所示.主要分為約束提取、約束求解、候選解驗證、增加約束進行迭代這4個部分.具體內容如下.

1) 首先根據給定的非交互Petri網模型N=(P,T,F,M0)得到一些模型的基本約束,例如每個位置內的令牌數必須大于等于 0,每個遷移發生的次數必須大于等于 0,再根據需要驗證的狀態M得到狀態約束,例如待驗證性質為p1=1&p2=1,則約束p1≥1&p2≥1可以覆蓋滿足此性質的狀態.

2) 將步驟1)得到的約束條件和剪枝技巧合并為約束文件,作為輸入交給SMT求解器求解.

3) 如果無解,則表明不存在滿足這些約束條件的狀態,也就是說,N不能覆蓋狀態M′;如果有解并不能代表N覆蓋狀態M,只能代表M′滿足這些約束條件,還必須驗證M′由M0可達,即需要將狀態M′從狀態方程的狀態空間壓縮到該非交互式Petri網的可達狀態空間內.

4) 如果驗證出M′狀態確實由M0可達,則可以表明N覆蓋M;如果不可達,說明SMT求解器求出的這組解(基于約束條件可能有很多組解,求解器每次只給出一組解)不滿足要求.需要將狀態M′代表的這一類狀態剔除,即生成新的約束加入到約束文件中,重復步驟3)和步驟4),直到程序得到解退出為止.

3.2 算法實現

CFPCV工具使用到的核心算法偽代碼如下.

關于算法的邏輯,前文已經解釋清楚,主要分為約束提取、約束求解、候選解驗證、增加約束進行迭代這4個部分,這里不再贅述.其中,第 8行的代碼表示提取新約束來剔除子網SN所代表的一系列解.比如,T={t1,t2,t3,t4},X={1,0,3,1}.那么,SN就是根據t1,t3,t4這3個遷移構成的子網,如果子網SN不滿足定理1的條件2),則在下一次迭代中,必須增加約束將SN所代表的一系列解剔除,即新約束δ為not(t1>0 &t2=0 &t3>0 &t4>0).

3.3 算法求解示例

我們可以通過一個實例再進一步更加直觀、清晰地認識這一算法,對于圖8給定的非交互式Petri網和帶驗證性質φ(p1+p3<3),安全性約束C(P,T,F,M0)^?φ為

p1,p2,p3,p4≥0

t1,t2,t3,t4,t5≥0

p1=0+t5

p2=1+t3+t4

p3=0+t3+t4+t5

p4=0+t1+t2+t3+t4–t5

p1+p3≥3

兩種剪枝約束Constraint1(2)和Constraint2(3).

t2>0

將上述約束作為輸入交給SMT求解器求解,有解,解ModelA1為

p1=0,p2=3,p3=3,p4=4

t1=0,t2=1,t3=0,t4=3,t5=0

所以X1=(0,1,0,3,0),構成的子網NX1如圖6所示.

顯然,該子網中只有p2,p4由M0可標記,因此需要增加新約束δnot(t1=0 &t2>0 &t3=0 &t4>0 &t5=0),剔除該子網進行下一次迭代,下一次迭代的約束即為

p1,p2,p3,p4≥0

t1,t2,t3,t4,t5≥0

p1=0+t5

p2=1+t3+t4

p3=0+t3+t4+t5

p4=0+t1+t2+t3+t4–t5

p1+p3≥3

t2>0

not(t1=0 &t2>0 &t3=0 &t4>0 &t5=0)

將新的約束文件作為輸入交給SMT求解器求解,依然有解,解ModelA2為

p1=1

p2,p2,p3=3

t1,t2,t3,t4,t5=1

所以X2=(1,1,1,1,1),而由NX2構成的子網如圖7所示.

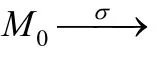
4 實驗及結果分析

由于現有的驗證可覆蓋性問題的工具都是針對傳統 Petri網的,它們所使用到的標準測試集也都是傳統Petri網,所以這些測試集對于CFPCV工具的測試不再適用.因此,針對非交互式Petri網,我們隨機生成了3組非交互式Petri網的測試用例,它們的位置和遷移數規模分別是1～10、1～100、1～1000.我們主要從成功率、迭代次數、性能比這3個方面對CFPCV進行了評測.我們主要與Petrinizer、MIST這兩個工具進行了比較,Petrinizer工具是通過提取約束并求解的方法來驗證傳統 Petri網的可覆蓋性問題,與 CFPCV一樣,它也是采用安全性方法來獲得約束.不過,正如前文所述,安全性方法在理論上是不完備的,其只能驗證那些覆蓋的用例,對于不覆蓋的用例則無能為力.但從文獻[7]中的實驗結果來看,Petrinizer在應對一些特定的測試集時仍然有不錯的成功率.而 MIST工具是采用狀態空間探索的方法,其內部集成了多種驗證算法,包括從待驗證狀態反向探索狀態空間的backward[14]算法,以及先對原Petri網模型進行抽象精化(abstraction refinement)來縮小模型規模,然后再結合前驅和反向探索狀態空間來進行驗證的 ic4pn[15]算法、tsi[15]算法和 eec[16]算法.盡管增加了抽象精化的過程來縮小模型的規模,但是對于隨機模型這個過程的效果甚微,依然會有狀態爆炸(state explosion)的問題存在.

4.1 成功率

我們將隨機生成的3組測試用例作為輸入交給CFPCV、Petrinizer、MIST工具求解,后兩種工具都是驗證傳統Petri網可覆蓋性的工具,所以它們肯定也可以驗證非交互式Petri網的可覆蓋性問題.我們分別比較了這3種工具在每組測試用例下的成功率,見表1～表3(注:Positive表示滿足性質φ,Negative表示不滿足,Timeout表示超時,Don’t know表示無法判定,Success rate表示成功率).

從3張表可以發現,Petrinizer工具的成功率最低,因為Petrinizer使用到的方法也是安全性方法,但因其針對傳統Petri網,并沒有子網可標記驗證來保證候選解是正確解,所以該工具使用到的算法在理論上不完備,可能存在其無法判定的情況,所以對于隨機生成的測試用例,有大量的測試用例其無法判定,因此成功率在 3種工具中最低,在第3組測試用例上只有4.6%的成功率.而MIST工具是基于Petri網可達狀態空間的搜索,由于Petri網的可達狀態空間可能很大,所以該工具經常發生超時情況,對于規模較大的輸入,超時情況更加嚴重.所以,對于隨機生成的測試用例,MIST工具超時最多,而且隨著測試用例規模的擴大,其超時情況變得非常嚴重,成功率直接從100%下降到了46.9%.顯然,CFPCV工具的成功率最為優異,對于3組測試用例成功率都在99%以上.

Table 1 Success rate of the 3 tools in test cases which scales of place and transition are between 1 to 10表1 測試用例位置遷移數規模1～10之間3種工具的成功率

Table 2 Success rate of the 3 tools in test cases which scales of place and transition are between 1 to 100表2 測試用例位置遷移數規模1～100之間3種工具的成功率

Table 3 Success rate of the 3 tools in test cases which scales of place and transition are between 1 to 1000表3 測試用例位置遷移數規模1～1000之間3種工具的成功率

4.2 迭代次數

因為 CFPCV 使用到的算法是基于迭代的,需要在每次迭代中驗證候選解是否是正確解,如果不是,則需要增加約束繼續迭代求解,所以算法的迭代次數直接決定了算法的運行效率.如果迭代次數過多,就可能發生超時的情況.我們記錄了每組測試用例算法的迭代次數,見表4.

由表 4可以發現,對于絕大多數(2587+397)測試用例,只需要 1～2次迭代即可得解,只有極個別的測試用例需要10次以上的迭代(12次2個,16次1個,超時10個).因為只需要很少的迭代次數即可得解,所以CFPCV工具的運行效率理應很高.

Table 4 Iteration time of CFPCV表4 CFPCV運行迭代次數

4.3 性能比

因為CFPCV和Petrinizer都用到了安全性方法,且Petrinizer的性能也非常高,只不過其成功率較低,所以我們比較了3組測試用例下這兩種工具的性能(未比較MIST是因為MIST超時情況嚴重,所以其性能自然較低),性能比如圖9～圖11所示,單位為s.

由圖9～圖11可知,Petrinizer和CFPCV性能相當,大部分測試用例兩種工具在20s內得解.圖中箭頭標注的點分為兩類,一類是CFPCV需要的較多的迭代才可得解,因此這些點代表的測試用例CFPCV運行較慢.另一類是兩種工具都超時(圖11右上角的8個點),原因是因為SMT求解器求解約束超時,這種情況是合理的,因為有些約束求解問題(比如SAT問題)就是NP完備問題,可能存在一些測試用例SMT求解器根本無法求解,因此兩種工具都發生了超時的情況.因為Petrinizer沒有驗證候選解的迭代過程,所以Petrinizer的性能理應比CFPCV要好.但是由第 4.2節迭代次數的記錄來看,對于絕大多數測試用例,CFPCV只需要一兩次迭代即可得解,因此CFPCV的性能和Petrinizerx相差無幾.考慮到第4.1節提到的CFPCV極高的成功率,這樣的性能是非常令人欣慰的.

5 相關工作

Petri網的可覆蓋性問題雖然已被證明是EXPSPACE完備問題[17,18],BPP的可達性以及可覆蓋性問題也都被證明是NP完備問題[3],但是近年來學術界依然提出了很多解決該問題的算法,它們可以大致分為兩類:第1類就是基于狀態空間的探索.由Karp和Miller(簡稱KM)提出的Karp and Miller procedure[17]是第一個可以驗證Petri網可覆蓋性的完備算法,它的主要思想是從Petri網的初始狀態前驅探索(forward exploration)狀態空間,不斷加入可以覆蓋前一狀態的新狀態來構造 Petri網的覆蓋樹,然后判斷待驗證狀態是否在該覆蓋樹上來進行驗證.但是,由于 Petri網的可達狀態可以無限制地增長,導致覆蓋樹的規模可能非常之大,所以這個構造過程通常比較低效,它具有非原始遞歸最壞情況的復雜度.這項技術已在 TINA-KM[19]工具上實現,可想而知,該工具在處理狀態空間較大的模型時效率很低.另外,這項技術的一種優化方法就是構造 Petri網的最小覆蓋集(minimal coverability sets)[20]而非覆蓋樹,最小覆蓋集已被證明是存在且有限的[21],而且其規模要遠小于覆蓋樹的規模,所以其構造效率有了較大的提升,這項技術已在 Pep[22]工具上實現.另外,還有反向探索(backward exploration)[23]狀態空間的算法,就是從待驗證狀態反向探索狀態空間,直到到達初始狀態為止,這項技術已在工具 IST-BC和PETR-BC[24]上實現,不過,反向探索和前驅探索本質上沒有太大的區別,所以算法效率并沒有顯著的提升.當然,還有將前驅探索和反向探索結合[25,26]的算法,分別從初始狀態前驅探索狀態空間和從待驗證狀態反向探索狀態空間,直到兩條探索路徑觸碰為止,這項技術已在工具BFC上實現,性能得到了較大的提升.文獻[16]中提出的‘Expand, Enlarge and Check’方法通過并發地構造兩個Petri網的近似序列來驗證可覆蓋性,第1個序列是系統的向下近似,它可以用來判定覆蓋的實例,另外一個序列是系統的向上近似,用來判定那些不覆蓋的實例.這項技術已在工具 MIST上實現.MIST內部集成了多種算法,不過,它們的思路大體一致,都是先對原模型進行一層抽象來縮小模型的規模,然后對抽象后的模型通過前驅探索和反向探索結合的方法來加以驗證.另外一類是基于約束的方法.其主要思想與本文的算法類似,都是用約束條件來表達Petri網的性質,通過求解約束來驗證可覆蓋性.然而,由于約束的表達能力有限,不可能準確表述出 Petri網的可達狀態空間,所以這些約束條件只能成為可覆蓋性問題的必要條件而非充分條件.因此這類算法在理論上是不完備的,比如 Petrinizer[7]工具,它是通過安全性方法來提取約束并求解來進行驗證,不過,由于安全性方法在理論上不完備,所以它只能驗證那些不覆蓋的測試用例,對于覆蓋的測試用例則無法驗證.

除此之外,并發程序的性質也可以通過基于 Petri網的模型檢測技術來分析,使用 TCTL(時間計算樹邏輯)[27]來描述待驗證性質,通過檢測 Petri網的遷移發生序列來驗證模型是否滿足這些性質.其具體思路是先構造包含待驗證性質取反語義序列的Büchi自動機,然后再計算Petri網可達圖和自動機的乘積圖.若將乘積圖看成一個有向圖,則模型檢測的問題等價于檢測乘積圖中是否包含一個從初始狀態可達的最大強連通分量,且在該強連通分量中包含了一個接受狀態.對于安全性一類的性質來說,等價于檢測乘積圖中是否存在一條從初始節點到接受節點的路徑.對于活性一類的性質來說,等價于檢測乘積圖中是否存在由初始節點可達的包含接受節點的環.但是,基于 Petri網的模型檢測技術也會受到狀態爆炸問題的困擾,因為 Petri網模型的狀態空間通常非常之大,甚至無界,所以 Petri網的模型檢測問題難度非常之大,其上的很多邏輯算子都不存在多項式時間算法.比如EG/AF(即我們通常所說的活性)邏輯在Petri網和BPP上都是不可判定的,EF邏輯在Petri網同樣不可判定,在BPP上雖然可判定,但也擁有PSPACE完備的復雜度[28].所以,傳統的基于Petri網的模型檢測技術在驗證并發程序的性質時存在較大的局限性.

6 總結及未來的工作

本文設計并實現了可以高效驗證非交互式Petri網可覆蓋性的工具CFPCV,它在驗證傳統Petri網可覆蓋性使用到的安全性方法的基礎上,增加了只對非交互式Petri網適用的子網可標記驗證,從而保證了其解的正確性,并且通過實驗驗證了該工具具有較高的成功率以及不錯的性能.

由于業界缺乏針對非交互 Petri網可覆蓋性驗證的標準測試集,所以本文測試所使用測試集都是隨機產生的.未來會使用數量更多以及質量更高的測試集進行測試,以驗證 CFPCV的表現是否依然優秀.另外,其實除了本文所提的剪枝方法以外,還有一種叫作阱(trap)約束[29]的技巧可以進行加速,不過我們通過測試發現,阱約束的表現卻不盡人意,可能和我們測試集的隨機性有關.未來業界若有質量較高的測試集公開,我們會在算法上增加阱約束進行測試,如果性能得到提升,則將加以改進.

未來,我們也會在BPP上做模型檢測,雖然第5節提到BPP上的模型檢測問題難度很大,但是我們如果做有界模型檢測,比如將某個性質在無限的轉移序列上都要成立限定為在k(k為大于0的自然數)步轉移內成立,同時也保證這樣的性質具有一定的實際意義,那么問題的復雜度將大幅下降.同樣通過提取約束,使用 SMT求解器求解約束的方法,BPP上的有界模型檢測問題可能會有很高效的解決方案.