基于SVM的多項式循環程序秩函數生成*

李 軼, 蔡天訓, 樊建峰,3, 吳文淵, 馮 勇

1(中國科學院 重慶綠色智能技術研究院 自動推理與認知重慶市重點實驗室,重慶 400714)

2(薩基姆通訊(深圳)有限公司,廣東 深圳 518000)

3(中國科學院大學 計算機科學與技術學院,北京 100093)

循環程序的終止性分析是程序驗證的一個重要研究分支.在現代程序設計中,幾乎所有的程序都會含有循環.然而,即使是簡單的循環程序,也很容易出錯.循環中的很多錯誤往往需要執行多次或在某些特定情況下才能被發現.因此,確保循環程序是可終止的是保障軟件能夠可靠運行的一個必要條件.盡管程序終止性問題早已被證明是一個不可判定問題[1,2].但是人們發現,具有某些特征的循環程序的終止性是可判定的.如:Tiwari在2004年證明了一類線性循環程序在實數域上的終止性是可判定[3].這類程序的終止性在文獻[4-7]中被重新考慮.此外,Zhan等人在文獻[8]中考慮了循環條件為等式的多項式程序的終止性問題,并給出了該類程序可終止和不可終止的充分判準.在文獻[9]中,Zhang等人建立了針對程序終止性驗證的高級自動機算法.在循環非終止研究方面,Zhang給出了一種能夠檢測出簡單循環中出現死循環的充分條件[10].針對確定型線性賦值循環程序,Leike等人在文獻[11]中給出了GNTA條件去探測這類循環的不可終止性.

秩函數法是證明循環程序可終止性的主要方法.給定一個循環程序,倘若它的秩函數被找到,則表明該循環是終止的.為計算秩函數方便起見,人們往往計算多項式型的秩函數.根據多項式秩函數的次數可以將多項式秩函數分為線性秩函數和非線性多項式秩函數.

在線性秩函數研究方面,已有大量工作.譬如,2001年,Colón和Sipma通過凸多面體理論以及Farkas’ Lemma給出了一種計算線性秩函數的方法[12,13].2004年,Podelski和Rybalcheko提出了一種完備的方法來構造線性約束的單分支循環程序的線性秩函數[14].2012年,Bagnara等人[15]研究了線性程序的線性秩函數的計算復雜度問題.在2013年,他們提出了最終的線性秩函數(eventual ranking function)這一概念[16],并通過合成最終的線性秩函數來證明單分支線性約束循環程序的終止性.該方法首先利用一個單調增函數對循環程序的狀態空間進行劃分,然后利用Farkas’ Lemma來合成最終的秩函數.文獻[17]將最終的線性秩函數進行了推廣,提出了深度為L的最終線性秩函數.2014年,Leike等人針對線性循環程序,給出了包括多階段秩函數在內的多個秩函數定義[18].2017年,Ben-Amram等人[19]對多階段秩函數進行了進一步的研究,給出了一個能夠在多項式時間內合成多階段秩函數的方法.同時,他們還指出了多階段秩函數和線性字典序秩函數(lexicographic linear ranking function)、嵌套秩函數(nested ranking function)之間的相互聯系.相較于線性秩函數的研究,非線性多項式秩函數合成方面的工作較少,主要有以下幾篇文獻討論了非線性多項式秩函數的計算.Chen等人[20]利用柱形代數分解(CAD)算法給出了一種合成非線性多項式秩函數的方法.該方法首先設定循環程序的非線性秩函數模板,然后將秩函數合成問題轉化為半代數系統求解問題,從而可利用符號計算工具DISCOVERER和QEPCAD來求解半代數系統,最終得出非線性秩函數模板中參數的解.此外,文獻[21,22]等人通過利用半正定規劃 SDP工具來計算非線性多項式秩函數.

但程序的秩函數未必是多項式的.也即,可以構造一個循環程序,它并沒有多項式秩函數但具有其他形式的秩函數[23].因此,當給定程序沒有多項式秩函數時,我們還不能說它是不可終止的,因為它有可能有其他形式的秩函數.在本文中,我們主要研究下面給出的單重無條件分支的循環程序:

這里,p(x,z)=(p1(x,z),...,ps(x,z)),F(x,z)=(f1(x,z),...,fn(x,z)),且對任意的i∈[1,s],pi(x,z)∈Hn+1,di,對任意的j∈[1,n],fi(x,z)∈Hn+1,d.這里,對任意兩個整數a,b且a≤b,記[a,b]={a,a+ 1,…,b-1,b},由文獻[3,22]中的定理可知,程序與程序P在終止性上是等價的.

因此,不失一般性,本文主要分析下列齊次多項式循環程序終止性.

在下文中,我們將建立新的方法去探測程序Q的秩函數.該方法的主要思路是:將秩函數計算問題歸結為二分類問題,然后利用機器學習中的支持向量機(SVM)算法[24,25]來合成所需秩函數,最終驗證合成的秩函數是否滿足秩函數定義.相較于當前的基于 CAD或 SDP的多項式秩函數計算方法,本文的主要貢獻在于提出的基于SVM 的方法用于計算非多項式型秩函數——代數分式型秩函數,從而將秩函數的研究從多項式型秩函數擴展到代數分式型秩函數,擴大了可計算秩函數類型的范圍.

本文第1節介紹秩函數、支持向量機等相關概念.第2節建立基于SVM的秩函數探測算法,并通過實例詳細闡述該算法.第3節給出更多實驗.第4節總結全文.

1 預備知識

1.1 秩函數

定義1.記號同上.給定齊次多項式循環程序Q.令ρ(x)為一個n元函數.ρ(x)被稱為程序Q的秩函數,如果下列條件被滿足:

則ρ(x)為程序Q的秩函數.

1.2 支持向量機

在樣本空間中,劃分超平面可用線性方程aTx+k=0來描述,其中,a=(a1,…,ad)是超平面的法向量,k是截距項.支持向量機可用于找到最“居中”的那一個超平面.如圖1所示,支持向量機可以找到劃分超平面aTx+k=0,該超平面將圖中的兩類樣本點劃分開,其中,落在aTx+k=1和aTx+k=-1上的點叫作支持向量.支持向量機的求解通常使用SMO算法[24]來實現.LIBSVM[25]是一個關于SVM的集成軟件包,由臺灣大學的Chih-Wei Hsu、Chih-Chung Chang以及Chih-Jen Lin編寫完成.軟件的主要部分采用C語言編寫完成,可在MATLAB上調用.本文的主要計算部分即采用該軟件包完成.

2 主要結果

本節闡述如何將型如程序Q的秩函數計算問題歸結為二分類問題,以便可以利用支持向量機(SVM)工具來計算得到一個候選秩函數,最后再對該候選秩函數進行驗證,以檢驗其是否滿足秩函數的兩個條件(a)和(c).

一般地,計算程序Q的秩函數,需要首先預設一個秩函數模板.秩函數模板形式可以是多種多樣的.但為了方便計算,人們常將秩函數模板設定為多項式模板.但是,由于程序Q是齊次多項式程序,即其中的所有表達式都是齊次多項式的,因此下面的定理告訴我們,程序Q沒有多項式秩函數.

定理2.記號同上.程序Q沒有多項式秩函數.

這顯然與式(3)矛盾.故程序Q沒有多項式秩函數.

2.1 程序Q的秩函數計算歸結為二分類問題

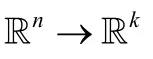
下面的命題表明,若T(x)在Ω上有定義,那么,函數T(x)為有界函數.也即,存在正數δ,使得對任意的x∈Ω有|T(x)|≤δ.

命題3.記號同上.若T(x)在Ω上有定義,那么,T(x)在Ω上有界.

證明:既然T(x)在Ω上有定義,則對Ω中任意一點x,T(x)中各個分量的分母均不會為0.考慮T(x)中第v段,即

這里,

顯然有,

既然T(x),U(x)可被看作是?n→?k映射,若它們在Ω上有定義,則記

根據命題 3,若T(x)在Ω上有定義,那么T(Ω)是?k空間中的有界域.倘若存在某a∈?k,使得連續函數L(u)=aT?u在U(Ω)上有下界 1,即

那么,根據U(Ω)的定義有,

根據上述向量a,構造T(Ω)上的連續函數L′(t) =aT?t.既然T(Ω)有界,故L′(t)在T(Ω)上必有下確界,即存在c,使得?t∈T(Ω) ?L′(t)=aT?t≥c.根據T(Ω)的定義,上式等價于

令ρ(x)=aT?T(x)-c.不難看出,上述式(6)對應于秩函數定義中的條件(c),式(7)對應于條件(a).因此,根據式(6)和式(7)以及秩函數定義,易知ρ(x)=aT?T(x)-c恰好是程序Q的秩函數,且是代數分式型的秩函數.從上述分析可以看出,若使得式(5)或者式(6)成立的向量a被找到,那么式(7)自然成立,從而可以構造得到程序Q的秩函數ρ(x)=aT?T(x)-c.因此,計算程序Q的秩函數,我們可以通過計算可滿足式(5)或式(6)的向量a來得到.由此可得下列命題.

命題4.記號同上.若存在aT使得?u∈U(Ω)?L(u)=aT?u≥1,那么程序Q有代數分式秩函數.要尋找使得式(5)成立的向量aT,我們可先對Ω的像集U(Ω)進行分析.

限制條件(C1)成立等價于O?U(Ω ).

命題5.記號同上.假設U(x)在Ω上有定義.倘若?k空間中的原點O?U(Ω),那么,計算使得式(5)成立的向量aT的問題就等價于:在空間?k中尋找可將原點O∈?k與像集U( Ω )∈?k嚴格分離的超平面.

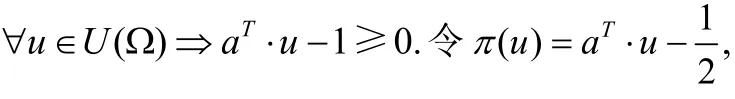
(i) ?u∈U(Ω)?π(u)=aT?u+k＞0且π(O)＜0;

(ii) ?u∈U(Ω)?π(u)=aT?u+k＜0且π(O)＞0.

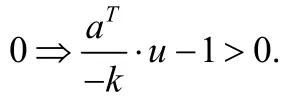
命題5將程序Q的秩函數計算問題與兩個點集(單點集{O}與像集U(Ω)的隔離問題建立了等價關系.下面的情形(II)表明,即便原點O?U(Ω),能嚴格分離單點集{O}與像集U(Ω)的超平面也未必存在.

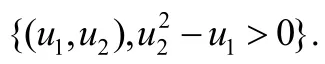
命題6.記號同上.U(Ω*)是?k中有界閉集.

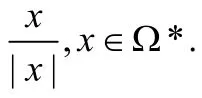
既然U(Ω*)=U(Ω*∩Θ),故有U(Ω*)是有界閉的.

如果O?U(Ω*),根據命題6,既然U(Ω*)是有界閉集,那么在O與像集U(Ω*)之間存在間隙,因而有可能在二者之間存在嚴格分離超平面.既然U(Ω)?U(Ω*),當O?U(Ω*)時,如果存在超平面π(u)能夠嚴格分離原點O與像集U(Ω*),那么π(u)也能嚴格分離原點O與U(Ω).類似于命題5的證明,我們有下列結論.

定理7.記號同上.假設U(x)在Ω*上有定義且原點O?U(Ω*)??k.如果存在超平面π(u)可將原點O與像集U(Ω*)嚴格分離,那么一定存在向量aT使得式(5)成立.

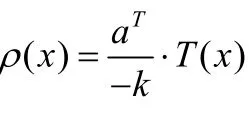
S1:從B集中取出有限個點記為B0?B.轉S2;

S2:調用SVM算法計算單點集A與有限點集B0的分離超平面,記為π(u)=aT·u+k.轉S3;

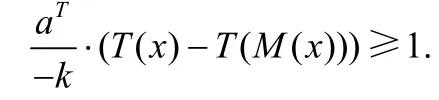
2.2 有限點集B0的構造

在上述的 S1中,需要從B=U(Ω*)中取出有限個點構成B0.由命題 8的證明可知,U(Ω*)=U(Ω*∩Θ).這里,Ω*∩Θ是一個有界閉集,Θ為單位球.因此,要構造B0,我們可以先從有界閉集Ω*∩Θ中取出有限點集C,然后通過U(x)映射得到點集U(C),從而得到B0=U(C).顯然,直接在球面Θ上通過打格點的方式取點并不方便.但單位球Θ總是可以被包含在某個超立方體Δ中.故,為了構造Ω*∩Θ上的點集C,我們采取如下思路:先在區域Ω*∩Δ上構造點集S.這里,Δ=[-m,m]n為一超立方體.然后對點集S中的點進行歸一化,得到歸一化后的點集S0.顯然,S0?Ω*∩Θ.最后令C:=So.而在超立方體Δ上打格子是相對容易的.因此,在區域Ω*∩Δ上構造點集S時我們可以通過對超立方體Δ打格子,然后將落入Ω*的格點收集起來構成點集S.圖2所示為一個算法化的取點過程.

在上述算法中,需要設置m的值.在我們的實驗中,m被取為100.此外,取點的間距h需要根據計算機的計算能力進行適當的調整,在計算機的實際計算能力范圍內,間距越小,取得的樣本點越多,最終計算出的代數分式函數經過驗證成為真正秩函數的可信度就越高.

2.3 例 子

本節將通過一個例子來闡述上文提出的方法.

例1:考慮下列循環:

該循環若使用 RegularChains[26]或者redlog[27]來求解線性或者非線性秩函數,均會因復雜度太高,而無法在有效的時間內得出結論.接下來將演示如何通過上文提出的基于SVM的方法來探測循環程序P1的代數分式秩函數.

(a) 首先將循環程序Q1進行齊次化處理,變成終止性等價的循環程序Q1′,如下所示:

若式(8)無解,則表明O?U(Ω*).由于代數分式以及根式的出現使得我們直接計算上述系統是否有解較為困難,因此,我們采取了一些化簡措施.比如,將上述系統中的代數分式化為多項式,利用平方手段消除根號等.由此我們得到下列多項式系統:

顯然,式(8)的任何一個解也必是式(9)的解.調用 Maple中的命令 solve計算可得式(9)僅有零解(0,0,0).顯然,(0,0,0)?Ω*.因為零解不可能是式(8)的解,故式(8)無解.這表明原點O?U(Ω*).

綜上所述,該循環程序滿足定理7的前提條件.因此,根據定理7,秩函數計算問題可歸結為O與U(Ω*)之間嚴格分離超平面的計算問題.

(b) 取樣本點.

采用第 2.2節介紹的取點算法,并將該算法中的參數m=100.在本例中我們令取點間距h=1.由于在約束條件中有x3≥0的條件,故x3不必從-100開始取點.通過取點算法,我們得到U(Ω*)中的有限點集B0=U(C).將B0中的點的標簽置為 1,而令單點集A=(O)的標簽為-1.接下來調用 SVM 算法計算A與B0的嚴格分離超平面π0(u)=aT·u+k.

(c) 使用LIBSVM軟件包計算出像空間中的劃分超平面.

本文采用MATLAB調用LIBSVM軟件包的方式來計算一個“硬分隔”的超平面.令=A∪B0.在求得劃分超平面之后,需要對中的點進行一次完整的測試,測試結果必須是 100%完全精確才能進行下一步操作.對該例通過計算得到劃分超平面中aT和k的值,

a=(2.798739925884132,-6.058645127373750,6.167554957795089),k=-1.000000000061875.

由上述計算得到的aT和k的值可確定一個嚴格分離超平面π0(u)=aT·u+k,它將A={O}與B0(?U(Ω*))嚴格分離.即:

(i) ?u∈B?π0(u)=aT?u+k＞0且π0(O)＜0;

(ii) ?u∈B?π0(u)=aT?u+k＜0且π0(O)＞0.

由類似于命題5的證明可知,無論哪種情形發生,都將有

接下來將驗證超平面π0(u)是否能將A={O}與B=U(Ω*)嚴格分離.為此,就需要驗證下列兩種情形之一是否成立.

(i) ?u∈U(Ω*)?π0(u)=aT?u+k＞0且π0(O)＜0;

(ii) ?u∈U(Ω*)?π0(u)=aT?u+k＜0且π0(O)＞0.

既然像點u∈U(Ω*)且由U(Ω*)的定義可知U(Ω*)={u∈?k:u=U(x),x∈Ω*},那么驗證上述(i),(ii)兩式就等價于驗證:

(i*) ?x∈Ω*?β(x)=aT[T(x)-T(M(x))]+k＞0且k<0;

(ii*) ?x∈Ω*?β(x)=aT[T(x)-T(M(x))]+k＜0且k>0.

這是因為,顯然地,若(i)(或(ii))成立,那么(i*)(或(ii*))也必成立.反之亦然.

(e) 使用BOTTEMA軟件包進行驗證.

既然k=-1.000000000061875<0,那么我們需要驗證:

是否成立.由于最終需要驗證式(5)或式(6)是否成立,所以,在本例中,我們直接驗證:

是否成立.BOTTEMA是一款強有力的不等式證明軟件.它可以驗證帶復雜根式的代數表達式的不等式是否成立.我們可以在Maple上調用BOTTEMA中的各類函數.通過驗證發現,

的確成立.故,

是該程序的代數分式型秩函數.因此循環程序是可終止的.

3 實 驗

下面給出基于SVM的多項式循環程序秩函數探測的具體算法.

實驗是在一臺裝有7.86GB的可用內存、處理器頻率為2.59GHz、操作系統64位的Windows操作系統的計算機上進行的.下面我們選取了4個循環程序用于對比.每個循環程序具體的計算方法可以參照前文中的例1.

針對表1中的6個循環程序,我們先后用量詞消去工具Redlog和Maple中的RegularChains軟件包來計算各自的線性秩函數,從表2可以看出,除了循環程序P4和P5外,其他5個循環程序都不能通過量詞消去方法來證明其是終止的.原因在于,量詞消去算法的復雜度太高,當循環程序的賦值語句或循環條件中含有非線性項時,無法在有效的時間內給出計算結果.在表2中,unknown表示計算時間超過10個小時仍未得出結果.Terminating表示相應的線性秩函數或代數分式秩函數被成功找到,故表明循環是終止的.特別地,在Terminating后面的括號中給出了計算秩函數所花費的時間.顯然,當循環中的表達式是線性時,基于量詞消去的工具即能有效地計算它們的線性秩函數.但,當表達式中含有非線性項時,實驗結果表明,量詞消去工具較難在可接受的時間內計算線性秩函數.此外,本文提出的基于SVM的方法所涉及的時間開銷包括:樣本點集的構造所需時間、SVM計算時間以及用 BOTTEMA驗證代數分式是否為秩函數所需時間.在實驗中我們發現,本文方法最主要的時間開銷在于樣本點集的構造.譬如,循環P3,樣本點集的構造花費了76分鐘.當然,我們也可以嘗試使用量詞消去的方法來合成非線性秩函數,但是,非線性項的引入同樣會帶來高復雜度的問題.從表 2中可以看出,本文提出的基于SVM的秩函數探測方法能夠探測出上述6個循環程序的確具有代數分式型秩函數,從而證明了這6個程序均是可終止的.上述6個循環程序在使用SVM的方法時,各自的取點間距h以及所產生的劃分超平面aT·u+k中的參數aT和參數k的計算值見表3.

Table 1 More examples表1 更多實例

從表3可以看出,循環程序P3和P4所采用的取點間距為0.5,而循環程序P2采用的取點間距為0.2.從理論上來說,取點間距越小,所選取的樣本點越多,最終計算出的代數分式函數被成功驗證為秩函數的可能性就越大.但是考慮到計算機的實際計算能力,針對不同的循環程序,取點間距要作適當的調整.

Table 3 The parameters generated using the SVM method表3 使用SVM的方法所產生的參數

4 總 結

本文提出了一種基于支持向量機(SVM)理論的求解單重無條件分支多項式循環程序秩函數的方法.該方法將秩函數計算問題歸結為二分類問題,然后利用SVM工具計算出一個候選的代數分式型函數,最后借助不等式自動驗證工具BOTTEMA對其進行驗證,以確定該代數分式型函數是否為循環程序的秩函數.由于SVM方法內部采用數值計算,因此相較于現有的基于量詞消去的秩函數計算方法,本文方法能在可接受時間內探測形式較為復雜的秩函數.實驗結果表明,針對某些循環程序,傳統的量詞消去方法不能在合理時間內判斷出它們是否有線性秩函數,但通過本文提出的方法卻可以找到其代數分式型秩函數.