稀疏度自適應分段正交匹配追蹤算法改進

李雪晴 丁佳靜 武雪姣

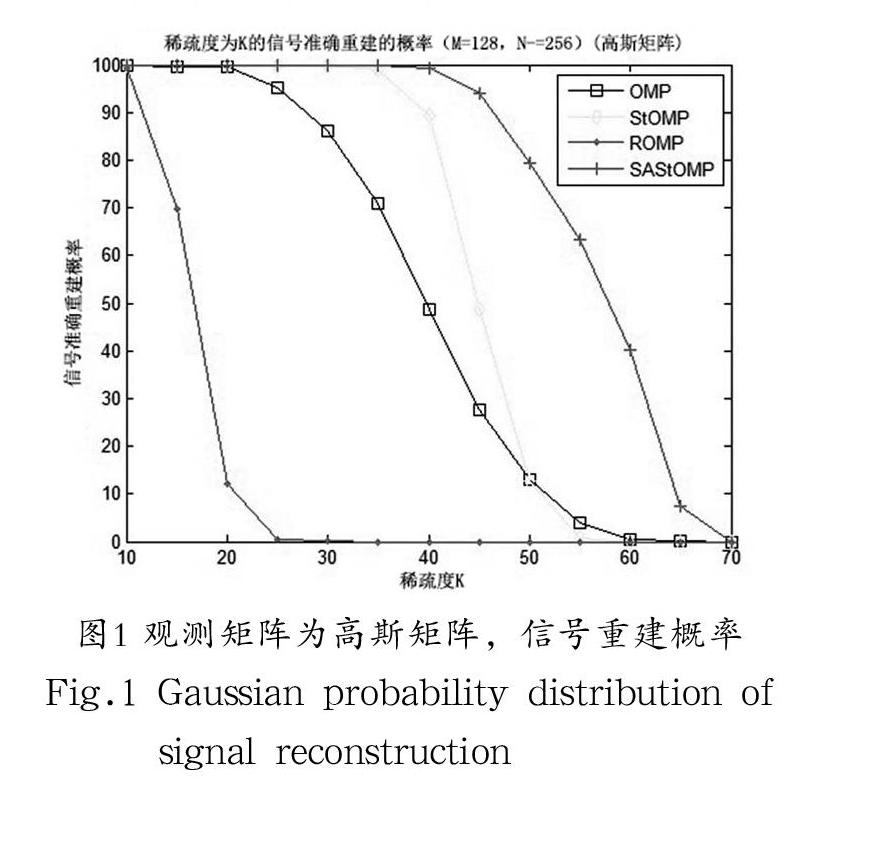
摘? 要：在基于壓縮感知的信號重構問題中，有一類常見情況——未知信號稀疏度。針對此類情況，提出稀疏度自適應分段正交匹配追蹤（Sparsity Adaptive Stagewise Orthogonal Matching Pursuit，SAStOMP）算法，該算法將自適應思想、變步長迭代思想與分段正交思想相結合，在未知信號稀疏度的情況下，自適應地選擇支撐集原子的個數，最終實現信號的精確重構。仿真結果表明，針對長度為256位的原始信號，該算法重建效果優于正交匹配追蹤算法、正則化正交匹配追蹤算法和分段正交匹配追蹤算法等。

關鍵詞：壓縮感知;信號重建算法;稀疏度自適應;分段正交匹配追蹤

中圖分類號：TP391? ? ?文獻標識碼：A

Abstract：Aiming at the reconstruction of unknown signal sparsity in compressed sensing，this paper proposes a new compression sensing signal reconstruction algorithm of SAStOMP （Sparsity Adaptive Stagewise Orthogonal Matching Pursuit）.The algorithm combines the ideas of self-adaptation，variable step size iteration and piecewise orthogonal design，in the case of unknown signal sparsity，selects adaptively the number of atoms of the support set ，finally realizes the accurate reconstruction of signals.Simulation results show that the proposed algorithm is superior to OMP，ROMP and StOMP for the original signals of 256 digits.

Keywords：compressed sensing;signal reconstruction algorithm;sparsity adaptive;stagewise orthogonal matching pursuit

1? ?引言（Introduction）

壓縮感知（Compressed Sensing，CS）技術之所以能夠利用較低維度的觀測值去重構較高維度的信號，在于充分利用了信號的稀疏性和可壓縮性[1]。研究CS理論，主要側重于三方面：信號的稀疏表示、觀測矩陣的設計，以及信號的重建算法。其中，信號重建算法是決定信號是否可以準確重構的關鍵步驟，其目的在于利用觀測值去高精度地重構真實值，當然觀測值的維度遠遠小于真實值。信號重構算法主要包括以下三類：組合優化類、凸優化類和貪婪迭代類[2]。貪婪迭代類算法往往運行速度較快，算法流程清晰。現有的貪婪迭代算法有匹配追蹤（Matching Pursuit，MP）[3]、正交匹配追蹤（Orthogonal Matching Pursuit，OMP）[4]、分段正交匹配追蹤（Stagewise Orthogonal Matching Pursuit，StOMP）[5]、正則化正交匹配追蹤（Regularized Orthogonal Matching Pursuit，ROMP）[6]、壓縮采樣匹配追蹤（Compressive Sampling Matching Pursuit，CoSaMP）[7]和子空間追蹤（Subspace Pursuit，SP）[8]。但是，貪婪迭代算法對待重構信號都有一個要求——稀疏度確定且已知，但事實上，真正的實際應用中，稀疏度通常不是先驗知識[9]。針對以上問題，本文在StOMP框架下，結合SAMP中稀疏度自適應的特點[10]，提出稀疏度自適應分段正交匹配追蹤算法（SAStOMP），該算法主要用于稀疏度未知情況下的信號重構。

2? ?壓縮感知理論（Compressed sensing）

在對信號進行重建時，能否運用壓縮感知理論在于確定該信號是否具有稀疏性，我們知道，每個一維信號，都可以用N×1維基向量線性表示。為了簡化問題，假設基向量為規范正交向量，使用N×N的基矩陣，信號x可以被表示為：

在該式中：S是投影系數構成的N×1維列向量。X是在時域或空間域的表示，Ψ為N×N維變換基，S是在Ψ域的表示。當信號可以僅被K個基向量線性表示時，則稱信號x為K-稀疏。作為壓縮感知理論的前提，稀疏性是實際很多信號不具有的，不能運用壓縮感知理論進行壓縮采樣，這會限制壓縮感知的發展。為了讓信號都具有這一性質，先對信號進行某種變換，使其具有稀疏性，之后就可對信號進行采樣壓縮和信號重構。設計一個與變換基不相關的觀測矩陣Φ，注意該矩陣的維度為M×N（M

上式中的Θ是恢復矩陣，維度為M×N。觀測矩陣Φ為已知矩陣，本文中分別取高斯隨機矩陣、伯努利矩陣、部分傅里葉矩陣為參考進行實驗分析。

3 稀疏度自適應分段正交匹配追蹤算法（Algorithm for sparsity adaptive stagewise orthogonal matching pursuit）

正交匹配追蹤算法是壓縮感知理論中較為經典的算法，算法簡單，重構效果尚可，但是這種算法每次只從觀測矩陣中選取1個最佳原子，即選取殘差最小的原子加入集合，這種算法重構準確度的增加是以犧牲迭代次數為代價的，當信號量激增時，整個重構的效率顯然會大大降低。接下來介紹StOMP算法，與OMP算法不同，StOMP算法在每次迭代中會選出多個原子，選取原子的個數是由提前設定的閾值決定的，之后在每次迭代中更新原子集合，最終找到最優解。顯然，StOMP算法的重構效率要比OMP算法高得多，下面介紹StOMP算法的流程與步驟[11]：

（1）初始殘差，計數器s=1。

（2）計算內積 。?

（3）可以通過設定軟閾值來產生相應集合，其中：為噪聲水平，為;θ為閾值參數，取值范圍為[2，3]。

（4）更新支撐集：，并利用最小二乘法計算支撐集上的逼近系數向量，。

（5）更新殘差（余量）。

（6）檢查終止條件：若s>10或者，（其中為誤差容限），算法終止并將作為最終輸出。否則，執行并轉到步驟（2） 。

StOMP算法每次迭代選取多個原子，大大提高了重構的效率，但該算法也存在以下不足之處：

（1）因為StOMP算法在每次迭代過程中，選擇的是根據閾值劃分出的原子集合，而不是最優原子，所以與OMP算法相比較，準確度大大降低。

（2）在上文中已經提到，選取原子的個數是由提前設定的閾值決定的，在實際應用中，閾值往往不太容易確定。

（3）無論是OMP算法還是StOMP算法，都需要確定待重構信號的稀疏性，但在實際的應用中，不同來源的信號的稀疏度往往是未知的且很難確定。

考慮到OMP算法和StOMP算法的優缺點，本文結合SAMP算法[12]的自適應思想，提出一種改進的稀疏度自適應的壓縮感知算法。改進的算法無須明確待重構信號的稀疏度，而是在迭代過程中一步步去逼近真實的稀疏度K，最終實現信號重構。算法流程如下[12，13]：

輸入：M×N的傳感矩陣A=ΦΨ;N×1維觀測向量y;迭代次數S，默認為10;門限參數ts，默認為2.5;步長ST。

輸出：信號稀疏表示系數估計;殘差。

（1）初始化：，，，，。

（2）計算（即計算，1≤j≤N），選擇u中L個最大值，將這些值對應A的列序號j構成集合（列序號集合），選擇u中大于門限的值，將這些值對應A的列序號j構成集合（列序號集合）。

（3）令，;若（即無新列被選中），則停止迭代進入第（8）步。

（4）求的最小二乘解：。

（5）從中選出絕對值最大的L項記為，對應的的L列記為，對應的A的列序號記為，記集合。

（6）更新上一步驟所得殘差，使得。

（7）如果則停止迭代進入第（8）步;如果，則更新步長L=L+ST，返回第（2）步繼續進行迭代;否則，如果t≤S停止迭代進入第（8）步，否則返回第（2）步繼續迭代。

（8）重構所得在處有非零項，其值分別為最后一次迭代所得。

綜上，SAStOMP算法將分階段正交化思想，以及自適應思想相結合，在提高重構效率的同時保證了信號重構的準確度。

4 實驗結果及分析（Experimental results and analysis）

為了檢驗本文算法的正確性和有效性，將本文改進的算法與OMP算法、ROMP算法，以及StOMP算法進行比較。本文涉及的實驗在華碩Y481C筆記本（4GB DDR3內存，i7-3573）上，通過MATLAB R2014a仿真完成。當觀測矩陣為高斯隨機矩陣、伯努利矩陣和部分傅立葉矩陣時，信號準確重建概率分別如圖1、圖2、圖3所示。

從圖1可以看出，當信號長度為256位，觀測值集合為128位，觀測矩陣為高斯矩陣時，改進的SAStOMP算法明顯優于OMP算法、ROMP算法、StOMP算法。當稀疏度接近45時，OMP算法和StOMP算法信號準確重構的概率急劇下降，改進的SAStOMP算法仍能100%精確重構信號。當稀疏度接近55時，OMP算法和StOMP算法幾乎不能重構信號，而改進的SAStOMP算法性能良好，準確重構信號的概率接近65%。

從圖2可以看出，當信號長度為256位，觀測值集合為128位，觀測矩陣為伯努利矩陣時，改進的SAStOMP算法依然明顯優于OMP算法、ROMP算法、StOMP算法。隨著稀疏度不斷增加，信號精確重構概率基本趨勢與觀測矩陣為高斯矩陣的情況相同。

從圖3可以看出，當信號長度為256位，觀測值集合為128位，觀測矩陣為傅立葉矩陣時，改進的SAStOMP算法僅次于經典的OMP算法，明顯優于ROMP算法和StOMP算法。

經過仿真實驗和上述實驗結果分析，綜合來說，本文提出的算法不需要信號稀疏度作為先驗知識，表現出的性能整體優于經典的OMP算法、ROMP算法和StOMP算法，具有良好的實用價值。

5? ?結論（Conclusion）

本文提出了SAStOMP算法，該算法不需要稀疏度K作為先驗知識，彌補了貪婪迭代類算法的最大不足。MATLAB實驗仿真結果表明，改進的SAStOMP算法優于OMP、ROMP和StOMP算法，提高了信號稀疏度較大時重構信號的準確度。

參考文獻（References）

[1] Zhou C，Gu Y，Zhang Y D，et al.Compressive sensing-based coprime array direction-of-arrival estimation[J].Iet Communications，2017，11（11）：1719-1724.

[2] 唐朝偉，王雪鋒，杜永光.一種稀疏度自適應分段正交匹配追蹤算法[J].中南大學學報（自然科學版），2016，47（3）：784-792.

[3] Chen C H，Tsai C R，Liu Y H，et al.Compressive Sensing （CS） Assisted Low-Complexity Beamspace Hybrid Precoding for Millimeter-Wave MIMO Systems[J].IEEE Transactions on Signal Processing，2017，65（6）：1412-1424.

[4] Nouasria H，Et-Tolba M.Sensing matrix based on Kasami codes for compressive sensing[J].IET Signal Processing，2018，12（8）：1064-1072.

[5] Donoho D L，Tsaig Y，Drori I，et al.Sparse Solution of Underdetermined Systems of Linear Equations by Stagewise Orthogonal Matching Pursuit[J].IEEE Transactions on Information Theory，2012，58（2）：1094-1121.

[6] Needell D，Vershynin R.Signal Recovery From Incomplete and Inaccurate Measurements Via Regularized Orthogonal Matching Pursuit[J].IEEE Journal of Selected Topics in Signal Processing，2010，4（2）：310-316.

[7] Needell D，Tropp J A.Tropp，J.A.：CoSaMP：iterative signal recovery from incomplete and inaccurate samples[J].Applied & Computational Harmonic Analysis，2008，26（3）：301-321.

[8] Dai W，Milenkovic O.Subspace Pursuit for Compressive Sensing Signal Reconstruction[J].IEEE Transactions on Information Theory，2009，55（5）：2230-2249.

[9] 吳迪，王奎民，趙玉新，等.分段正則化正交匹配追蹤算法[J].光學精密工程，2014，22（5）：1395-1402.

[10] sfs DO T T，GAN L，NGUYEN N，et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C].Proceedings of the Asilomar Conference on Signals，Systems and Computers.Pacific Grove，CA：IEEE Computer Society，2008：581-587.

[11] onoho D L，Tsaig Y，DroriI，Starck J L.Sparsesolution of underdetermined linear equations by stagewise orthogonal matchingpursuit[J].IEEE Transactions on InformationTheory，2012，58（2）：1094-1121.

[12] Thong T.Do，Lu Gan，NamNguyen，et al.Sparsityadaptive matching pursuit algorithm for practical compressed sensing[C].AsilomarConference on Signals，Systems，andComputers，Pacific Grove，California，2008，10：581-587.

[13] 楊成，馮巍，馮輝，等.一種壓縮采樣中的稀疏度自適應子空間追蹤算法[J].電子學報，2010，38（8）：1914-1917.