火箭大偏航入軌雙回路擾動觀測補償有限時間收斂滑模控制

吳燕生

(中國航天科技集團有限公司,北京100048)

0 引言

未來空間運輸和空間應急救援等快速響應任務對火箭大偏航控制方法提出了特殊要求,以末級火箭異面機動變軌為例,相對于多次軌道面調整,一次性異面機動變軌極大地提高了時間效率,而大偏航角姿態控制對于實現一次性異面機動變軌至關重要。經典PID火箭姿態穩定控制方法具有在線計算量小、易于工程實現的優點,因此得到廣泛應用。然而,考慮到大偏航角飛行條件下姿態角與角速度為非線性關系,以及存在質量、轉動慣量、推力等參數不確定,經典控制方法往往難以保證良好的動態過程和穩態特性,基于標稱狀態特征點設計的控制參數在參數不確定情況下收斂特性難以證明。因此需要設計自適應、強抗擾的運載火箭姿態控制系統,以滿足大偏航角飛行條件下姿態跟蹤控制需求。

為解決對有外界擾動和不確定參數的運載火箭高精度姿態控制問題,錢默抒等[1]提出了一種基于雙冪次滑模的變結構姿態控制算法,利用觀測器實現對不可測彈道傾角的高精度估計和對包含參數不確定在內的復合擾動的高精度觀測補償。于亞男等[2]基于自抗擾理論和分數階控制提出了一種運載火箭抗干擾分數階控制器,通過設計擴張狀態觀測器對系統的內部和外部干擾進行估計,實現了高精度控制。王曄等[3]為抑制運載火箭自身結構參數變化和內外擾動對姿態控制精度和姿態穩定性的影響,設計了自抗擾控制器。通過跟蹤微分器、擴張狀態觀測器以及姿態反饋控制器,獲取了良好的動態性能、抗擾性和較強的魯棒性。自適應滑模控制方法和魯棒H∞控制方法也在文獻[4-5]中分別被提出以增強火箭控制系統對參數不確定的適應性。朱海洋等[6]提出了一種基于徑向基神經網絡和低通濾波器的滑模控制方法,以解決液體運載火箭飛行過程中參數時變性和各種不確定性問題。陳書釗等[7]將狀態預測神經網絡控制應用于小型可回收火箭。潘豪等[8]為解決新型中型運載火箭飛經大風區的氣動過載不穩定問題,采用主動減載控制設計,分析了基于擴張狀態觀測器的自適應減載控制方法。Li等[9]將小型固體測試火箭的不匹配干擾視為輸入通道中的“總干擾”進行補償建立EID系統,按照傳統的頻域方法,提出了一種基于H∞和等效輸入擾動以增強系統抗干擾性的三軸姿態控制器。Bayat等[10]針對導彈的干擾不匹配、動力學未建模等問題,提出了一種固定時間自適應模型參考滑模控制方法,利用導彈狀態方程和模型參考狀態方程的跟蹤誤差,建立了滑模曲面,并將不匹配擾動和未建模的動力學問題作為狀態方程的模型誤差進行處理。

盡管文獻[2-10]的研究成果能有效提高了控制系統對參數不確定的適應性,但是文獻中考慮的姿態角環與角速度環均為線性關系;在大偏航角情況下,火箭的俯仰、偏航、滾轉三通道姿態運動學方程存在耦合,即三通道姿態角和角速度間不再是簡單的線性關系,姿態環的非線性項為姿態控制系統引入了非匹配擾動項,上述控制方法在設計過程中均沒有考慮非線性關系下的非匹配擾動項影響,因此難以保證大偏航飛行過程中的姿態控制性能。

基于此,提出火箭大偏航入軌雙回路擾動觀測補償有限時間收斂滑模控制,通過“雙回路+虛擬控制量”方式將控制模型中非匹配擾動項轉化為匹配擾動項,基于有限時間收斂擾動觀測器實現對內外回路擾動的高精度觀測補償,并通過有限時間收斂滑模控制器實現控制誤差的有限時間收斂。相較于經典PID控制,該方法具有強適應性和抗擾性,能夠有效應對參數不確定下系統特性變化;相較于現有的運載火箭自適應控制方法,該方法能夠有效解決大偏航角條件下三通道的姿態運動耦合帶來的非線性模型特性,保證了大偏航角條件下三通道姿態角指令高品質跟蹤。

本文第一節對大氣層外火箭姿態運動學和動力學進行建模,并推導面向控制的姿態模型,為后續控制系統構建奠定基礎;第二節給出雙回路擾動觀測補償有限時間收斂滑模控制系統框架,并引入有限時間收斂擾動觀測器和有限時間收斂滑模控制器,基于Lyapunov第二法對閉環控制系統有限時間收斂特性進行證明;第三節對比經典PID控制和雙回路擾動觀測補償有限時間收斂滑模控制方法,充分驗證雙回路控制方法的抗擾性、高精度和良好的動態性能。

1 火箭大偏航入軌控制模型構建

1.1 姿態運動學和動力學建模

考慮火箭具有“十”字型布局的四臺單擺發動機,發動機的安裝示意圖如圖1所示。

圖1 四臺單擺發動機安裝示意圖Fig.1 Schematic diagram of four single-track engines

圖1中,箭頭方向為各發動機擺動的正方向,且4臺發動機理論推力大小相同,設定為P。三通道發動機控制力矩表達式為

其中,r c為發動機安裝半徑,x R為推力作用點距箭體理論尖點的距離,x g為火箭質心距箭體理論尖點的距離。δγ、δψ和δφ分別表示滾轉、偏航和俯仰三通道發動機等效擺角。等效擺角和各臺發動機實際物理擺角關系為

考慮運載火箭體軸均為慣性主軸,則火箭入軌段姿態運動學和動力學微分方程表述為

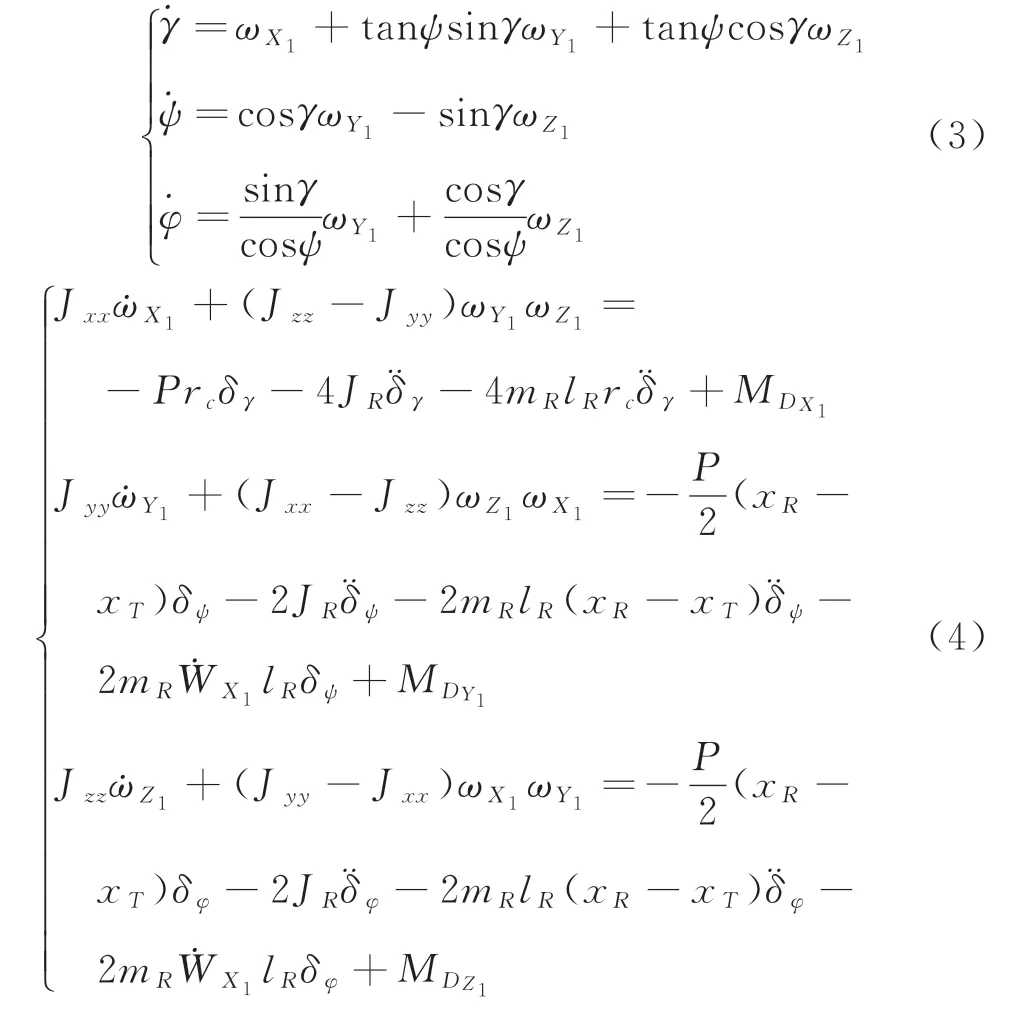
其中,ωX1、ωY1、ωZ1分別表示滾轉角速度、偏航角速度和俯仰角速度,φ、ψ、γ分別表示俯仰角、偏航角和滾轉角,J xx、J yy、J zz分別表示三體軸轉動慣量,J R表示發動機擺動慣量,m R表示發動機擺動質量,l R表示發動機質心到擺軸的距離,表示火箭縱向視加速度,M D X1、M DY1、M DZ1分別表示由于結構干擾引起的干擾力矩,分別表示發動機三通道等效擺角擺動加速度。

1.2 面向控制的姿態模型構建

建立面向控制的三通道姿態模型如下

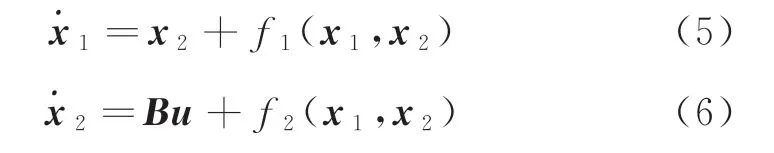
其中,狀態量x1和x2分別為

控制矩陣B為

系統擾動項f1(x1,x2)和f2(x1,x2)為

由式(9)可見,當火箭以大偏航角姿態飛行時,火箭三通道姿態運動學均存在耦合,即此時姿態環和姿態角速度環不再是簡單的線性積分關系。

由此可見,由于擾動項f1(x1,x2)和f2(x1,x2)同時存在,因此實際模型中,同時存在有匹配擾動項f2(x1,x2)和非匹配擾動項f1(x1,x2),需展開控制系統設計,以實現在匹配/非匹配擾動共同存在下姿態指令高精度快速跟蹤。

2 雙回路擾動觀測補償有限時間收斂滑模控制

2.1 數學準備

定義1(有限時間穩定性)針對系統=f(x),x∈R n,原點是有限時間穩定,如果原點附近存在一個非空鄰域{0}∈D?R n,則:(i)系統在原點及其鄰域D/{0}是李雅普諾夫(Lyapunov)狀態下穩定的;(ii)存在一個沉淀時間函數T:D/{0}→R+使系統有唯一解W x0(t),在t∈[t(0),T(x0)]和x0=x(t0)∈D/{0}條件下滿足

引理1假設V(x):R n→R是一個連續的正定函數,在原點開鄰域D?R n內滿足如下微分不等式

其中,μ是正系數,η是正奇數且滿足0＜η＜1。則函數V滿足如下不等式

2.2 控制系統構建

為實現對中匹配/非匹配擾動項的高精度觀測補償,考慮采用雙回路形式,結構框圖如圖2所示。

圖2 火箭大偏航入軌雙回路擾動觀測補償有限時間收斂滑模控制結構框圖Fig.2 Structure of observer-based finite-time convergence sliding mode control system for rocket orbital insertion with large yaw

如圖2所示,大偏航飛行條件下運載火箭姿態控制系統分解為姿態角指令跟蹤環和角速度控制環。姿態角指令跟蹤環輸出角速度指令作為虛擬控制量傳遞給角速度控制環,角速度控制環跟蹤傳遞來的虛擬控制量,通過雙回路指令跟蹤控制,實現角度指令的快速精確響應。

需要指出的是,由于引入了虛擬控制量,因此此時姿態環的控制量為ωc,即角速度指令,則擾動項f1(x1,x2)已由非匹配擾動項變為匹配擾動項,可通過擾動觀測器進行精確觀測補償。

考慮外部姿態角指令為X c

則姿態環角度指令跟蹤誤差方程為

其中,為姿態角指令變化率,為實際姿態角變化速率

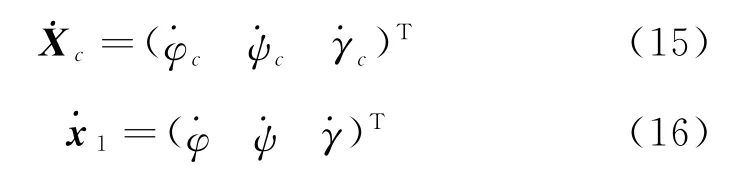
將x2描述為X2c,則

同樣,角速度環跟蹤誤差方程為

其中,角速度指令變化率為

實際角速率微分為2

微分器1用于輸出,微分器2用于輸出;擾動觀測器1用于補償1(x1,x2),擾動觀測器2用于觀測補償2(x1,x2)項。

滑模控制器1、2的設計目的則是實現如下系統的穩定控制

其中,、分別表示擾動觀測器1、2觀測收斂動態過程中的觀測誤差,且滿足

需要指出的是,、范數存在上確界是合理的,因為火箭在大偏航入軌過程中無大氣,且觀測器收斂存在動態過程,因此觀測器的觀測值和實際值均不會產生突變,則觀測誤差的導數項范數存在上確界。

下面分別給出系統各組成部分——微分器、擾動觀測器及滑模控制器的設計形式。

2.2.1 有限時間收斂微分器/擾動觀測器

引入定理1如下所示。

定理1[11]考慮存在系統

分別設計觀測器1、2

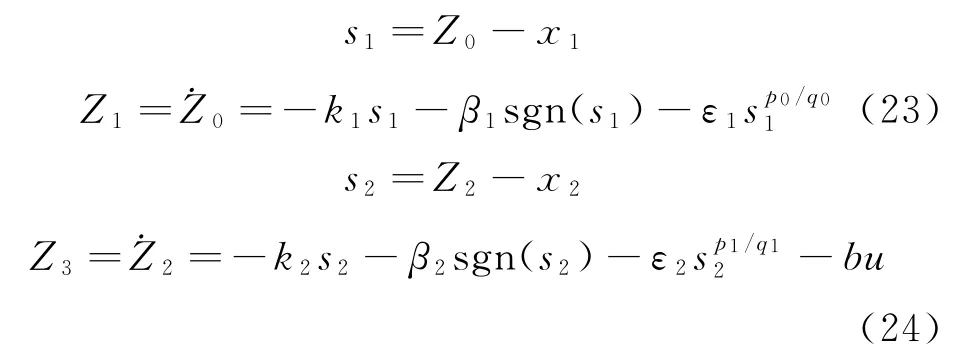
其中,sgn(·)表示符號函數,k1、k2、β1、β2、ε1和ε2為正系數,p0、q0、p1、q1為正奇數且

則可利用Z1實現對的有限時間收斂觀測,利用Z3實現對的有限時間收斂觀測。

證明:構造雙李雅普諾夫函數為

則求導得到

根據引理1可知,觀測器1、2均能實現有限時間收斂。

引用定理1,則微分器1、2形式分別為

其中,z0∈R3、z2∈R3分別用于觀測e1、e2;k1、k2、β1、β2、ε1和ε2均為對角陣形式的參數設計矩陣,sgn_f(s1)為

其中,s11、s12和s13為s1的分量,sgn_f(s2)的形式與之相同。

微分器1、2收斂時間為

綜上可知,擾動觀測器1、2形式可表達為

則擾動觀測器輸出的補償控制項分別為

2.2.2 有限收斂滑模控制器

設計雙回路非奇異終端快速滑模面為[12]

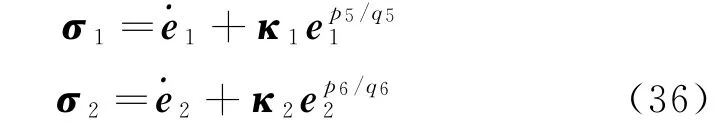
其中,κ1＞0,κ2＞0,p5＞q5,p6＞q6且均為正奇 數,σ1=(σ11σ12σ13)T,σ2=(σ21σ22σ23)T。

根據文獻[12]進行推導,可給出定理2如下。

定理2針對系統,若

其中

存在

在式(37)、式(38)作用下,式(21)能夠在有限時間內收斂至滑模面式(36),且收斂時間滿足

證明:由式(36)可得

將式(21)代入式(43)可得

給出如下假設:、滿足

其中

需要說明的是,由于、范數存在上確界,因此必然存在對角陣ρ1、ρ2,使得式(46)、式(47)成立。

由文獻[12]可知,當v1、v2符合式(39)、式(40)時,系統在有限時間內收斂至滑模面上,且收斂時間為式(42)。

現有文獻中對快速終端滑模面上滑動模態的收斂性證明較多,因此在本文中不作展開,具體過程可參考文獻[12]。

3 仿真驗證

3.1 仿真參數設置

仿真中采用的運載火箭總體參數如表1所示。

表1 仿真參數Tab.1 Simulation parameters

仿真中雙回路擾動觀測滑模控制參數為

為充分驗證雙回路擾動觀測補償滑模控制的優良性能,引入經典PID控制方法進行對比。三通道PID控制參數均設計為

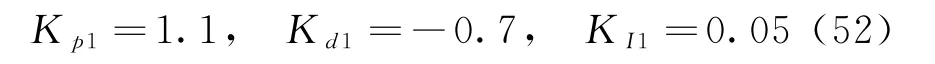
3.2 仿真結果及分析

俯仰、偏航、滾轉通道初始姿態角如式(53)所示

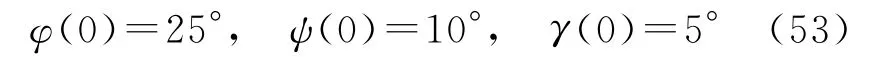
設定俯仰、偏航通道存在10°階躍響應指令,且滾轉通道需要恢復至0°,則三通道響應曲線如圖3～圖5所示。

由三通道姿態角響應隨時間變化曲線可知,PID方法作用下三通道上升時間均超過3s,而雙回路滑模方法作用下俯仰角/偏航角/滾轉角上升時間小于2s;同時,雙回路滑模方法控制下三通道姿態角穩態誤差小于0.1°,顯著小于PID方法作用下的穩態誤差,顯示出雙回路滑模控制方法的響應快速性和高穩態精度。

圖3 時間-滾轉角變化曲線Fig.3 Time history of roll angle

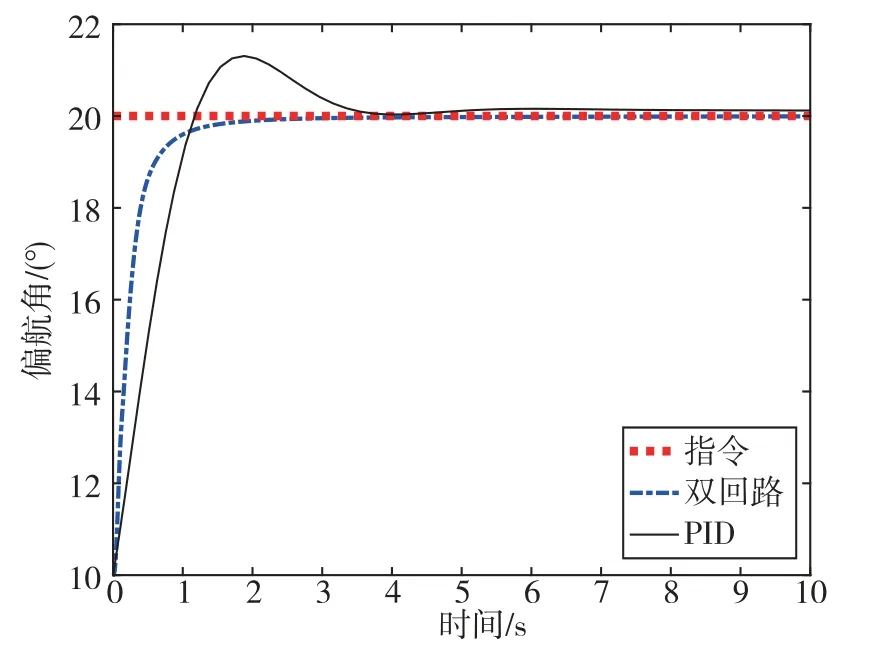
圖4 時間-偏航角變化曲線Fig.4 Time history of yaw angle

圖5 時間-俯仰角變化曲線Fig.5 Time history of pitch angle

為驗證雙回路滑模控制系統強抗不確定性和擾動性,考慮引入由結構偏差引起的擾動項為

參數不確定設定為:推力偏差+2%,J yy(J zz)偏差+20%,J xx偏差+20%,x R偏差-10%,x t偏差+10%。則仿真曲線如圖6～圖8所示。

圖6 時間-滾轉角變化曲線Fig.6 Time history of roll angle

圖7 時間-偏航角變化曲線Fig.7 Time history of yaw angle

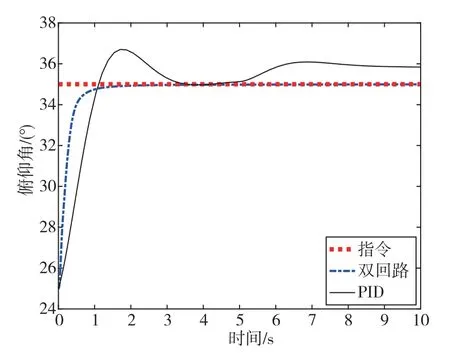
圖8 時間-俯仰角變化曲線Fig.8 Time history of pitch angle

對比圖6～圖8可知,當第5s突然施加結構偏差引起大擾動時,PID作用下火箭姿態控制系統無法實現快速適應及偏差收斂,而雙回路滑模控制作用下三通道姿態角響應曲線無明顯變化,充分顯示了雙回路滑模控制方法的強抗擾性和抗參數不確定性。

4 結論

為解決大參數不確定和擾動下大偏航入軌火箭姿態控制問題,本文提出了一種雙回路擾動觀測補償有限時間收斂滑模控制方法,通過“雙回路+虛擬控制量+擾動觀測器”方式有效觀測并補償了匹配/非匹配擾動項,基于有限時間收斂滑模觀測器實現了誤差的快速高精度收斂,結合“微分器+擾動觀測器+滑模觀測器”,實現了在大參數不確定和干擾條件下火箭姿態指令的有限時間快速高精度跟蹤。仿真結果表明,雙回路滑模控制方法具備有良好的動態過程和高穩態精度,對參數不確定和外部干擾具有強適應性。