逐步判別分析方法在新北油田水淹層識別中的應用

馬福軍，李 楠，劉 剛，王 婷

(中國石油吉林油田分公司，吉林 松原 138000)

新北油田區域構造位于松遼盆地中央坳陷區扶余華字井階地的扶余-新立背斜構造北翼，是一個高滲透、被斷層復雜化的構造巖性油藏，1978年以425 m反九點法面積注水方式全面投入開發，開發目的層為黑帝廟油層。1994年加密調整成300 m反九點法面積注水井網，2001年再次加密調整成212 m反九點法面積注水井網，現已進入高含水期開發階段。隨著油田水驅開發程度的不斷提高，油田的水淹程度日趨增高，導致油層的流體性質、孔隙結構、巖石的物理化學性質以及油氣水分布規律等都會發生一定程度的變化[1-7]，使得調整井水淹層解釋相對復雜化，解釋結果與實際符合率相對較低。尤其在近幾年，老區調整新井投產后的實際水淹情況與測井解釋結果相差較大，統計2015年完鉆投產井實際含水與測井解釋符合程度為75.4%，嚴重影響了產能形象。水淹層識別研究是油田開發后期開發調整的關鍵，近幾年測井技術人員也相應開展了水淹層機理方面的研究，但仍沒有突破性進展，因此，我們在分析油層水淹對測井響應產生的主要變化基礎上，采用逐步判別分析方法來識別水淹層，提高水淹層識別與實際的符合程度,為油田開發后期調整井水淹層的識別提供新的思路和方法。

1 逐步判別分析的基本原理

判別分析是判別樣品所屬類型的一種統計方法[8-12]，其主要思想就是用統計方法將待判樣品與已知樣品進行類比，確定待判樣品歸屬于那一類。實際往往常用的是多組線性判別方法，考慮盡可能多的變量來區分總體，但每個變量所攜帶的地質信息不同，對區分總體判別的貢獻不一樣，為此采用逐步判別方法，變量有進有出，每一步都對變量貢獻進行檢驗，在把一個重要變量引入判別函數后，同時考慮到較早引入判別函數的某些變量隨著新變量的引入而變得不重要，將其從判別函數中剔除,最終保留有“重要性”的變量，使判別函數更加簡潔實用。 其計算步驟如下：

設有m個總體，第g總體有ng個樣品，每個樣品均觀測了p項指標，原始數據記為：

Xgjk(g=1,2……,m;j=1,2,……,ng;k=1,2……,p)

(1)

式中：Xgjk表示第g組第j個樣品的第k項指標。

首先計算出各組變量均值Xgk和總均值Xk，組內離差矩陣W與總離差矩陣T。

1.1逐步篩選變量

用Wilks統計量U來檢驗p個變量區分m個總體的能力。U是矩陣W與矩陣T行列式值之比。

1.1.1引入變量

按式(2)對未引入的變量Xi計算判別能力Ui,選出判別能力最大的變量Xr，并按式(3)計算出F1，若F1>Fa(m-1,N-m-l),則Xr引入判別式。

Ui=Wii/Tii

(2)

式中：Ui是第i個變量的判別能力；Wii是組內離差矩陣i行i列元素；Tii總離差矩陣i行i列元素。

(3)

式中：F1是引入變量的F檢驗值；l是判別式已引入的變量數，N是m個總體全部樣品總數(N=n1+n2…+ng)。

1.1.2剔除變量

按式(4)對已引入的變量Xj計算判別能力Uj,選出判別能力最小的變量Xr,并按式(5)計算出F2，若F2≤Fa(m-1,N-m-l+1)，則Xr判別力不顯著，從式中剔除。

Uj=Tjj/Wjj

(4)

式中：Uj是第j個變量的判別能力；Wjj組內離差矩陣j行j列元素；Tjj總離差矩陣j行j列元素。

(5)

式中：F2是剔除變量的F檢驗值。

每引入或剔除一個變量都要對矩陣W與T進行一次求解求逆并行變換[7]，重復式(2)～(5)計算步驟，直到沒有變量可以剔除，也沒有變量可以引入為止，篩選變量完成。

1.2計算判別函數

篩選變量結束后，方程最終已引入了D個變量，可算得各組判別函數如下：

(6)

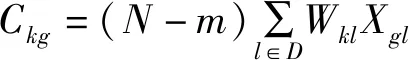
式中，Ckg為判別函數的系數；Cog為判別式中常數項；D為方程最終引入的變量個數。

1.3分組判別

設一樣品為X=(x1,x2，……，xp)，將它代入式(6)算出m個判別函數值。

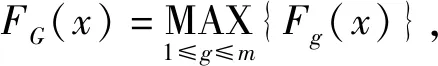
2 判別分析方法在水淹層識別中的應用

油層水淹級別劃分是按含水百分數大小劃分，按標準分為5個級別，見表1。

表1 油層水淹級別劃分標準

地質工程師通過多年來對水淹層識別方法的研究[13-16]，認為油層水淹后在測井響應引起變化的主要指標有：0.5 m電阻率、聲波時差、自然伽馬、孔隙度、滲透率和含油飽和度。

為此，我們選擇這6項測井參數作為逐步判別的指標變量，建立判別函數。

2.1 逐步判別分析判別函數的建立

收集新北油田2015年完鉆投產的30口井生產數據。

由于注水開發時間較長，老區不存在未水淹層，因此只建立弱水淹層、中水淹層、強水淹層和特強水淹層4個級別的判別函數，其數據見表2。

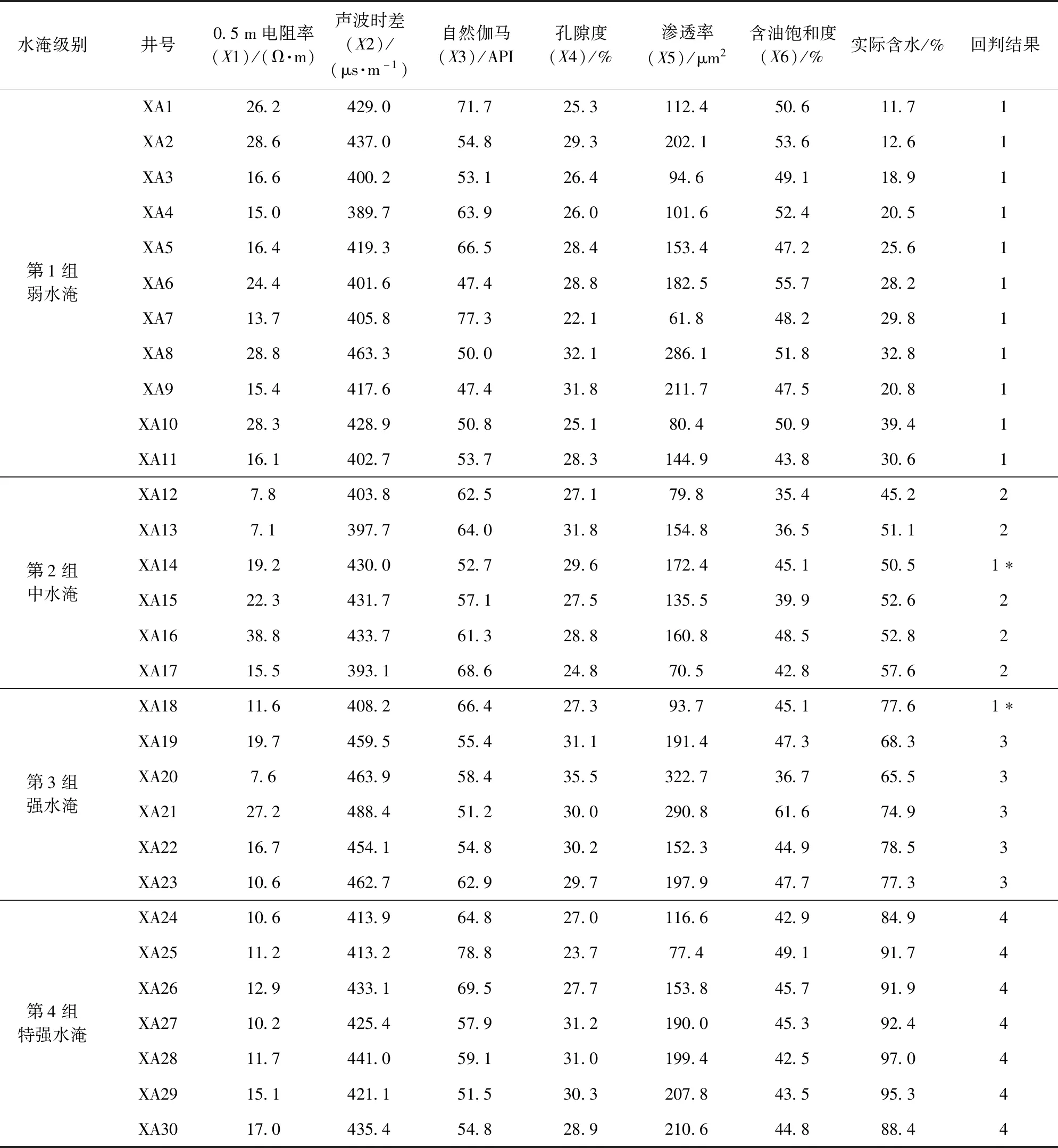
表2 新北油田30口井各項指標與水淹級別數據

注：回判結果：1.弱水淹；2.中水淹；3.強水淹；4.特強水淹；*.與實際不符。

用表2中X1～X6的6列數據，按式(1)構成4個總體6個指標數據，經式(2)～(6)計算，最終有3個變量引入判別函數，分別是0.5 m電阻率、聲波時差和含油飽和度。其4個總體的判別函數如下：

第1組:F1(x)=-443.694 5-4.957 8x1+1.778 1x2+4.913 6x6

第2組:F2(x)=-411.204 8-4.657 3x1+1.758x2+4.243 5x6

第3組:F3(x)=-529.860 5-5.468 2x1+1.980 8x2+5.043 1x6

第4組:F4(x)=-475.674 9-5.248 5x1+1.869 9x2+4.864x6

式中：x1是0.5 m電阻率，Ω·m；x2是聲波時差，μs/m；x6是含油飽和度，%。

2.2 逐步判別分析判別函數的顯著性檢驗

逐步判別分析建立的判別函數使各總體間差異最大，總體內差異最小，所建的判別模型需驗證顯著性，通常有兩種方法：一是回判率檢驗，二是總體間顯著性檢驗。

2.2.1 回判率檢驗

為了驗證所建判別函數的顯著性，將原始樣品代入所建判別函數中進行回判，一般認為，回判正確率大于75%，判別函數有效[8，17]。經原始樣品數據代回判別式，其回判結果見表2，中水淹層判錯1口，強水淹層判錯1口，弱水淹層和特強水淹層全部判對，總體看30口井判對28口井，回判正確率為93.3%，所建立的判別函數可應用于實際水淹層識別。

2.2.2 總體間顯著性檢驗

把總體兩兩配對逐次檢驗兩總體間的顯著性，用馬氏距離構成的統計量[12，17]Fef來檢驗，通過計算兩兩總體間馬氏距離和統計量Fef檢驗值(見表3)，總體內兩類間的Fef值均大于Fa(a=0.1)的值。檢驗效果顯著，判別函數可有效區分兩兩總體，所建模型可靠。

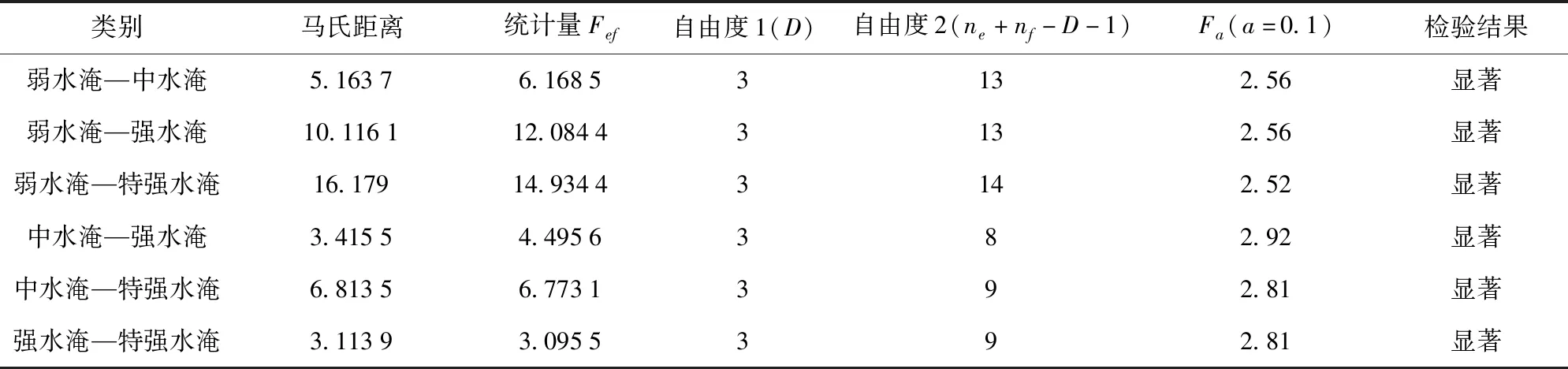
表3 4個總體兩兩分類間判別效果檢驗

2.3 判別函數的實際應用

2.3.1 應用實例

應用所建立的判別函數對2018年完鉆的12口井進行水淹層識別，結果見表4，與試油生產實際數據對比，其中1口井XB10實際是中水淹，判別函數識別成弱水淹了，其余11口判別函數識別結果與實際相符，說明所建的判別函數符合實際。

2.3.2 逐步判別方法與測井解釋方法效果對比

從這12口井測井解釋結果與實際對比看，其中4口井與實際含水不相符，測井解釋結果符合率為66.7%,逐步判別方法符合率為91.7%，遠高于測井解釋的符合率。圖1是XB9井新舊方法解釋成果對比，測井解釋結果是中水淹，試油結果是強水淹，逐步判別結果是強水淹，可以看出逐步判別方法識別水淹層與測井解釋結果對比具有較高的識別精度。

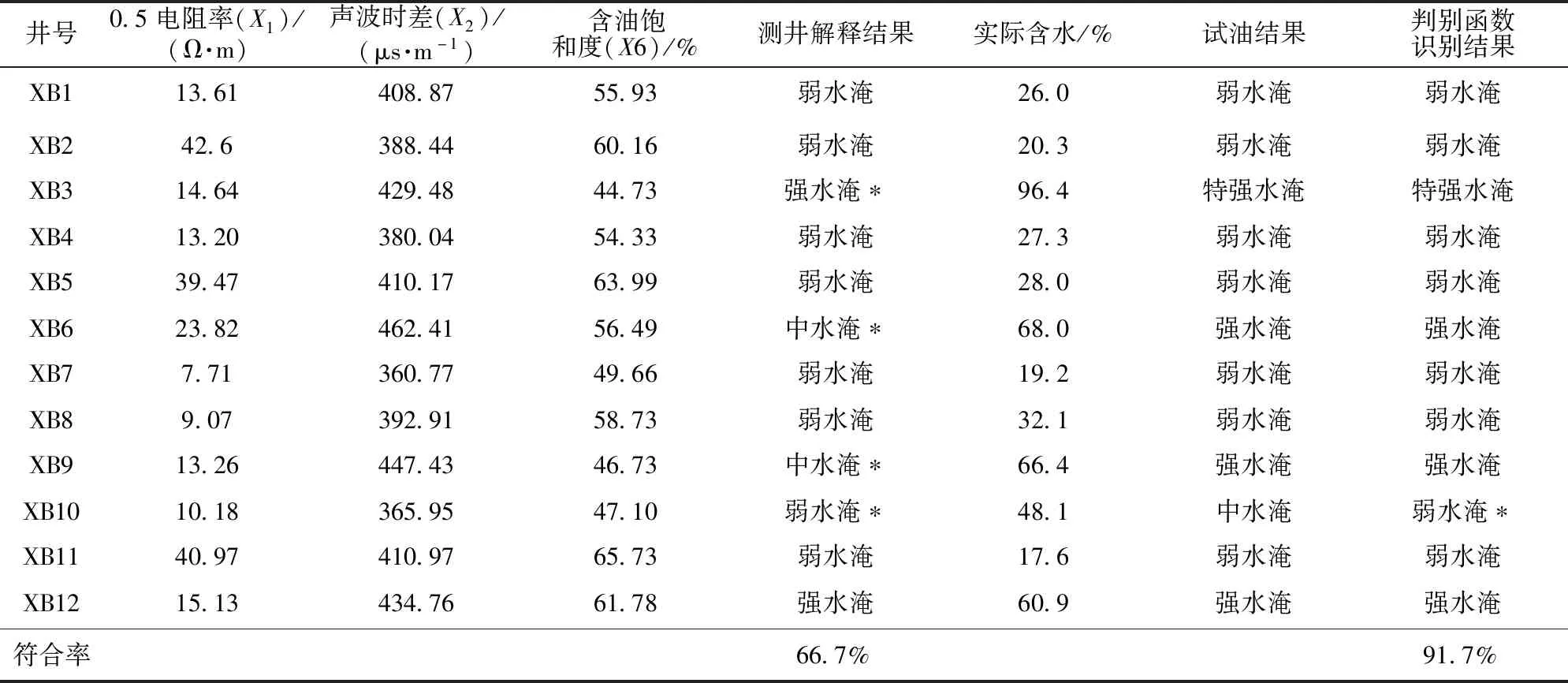
表4 新北油田2018年12口調整井水淹級別識別情況

注：*與實際不符。

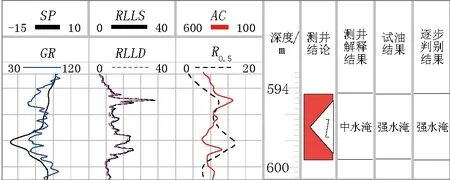
圖1 XB9井測井解釋與判別分析成果對比

2.4 誤差分析

分析造成誤差的原因主要有兩個方面：一是影響油層水淹的因素較多，每個因素所攜帶的信息量和對函數的貢獻不同[18]，逐步判別分析過程忽略了某些因素的影響，導致產生一定的誤差；二是用于建立判別函數的原始觀測數據的離散程度也是產生一定誤差的一個原因，原始數據有規律性且代表性強，所建立的判別函數精度就高，誤差就小，若原始數據比較離亂，所建立的判別函數精度就差，誤差就會偏大。從所選的原始數據建立判別函數和實際應用對比看，達到了較高的識別精度，能較好地滿足實際需要。

3 結論

(1)采用了逐步判別分析方法識別水淹層，從相關測井指標中優選出與油層水淹相關的指標來建立逐步判別函數，能有效識別水淹層級別，經實際檢驗，達到了較好的識別精度，為新北油田開發后期調整井水淹層識別提出了新的思路和方法。

(2)逐步判別分析方法已被多個領域廣泛應用，對于建立的判別函數的精度和實用性，取決于所選建立函數樣本數據的數量和代表性，已知樣品數量越多代表性越強時，所得的判別函數就越可靠，所以優選原始數據很重要。

(3)用新北油田數據建立的判別函數最適用于新北地區的油層水淹識別，而且效果非常好，但不一定適合其他地區的水淹層識別，針對不同地質特征油田用自己油田的數據建立不同的判別函數，才能有更好的識別效果。