新課標邏輯推理核心素養(yǎng)的解讀及培養(yǎng)策略

湖北

筆者有幸作為主要成員參加了宜昌市教科院主持的人民教育出版社課程教材研究所“十三五”課題《高中數(shù)學(xué)核心素養(yǎng)教學(xué)評價及其應(yīng)用研究》，在第二階段核心素養(yǎng)形成的基本過程中，通過研究《普通高中數(shù)學(xué)課程標準》(2017年)版發(fā)現(xiàn)，邏輯推理放在選修課程C類(人文類)課程部分，定位為為學(xué)生發(fā)展方向提供引導(dǎo)，為學(xué)生展示數(shù)學(xué)才能提供平臺，為學(xué)生發(fā)展數(shù)學(xué)興趣提供選擇，為大學(xué)自主招生提供參考，即數(shù)學(xué)學(xué)業(yè)質(zhì)量水平三要求的內(nèi)容，而在數(shù)學(xué)學(xué)業(yè)質(zhì)量水平一、二都提出了很高的要求，即對高中畢業(yè)及高考都有很高要求.在這種新形式下，對邏輯推理核心素養(yǎng)的水平要求及培養(yǎng)，成了一線教師必須認真研究的任務(wù).筆者談?wù)劀\顯看法以求拋磚引玉.

一、邏輯推理核心素養(yǎng)的學(xué)業(yè)質(zhì)量水平解讀

學(xué)生畢業(yè)水平要求能夠在熟悉的情境中，用歸納或類比的方法，發(fā)現(xiàn)數(shù)量或圖形的性質(zhì)、數(shù)量關(guān)系或圖形關(guān)系，能夠在熟悉的數(shù)學(xué)內(nèi)容中，識別歸納推理、類比推理和演繹推理，能夠了解通過歸納推理和類比推理得到的結(jié)論是或然成立的，通過演繹推理得到的結(jié)論是必然成立的.能夠通過熟悉的例子理解歸納推理、類比推理和演繹推理的基本形式.能夠了解熟悉的數(shù)學(xué)命題的條件與結(jié)論之間的邏輯推理關(guān)系，能夠掌握一些基本命題與定理的證明，并有條理地表述論證過程，能夠了解熟悉的概念、定理之間的邏輯關(guān)系,能夠在交流過程中，明確所討論問題的內(nèi)涵，有條理地表達觀點.

學(xué)生高考水平要求能夠在關(guān)聯(lián)的情境中，發(fā)現(xiàn)并提出數(shù)學(xué)問題，用數(shù)學(xué)語言予以表達；能夠理解歸納、類比是發(fā)現(xiàn)和提出數(shù)學(xué)命題的重要途徑.能夠?qū)εc學(xué)過的知識有關(guān)聯(lián)的數(shù)學(xué)命題，通過對條件與結(jié)論的分析，探索論證的思路，選擇合適的論證方法予以證明，并能用準確的數(shù)學(xué)語言表述論證過程，能夠通過舉反例說明某些結(jié)論不成立.能夠理解相關(guān)概念、命題和定理之間的邏輯關(guān)系，初步建立網(wǎng)狀知識結(jié)構(gòu)，能夠在交流的過程中，始終圍繞主題，觀點明確，論述有理有據(jù).

學(xué)生自主招生水平要求能夠在綜合的情境中，用數(shù)學(xué)的眼光找到合適的研究對象，提出有意義的數(shù)學(xué)問題.能夠掌握常用邏輯推理方法的規(guī)則，理解其蘊含的思想.對于新的數(shù)學(xué)問題，能夠提出不同的假設(shè)或前提，推斷結(jié)論，形成新的數(shù)學(xué)命題.對于較復(fù)雜的數(shù)學(xué)問題，能夠通過構(gòu)建過渡性命題，探索論證的途徑，解決問題，并會用嚴謹?shù)臄?shù)學(xué)語言表達論證過程.能夠理解建構(gòu)數(shù)學(xué)體系的公理化思想.能夠合理地運用數(shù)學(xué)語言和思維進行跨學(xué)科的表達與交流.

通過以上解讀發(fā)現(xiàn)，盡管邏輯推理內(nèi)容放在選修部分，但我們的日常教學(xué)要講述相關(guān)內(nèi)容，讓學(xué)生能夠掌握邏輯推理的基本形式，學(xué)會有邏輯地思考問題，能夠在比較復(fù)雜的情境中把握事物之間的關(guān)聯(lián)，把握事物發(fā)展的脈絡(luò)，形成重論據(jù)、有條理、合乎邏輯的思維品質(zhì)和理性精神，增強交流能力.

二、邏輯推理核心素養(yǎng)的表征

邏輯推理核心素養(yǎng)體現(xiàn)在以下四個方面：情境與問題、知識與技能、思維與表達和交流與反思.情境與問題：情境主要是指現(xiàn)實情境、數(shù)學(xué)情境和科學(xué)情境，問題是指在情境中提出的數(shù)學(xué)問題；知識與技能，主要是指能夠幫助學(xué)生形成邏輯推理核心素養(yǎng)的知識與技能；思維與表達，主要是指在數(shù)學(xué)活動中反映出的重論據(jù)、有條理、合乎邏輯的思維品質(zhì)和理性精神，以及表述的嚴謹性和準確性；交流與反思，主要是指能夠用數(shù)學(xué)語言解釋和交流數(shù)學(xué)概念、結(jié)論、應(yīng)用和思想方法內(nèi)部及之間的邏輯關(guān)系，并能進行評價、總結(jié)與拓展.

三、邏輯推理核心素養(yǎng)的培養(yǎng)策略

由于邏輯推理放在選修部分，知識的講授只能通過日常教學(xué)滲透.其他五大核心素養(yǎng)的培養(yǎng)離不開邏輯推理核心素養(yǎng)，毫不夸張地說，離開邏輯推理核心素養(yǎng)，數(shù)學(xué)活動將無法開展，數(shù)學(xué)教學(xué)無時無刻不在培養(yǎng)著邏輯推理核心素養(yǎng)，教師只要做一個有心人即可.

1.概念教學(xué)的合情推理和大膽猜想是培養(yǎng)邏輯推理核心素養(yǎng)的重要抓手

從培養(yǎng)邏輯推理核心素養(yǎng)角度出發(fā)，概念教學(xué)的流程可歸納為：情境引入→觀察、分析、比較、聯(lián)想→歸納、類比→大膽猜想→準確描述概念→交流、反思、拓展，其中第二、三步是核心.

案例1(人教A版必修1)：函數(shù)的概念

情境1(1)一枚炮彈發(fā)射后，經(jīng)過26 s落到地面擊中目標.炮彈的射高為845 m，且炮彈距地面的高度h(單位：m)隨時間t(單位：s)變化的規(guī)律是

h=130t-5t2. (﹡)

(2)近幾十年來，大氣層中的臭氧迅速減少，因而出現(xiàn)了臭氧層空洞問題.下圖中的曲線顯示了南極上空臭氧層空洞的面積從1979～2001年的變化情況.

(3)國際上常用恩格爾系數(shù)反映一個國家或地區(qū)人民生活質(zhì)量的高低，恩格爾系數(shù)越低，生活質(zhì)量越高.下表中恩格爾系數(shù)隨時間(年)變化的情況表明，“八五”計劃以來，我國城鎮(zhèn)居民的生活質(zhì)量發(fā)生了顯著變化.

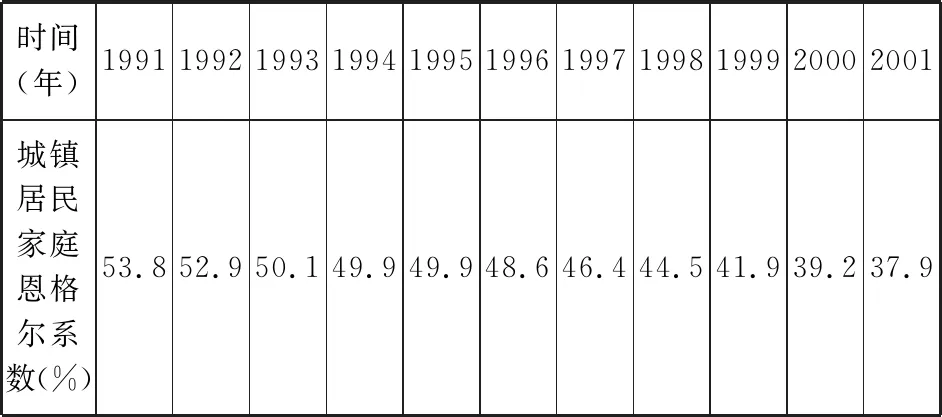
“八五”計劃以來我國城鎮(zhèn)居民恩格爾系數(shù)變化情況

(1)中，炮彈飛行時間t的變化范圍是數(shù)集A={t|0≤t≤26}，炮彈距地面的高度h的變化范圍是數(shù)集B={h|0≤h≤845}.由問題的實際意義可知，對于數(shù)集A中的任意一個時間t，按照對應(yīng)關(guān)系(﹡)，在數(shù)集B中都有唯一確定的高度h和它對應(yīng).

請你仿照(1)描述(2)中臭氧層空洞面積和時間(年)的關(guān)系及(3)中恩格爾系數(shù)和時間(年)的關(guān)系.

生1：(2)中，時間t的變化范圍是數(shù)集A={t|1 979≤t≤2 001}，臭氧層空洞面積S的變化范圍是數(shù)集B={S|0≤S≤26}.根據(jù)圖中的曲線可知，對于數(shù)集A中的任意一個時間t，在數(shù)集B中都有唯一確定的臭氧層空洞面積S和它對應(yīng).

生2：(3)中，時間t的變化范圍是數(shù)集A={t|1 991≤t≤2 001}，恩格爾系數(shù)s的變化范圍是數(shù)集B={s|37.9≤s≤53.8}.根據(jù)表中的數(shù)據(jù)可知，對于數(shù)集A中的任意一個時間t，在數(shù)集B中都有唯一確定的恩格爾系數(shù)s和它對應(yīng).

設(shè)計意圖：(1)(2)屬于現(xiàn)實情境，(3)屬于科學(xué)情境，告訴學(xué)生數(shù)學(xué)知識來源于生活及其他學(xué)科，數(shù)學(xué)是一門工具學(xué)科，要善于從現(xiàn)實生活情境及科學(xué)情境中發(fā)現(xiàn)我們要研究的問題.仿照(1)描述(2)中臭氧層空洞面積和時間(年)的關(guān)系及(3)中恩格爾系數(shù)和時間(年)的關(guān)系，讓學(xué)生從模仿開始培養(yǎng)交流能力，提升交流的條理性和嚴謹性.

情境2歸納實例(1)(2)(3)，用準確的語言描述三個實例中變量之間的關(guān)系(共性).

生3：對于數(shù)集A中的每一個數(shù)，在數(shù)集B中都有唯一確定的數(shù)和它對應(yīng).

師：分組討論，完善生3的發(fā)言.

生4:(1)中由問題的實際意義可知，(2)中根據(jù)圖中的曲線可知，(3)中根據(jù)表中的數(shù)據(jù)可知，不知怎么描述共性.

師：可按照某種對應(yīng)關(guān)系描述，對應(yīng)關(guān)系可以是解析式、圖象或表格.這種由某類事物的部分對象具有某些特征，推出該類事物的全部對象都具有這些特征的推理，或者由個別事實概括出一般結(jié)論的推理，統(tǒng)稱為歸納推理(簡稱歸納).簡言之，歸納推理是由部分到整體、由個別到一般的推理.應(yīng)用歸納推理可以發(fā)現(xiàn)新事實，獲得新結(jié)論.

設(shè)計意圖：教給學(xué)生歸納推理知識，培養(yǎng)歸納能力，養(yǎng)成用歸納發(fā)現(xiàn)新事實，獲得新結(jié)論的意識.

情境3(教師用PPT投影)歸納以上三個實例，三個實例中變量之間的關(guān)系都可以描述為：對于數(shù)集A中的每一個數(shù)x，按照某種對應(yīng)關(guān)系f描述，在數(shù)集B中都有唯一確定的數(shù)y和它對應(yīng)，記作f:A→B.

定義：設(shè)A，B是非空的數(shù)集，按照某種確定的對應(yīng)關(guān)系f，使對于數(shù)集A中的任意一個數(shù)x，在集合B中都有唯一確定的數(shù)f(x)和它對應(yīng)，那么就稱f:A→B為從集合A到集合B的一個函數(shù)，記作y=f(x)，x∈A.

其中，x叫做自變量，x的取值范圍A叫做函數(shù)的定義域；與x的值相對應(yīng)的y值叫做函數(shù)值，函數(shù)值的集合{f(x)|x∈A}叫做函數(shù)的值域.

設(shè)計意圖：投影標準描述，訓(xùn)練學(xué)生板書規(guī)范性，反思自己不足，接著給出函數(shù)定義，告訴學(xué)生知識來源于生活與其他學(xué)科情境以及產(chǎn)生方法.

情境4探究以下問題：

(1)為什么要求集合A，B是非空數(shù)集？

(2)在A中任取一元素，在B中有幾個元素與之對應(yīng)？在B中任取一個元素在A中有幾個元素與之對應(yīng)？值域與集合B是什么關(guān)系？

(3)“函”是什么意思？為什么稱f:A→B為從集合A到集合B的一個函數(shù)？再用“函”解讀(2).

設(shè)計意圖：以問題鏈的方式，讓學(xué)生對定義進行探究，反思、總結(jié)定義的內(nèi)涵及外延.(3)的目的是讓學(xué)生知道定義可通過內(nèi)涵加以命名，反之從命名可探究概念內(nèi)涵，加深對概念的理解并拓展.

2.命題證明的演繹推理和小心求證是培養(yǎng)邏輯推理核心素養(yǎng)的關(guān)鍵陣地

從邏輯推理核心素養(yǎng)培養(yǎng)角度出發(fā)，命題證明的流程可歸納如下：分析命題條件或結(jié)論探究證明所用理論(已知的一般原理：大前提)→分析理論條件及結(jié)論(改造成p→q形式)→分析題目條件(小前提)→結(jié)論(根據(jù)一般原理做出判斷)，具體操作可由因索果(綜合法)：P?Q1→Q1?Q2→Q2?Q3→……→Qn?Q，其中P表示條件、已有的定義、定理或公理等，Q表示所要證明的結(jié)論；也可由果索因(分析法)：Q?p1→p1?p2→p2?p3→……→得到一個明顯成立的條件，其中Q表示要證明的結(jié)論.

案例2(人教A版必修1P29)：

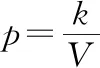
師：請將該問題轉(zhuǎn)化為數(shù)學(xué)問題，并解答.

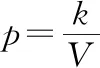
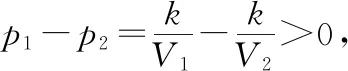
師：從一般性的原理出發(fā)，推出某個特殊情況下的結(jié)論，這種推理稱為演繹推理，一般模式為三段論，包括:

(1)大前提——已知的一般原理；

(2)小前提——所研究的特殊情況；

(3)結(jié)論——根據(jù)一般原理，對特殊情況做出判斷.

用符號語言可表述如下：

大前提：M?P；

小前提：S?M；

結(jié)論：S?P.

請分析此題的大前提，即所用知識點.

生2：大前提即理論依據(jù)，是減函數(shù)定義，若對于定義域I內(nèi)某個區(qū)間D上的任意兩個自變量的值x1，x2，當x1f(x2).

師：小前提生1板書是否正確？對應(yīng)大前提逐字逐句檢查.

生3：第一句缺少任意兩個實數(shù)V1,V2∈(0,+∞).

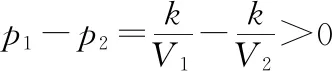
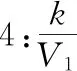
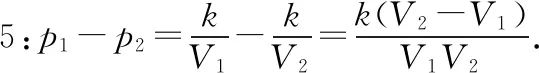
因為V1,V2∈(0,+∞)，所以V1V2>0.因為V10，所以p1-p2>0.

師：歸納用單調(diào)性定義證明單調(diào)性的步驟.

生6：取值→作差→變形→定號(每個部分的正負)→結(jié)論.

設(shè)計意圖：傳授演繹推理知識，訓(xùn)練三段論技能，形成重論據(jù)、有條理、合乎邏輯的思維品質(zhì)和理性精神，增強交流能力.

3.習(xí)題解答的探路搭橋是培養(yǎng)邏輯推理核心素養(yǎng)的核心陣地

一般來說，數(shù)學(xué)題海無涯，數(shù)學(xué)問題不勝枚舉，解法也千差萬別，十八般武藝統(tǒng)統(tǒng)用上.但是，我們解決問題的過程是類似的，可以用如下流程圖表示：

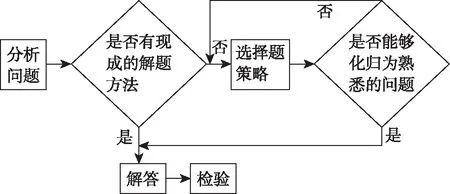
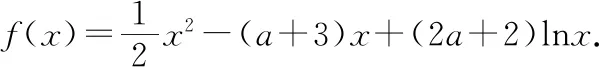
(1)函數(shù)f(x)在點(1,f(1))處的切線與2x-y+1=0平行，求a的值；

(2)討論函數(shù)f(x)的單調(diào)性；

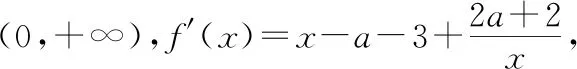
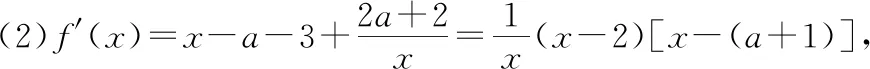
當a+1>2即a>1時,在[0,2]上,f′(x)≥0,f(x)單調(diào)遞增；在[2,a+1]上，f′(x)≤0，f(x)單調(diào)遞減；在[a+1,+∞)上，f′(x)≥0,f(x)單調(diào)遞增.

當a=1時，在(0，+∞)上，f′(x)≥0，f(x)單調(diào)遞增.

當-1

當a≤-1時,在[0,2]上，f′(x)≤0,f(x)單調(diào)遞減；在[2,+∞)上,f′(x)≥0,f(x)單調(diào)遞增.