對一道高考圓錐曲線試題的研究和拓展

陜西

隨著課改的進一步實施，高考的考查更具針對性和靈活性.考能力、考方法、考學生分析、解決問題的能力,為進一步提升學生的應對能力和適應能力，2018年高考落幕后，全國各地試卷中出現諸多具有研究價值和值得借鑒的好試題.

一、試題呈現

(2018·北京卷理·19)已知拋物線C：y2=2px經過點P(1，2).過點Q(0，1)的直線l與拋物線C有兩個不同的交點A，B，且直線PA交y軸于M，直線PB交y軸于N.

(Ⅰ)求直線l的斜率的取值范圍；

解：(Ⅰ)因為拋物線y2=2px經過點P(1，2)，所以4=2p，即p=2，故拋物線的方程為y2=4x.由題意知，直線l的斜率存在且不為0.

設直線l的方程為y=kx+1(k≠0).

又PA，PB與y軸相交，故直線l不過點(1，-2).從而k≠-3.

所以直線l斜率的取值范圍是(-∞，-3)∪(-3，0)∪(0，1).

做完這道題筆者做了一個大膽的猜想：第二問的結論能否對一般情況也成立呢？答案是肯定的，具體來看.

=2.

此結論對于拋物線是成立的，那么對于橢圓和雙曲線成立嗎？請和筆者一起來研究.

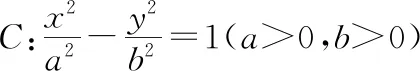
二、試題拓展及探源

此定理證明可仿照前面結論，由于篇幅有限，在此不再贅述.

只要思考，就有收獲.只有對問題做了深入的思考，才能體會到數學的奧妙及神奇，要多思考，正如此高考題一樣，首先要弄清此題的背景，這樣才有提高.在平時教學中要多思、多想，這樣數學會因思考而更加精彩，一個好的數學試題，除了問題本身精彩外，還應該具有推廣的潛力，是許多相關知識的交匯點.此題就具有這樣的推廣潛力.