基于密度峰值與密度聚類的集成算法

王治和 黃夢瑩 杜輝 秦紅武

摘 要：針對快速搜索和發(fā)現(xiàn)密度峰值聚類（CFSFDP）算法需人工在決策圖上選擇聚類中心的問題，提出一種基于密度峰值和密度聚類的集成算法。首先，借鑒CFSFDP思想，將局部密度最大的數(shù)據(jù)作為第一個中心;接著，從該中心點出發(fā)采用一種利用Warshall算法求解密度相連改進的基于密度的噪聲應用空間聚類（DBSCAN）算法進行聚類，得到第一個簇;最后，在尚未被劃分的數(shù)據(jù)中找出最大局部密度的數(shù)據(jù)，將它作為下一個簇的中心后再次采用上述算法進行聚類，直到所有數(shù)據(jù)被聚類或有部分數(shù)據(jù)被視為噪聲。所提算法既解決了CFSFDP選擇中心需人工干預的問題，又優(yōu)化了DBSCAN算法，即每次迭代都是從當前最好的點（局部密度最大的點）出發(fā)尋找簇。通過可視化數(shù)據(jù)集和非可視化數(shù)據(jù)集與經(jīng)典算法（CFSFDP、DBSCAN、模糊C均值（FCM）算法和K均值（K-means）算法）的對比實驗結(jié)果表明，所提算法聚類效果更好，準確率更高，優(yōu)于對比算法。

關(guān)鍵詞：密度峰值;密度聚類;Warshall算法;決策圖;聚類中心

中圖分類號： TP301.6

文獻標志碼：A

Abstract： In order to solve the problem that Clustering by Fast Search and Find of Density Peaks （CFSFDP） needs to manually select the center on the decision graph， an Integrated Algorithm Based on Density Peaks and Density-based Clustering （IABDPDC） was proposed. Firstly， learning from the principle of CFSFDP， the data with the largest local density was selected as the first center. Then， from the first center， Density-Based Spatial Clustering of Applications with Noise （DBSCAN） algorithm improved by Warshall algorithm was used to cluster to obtain the first category. Finally， from the data that has not been clustered， the maximum local density data was found out as the center of the next category and was clustered again by the above algorithm， until all the data was clustered or some data was considered as noise. The proposed algorithm not only solves the problem of manual center selection in CFSFDP， but also optimizes the DBSCAN algorithm， in which， every iteration starts from the current best point （the point with the largest local density）. By comparing with the classical algorithms （such as CFSFDP， DBSCAN， fuzzy C-means （FCM） and K-means） on visual datasets and non-visualized datasets， the experimental results show that the proposed algorithm has better clustering effect with higher accuracy.

Key words： density peak; density-based clustering; Warshall algorithm; decision graph; cluster center

0 引言

聚類分析試圖將相似的元素劃分為一類、不相似的元素劃分在不同類，廣泛應用于天文學、生物信息學、文獻計量學和模式識別[1-4]等領(lǐng)域。聚類分析是數(shù)據(jù)挖掘的重要模塊之一，其算法主要有基于劃分的算法、基于圖論的算法、基于密度的算法等。在基于劃分的算法中，最具代表性的是K-means[5]和K-medoids[6]，所劃分的類是數(shù)據(jù)到中心距離更小的那些數(shù)據(jù)的集合。這類算法都是先設(shè)定中心，然后通過計算目標函數(shù)和數(shù)據(jù)間距離以及不斷優(yōu)化中心，直到最適合的中心被找到[7];但是，這種聚類算法只是把數(shù)據(jù)分配給距離它更近的中心，只適應于凸數(shù)據(jù)。謝娟英等[8]提出了一種基于密度峰值初始化中心的K-medoids算法，能自動確定類的個數(shù)。在基于圖論的算法中，多路譜聚類算法[9]要求對數(shù)據(jù)建立相似度矩陣和拉普拉斯矩陣，計算特征值和特征向量，然后利用K-means算法進行聚類;但是該算法的時間復雜度和空間復雜度都比較高，還需要進一步的改進。周林等[10]利用采樣算法降低了譜聚類算法的計算復雜度，利用Nystrm采樣算法只計算隨機采樣數(shù)據(jù)點之間以及隨機采樣數(shù)據(jù)點與剩余數(shù)據(jù)點之間的相似度矩陣。在基于密度的聚類算法中，基于密度的噪聲應用空間聚類（Density-Based Spatial Clustering of Applications with Noise， DBSCAN）算法[11]通過建立數(shù)據(jù)的密度相連實現(xiàn)聚類，這種方法能發(fā)現(xiàn)任意形狀的簇，但是對閾值Eps（掃描半徑）和MinPts（最小包含點數(shù)）的依賴較大。Chen等[12]針對聚類中心測量困難和參數(shù)依賴性大的問題提出了一種新的聚類中心快速確定的聚類算法。戴陽陽等[13]提出了初始點優(yōu)化與參數(shù)自適應的DBSCAN算法，解決了閾值對密度不均勻數(shù)據(jù)聚類影響的問題。快速搜索和發(fā)現(xiàn)密度峰值聚類（Clustering by Fast Search and Find of Density Peaks， CFSFDP）算法[14]是基于局部密度和相對距離的算法，利用決策圖人工識別中心進行聚類，運算效率高，但并不是所有的數(shù)據(jù)集都能通過決策圖準確地找到中心并進行聚類。因此，利用CFSFDP算法尋找中心的方法不斷地被學者們研究，提出了各種各樣的方法。比如，文獻[15]提出了一種自動確定中心的CFSFDP算法，是基于基尼指數(shù)的自適應截斷距離和自動獲取聚類中心的方法，避免了決策圖人工選擇中心帶來的誤差。馬春來等[16]提出了一種自動選擇中心的密度峰值算法，根據(jù)中心權(quán)值的變化趨勢選擇“拐點”，以“拐點”之前的一組數(shù)據(jù)作為中心，避免了決策圖人工找中心的誤差。周世波等[17]提出了一種基于決策圖和相對密度的聚類算法，實現(xiàn)了快速尋找聚類中心并確定有效的類數(shù)。謝國偉等[18]提出了一種非參數(shù)核估計的CFSFDP算法，用非參數(shù)核估計的方法計算數(shù)據(jù)的局部密度并選擇潛在中心進行歸類，最后對相鄰類合并得到聚類結(jié)果。

通過上述研究，本文針對CFSFDP需要人工從決策圖上選擇中心的問題，提出了一種基于CFSFDP和DBSCAN的集成算法（Integrated Algorithm Based on Density Peaks and Density-based Clustering， IABDPDC）。在找到中心之后，對數(shù)據(jù)集的聚類設(shè)計了一種利用傳遞閉包的Warshall算法[19]求解密度相連的密度聚類，以便每次聚類都是從最優(yōu)點出發(fā)，而不是從傳統(tǒng)密度聚類的核心點出發(fā)。IABDPDC既解決了CFSFDP在確定中心時需人工在決策圖上選擇的問題，又優(yōu)化了DBSCAN算法。

1 相關(guān)工作

CFSFDP算法和DBSCAN算法都需要計算數(shù)據(jù)的局部密度，其中：CFSFDP算法是一種快速、高效的聚類算法，但決策圖需人工選擇中心;DBSCAN算法相比K-means算法，能對非凸數(shù)據(jù)聚類，但算法效率不高。Warshall算法則是一種計算相似關(guān)系的算法，本文擬利用Warshall算法實現(xiàn)DBSCAN算法的密度相連，以優(yōu)化DBSCAN算法。

1.1 CFSFDP算法

1.2 DBSCAN算法

DBSCAN算法是一種基于密度聚類的典型算法，可以實現(xiàn)對任意數(shù)據(jù)的聚類并識別噪聲，在Eps鄰域、核心點、直接密度可達、密度可達的基礎(chǔ)上，建立密度相連[20]，通過實現(xiàn)最大密度相連的集合對數(shù)據(jù)集進行聚類。DBSCAN算法需要識別數(shù)據(jù)集的噪聲點、邊界點和核心點，然后進行聚類。識別噪聲點之后，將所有在核心點Eps鄰域內(nèi)的數(shù)據(jù)與該核心點劃分為一簇，并對簇中未建立Eps鄰域的核心點建立Eps鄰域，建立最大密度相連集合，實現(xiàn)對簇的劃分。

DBSCAN算法中的密度相連也是一種數(shù)據(jù)間的傳遞關(guān)系，為使其密度相連過程更加簡單，設(shè)計一種改進的DBSCAN算法，即用Warshall算法求解傳遞閉包的過程代替DBSCAN算法的求解最大密度相連的過程。基于Warshall的DBSCAN算法在利用局部密度最大的數(shù)據(jù)是中心的想法找到中心后，再從中心點出發(fā)查找所有和中心點同一類的數(shù)據(jù)進行聚類，不需要識別數(shù)據(jù)集的噪聲點、邊界點和核心點，降低了程序的復雜性。

1.3 Warshall算法

Warshall[19]于1962年提出了求關(guān)系傳遞閉包的算法，并將它命名為Warshall算法，因其使復雜的二元關(guān)系的傳遞變得簡單化而被人廣泛學習和應用。該算法通過分析數(shù)據(jù)間的相似關(guān)系，求出相似關(guān)系的傳遞閉包。Warshall算法如下：

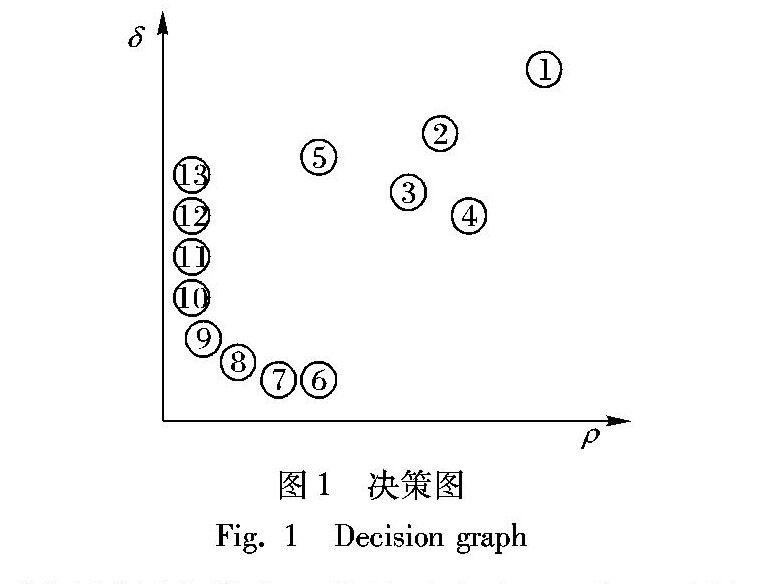
CFSFDP算法確定δi和ρi值都較大的數(shù)據(jù)i需要人工在決策圖（如圖1）上選擇，第一個中心就是最大局部密度的數(shù)據(jù)，它在決策圖的最右上方，第二或其他的中心為決策圖中δi和ρi值相對都較大的數(shù)據(jù)，也分布在決策圖的右上方，但應該選擇右上方的哪些數(shù)據(jù)作為中心是不好解決的問題。例如圖1，最右上方的數(shù)據(jù)1的局部密度是最大的，將它作為第一個中心，數(shù)據(jù)2、3、4的δi和ρi值相差不大，選擇哪個數(shù)據(jù)作為下一個中心是很難抉擇的問題。盡管有時通過計算γi=δiρi選擇γi值較大的數(shù)據(jù)作為中心，但選取多少個γi較大的數(shù)據(jù)點作為中心是不容易確定的。基于CFSFDP與DBSCAN的集成算法，可以準確地找出類簇的中心，避免了中心選擇不當造成的聚類錯誤。

從上述尋找到的中心（最好的點）出發(fā)利用密度聚類算法進行聚類，然而，傳統(tǒng)的密度聚類無法從最好的點出發(fā)聚類，而是需要找數(shù)據(jù)的核心點、直接密度可達點、密度可達點，進而找出數(shù)據(jù)的最大密度相連對數(shù)據(jù)進行聚類，聚類過程比較復雜，給程序造成了負擔。利用Warshall算法求解DBSCAN算法的最大密度相連，從聚類中心出發(fā)利用Warshall算法找出所有和該點相連的數(shù)據(jù)并將它們劃分為同一類降低了算法的復雜性。

3 實驗結(jié)果與分析

IABDPDC通過C語言編寫，用Matlab工具顯示實驗結(jié)果。通過對可視化數(shù)據(jù)集和非可視化數(shù)據(jù)集進行實驗，從而評估和分析所提算法，對比算法包括： CFSFDP、DBSCAN、FCM和K-means算法。其中：CFSFDP算法是一種快速搜索查詢的利用決策圖確定中心的算法;DBSCAN算法是基于密度的典型聚類算法;FCM算法[21]是一種基于拉普拉斯矩陣的聚類算法;K-means是一種只適應于凸數(shù)據(jù)的聚類算法;IABDPDC則是一種基于密度分析的聚類算法，不僅可以自動確定中心，且利用Warshall算法建立矩陣實現(xiàn)了對任意形狀數(shù)據(jù)的聚類。

4 結(jié)語

針對CFSFDP算法確定中心需要人工在決策圖上選擇的問題，提出了一種集成算法，將CFSFDP的思想（局部密度最大的數(shù)據(jù)是中心）和DBSCAN算法結(jié)合為一種新的算法IABDPDC。為降低算法的復雜性，還將DBSCAN算法求密度相連的過程設(shè)計為利用二元關(guān)系傳遞閉包的Warshall算法來求解。IABDPDC每次從未被聚類的數(shù)據(jù)出發(fā)將局部密度最大的數(shù)據(jù)作為中心，利用改進的DBSCAN算法從最優(yōu)點出發(fā)進行聚類，既解決了CFSFDP算法選擇中心需人工干預的問題，又優(yōu)化了DBSCAN算法。實驗對比與分析表明，IABDPDC能得到較好的聚類結(jié)果，但部分聚類結(jié)果仍受到閾值的影響，下一步將研究自適應的聚類算法，減少閾值對聚類結(jié)果的影響，使算法的聚類結(jié)果達到最優(yōu)。

參考文獻：

[1] HE H， TAN Y. Automatic pattern recognition of ECG signals using entropy-based adaptive dimensionality reduction and clustering [J]. Applied Soft Computing，2017， 55： 238-252

[2] PENG C， KANG Z， XU F， et al. Image projection ridge regression for subspace clustering [J]. IEEE Signal Processing Letters， 2017， 24（7）： 991-995.

[3] R？THLISBERGER V， ZISCHG A P， KEILER M. Identifying spatial cluster of flood exposure to support decision making in risk management [J]. Science of the Total Environment， 2017， 598： 593-603.

[4] SUZUKI S， KAKUTA M， ISHIDA T， et al. Faster sequence homology searches by clustering subsequences [J].Bioinformatics， 2015， 31（8）： 1183-1190.

[5] MACQUEEN J B. Some methods for classification and analysis of multivariate observations [C]// Proceedings of the 1967 5th Berkeley Symposium on Mathematical Statistics and Probability. Berlin： Springer， 1967： 281-297.

[6] KAUFMAN L. ROUSSEEUW P J. Finding groups in data： an introduction to cluster analysis [M]. New York： John Wiley & Sons， 1990： 74.

[7] HOPPNER F， KLAWONN F， KRUSE R， et al. Fuzzy cluster analysis-methods for classification [J]. Journal of the Operational Research Society， 1998， 51（6）：769-770.

[8] 謝娟英，屈亞楠.密度峰值優(yōu)化初始中心的K-medoids聚類算法[J].計算機科學與探索，2016，10（2）：230-247.（XIE J Y， QU Y N. K-medoids clustering algorithms with optimized initial seeds by density peaks [J]. Journal of Frontiers of Computer Science and Technology， 2016， 10（2）：230-247.）

[9] NG A Y， JORDAN M I， WEISS Y. On spectral clustering： analysis and an algorithm [C]// NIPS01Proceedings of the 2001 International Conference on Neural Information Processing Systems： Natural and Synthetic. Cambridge， MA： MIT Press， 2001：849-856.

[10] 周林，平西建，徐森，等.基于譜聚類的聚類集成算法[J].自動化學報，2012，38（8）：1335-1342. （ZHOU L， PING X J， XU S， et al. Cluster ensemble based on spectral clustering[J]. Acta Automatica Sinica， 2012， 38（8）：1335-1342.）

[11] ESTER M， KRIEGEL H-P， SANDER J， et al. A density-based algorithm for discovering clusters in large spatial databases with noise [C]// KDD96： Proceedings of the Second International Conference on Knowledge Discovery and Data Mining. Menlo Park， CA： AAAI Press， 1996：226-231.

[12] CHEN J， LIN X， ZHENG H， et al. A novel cluster center fast determination clustering algorithm [J]. Applied Soft Computing， 2017， 57： 539-555.

[13] 戴陽陽，李朝鋒，徐華，等.初始點優(yōu)化與參數(shù)自適應的密度聚類算法[J].計算機工程，2016，42（1）：203-209. （DAI Y Y， LI C F， XU H， et al. Density spatial clustering algorithm with initial point optimization and parameter self-adaption [J]. Computer Engineering， 2016， 42（1）： 203-209.）

[14] RODRIGUEZ A， LAIO A. Clustering by fast search and find of density peaks [J]. Science， 2014， 344（6191）：1492.

[15] 王洋，張桂珠.自動確定聚類中心的密度峰值算法[J].計算機工程與應用，2017，2018， 54（8）：137-141. （WANG Y， ZHANG G Z. Automatically determine density of cluster center of peak algorithm [J]. Computer Engineering and Applications， 2017， 2018， 54（8）： 137-141.）

[16] 馬春來，單洪，馬濤.一種基于簇中心點自動選擇策略的密度峰值聚類算法[J].計算機科學，2016，43（7）：255-258. （MA C L， SHAN H， MA T. Improved density peaks based clustering algorithm with strategy choosing cluster center automatically [J]. Computer Science， 2016， 43（7）： 255-258.）

[17] 周世波，徐維祥.一種基于相對密度和決策圖的聚類算法[J].控制與決策，2018，33（11）：1921-1930. （ZHOU S B， XU W X. A novel clustering algorithm based on relative density and decision graph [J]. Control and Decision， 2018， 33（11）： 1921-1930.）

[18] 謝國偉，錢雪忠，周世兵.基于非參數(shù)核密度估計的密度峰值聚類算法[J/OL].計算機應用研究，2018 [2018-04-06]. http：//www.arocmag.com/article/02-2018-10-018.html. （XIE G W， QIAN X Z， ZHOU S B. Density peak clustering algorithm based on non-parametric kernel density estimation [J]. Application Research of Computers， 2018 [2018-04-06]. http：//www.arocmag.com/article/02-2018-10-018.html.）

[19] WARSHALL S. A theorem on Boolean matrices [J]. Journal of the ACM， 1962， 9（1）：11-12.

[20] 劉淑芬，孟冬雪，王曉燕.基于網(wǎng)格單元的DBSCAN算法[J].吉林大學學報（工學版），2014，44（4）：1135-1139. （LIU S F， MENG D X， WANG X Y. DBSCAN algorithm based on grid cell[J]. Journal of Jilin University （Engineering and Technology Edition）， 2014， 44（4）：1135-1139.）

[21] PAL N R， BEZDEK J C. On cluster validity for the fuzzy c-means model [J]. IEEE Transactions on Fuzzy Systems， 1995， 3（3）： 370-379.

[22] PAPADIMITRIOU C H， STEIGLITZ K. Combinatorial optimization： algorithms and complexity [M]. Upper Saddle River， NJ： Prentice-Hall， 1982.https：//dl.acm.org/citation.cfm？id=31027與原稿完全不同IEEE Transactions on Acoustics Speech & Signal Processing， 1982， 32（6）：1258-1259.