基于融合權重的云模型在西昌某地區(qū)地下水水質評價中的應用

康小兵，李 科，朱志強，劉慶賀，劉 希

(成都理工大學 地質災害防治與地質環(huán)境保護國家重點實驗室，成都 610059)

0 引 言

隨著國家居民需求和基礎建設需水量的增加，我國在很多城市均采用地下水源作為居民日常生活飲用水源和工農業(yè)用水水源。因此，如何通過正確有效的模型對地區(qū)地下水水質進行評價，以定量的形式了解地區(qū)水質變化情況和地下水水體的污染程度尤為重要，以此才能為該地區(qū)水資源的科學利用提供必要的理論依據(jù)。截至目前國內學者在地下水水質評價領域進行了深入研究，總結出適用于不同環(huán)境條件下的水質評價模型。目前主流使用的有內梅羅指數(shù)法[1]、主成分分析法[2]、模糊數(shù)學綜合評價[3]、層次分析法、BP神經(jīng)網(wǎng)絡算法[4]及投影尋蹤算法模型[5]等。上述模型各有其適用局限性，如內梅羅指數(shù)法存在在評價指標過多時，評分階段極易受到污染因子最大值的影響，同時在分級標準評價時數(shù)值不連續(xù)，影響最終評價結果；主成分分析法使得函數(shù)意義出現(xiàn)極大模糊性，對客觀評價結果準確性造成缺失；模糊數(shù)學容易突顯極值作用從而導致評價結果失真；單一層次分析法在確定權重因素時易受到主觀因素影響，不利于評價結果的準確性，神經(jīng)網(wǎng)絡算法過程過于復雜，計算過程容易出錯，不利于一線人員的掌握。

隨著李德毅院士在1995年提出云模型概念，針對自然界物質的模糊性和隨機性，提出隸屬正向云發(fā)生器可表現(xiàn)自然界中由定性到定量之間的轉換[6]，同時于2004年證明了云模型的普適性[7]，在這十余年間也得到了各行業(yè)的廣泛應用[8-10]。因水質綜合評價中指標和分級標準具有一定的模糊性和隨機性特點，造成部分方法難以準確的判斷和掌握水質情況的現(xiàn)狀，近幾年引進正態(tài)云模型應用于地下水水質評價當中，并進行了與實際結果的比較，大部分監(jiān)測點評價結果較為不錯，部分有差異性存在[11-13]。

本文根據(jù)監(jiān)測點實測數(shù)據(jù)值基于正態(tài)云模型建立評價體系，為減小權重值所帶來的誤差影響，采取主觀層次分析法(AHP)和客觀GRITIC賦權法相結合，進行綜合賦權，使得評價結果更為準確，再將評價結果與模糊數(shù)學綜合評價法和實際結果進行雙重比較，驗證評價體系的合理性，同時對正態(tài)云模型評價過程中所存在差異性的問題提出見解。云模型評價流程如圖1所示。

圖1 評價流程示意圖Fig.1 Schematic diagram of the evaluation process

1 基于組合賦權的權重確定

1.1 AHP主觀賦權法

層次分析法[13]指代將決策按照不同層次，將復雜問題逐層簡化為單層問題，單層次指標的重要性順序由專家咨詢小組進行兩兩對比，構建出單層次判斷矩陣A，通過計算定量化描述后檢驗矩陣A的一致性，CR<0.1則判定通過，反之則對矩陣進行調整直至通過檢驗。

1.1.1 構建判斷矩陣

設該層次共有n個指標(表1)，對其進行ni(i=1,2,…,n)和nj(j=1,2,…,n)，由此構成含有aij的n階矩陣A：

(1)

1.1.2 權重向量

構建判斷矩陣后，需計算求得矩陣最大特征值和特征向量，本文采取方根法計算，繼而得到特征向量的分量W，即為權重值：

計算矩陣A每一行的乘積得到Ai：

(2)

對Ai的值開n次方：

(3)

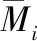
(4)

根據(jù)W和A計算出最大特征值λmax：

(5)

1.1.3 一致性檢驗

引入平均隨機一致性指標RI(表2)，計算所得驗證系數(shù)CR。檢驗公式如下：

(6)

式中：n為單層次參與評價指標數(shù)。

表2 平均隨機一致性指標RITab.2 Average random consistency index RI

通過一致性檢驗后即單層次權重值確定，如若最高層下只有一層，該層排序即為層次總排序。該方法不足在于主觀性較強，可能出現(xiàn)結果與實際的偏離誤差。

1.2 CRITIC客觀賦權法

CRITIC賦權法是由Diakoulaki1995年提出的客觀賦權法[14]，賦權基礎決定于兩個方面，其一是同一指標在不同方案中取值差距的大小，用標準差予以量化比較；其二是賦權過程中不同指標之間的沖突性大小，以相關性為比較標準，相關性越大則沖突性較小，反之亦然。最后得出不同指標的信息量大小，即為其權重值大小。主要步驟如下。

(1)確定不同指標的標準差σ：

(7)

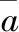
(2)確定指標a和b之間的沖突性量化值：

(8)

ηab=1-ρab

(9)

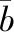
(3)信息量的計算：

(10)

式中：ρij為第i個指標和第j個指標的相關系數(shù)值。

(4)第i個指標的客觀權重值：

(11)

GRITIC優(yōu)勢在于不受主觀因素的影響，遵照實測數(shù)據(jù)賦予指標不同權重，缺點在于容易受到實測誤差的影響，以及實測過程中某種特殊原因產(chǎn)生指標極大值導致賦權結果失真。

1.3 組合賦權

因單一賦權法存在的局限性，本文在博弈論的基礎上采取組合賦權方式，融合主客觀的優(yōu)點，彌補不足之處，從而尋求最優(yōu)權重值。主要步驟如下[15]：

(1)求解最優(yōu)化線性組合系數(shù)(α1α2…αN)：

(12)

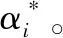
(2)進行最優(yōu)化權重矩陣(W)求解：

(13)

2 云模型的構建

2.1 正態(tài)云模型理論

關于云是如何定義的，隸屬度和隸屬云的介紹等，前人已經(jīng)進行了詳細闡述，不再贅述[6]。正態(tài)云模型是將人類對于自然界事物認識中的模糊性和隨機性結合在一起，實現(xiàn)定性概念到定量描述之間的互相轉換。其定性概念基于一組3個相互獨立的參數(shù)所表現(xiàn)出來，從而形成云滴，構建出云模型[7]：

期望Ex：云滴在論域空間的期望，表示概念在論域空間中的中心值，在水質評價中則為最典型樣本值。

熵En：在云模型中表示定性概念可度量的粒度，表示定性概念模糊程度的度量和在論域空間的離散程度，熵越大，概念也就越宏觀，離散程度也越大，形象的表達出水質評價等級之間的模糊性。

超熵He：指代熵的熵，表現(xiàn)的是熵的不確定性，由熵的模糊性和隨機性所決定，其大小在圖中最直接的反饋是所構建云層的厚度，即反映了云滴的凝聚程度，當He=0時，正態(tài)云即為正態(tài)曲線。

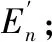
正向云發(fā)生器構建云模型目前多結合MATLAB進行算法演算，本文采用Python基于ATOM編輯器進行編程計算，相對于MATLAB優(yōu)點在于其完全開源，可清楚看到代碼運算過程并進行算法細節(jié)的添加、刪減。對于掌握清楚云發(fā)生器運算過程和對其進行二次開發(fā)應用的讀者使用較為方便。

2.2 云模型特征參數(shù)的確定

在進行上述評價之前，需根據(jù)水質評價對象和分級標準確定相對應的云特征參數(shù)(Ex、En、He)[16]：

Ex=(xij+xij)/2

(14)

式中：xij和xij分別為該指標雙邊約束中的分級上下限值，若是為單邊約束條件，可直接根據(jù)地區(qū)地下水超標污染物的值進行計算。

在進行水質評價過程中，因邊界值對于相鄰等級歸屬性的模糊性存在，其隸屬度相同，單邊約束條件下可直接根據(jù)超標污染物的值進行計算，式(16)為式(15)的簡化：

(15)

(16)

He表示熵的模糊性，通常取值為k，可根據(jù)云層厚度和離散程度進行調整取值范圍。

3 工程實例

3.1 工程概況與數(shù)據(jù)來源

評價區(qū)位于四川省西昌市城西約12 km的安寧河中游地帶，地勢北高南低，評價面積約16 km2。評價區(qū)內水系屬金沙江主干支流雅礱江水系，主要發(fā)育河流為安寧河，以及安寧河上各山間次級沖溝、溪流等。數(shù)據(jù)來源于評價區(qū)20個監(jiān)測點共20組樣品，實測樣品經(jīng)分析后發(fā)現(xiàn)存在部分點位指標超標，主要超標因子為三氮和硫元素，僅有一個點位發(fā)現(xiàn)錳超標，未發(fā)現(xiàn)鐵離子超標，少數(shù)點位水質等級達到Ⅳ，已對當?shù)鼐用耧嬎】敌纬赏{(見圖2)。

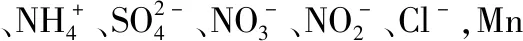
3.2 評價過程

3.2.1 權重計算

表3為本次結合調查報告和地下水指標對水質影響程度所構建的判斷矩陣A，進行一致性檢驗得出λmax=9.629 9，CR=0.053 9<0.1，判斷矩陣A通過檢驗，得出權重WAHP。將表3數(shù)據(jù)進行無量綱化處理，得出標準差和信息量值，從而計算出權重WCRITIC。通過博弈論組合權重確定方法，求解出最優(yōu)權重值W優(yōu)，3組權重矩陣如表4所示。

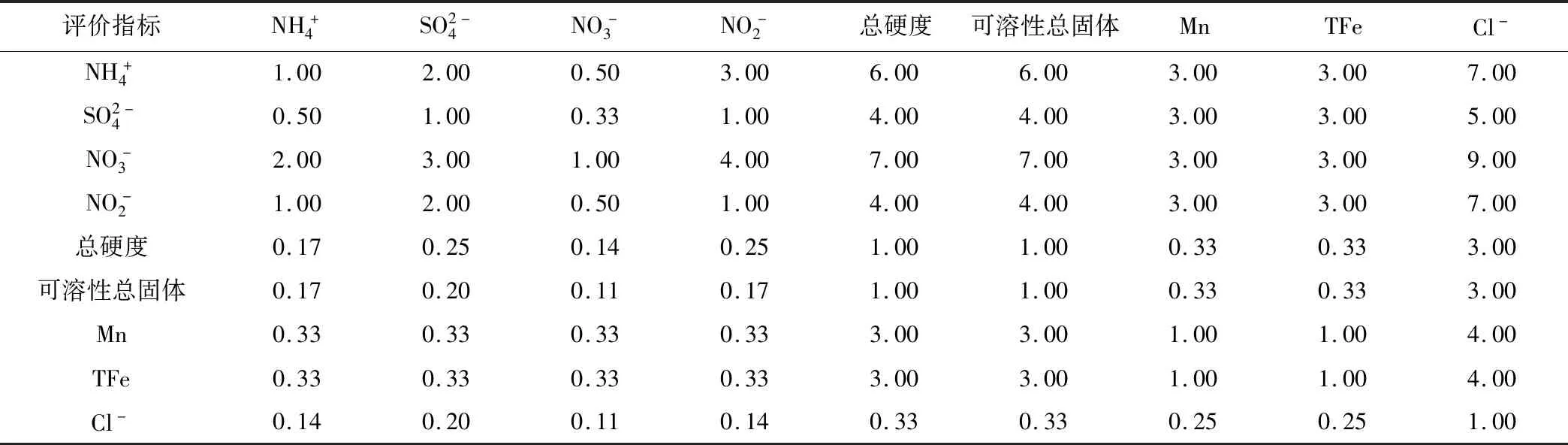
表3 判斷矩陣Tab.3 Judgment matrix

圖2 現(xiàn)場監(jiān)測點布置示意圖Fig.2 Schematic diagram of site monitoring point layout

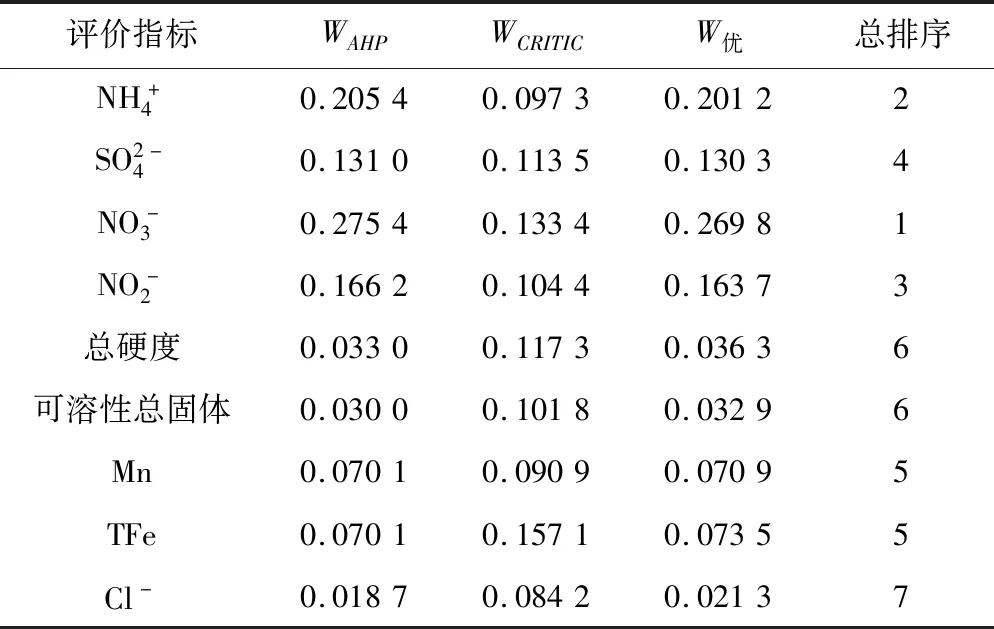
表4 不同方法的指標權重值Tab.4 Index weight value for different methods

3.2.2 計算確定度

(1)依據(jù)《中華人民共和國地下水質量標準》GB-T-14848-2017，構建云特征參數(shù)(Ex、En、He)，見表5。

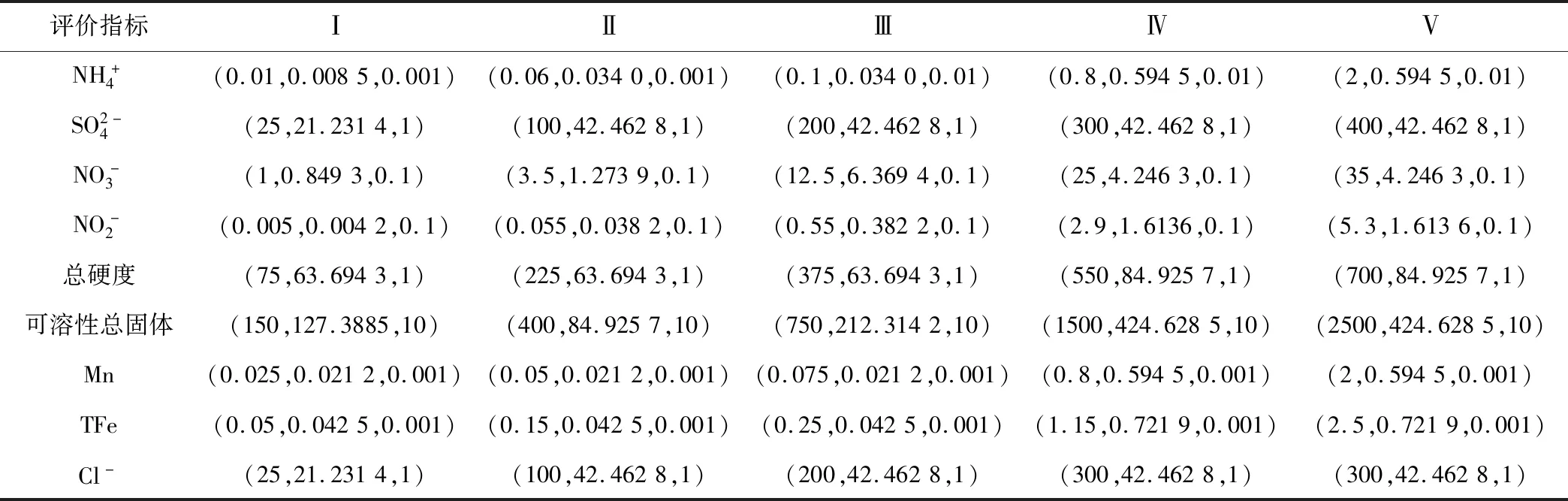
表5 不同指標的云特征參數(shù)Tab.5 Cloud characteristic parameters of different indicators

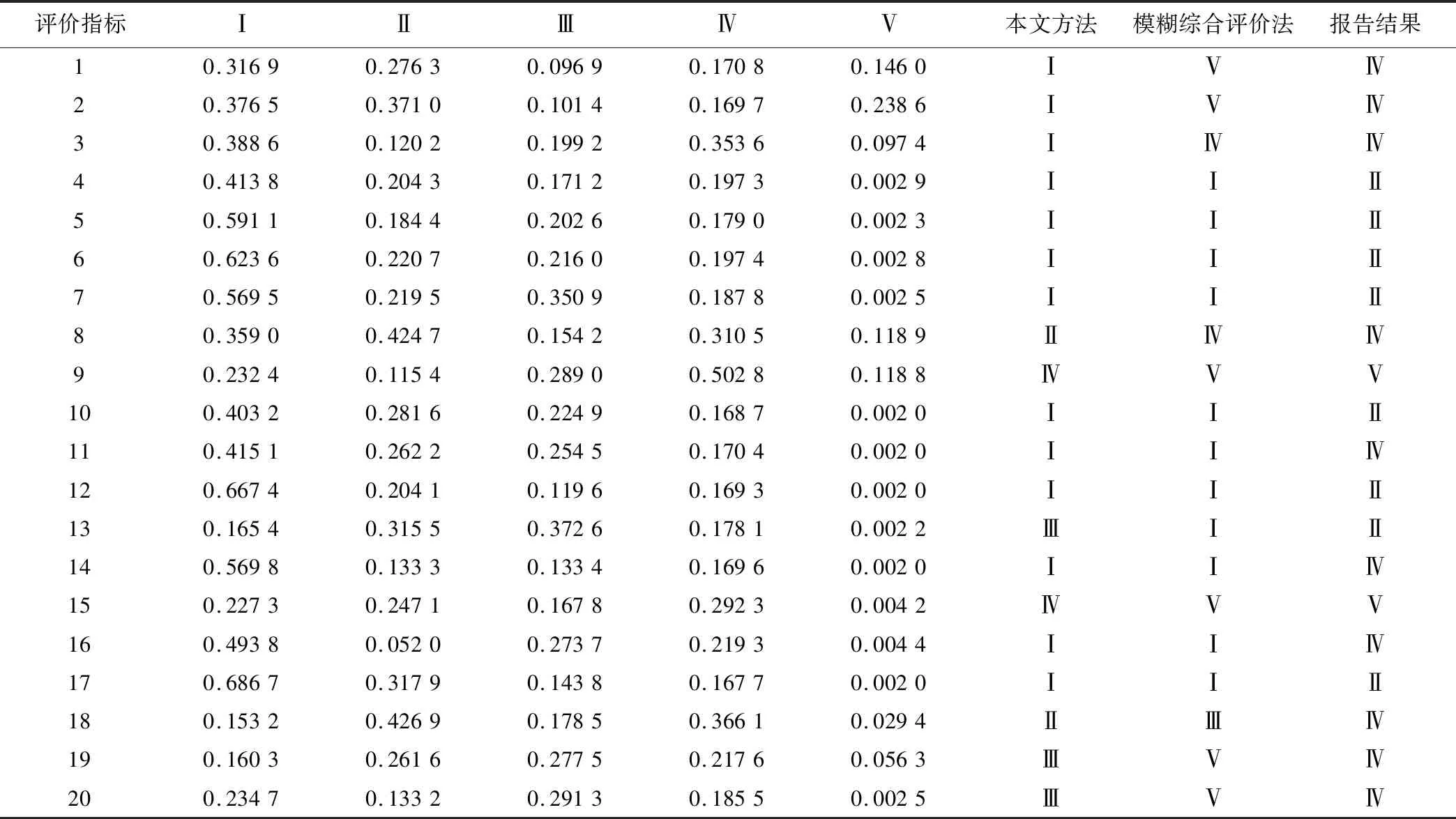
表6 水質評價結果Tab.6 Assessment results of groundwater quality

3.3 結果分析

(1)對比表6中3種方法的水質評價結果，除去前三組水質評價結果相差較大，其他結果均差別很小，其中云模型相較于模糊綜合評價法和內梅羅指數(shù)評價結果更為偏向好的一面，這是因為內梅羅指數(shù)是基于F值評分分級，計算值相對集中于極大值影響因素從而忽略了較好水質級別[1]。模糊綜合評價則在評價過程中，當指標集個數(shù)較多，在權重矢量和為1的條件約束下，相對隸屬度權系數(shù)偏小，造成權重矢量與隸屬度模糊矩陣的相乘加大誤差性，出現(xiàn)等級模糊現(xiàn)象，在文中評價過程中甚至出現(xiàn)過Ⅰ類水和Ⅳ類水確定度僅差0.02的現(xiàn)象。本文基于組合賦權的云模型更好的規(guī)避了以上的誤差，在主客觀雙重賦權下權重值顯得貼近實際地區(qū)地下水污染環(huán)境，隸屬度的計算單獨基于云特征參數(shù)和實測數(shù)據(jù)，單邊約束條件下的云特征參數(shù)直接取超標污染物的值進行計算，利用熵值和超熵減小了極大值的影響程度和評價過程中的模糊性，在重復計算下消除結果的誤差性，綜合使得正態(tài)云模型評價結果更為準確，也證明了本文方法的可行性。

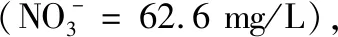
(3)在運用正態(tài)云模型對某地區(qū)進行水質評價過程中，針對單一指標超標情況可結合其余評價方法做出綜合評價。同時，在對云模型隸屬度計算公式研究中發(fā)現(xiàn)，目標指標的期望值與其隸屬度值存在反比關系。因此，在此提出一個構想(僅為正態(tài)云模型用于進行水質評價過程)，若僅存在單一超標污染物，其他指標實測數(shù)據(jù)遠小于Ⅰ、Ⅱ類水質標準限值，可試著更改近幾年以《地下水質量分級標準》選擇云特征參數(shù)的方式，根據(jù)污染物實測數(shù)據(jù)對云特征參數(shù)進行選擇，主觀降低期望值數(shù)據(jù)，從而消除單指標超標所帶來的誤差。

表7 不同指標在不同水質級別下的隸屬度(樣品1)Tab.7 Membership of different indicators at different groundwater quality levels (sample 1)

4 結 語

本文在基于AHP-CRITIC組合賦權的基礎上，運用正態(tài)云模型對西昌市某地區(qū)地下水水質進行綜合評價，得到結果與模糊綜合評價法和報告結果相似，評價結果準確可靠，具備一定的科學性和可行性。同時，在運用正態(tài)云模型評價過程中同樣發(fā)現(xiàn)了部分問題，在如何消除單一污染物指標超標而其他指標均處于較低值時對水質評價結果的影響方面，提出了兩個方向，其一是使用正態(tài)云模型進行水質評價時可結合其他評價方法進行綜合選擇；其二是對云特征參數(shù)的選擇根據(jù)實測值數(shù)據(jù)作出修改和調整，通過調整模型得到期望與指標實測值之間的反比系數(shù)，以主觀判斷的手段降低其他指標實測極小值所帶來的誤差性，具體做法留待后續(xù)研究討論。