基于優化模擬退火算法的航天薄壁結構件車間布局優化

彭劼揚，王家海，沈 斌

（1.同濟大學 機械學院，上海 201804；2.同濟大學 中德學院，上海 201804）

0 引言

航天產品加工過程復雜，大多數加工生產都是根據工藝人員的經驗進行設施規劃和加工，生產效率低下。在提高生產效率的方面，設施布置設計被視為提高車間生產力的關鍵[1]。研究表明，20%～50%的操作費用是用于原料運輸費用中。而工廠布局屬于NP問題，使用數值計算方法很難高效地解決，目前大都使用啟發式算法[2]或使用計算機軟件仿真進行求解。

對于布局問題，國外最早于1961年由Richard Muther研究出系統布置設計SLP方法，首次提出對于相互作用的生產單元之間的關系表示法，對后續相關研究打下堅實的基礎[3]。隨著科技的發展，SLP的缺點漸漸凸現出來，科研人員開始使用啟發式算法和SLP相結合的方式，衍生出改進法[4]。Ravi Kothari和Diptesh Ghosh[5]提出使用兩個禁忌算法對單行設施布局進行實現的策略，其中一個禁忌算法是窮舉搜索的2-opt鄰域，而另一個涉及插入鄰域的窮盡搜索，能夠加快兩個鄰域的搜索。齊繼陽和竺長安[6]使用改進型模擬退火算法，使用禁忌表的手段，增加了退火算法的記憶能力。龐峰[7]將改進SA算法應用到板式家具問題上，使材料利用率普遍高于95%。

基于以上研究，本文主要對對設備布局算法進行研究，提出了混合算法的一般設計原則。通過對比分析，發現將模擬退火思想應用到遺傳算法中能提升算法的收斂性，減少迭代次數。并在此基礎上，應用Plant Simulation仿真軟件對某航天大型零件車間布局進行仿真，驗證了混合算法的優越性。

1 數學模型

本文是對塊狀工位進行研究，對于塊狀的工位，需要考慮到一個設備所需的運維面積及該工位所需的工位面積。給定長×寬的時候，進行布局，則每一行的寬度由該行中最大寬度設備塊決定。布置過程如圖1所示，其中單行布置可以看成多行布置的特殊形式。

圖1 設備布局

而相應的數學模型可以表示如下：

其中：F是目標函數值；Cij為物料運輸費用；fij為物料運輸量；dij為兩個設備之間的距離；xixj為兩個設備之間x坐標值；yiyj為兩個設備之間y坐標值；lilj為設備i，j的長度；wiwj為設備i，j的寬度；L，H分別為車間的總長度和總寬度。

式(1)中，以物流量為優化目標，能夠很大程度上達到對車間的布局優化；式(2)中，dij作為兩個設備之間的距離，設備之間通常不能直接接觸的，距離的大小是通過兩個設備塊中心之間的直線距離進行衡量的；式(3)中主要是對同一行中兩臺設備在X軸方向進行限定，保證兩臺設備不交；式(4)中則是不同行相鄰設備之間在Y方向上不能交叉；式(5)是對車間長度方向的約束，不能超過車間規定的總長；式(6)是在車間寬度方向進行的限制，不能超差。基于以上公式的約束可以保證建模的合理性。

2 混合算法的設計

算法間存在多種結合方式，但是并不是所有的結合方式都能使新算法優于單個算法，因此對于兩個算法的結合應遵循以下原則進行：1）算法優缺點結合原則：相結合的兩個算法能夠優缺點互補，如此混合算法將優于獨立算法。或者盡量減少兩個算法缺點的相同部分，從而減小了對混合算法在該部分的進一步弱化；2）解形式一致原則：在算法結合過程中，注意解的聯系，兩個算法的結合部分注意解的形式的變換，如：遺傳算法中采用的是編碼的方式進行計算的，但是在粒子群算法中采用的是粒子的方式，在形式上有所區別。3）遵循適用原則：在處理具體問題的時候，有些算法不適合解決該問題的時候，就不能再使用該算法與其他算法進行結合來解決問題。

本文對于模擬退火遺傳算法進行的結合能夠同時滿足以上原則，能夠進行算法融合，混合算法流程如圖2所示。

圖2 混合算法流程

算法描述如下：

1）首先設置參數，種群數量，迭代次數，交叉率，變異率，初始溫度等；

2）采用退火原理對初代進行處理；

3）使用遺傳算法進行選擇、交叉、變異，方式如上文所述；

4）計算適應度值，進行比較，產生下一代種群；

5）產生子代后，若滿足收斂條件則輸出最優解，否則繼續進行迭代操作直到找出最優解。

3 混合算法的實例驗證

多行布局中在進行坐標求解時，按中心點的X坐標和Y坐標進行表示每個設備的位置。本算例采用文獻[8]中某機械加工企業，車間內設備的擺放方式是以機群為主。而且在其中生產的產品的質量較大，因此車間物流量相對較大。該車間是一個長為20m的正方形形狀車間，進行產品加工的設備有10臺，物流成本如下所示：

設備長度：{4.3，4.3，4.65，2，5，3.5，1.8，3.85，5，5}；

設備寬度：{5.6，3.7，7.75，4，4.2，5，2，4，4，4}。

單位成本矩陣如表1所示。

表1 費用矩陣

車間的初始布局為{1，2，3；4，5，6；7，8，9，10}，此時車間運輸成本為3748.8元。本文選取算法種群大小為10，子代數目為8的情況下，最大代數迭代到100，交叉率為0.8，變異率為0.2。

表為三種算法運行結果對比如表2所示。

表2 算法結果對比

多行布局平均值收斂曲線如圖3所示，其中橫坐標為迭代次數，縱坐標為物流運輸當量值，即是前文所述目標函數值。

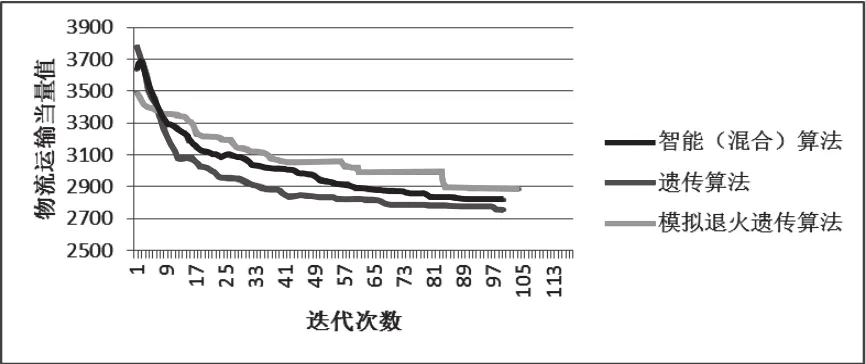
圖3 10次平均值迭代曲線

收斂曲線如圖4所示。

求解結果分析：

1）圖4中可知，10次混合算法平均解的收斂速度明顯高于遺傳算法和模擬退火算法。混合算法的10次解中只有第四次和第五次的解比遺傳算法稍差，其他的解均優于遺傳算法，而混合算法十次解中均優于模擬退火算法的解。

2）根據圖3中對比可以看出，混合算法的結果明顯優于其他另外兩種方式，混合算法在30代左右收斂到最好結果，而其他兩個算法在40代以后得到最終結果，且最優解相比混合算法較差，因此，混合算法的收斂特性和最優解均優于單獨算法。

圖4 最優解收斂曲線

4 基于Plant Simulation的布局算法仿真

航天薄壁結構件生產車間的情況較為復雜，涉及多品種小批量的混流生產，本文驗證的車間生產兩種型號的火箭儲箱，其中產品A是由6個筒段和2個箱底組成，而產品B是由6個筒段和2個箱底組成，年產量為12個貯箱。

使用Plantsimulation仿真軟件進行二維仿真，由混合算法得出的結果得出布局方案，如圖5所示，優化后的布局為（1，2，3；5，16，4，9，13，7，15，12；14，10，8，11，6），在Plant Simulation構建二維及三維仿真模型如圖5所示：

圖5 車間二維、三維布局圖

圖6 仿真運行結果

由仿真結果可知，生產相同產品的情況下，經過布局優化后的車間加工時間大大縮短，圖5所示經過改進后的仿真運行結果：

由圖6可知，在生產同樣零件個數的情況下，加工時間由365天縮短到204天左右，生產效率極大的提高了。

5 結束語

本文主要對現有航天產品車間進行改造，通過對布局算法的研究，分析遺傳算法和模擬退火算法從而設計出混合算法，并進行了算法驗證，得出了算法的有效性。通過混合算法對車間布局進行求解，獲得了車間布局優化方案。仿真結果表明：該混合算法具有很好的收斂特性，同時能夠得出較為理想的結果。