基于Elman網絡和實時遞歸學習的洪水預報研究

萬新宇，華麗娟，孫淼焱，鐘平安

(河海大學水文水資源學院，江蘇南京210098)

我國洪澇災害發生頻繁，經濟損失巨大[1]。準確預報洪水過程是減輕洪水災害的一項重要的非工程措施[2]。目前，洪水預報方法較多，大體可分為模型驅動與數據驅動兩類。模型驅動利用各類基于物理機制的水文模型進行洪水預報，如新安江模型[3]、TOPKAPI模型[4]和TOPMODEL[5]等。此類模型能詳細描述流域洪水形成過程，預報精度高，應用廣泛；但對資料要求高，除了基本的降雨徑流資料外，還需要流域蒸發、地形地貌和土地利用等資料的支撐[6]。當資料要求得不到滿足時，人們常常依據統計理論構建降雨徑流數據驅動模型，如ARMA[7]、NARX[8]和神經網絡模型[9]等。其中，以神經網絡模型應用最為流行。

神經網絡模型一般分為靜態網絡和動態網絡[10]。靜態網絡主要有反向傳播網絡[11]、徑向基網絡[12]和廣義回歸網絡[13]等。其中，以應用反向傳播網絡進行洪水預報最為普遍[14-15]。然而，流域洪水過程是一個復雜的非線性的動態過程，當前時刻洪水流量受到前期若干時段的降雨、徑流以及流域狀態的影響，靜態網絡一般難以反映這種動態特征[16]。相反，動態網絡因具有反饋連接和延遲結構而能夠反映系統的動態變化過程，如Elman網絡[17,18]和NARX網絡[19]。為此，本文以淮河流域響洪甸水庫為例，基于Elman網絡構建洪水預報模型，采用實時遞歸學習算法進行模型訓練，并對模型預測性能進行評價。

1 研究方法

1.1 Elman動態網絡

本研究基于三層感知機，構建動態神經網絡，其中包含1個輸入-輸出聯結層、1個隱含層和1個輸出層，具體結構如圖1所示。網絡有M個外部輸入和K個輸出。x(t)為網絡在t時刻的M×1維外部輸入向量，z(t+1)為網絡在t+1時刻的K×1維輸出向量，y(t+1)為網絡在t+1時刻隱含層的N×1維輸出向量。聯結外部輸入向量x(t)和隱含層延遲輸出向量y(t)，得(M+N)×1維向量u(t)，其中ui(t)代表其第i個元素，即

(1)

式中，A為外部輸入xi(t)的下標集；B為隱含層單元輸出yi(t)的下標集。

網絡的輸入-輸出聯結層與隱含層之間完全互連，其中有M×N個前向連接和N×N個反饋連接。W表示網絡的N×(M+N)維遞歸權重矩陣。為了使每個單元都有一個偏置值，本研究在M個輸入中總包含一個值為1的輸入。隱含層與輸出層也是完全互連，V表示K×N維權重矩陣。

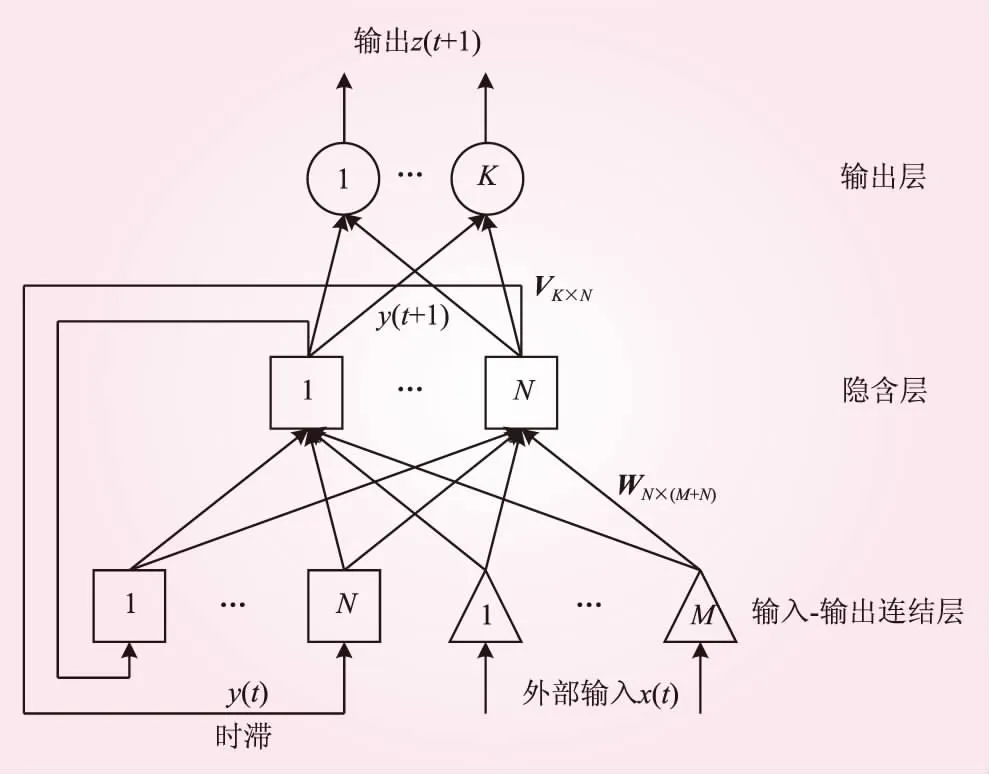
圖1 Elman動態網絡結構

計算t時刻網絡隱含層中神經元j的凈輸入，j∈B。即

(2)

再由傳輸函數f1(·)得到隱含層神經元j在t+1時刻的輸出，即

yj(t+1)=f1(netj(t))

(3)

計算網絡輸出層神經元k在t+1時刻的凈輸入netk(t+1)和輸出zk(t+1)。即

(4)

zk(t+1)=f2(netk(t+1))

(5)

式中，f2(·)為隱含層到輸出層的傳輸函數。值得注意的是，t時刻的外部輸入直到t+1時刻才會影響神經元的輸出。上述系統構成完整的動態網絡，本研究中傳輸函數f1(·)和f2(·)分別取tanh函數和線性函數。

1.2 性能函數

定義t時刻的網絡輸出K×1維時變誤差向量e(t)，其第k個元素為

ek(t)=dk(t)-zk(t)

(6)

式中，dk(t)為t時刻輸出層神經元k的目標值。定義網絡t時刻的瞬時誤差平方和為

(7)

則網絡所有時刻的總誤差為

(8)

1.3 實時遞歸學習算法

(9)

(10)

式中，η2為學習參數。又有

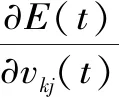
(11)

同理，可以求得各時刻權重wmn的變化

(12)

式中，η1是學習參數。

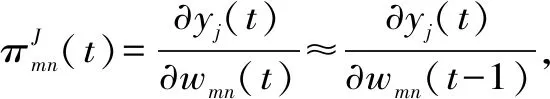
(13)

(14)

式中,j∈B,m∈B，n∈A∪B；δmj為克羅內克函數，當且僅當j=m時，δmj=1；否則，等于0。

假設時刻時t=0網絡的初始狀態與其權重無關，即

(15)

利用實時遞歸學習算法訓練如圖1所示Elman動態網絡，步驟如下：

(1)從開始，對每一時刻，用網絡的動態方程式(2)和(3)計算隱含層N個神經元的輸出，從而求出聯合輸入ui(t)(i∈A∪B)；再用動態方程式(4)和(5)計算輸出層K個神經元的輸出。對權重的初值可賦以均勻分布的隨機數。

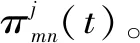
(16)

(4)按式(17)修正權重wmn和vkj

(17)

重復上述計算，直到誤差滿足一定的精度。

上述方法中，從初始時刻開始，每一時刻修正一次權重，使用的是瞬時誤差的梯度，與總誤差的梯度不同。當學習參數較小時，兩者效果差別不大[20]。

2 研究實例

2.1 流域與水庫概況

本研究以響洪甸水庫為例，進行入庫洪水預報研究。響洪甸水庫位于大別山區淮河流域淠河西源的安徽省金寨縣境內，流域面積1 431 km2。上游主要支流有燕子河、宋家河、姜家河，其中燕子河經張沖流入水庫，宋家河和姜家河在青山匯合后流入庫內。流域設有5座雨量站和2座水文站，具體分布如圖2所示。流域內地勢南高北低，均是山區坡地匯流，匯流時間短。地質構造簡單，以水成變質巖分布最廣，其次為火成變質巖和火山巖。流域內植被較好，多為野生灌木叢。地表面與巖面覆蓋層一般為0.5 m左右，滲透性較好。響洪甸水庫地處江淮之間，位置偏南，氣候接近長江流域。降雨主要受季風控制，多年平均降水量1 519.8 mm，7、8月降雨頻繁且雨量大，易造成洪水。

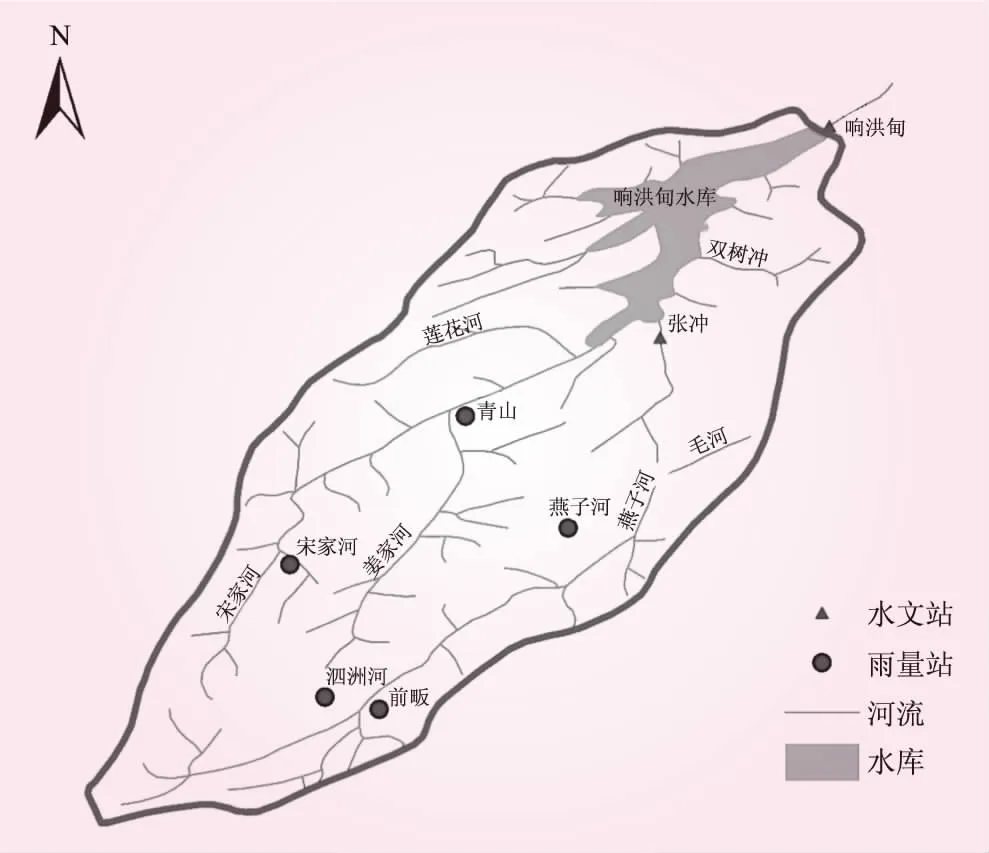
圖2 響洪甸水庫流域示意

本研究收集到響洪甸水庫流域1998年至2006年間31場洪水資料，主要包括宋家河和響洪甸兩站的雨量資料、響洪甸水庫水位、出庫流量以及水位庫容曲線等資料。根據水量平衡原理，反推響洪甸水庫入庫洪水過程?？紤]大中小不同量級的洪水過程，選擇其中16場洪水進行模型訓練，剩余15場洪水進行模型測試。計算時段長取1 h，以上時段雨量和入庫流量為模型輸入，預報下時段水庫入庫流量。模型結構為3個外部輸入單元，4個隱含層單元和1個輸出單元，隱含層向輸入層的反饋延遲1個時段。

2.2 結果與討論

利用訓練集中16場洪水，對上述模型進行訓練，模擬洪水過程。采用洪水總量誤差、洪峰流量誤差、峰現時刻差和確定性系數等指標評價各場洪水的模擬誤差，訓練結果見表1。

由表1可見，模型訓練后對各場洪水的模擬精度總體較高，洪水總量和洪峰流量的相對誤差絕對值平均為0.79%和4.17%，峰現時刻差平均為1.06小時，確定性系數平均值達到0.979。但各評價指標離散程度有所差別，洪峰流量相對誤差離散程度要大于洪水總量相對誤差離散程度，其變化范圍為[-1.13%，10.6%]，而洪水總量相對誤差變化范圍為[-0.38%，2.75%]。峰現時刻差變化范圍為[-8，1]，確定性系數的變化范圍為[0.868，0.999]。

通過訓練，確定了模型參數W和V，并利用該模型對預測集中15場洪水進行預測，預測結果見表2。

圖4為部分洪水的預測過程。由圖表可見，模型對預測集中15場洪水的預測精度也較高，洪水總量和洪峰流量的相對誤差絕對值平均為1.22%和4.24%，兩者均略高大于訓練誤差。但確定性系數平均值與模型訓練時相同，且峰現時刻差小于模型訓練時的峰現時刻差。相對于訓練結果，除峰現時刻差之外其他3個指標的離散程度均大于模型訓練時的離散程度。洪水總量相對誤差變化范圍為[-5.23%， 2.49%]，洪峰流量相對誤差變化范圍為[-5.02%， 12.6%]，確定性系數變化范圍為[0.857， 1.000]。

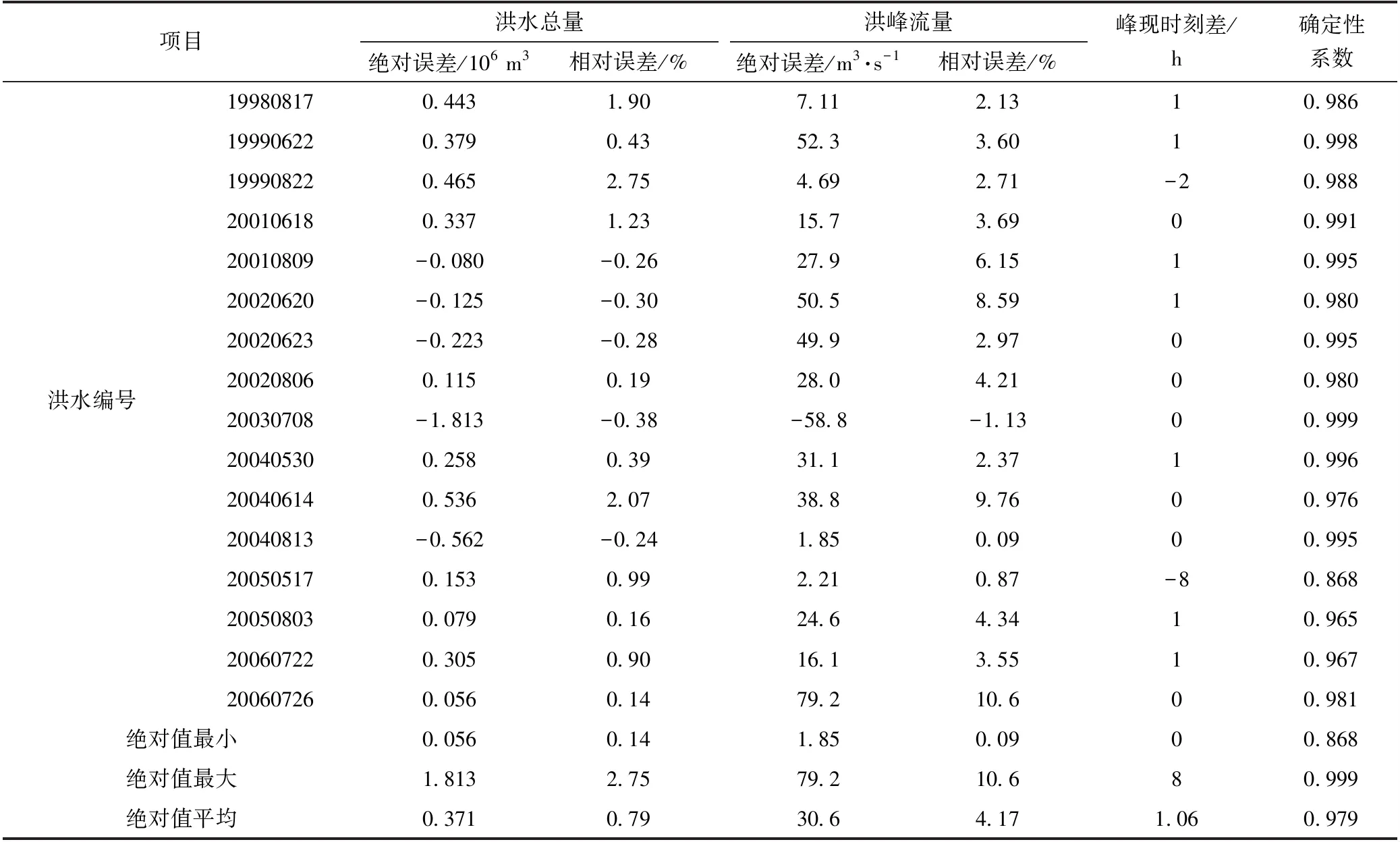
表1 訓練集中16場洪水的模擬結果

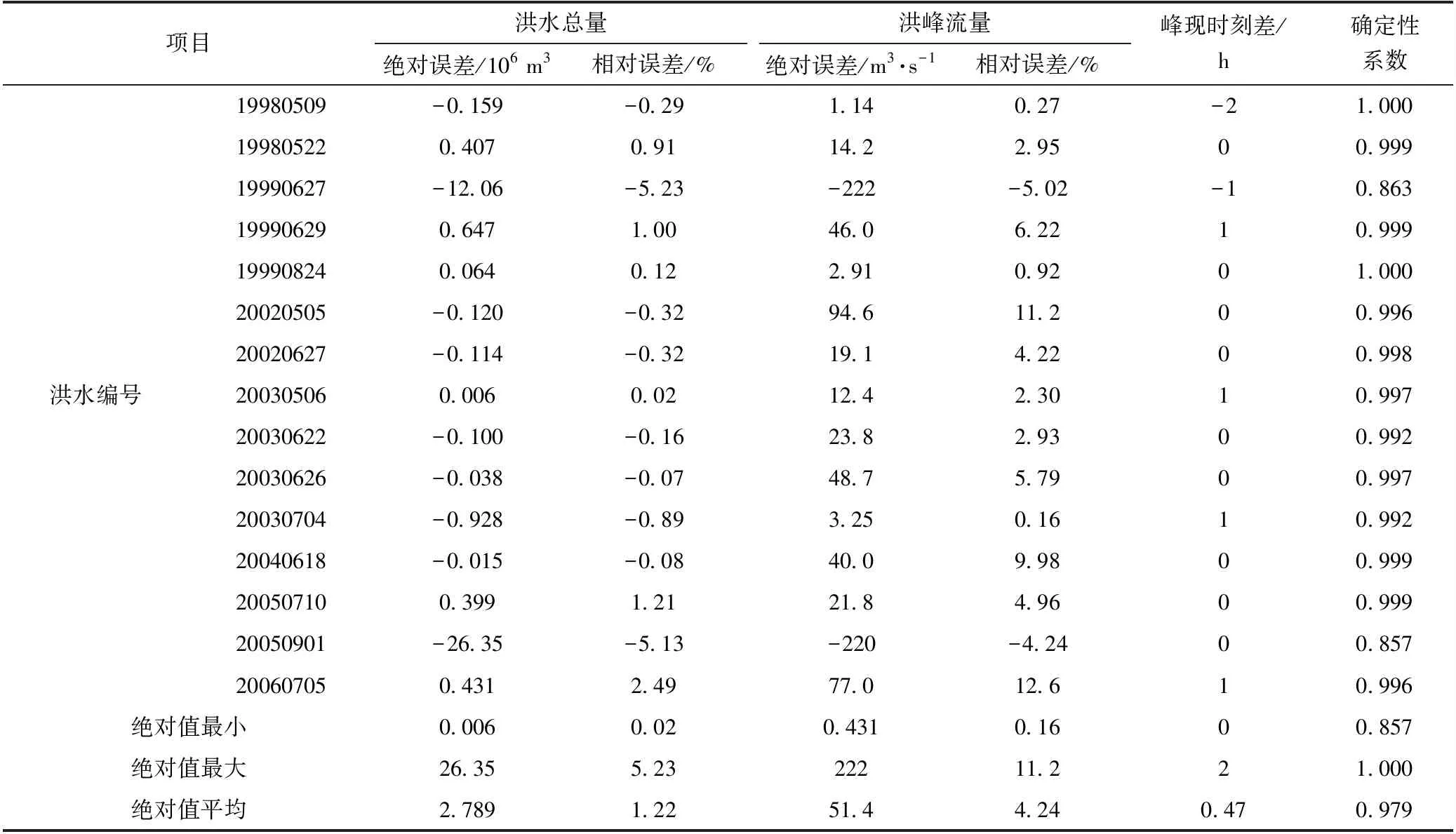
表2 測試集中15場洪水的預測結果

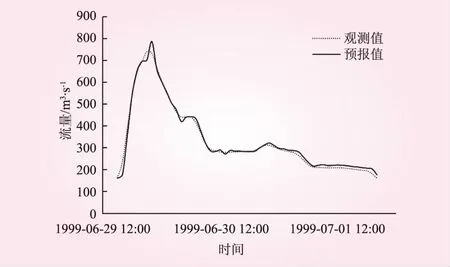
圖3 19990629號洪水預報過程

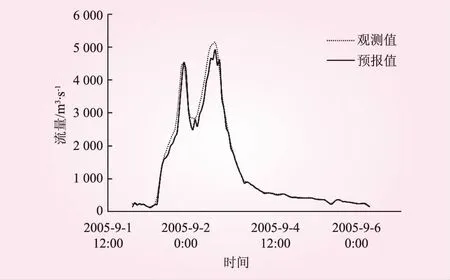
圖4 20050901號洪水預報過程

3 結 論

通過上述實例研究，得到以下結論：

(1)利用動態神經網絡構建洪水預報模型，模型輸出不僅依賴于當前模型當前輸入，而且還依賴于前期模型輸入和模型狀態，很好地反映了流域洪水動態變化特征。

(2)利用實時遞歸學習算法進行模型訓練，隨時間進程實時修正網絡權重，使得該算法和動態網絡模型能夠很好地適應實時洪水預報的要求。

(3)基于Elman網絡的響洪甸水庫洪水預報模型能夠得到較高的預報精度，洪水總量和洪峰流量的相對誤差絕對值平均為1.22%和4.24%，確定性系數平均達到0.979。

然而，本研究中采用的預見期較短，需要在后續研究中進一步研究較長預見期的動態網絡實時洪水預報模型，以更好地滿足防洪決策要求。