摩擦擺支座隔震連續梁橋抗震分析的簡化計算方法

李 健，邵長江

(1.中國鐵路總公司建設管理部，北京 100844；2 西南交通大學 土木工程學院，四川 成都 610031)

橋梁通過在橋墩上設置減隔震支座等，將地震輸入的動能轉化為支座摩擦耗能和動能，從而減小了傳遞給橋墩的地震力，同時結構基本周期的延長使其遠離了地震峰值加速度區段(從反應譜的角度看)，降低了結構的動力響應[1-3]。由于減隔震支座能夠顯著改善結構的抗震性能，被廣泛應用于強震區的橋梁工程中，是橋梁抗震設計中的重要減災措施和研究課題。摩擦擺隔震(Friction Pendulum System，FPS)支座是Zayas等[4]提出的一種有效的干摩擦滑移隔震體系，它通過摩擦滑移件在球形凹面上的滑動進行隔震。摩擦擺隔震支座具有對地震激勵頻率范圍低敏感性和抗震性能高穩定性的特點，特有的圓弧滑動面使其具有自復位功能，無需附設阻尼向心機構。與普通的摩擦滑移隔震支座相比，它很好地利用了擺的原理，通過上部結構的自重提供回復力，從而有效減小結構在震后的殘余位移[5-8]。采用減隔震措施后的橋梁比延性橋梁的抗震計算方法復雜。基于此，本文通過建立摩擦擺隔震梁橋的簡化模型，提出隔震連續梁橋的抗震簡化計算方法，并通過對比分析有限元結果和簡化計算結果來驗證模型和算法的合理性。

1 摩擦擺支座隔震梁橋的簡化算法

摩擦擺支座具有結構緊湊、物理模型簡單、抗震機理可靠的優點。采用摩擦擺支座(見圖1)的橋梁可以簡化為質量彈簧力學系統(見圖2)。

圖1 摩擦擺支座示意

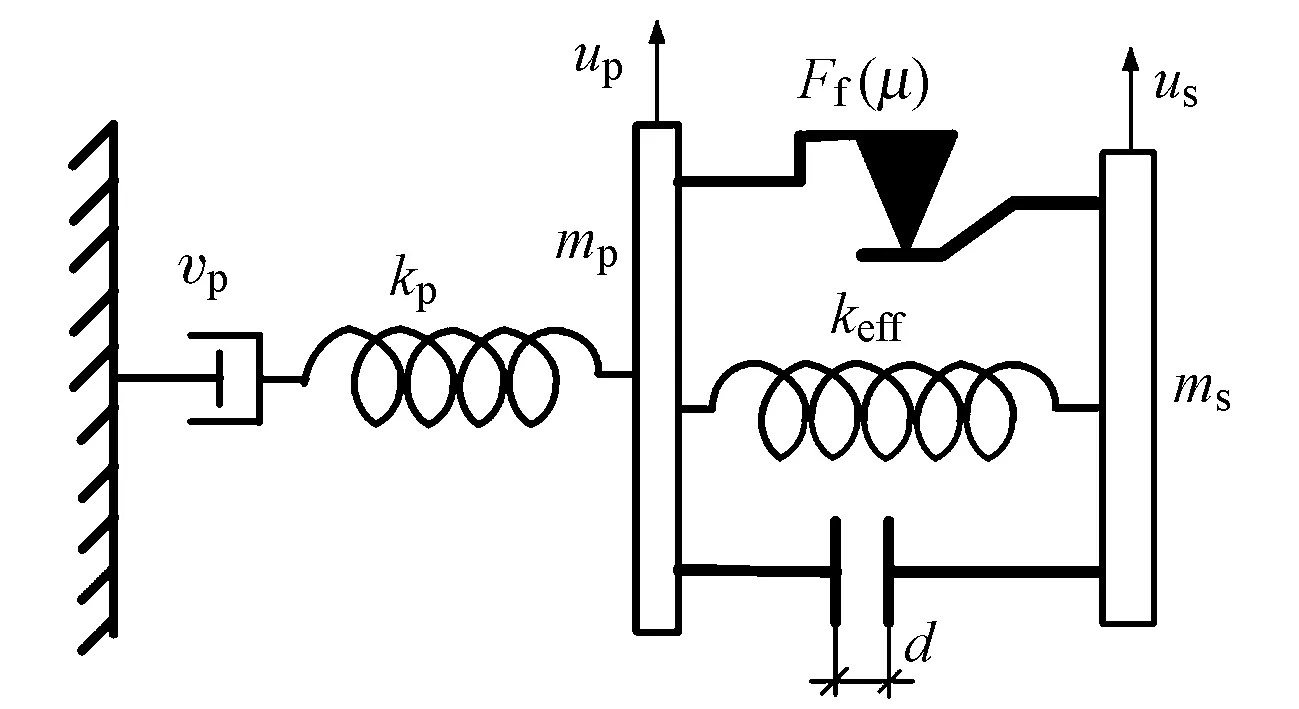
圖2 摩擦擺支座系統簡化模型

圖2中：keff為摩擦擺的等效剛度；Ff(μ)為摩擦擺支座的摩擦力；d為摩擦擺支座的設計位移；kp為橋墩剛度；vp為橋墩結構的阻尼；mp和ms分別為橋墩和上部結構的質量。

小振幅擺動時，摩擦擺支座的側向力F等于回復力Fe與摩擦力Ff之和[8]，即

(1)

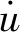
摩擦擺支座通過結構自重沿滑動曲面的切線方向的分力提供回復力，幫助上部結構回到原來的位置。如同普通鐘擺一樣，摩擦擺支座上部的結構也有一個振動周期，即

(2)

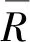
研究發現滑動面上的動摩擦因數與支座的運動形態相關，滑動摩擦因數的大小依賴于滑塊的運動速度和曲面上的壓力，表達式為

(3)

式中：μmax為滑動穩定時的最大摩擦因數，取0.06；μmin為速度極小時的摩擦因數，取0.02；a為速度相關系數，取20。

對結構進行反應譜或等效線性分析時，應將支座進行等效線性化處理，得到該支座的等效剛度和等效阻尼比[9]，分別為

(4)

(5)

只要合理選取地震下支座的設計位移d、半徑R和摩擦因數μ，就能滿足不同的減隔震設計要求。設梁橋的第i個橋墩剛度為kp,i，單個橋墩與其上隔震支座的串聯剛度為Keq，則縱橋向結構總體等效剛度為上述所有串聯剛度的總和，即

(6)

主橋一聯的換算質量Mt[9]為

Mt=Ms+ηpMp+ηbMb

(7)

式中：Ms，Mp，Mb分別為上部結構、橋墩和固定蓋梁的質量；ηp，ηb分別為橋墩和蓋梁的質量換算系數，計算時應考慮地基變形的影響。

由上述結構的等效剛度和換算質量可得結構的等效周期為

(8)

減隔震結構的等效阻尼比為

(9)

式中：di為第i個支座的設計位移；ξp,i為第i個橋墩的等效阻尼。

根據全橋結構有限元模型的動力特性計算結果，該結構基本周期為4.117 s，參照CJJ 166—2011《城市橋梁抗震設計規范》[9]，當結構基本周期大于5.0Tg=1.65 s(Tg為特征周期)時，反應譜曲線為

S=2.25[0.02γη1-η2(T-5Tg)]Amax

(10)

式中：γ為反應譜曲線下降段的衰減指數；η1為反應譜直線下降段下降斜率調整系數；η2為阻尼調整系數；Amax為地震動加速度峰值。

由反應譜曲線和結構的等效周期可得到簡化后的支座設計位移，即

(11)

隔震支座設計位移求解的迭代過程為：先設定摩擦擺的摩擦因數，根據式(2)得到支座的振動周期；由式(4) 和式(5)分別計算得到摩擦擺的等效剛度和等效阻尼比；根據式(6)和式(7)分別得到結構的等效剛度和等效質量；根據式(8)和式(9)分別得到結構的等效周期和等效阻尼比；根據式(10)得到等效結構的反應譜曲線。在此基礎上由式(11)可以得到隔震結構的最大位移。當設計位移和最大位移的相對誤差小于5%時，認為所得數值即為支座的設計位移。

2 工程概況及簡化模型

2.1 工程概況

一大橋主橋部分橋跨布置為(61+108+61)m三跨連續梁橋(如圖3所示)，主梁采用變截面預應力混凝土箱梁，輔助結構的拱肋為鋼箱截面，左右兩幅主梁在橋墩處通過橫梁連接。中支點處梁高6.5 m，跨中梁高2.5 m。主墩高9.0 m，過渡墩高15.0 m，主墩及過渡墩截面均為實心矩形雙柱式橋墩，兩墩柱通過系梁連接。基礎采用群樁基礎，中間墩樁長90.0 m，左邊過渡墩樁長83.0 m，右邊過渡墩樁長87.0 m。

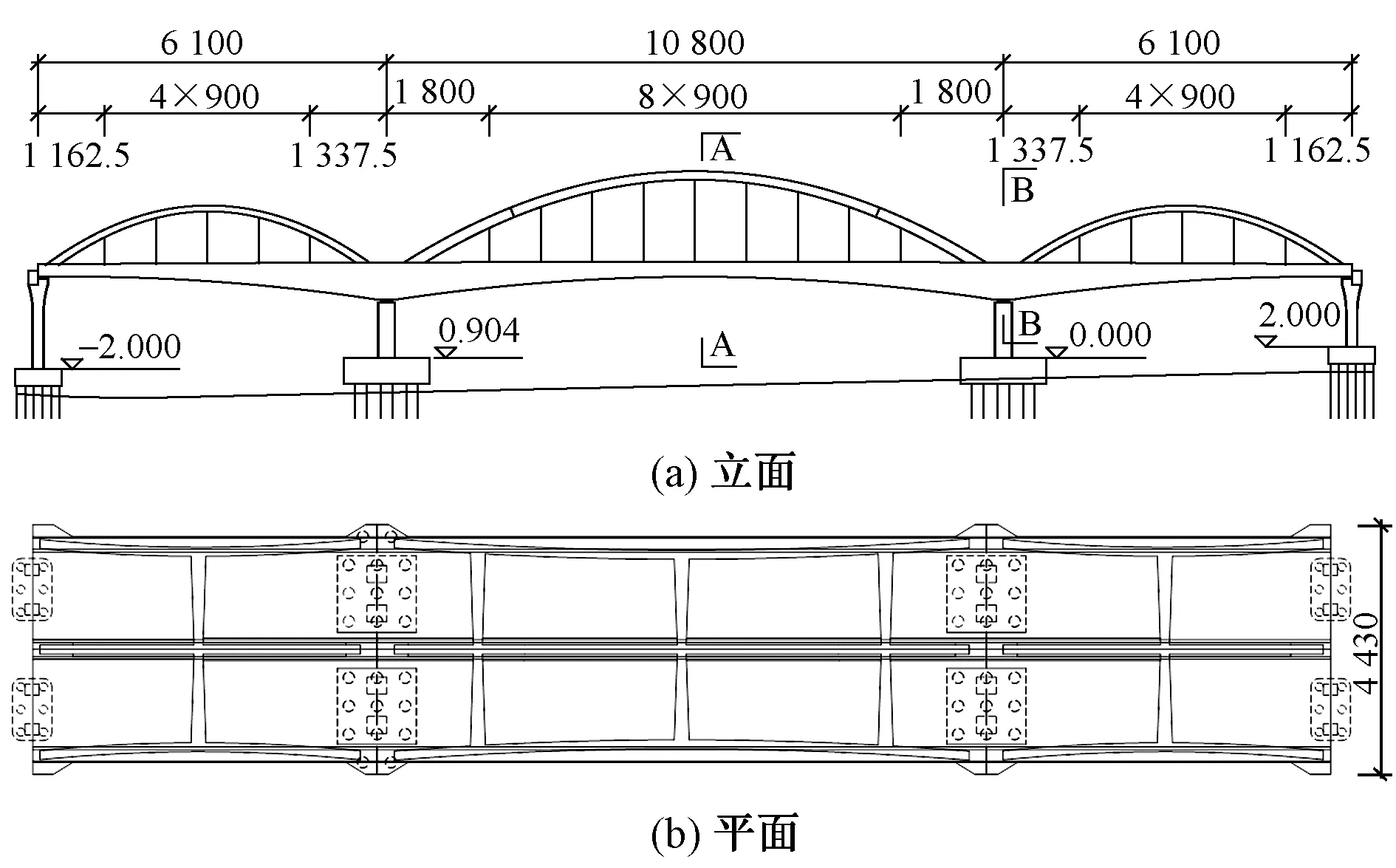
圖3 主橋立面及平面(單位：cm)

根據橋梁地勘報告，橋址場地為Ⅲ類場地。由橋址地震安全評價報告可知，橋址處于Ⅷ度設防區，橋址2000年重現期(E2水準)的地震峰值加速度為0.333 7g，潛在震源距30 km。摩擦擺支座的最大等效阻尼比為0.257(小于0.300)。有限元模型分析的基本振型為橋墩縱向彎曲，基本周期4.117 s，其質量參與系數為0.689。因此該橋沿縱向屬于規則結構，可以采用簡化算法分析橋梁結構的抗震性能。

2.2 結構抗震計算的簡化模型

為了方便簡化模型的建立，樁土效應通過現行規范中的M法計算樁周土的剛度，并作為彈簧施加在樁體上。根據沿墩頂順橋向作用的單位力，分別求得各橋墩的縱橋向抗推剛度，同時給出各橋墩的換算質量，見表1。

為了得到抗震性能優良、設計方案經濟的隔震支座參數，給出3種摩擦擺隔震支座設計方案，見表2。

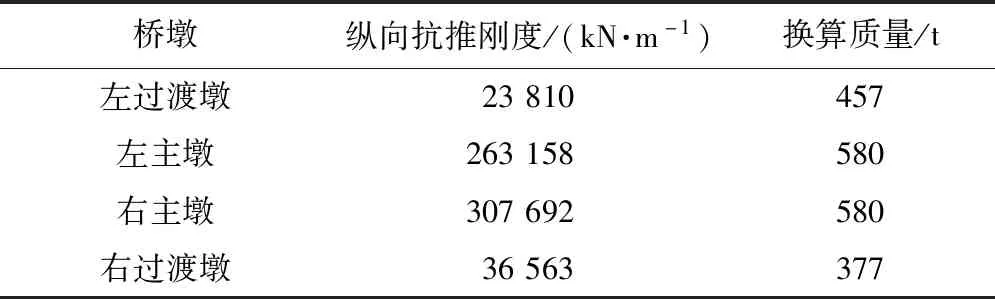
表1 橋墩縱橋向抗推剛度和換算質量

表2 等效單自由度系統摩擦擺隔震支座的設計方案

由于規范要求結構隔震后的基本周期應該是隔震前結構的2.5倍以上[9]，根據有限元模型計算得到未隔震結構的基本周期為1.74 s。由表2可知，當摩擦擺的半徑為5.85 m時隔震結構的基本周期為4.067 s，可以滿足要求。此時，結構的總體水平地震力Ehp=SMt=26 863 kN。根據橋墩剛度將水平地震力分配各個橋墩，可得到墩底的彎矩和豎向地震力。

根據橋梁結構設計參數建立SAP2000有限元模型進行非線性時程分析。摩擦擺支座參數取方案1，計算得到橋墩關鍵截面的地震響應，見表3。

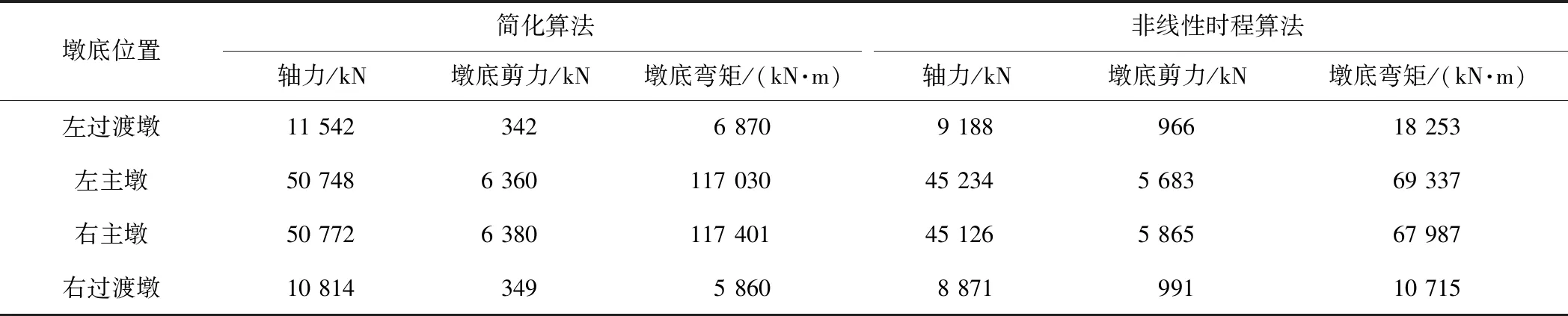
表3 罕遇地震作用下關鍵截面的地震響應

注：軸力以受壓為正。

由表3可知：簡化算法得到的左右主墩墩底剪力和彎矩大于非線性有限元的數值，可使得主墩的抗震設計偏于安全；而左右過渡墩因為計算過程中忽略了相鄰跨的影響，其剪力和彎矩簡化計算結果小于非線性有限元的分析結果，故采用簡化方法進行過渡墩抗震設計時，需采取有效措施適當增強其抗震能力。

罕遇地震作用下支座沿地震方向的位移響應見表4。簡化計算得到的支座位移設計值為0.52 m(參見表2)，對比表4發現支座的位移響應小于位移能力，說明支座設計是合理的。

表4 罕遇地震作用下支座沿地震方向的位移響應 m

3 結論

1)本文給出的簡化計算公式具有較高的精度，能夠較好地反映結構縱向的地震需求和考慮結構的基本特性，可以用于規則連續梁橋的初步抗震設計。

2)摩擦擺支座設計位移除了受自身參數(如擺的半徑、摩擦系數等)影響外，還需考慮橋梁墩剛度、基礎以及地震強度的影響。有限元模型計算的位移響應表明，支座的設計位移能力能夠滿足罕遇地震下的支座位移需求。