Ca-RG、Sr-RG與Hg-RG系統約化勢的理論研究

魏麗敏

(西安航空學院 理學院，西安 710077)

1 研究背景與主要內容

隨著激光技術、天體物理、新材料、光化學等重要學科的發展，分子間勢函數的研究引起了學術界越來越多的重視。雙原子分子勢函數是對雙原子分子結構的完全描述，在正確描述雙原子分子電子本征能量的同時，又可作為多原子分子勢能函數的多體項展式中的兩體項，它是研究多原子分子勢函數的基礎[1]。由兩個滿殼層原子(第IIA族堿土金屬原子Mg、Ca、Sr、Ba，第IIB族原子Zn、Cd、Hg以及第零族稀有氣體原子He、Ne、Ar、Kr、Xe)構成的雙原子體系，原子間由于瞬時偶極矩相互耦合而形成一個弱相互作用van der Waals鍵，組成分子的兩個原子基本上保持了原來的電子結構，它們基態的結合能很弱，這時應用量子力學從頭計算法，由兩個大物理量相減來算得如此弱的結合能會造成較大的誤差，而且應用量子力學來計算分子勢能函數很復雜又很費時。因此，很有必要尋求相對簡單而又可靠的勢模型對這類分子體系基態的結合能(van der Waals勢)進行研究。

1984年，Tang K T和Toennies J P教授從原子間相互作用的物理本質出發，提出了著名的描述van der Waals雙原子分子勢函數的Tang-Toennies勢模型[2](簡稱TT勢)。該模型很好地考慮了雙原子體系的庫侖排斥作用，電子交換作用，長程色散以及電子云重疊效應等，僅需五個參數就可以描述分子全程區域的勢能曲線，已成功的用于計算很多雙原子體系準確的相互作用勢[3-11]。對于Zn-RG(RG=He、Ne、Ar、Kr、Xe)系統各雙原子分子的基態van der Waals勢，能找到的相關實驗信息特別少，而理論計算結果之間也存在特別大的差距，所以我們很有必要探索是否能夠應用TT勢來描述各分子的勢能曲線。

在文獻[7]中，作者得到了這樣的結論： Sr2、Ca2和Hg2雙原子分子的約化勢曲線幾乎完全一致，但是不同于Ar2和Kr2的重合約化勢曲線；Sr-RG各分子的約化勢曲線一致。另外，在文獻[6]中，作者計算得到了Ca-RG系統各分子的TT勢能曲線，但是約化勢曲線未給出。在文獻[8]中，作者計算得到了Hg-RG系統各分子的TT勢能曲線，并且各分子的約化勢曲線幾乎完全重合。本文先驗證了Ca-RG系統各分子的TT約化勢曲線形狀相同，然后比較了Ca-RG、Sr-RG與Hg-RG各系統的約化勢曲線是否存在差別。如果不存在差距，那么我們就可以假設Zn-RG和Cd-RG系統各雙原子分子的van der Waals勢能曲線,也可以用TT勢模型描述并且滿足對應態原理，這些分子約化勢分別與Hg-RG系統各分子的約化勢共形，就可以從共形分子(約化勢形狀相同的分子)的約化勢參數出發，來得到Zn-RG和Cd-RG系統各分子的約化勢參數，并最后轉換為各分子的TT勢參數。這個想法的來源是約化勢要比實際的勢能相近得多，應用于約化勢參數的組合規則要更為準確。

2 計算方法

2.1 Tang-Toennies勢模型

Tang和Toennies教授在1984年提出了著名的描述van der Waals雙原子分子勢函數的Tang-Toennies勢模型[2]：

其中，A、b為排斥勢參數，C2n為色散系數，nmax一般情況下取nmax=5就足夠，更高階項對勢能的影響很小。勢模型中的參數都具有相應的物理意義，排斥勢參數A和b也不需要利用從頭算來得出，可由Re、De、C6、C8、C10的值反推得到相關結果[12]，其中Re為平衡間距，De為勢阱深度。TT勢的精確度較高，是一種非常重要的雙原子分子勢函數模型，也可以推廣用于描述原子與離子XY+間的勢能函數[13]。直到1991年，Tang和Toennies教授仍在對TT勢模型作進一步的改進和完善[14]。 TT勢函數是一個解析式，各階導數都存在，因此可以方便地用于需要解析擴展到復平面的理論。

2.2 對應態原理

對應態原理最早是由van der Waals在1880年提出的，他分別用體積、溫度和壓力的值除以它們各自的臨界值，得到了一個具有普遍性的狀態方程。由于一個體系的狀態可以由上述三個參數中的任意兩個來描述，對應態原理表示所有的物質都遵循相同的由兩個約化參數形式給出的狀態方程[15]，是一種非常實用的物理研究方法[16]。

1938年，De Boer和Micherls[17]以及稍晚的Pitzer[18]給出這樣的結論：如果以V(R)=DeU(R/Re)的勢函數形式來描述分子勢能時，是滿足對應態原理的。其中，U(x)為勢能的約化形式，R為核間距，Re為平衡間距，De為勢阱深度。例如，大家熟知的Lennard-Jones(12-6)勢的約化形式為U(x)=x-12-2x-6。這樣，兩種不同分子各自的相互作用勢可以用不同的Re和De值由LJ(12-6)勢模型給出，滿足對應態原理，也可以表述為這兩種分子的約化勢是共形的。后來，通過對精確的實驗數據分析，發現并不是所有的物質的勢能曲線都滿足對應態原理。但是，在高精度范圍內，所有稀有氣體同核雙原子間的勢能約化形式是一致的，只是這種約化形式不能用先前使用的簡單勢函數，如LJ(12-6)或Morse勢來描述。

TT勢模型能精確地描述稀有氣體21種同核及異核雙原子間的相互作用勢[4]，而且結果還證明這些分子滿足對應態原理，它們的約化勢相互共形。后來，TT勢被用于描述Ca-RG[6]、Sr-RG[7]和Hg-RG[8]系統各分子的van der Waals勢，并且Sr-RG與Hg-RG各系統的約化勢分別共形。

2.3 Tang-Toennies約化勢

在TT勢模型中，令：

x=R/Re

(2)

U(x)=V(Rex)/De

(3)

則勢函數的約化形式為：

其中：

b*=bRe

(6)

在勢阱位置，即R=Re(x=1)處，約化勢滿足以下條件：

U(x)=-1

(8)

3 結果與分析

研究者已對Ca-RG、Sr-RG與Hg-RG系統各分子基態的van der Waals勢作了詳細的研究[6-8]，各分子的TT勢參數是已知的，本次計算以這些分子的TT勢參數作為計算的基礎數據，并列于本文的表1～表3中。

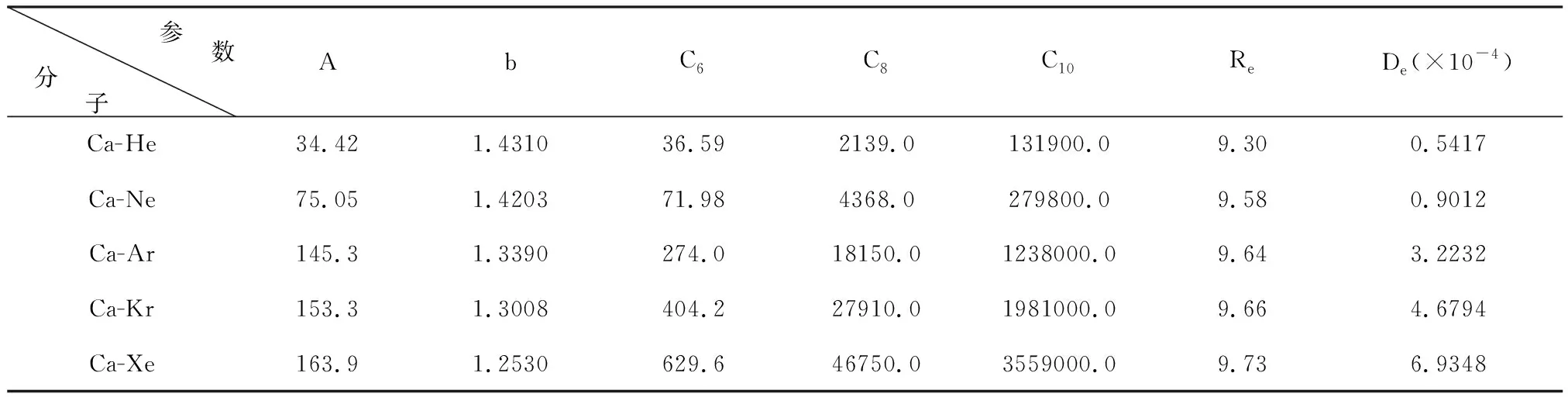
表1 Ca-RG系統各分子的TT勢參數 單位：a.u.

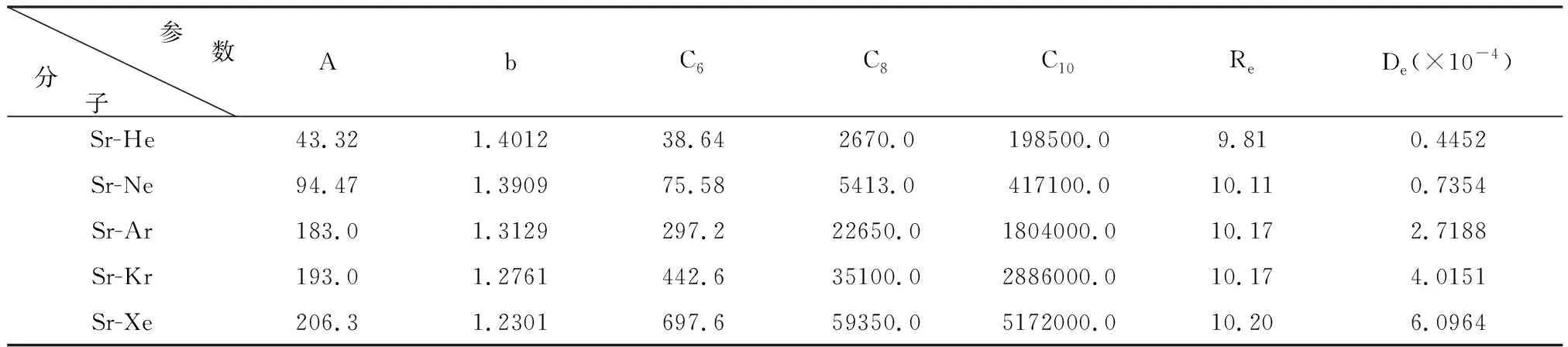
表2 Sr-RG系統各分子的TT勢參數 單位：a.u.

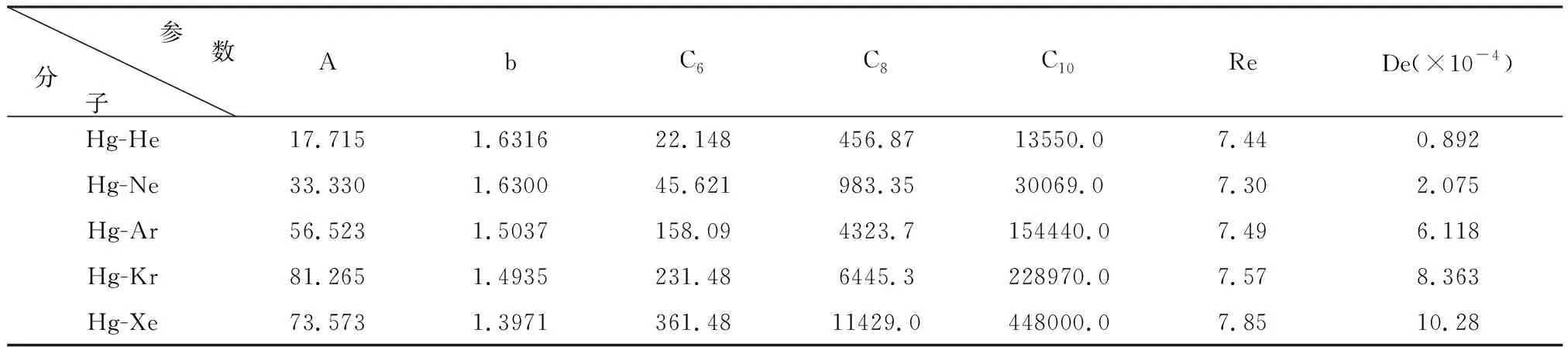
表3 Hg-RG系統各分子的TT勢參數 單位：a.u.

從表1～表3中可以看到，各個系統中各雙原子分子的勢能參數差距相當地大，比如說Ca-RG系統中，Ca-He 與Ca-Xe分子的色散系數C6相差16倍之多。表4中列出的是通過(5)～(7)式計算得到的Ca-RG系統各分子的約化勢參數，從此表中可以看到Ca-He、Ca-Ne、Ca-Ar、Ca-Kr、Ca-Xe這五種異核雙原子分子各對應的約化勢參數都基本上相同，比表1中的勢參數要彼此接近的多很多，與Ca-He 與Ca-Xe分子的約化色散系數C6*幾乎完全一致。盡管它們不是完全相同，但是在排斥區的微小差距可以由吸引區的差別補償，所以作U(x)-x圖時，從圖1中可以看到，這五條約化勢曲線是完全重疊在一起的，這種勢能曲線的不變性并不是使用相同勢模型的結果。Sr-RG與Hg-RG系統各分子基態的TT約化勢在這里就不再給出，結果與Ca-RG系統的情況一致，各系統的約化勢分別重合在一起。

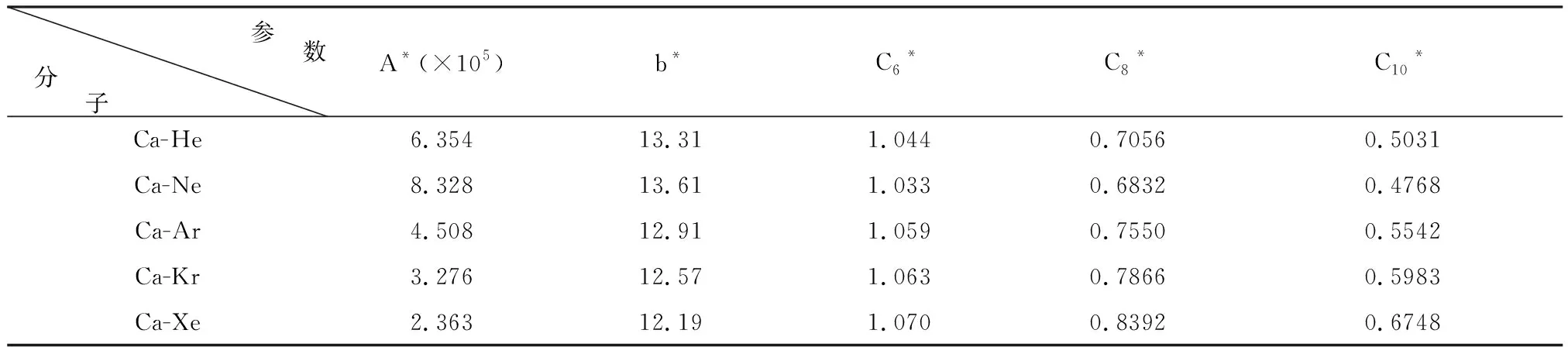
表4 Ca-RG系統各分子的TT約化勢參數

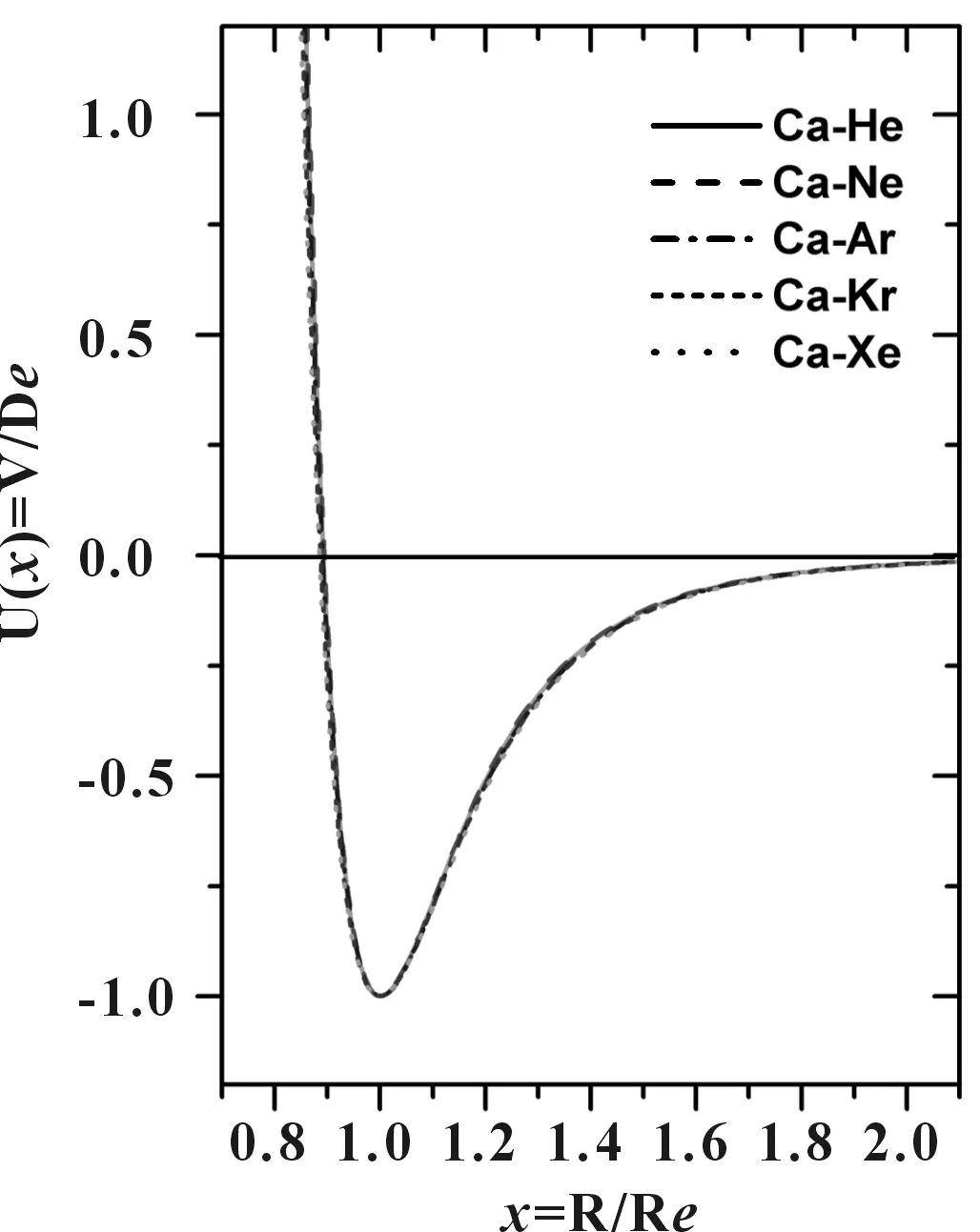
圖1 Ca-RG系統各分子的約化勢曲線

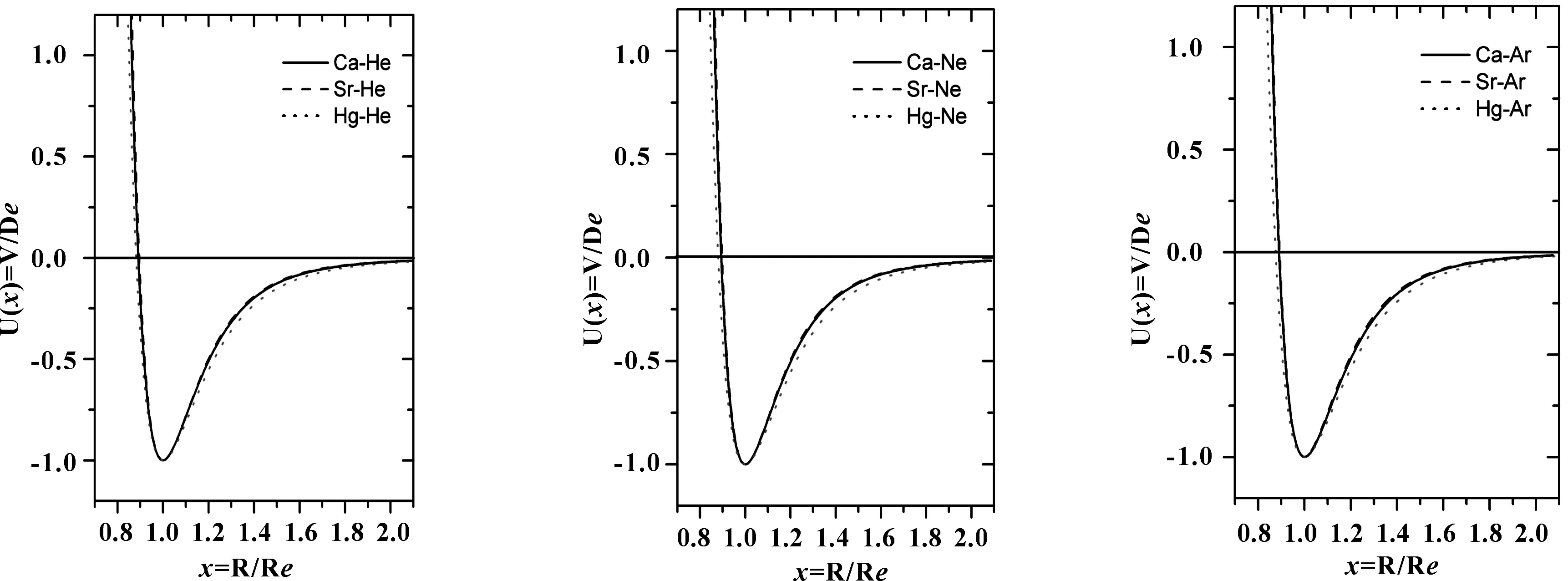
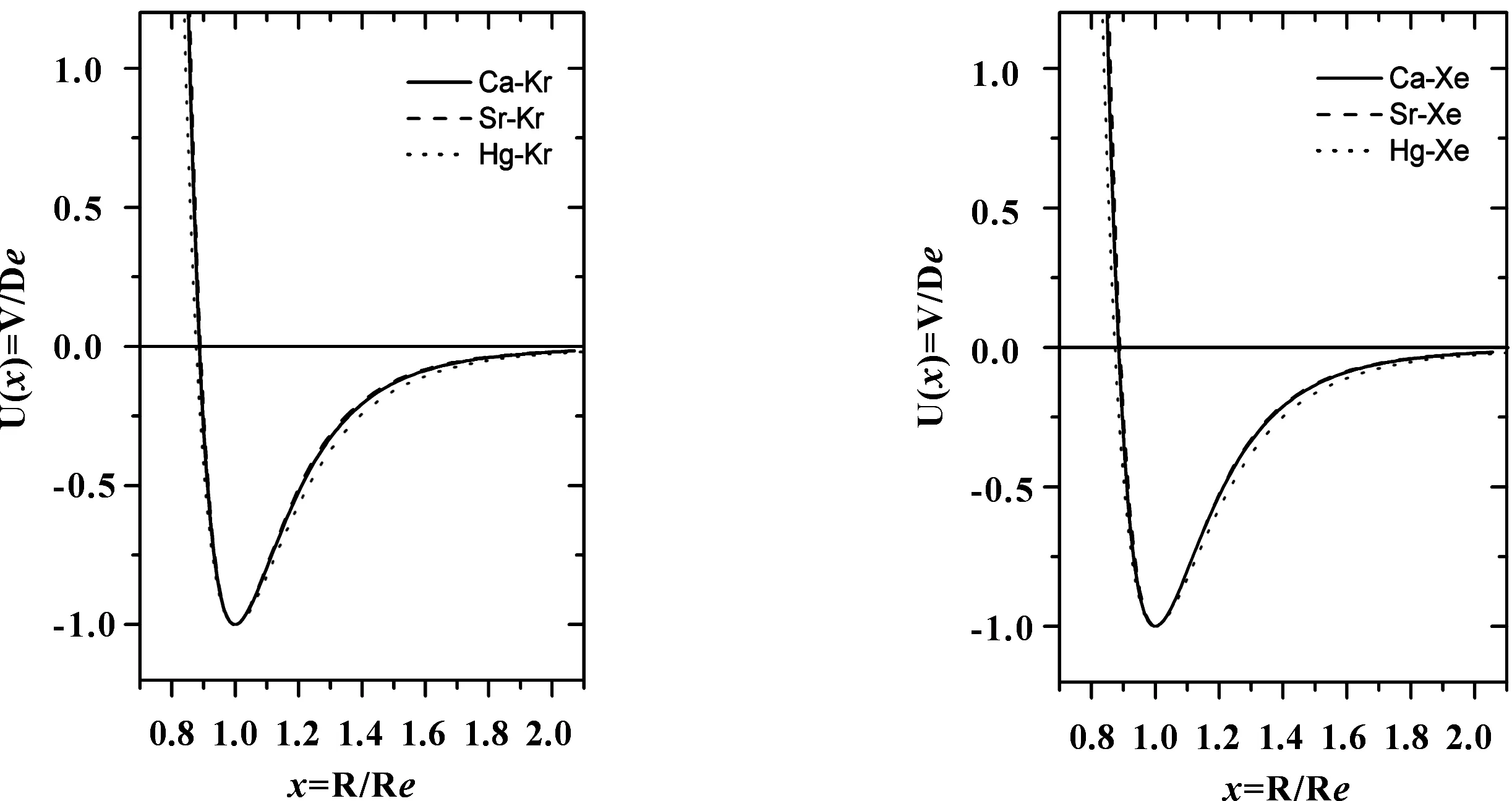
為了比較這三個系統各自重合的約化勢曲線有何區別，本文分別給出了它們之間的比較圖，為了清晰可辨，分別畫在了圖2中的五幅圖中。從圖2中可以看到，雖然是不同的雙原子分子的約化勢曲線比較圖，但這五幅圖的曲線形狀幾乎一模一樣，Ca-RG與Sr-RG系統的約化勢曲線完全重合，而Sr-RG系統各分子的約化勢曲線與Ca-RG、Sr-RG系統對應分子的約化勢曲線稍有差別，在長程區范圍要稍微深一些。

(a) (b) (c)

(d) (e)

圖2Ca-RG、Sr-RG和Hg-RG系統的約化勢曲線比較

Ca與Sr原子同屬于第IIA族，而Zn、Cd、Hg原子同屬于第IIB族，既然Ca-RG和Sr-RG系統各分子的TT約化勢曲線完全吻合，我們假設Zn-RG和Cd-RG系統各雙原子分子的van der Waals勢能曲線也可以用TT勢模型描述并且滿足對應態原理，那么這些分子約化勢分別與Hg-RG系統各分子的約化勢共形來構建Zn-RG和Cd-RG系統各分子勢函數的計算方法是合理可行的。

本文的計算結果表明，對應態原理的實用價值，同時也期望本文的研究結果能夠提供有效的關于更多體系的異核相互作用勢的計算方法，對今后勢模型的研究以及組合規則的建立起到一定的指導意義。