基于PCA-WNN模型的油田回注水管道腐蝕速率預測
于淼
中國石油新疆油田公司風城油田作業區
目前,我國大多數油田都將采出水進行處理后回注到地層中,以此補充地層能量,同時又可以減輕采出水排放所帶來的環境污染問題[1]。但是由于采出水中含有大量的腐蝕性成分,極容易給回注水管道造成腐蝕,當回注水管道腐蝕嚴重時,可能會導致回注水泄漏,從而給外界環境造成污染[2]。因此,對回注水管道的腐蝕問題進行深入研究十分重要。
國內外專家對油田回注水管道的腐蝕問題進行了多方面的研究。挪威石油公司提出了回注水管道腐蝕速率預測的Norsok經驗模型,但是由于該模型基于實驗室實驗結果,并沒有考慮油田現場條件,且模型較為簡單,因此腐蝕速率計算結果誤差較大;王俊奇等人[3]采用了灰色關聯度的方法對影響回注水管道腐蝕速率的相關因素進行了排序,并將排序結果與實際結果進行對比,指明了回注水管道腐蝕速率的主要影響因素,但其并沒有對回注水管道的腐蝕速率進行預測;游琪[4]采用實驗的方法,研究了溫度、流速等因素對回注水管道的腐蝕影響,并對目前常見的回注水管道緩蝕劑進行了評價,但其也未對回注水管道的腐蝕速率進行有效預測;王亮[5]采用BP神經網絡模型對回注水管道腐蝕速率進行了預測,但是由于其考慮的腐蝕速率影響因素不夠全面,所以預測結果相對較差。
通過以上分析可以發現,目前大多數研究成果都集中于回注水管道腐蝕速率影響因素分析方面,少部分研究成果對腐蝕速率進行了預測,但是由于影響因素分析不夠全面,所以預測結果并不準確。針對油田回注水管道的腐蝕速率問題,本文首先對回注水管道腐蝕速率的影響因素進行深入分析,并使用PCA算法對影響因素進行優選,然后使用WNN算法對腐蝕速率進行預測,從而為油田回注水管道的安全運行奠定基礎。
1 腐蝕速率影響因素分析
目前,我國大多數回注水管道都采用涂層防腐技術以降低管道腐蝕速率,但是回注水管道使用一段時間后,涂層會出現一定的破損。涂層處于完好狀態時,管道的腐蝕速率相對較低;當涂層處于破損狀態時,管道的腐蝕速率將大大提高。在本次研究中,由于數學模型不能用文字表示,所以在數學模型輸入時,將管道涂層完好狀態用“0”表示,將管道涂層破損狀態用“1”表示。目前的研究結果顯示,隨著管道內溫度的增加,回注水管道的腐蝕速率也將增加,當管道內的溫度升高到80℃左右時,回注水管道的腐蝕速率將不再變化[6-7]。一般情況下,回注水壓力會對管道的腐蝕速率產生影響,隨著回注水壓力的持續增大,管道的腐蝕速率也將持續增大[8]。回注水流速會對回注水管道腐蝕速率產生較為嚴重的影響,目前的實驗結果顯示,當回注水的流速從0.7 m/s增加到1.4 m/s時,管道的腐蝕速率將增加5倍[9]。回注水中含有大量的CO2,CO2與水反應將產生碳酸,碳酸會對回注水管道產生直接腐蝕。H2S會在水中發生電離,并與其他成分作用產生硫化物,硫化物也將會對回注水管道產生腐蝕,回注水中硫化物的含量越高,則回注水管道的腐蝕速率將越大[10]。溶解氧的存在為回注水管道腐蝕提供了基礎條件,目前的研究結果顯示,當回注水中溶解氧的質量濃度在1 mg/L左右時,回注水管道極易遭受腐蝕。pH值也是造成回注水管道腐蝕的主要原因之一,目前的研究結果顯示,當pH值小于4時,回注水將呈現強酸性,管道表面的氧化物也會被溶解[11]。一般情況下,回注水管道內存在的SRB(氧化還原菌)繁殖能力較強,會對管道產生直接腐蝕[12]。
根據以上分析結果,回注水管道腐蝕速率將受到管道涂層完好性,回注水溫度、壓力、流速,CO2及H2S含量,溶解氧含量,pH值以及SRB含量的影響。在對回注水管道腐蝕速率進行預測時,影響因素越多,則模型的學習預測速度越高,需要通過降維的方法減少影響因素的數量。但是減少影響因素的數量不能對最終的預測結果產生影響,為此,采用PCA(主成分分析)算法對回注水管道腐蝕速率的影響因素進行降維處理。
2 腐蝕速率預測模型構建
2.1 數據來源
本次研究所采用的數據來源于國內某油田,該油田采出液含水率高達90%,必須對其進行回注處理。經過多年檢測,共統計到45組回注水管道腐蝕速率及影響因素數據,部分數據如表1所示。在本次研究中,將其40組數據作為模型的訓練樣本,將剩余的5組數據作為模型的預測樣本,并將預測結果與實際腐蝕速率進行對比。
2.2 PCA算法
PCA算法是一種最常見的數據降維算法[13]。假設回注水管道影響因素數據組合成的矩陣為X,其中,矩陣 X的列向量 Xk=(x1k,x2k,…,xnk)T即為某一項影響因素的數據,回注水管道的腐蝕速率就可以通過xk來描述,xk的協方差矩陣計算公式為
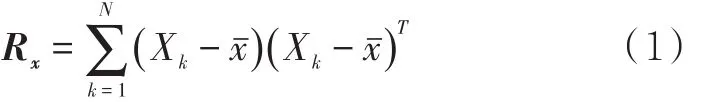
式中:N為模型中訓練樣本的數量; xˉ為各個影響因素的均值。 xˉ為

然后即可求解協方差矩陣的特征值和特征向量,求解公式為

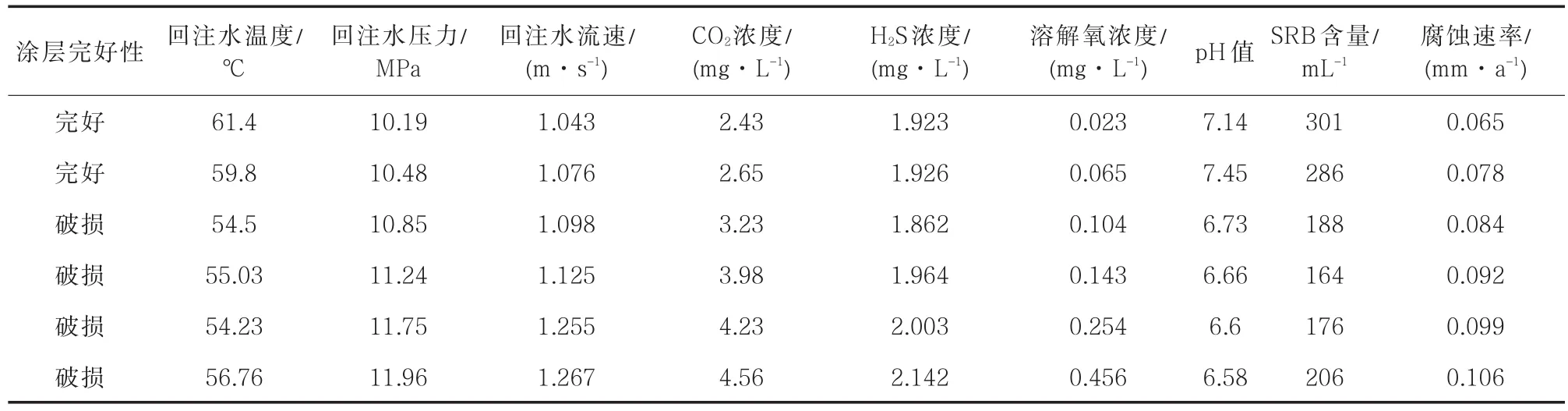
表1 部分回注水管道腐蝕影響因素及腐蝕速率數據Tab.1 Corrosion influencing factor and rate data of some refilled water pipelines
式中:λi為協方差矩陣Rx的特征值;qi為協方差矩陣Rx的特征向量。
此時樣本xi在投影到特征向量qi中的主成分為

假設前m個主成分用 y1,y2,…,ym表示,則這些主成分對腐蝕速率的累計貢獻率為

一般情況下,當某些因素的累計貢獻率超過85%時,即可使用這些因素代替所有影響因素進行預測[14]。在本次研究中,為了保障腐蝕速率預測結果的準確度,將累計貢獻率超過98%的因素作為回注水管道腐蝕速率的主要影響因素來進行下一步的預測工作。
2.3 WNN算法
WNN(小波神經網絡)算法是一種以BP神經網絡為基礎發展而來的預測算法[15]。該種算法的隱含層傳遞函數為小波函數,在使用的過程中,信號將向前傳播,同時誤差將向后傳播[16]。其基本原理:假設 X1,X2,…,Xn為該算法的輸入參數,Y1,Y2,…,Yn為該算法的預測結果, ωij和 ωjk為該算法的權值。在輸入參數序列xi( )i=1,2,…,k以后,隱含層將對其進行計算,計算公式為
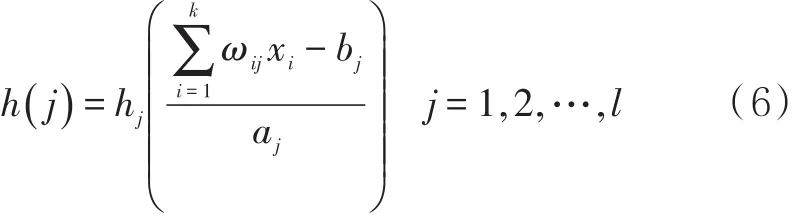
式中:h(j)為隱含層中第 j個節點的計算值; ωij為輸入層與隱含層之間的連接權值;hj為小波基函數;bj為小波基函數的平移因子,aj為小波基函數的伸縮因子。
將采用Morlet函數作為小波基函數,該種函數的數學表達式為
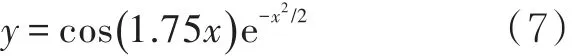
該種算法輸出層的預測結果為
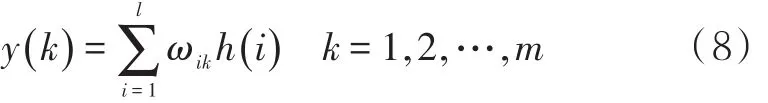
式中:y(k)為預測結果;l為隱含層的節點數量;m為輸出層的節點數量;ωik為隱含層與輸出層之間的連接權值;h(i)為隱含層第i個節點的輸出值。
2.4 PCA-WNN模型構建
首先將回注水管道腐蝕速率及其影響因素的數值輸入到PCA算法中,對其進行降維處理。根據降維結果,將45組回注水管道腐蝕速率的實際數據隨機分為兩類,一類作為訓練樣本,包含40組數據,另一類作為預測樣本,包含5組數據,將其輸入到WNN算法中進行預測,并將預測結果與實際腐蝕速率進行對比,計算預測結果的平均絕對誤差。PCA-WNN模型結構如圖1所示。
3 腐蝕速率預測結果分析
3.1 PCA處理結果分析
在Matlab軟件中編寫PCA算法,根據油田回注水管道腐蝕速率影響因素分析結果,將管道涂層完好性,回注水溫度、壓力、流速,CO2及H2S含量,溶解氧含量,pH值以及SRB含量等因素輸入到PCA算法中,PCA處理結果如表2所示。從表2可以看出,涂層完好性、CO2含量對回注水管道腐蝕速率的影響最大,回注水管道壓力對回注水管道腐蝕速率的影響最小,這也從側面證明了上文的分析結果;同時,涂層完好性,回注水溫度,流速,CO2及H2S含量,溶解氧含量,pH值以及SRB含量等8種影響因素對腐蝕速率的累計貢獻率超過了98%,因此可以忽略回注水管道壓力的影響,并以涂層完好性,回注水溫度、流速,CO2及H2S含量、溶解氧含量,pH值以及SRB含量等8種影響因素代替所有影響因素進行下一步的腐蝕速率預測工作。
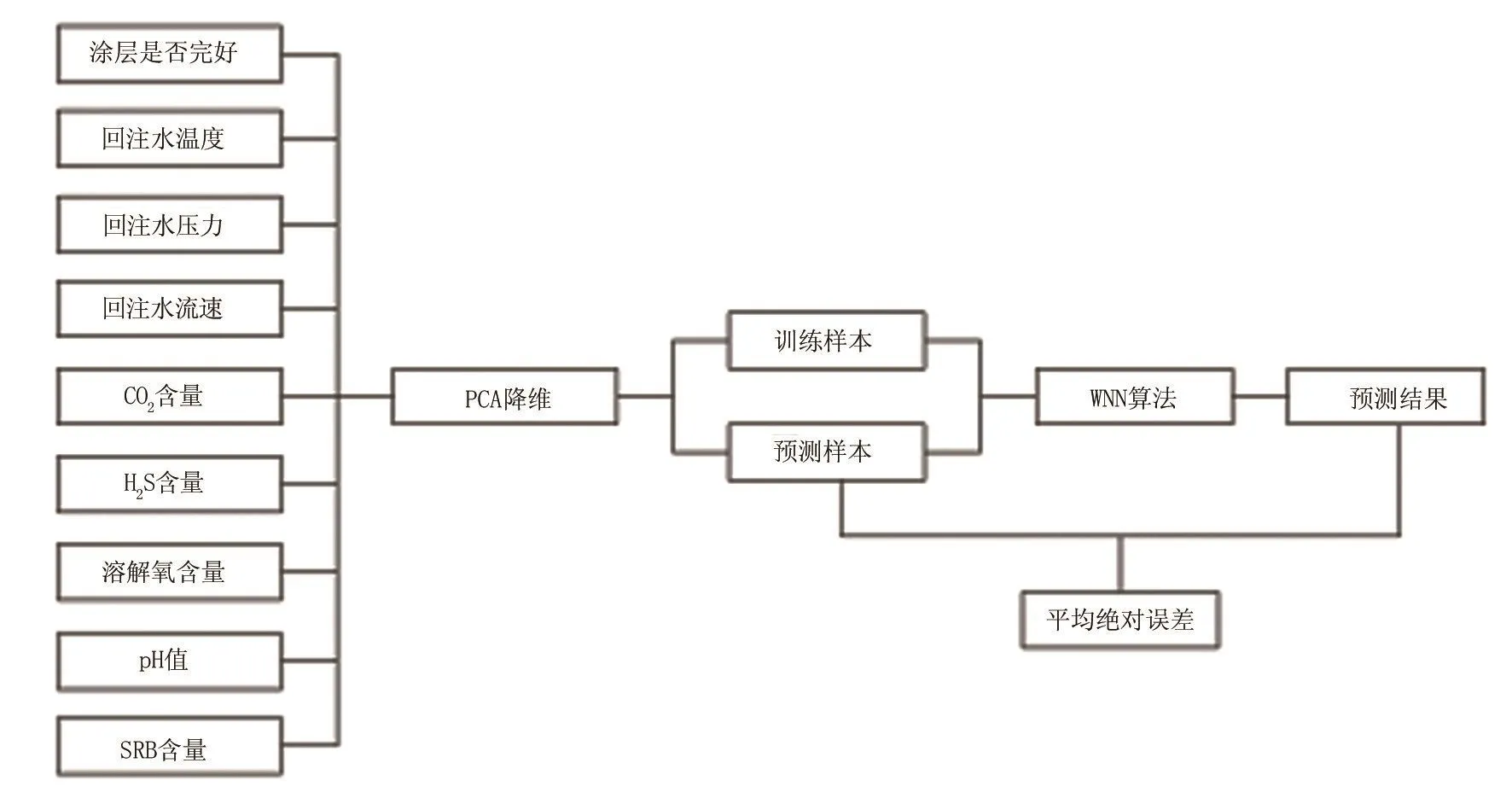
圖1 PCA-WNN模型結構Fig.1 PCA-WNN model structure

表2 PCA處理結果Tab.2 PCA processing results
3.2 模型預測結果分析
在Matlab軟件中分別編寫WNN算法、BP神經網絡算法以及GM(1,m)算法,根據PCA降維結果,把涂層完好性,回注水溫度、流速,CO2及H2S含量,溶解氧含量,pH值以及SRB含量作為回注水管道腐蝕速率的影響因素,將隨機選取的40組實際數據輸入到這3種算法中進行學習,對剩余5組數據進行預測,計算每種預測算法的平均絕對誤差,并統計每種算法的數據訓練時間。3種預測模型的預測結果如圖2所示,預測結果的誤差情況如圖3所示,預測結果的平均絕對誤差及數據訓練時間如表3所示。可以看出,PCA-WNN模型的預測結果與實際回注水管道腐蝕速率基本相同,預測結果的最大誤差不超過3%,平均絕對誤差僅為1.35%,且模型的數據訓練時間最短;PCA-BP神經網絡預測結果誤差變動情況最大,且平均絕對誤差高達10.96%;PCA-GM(1,m)模型的預測誤差雖然低于PCA-BP神經網絡,但是模型的數據訓練時間最長。可見PCA-WNN模型適用于油田回注水管道腐蝕速率預測。
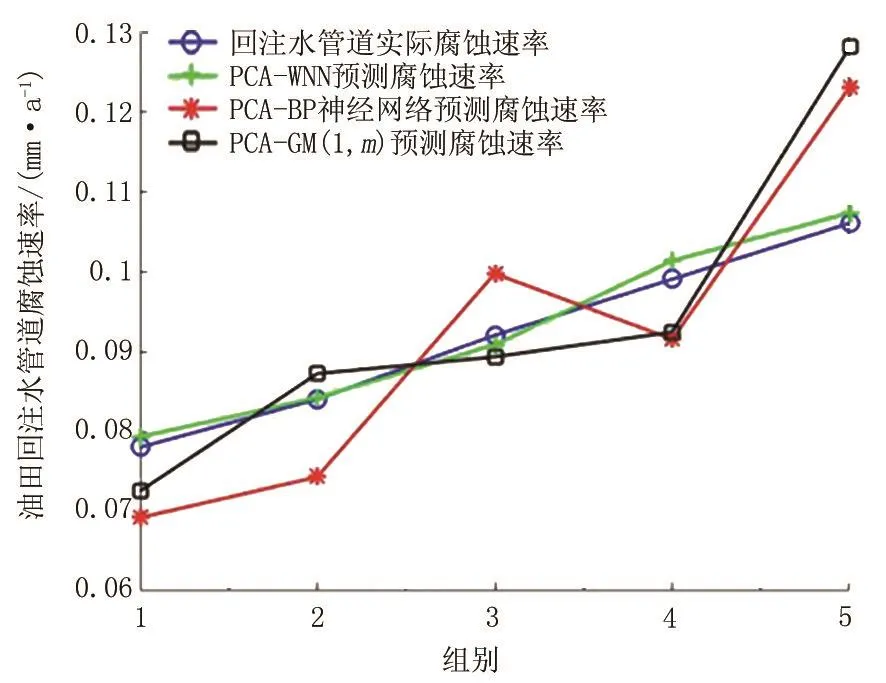
圖2 常見模型預測結果Fig.2 Common model prediction results
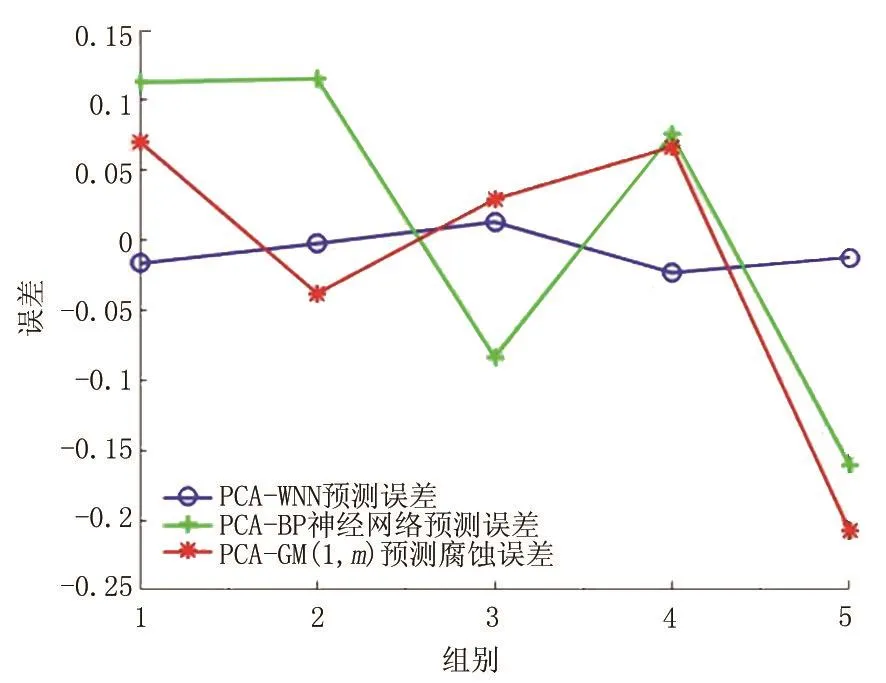
圖3 常見模型預測結果誤差Fig.3 Error of common model prediction results
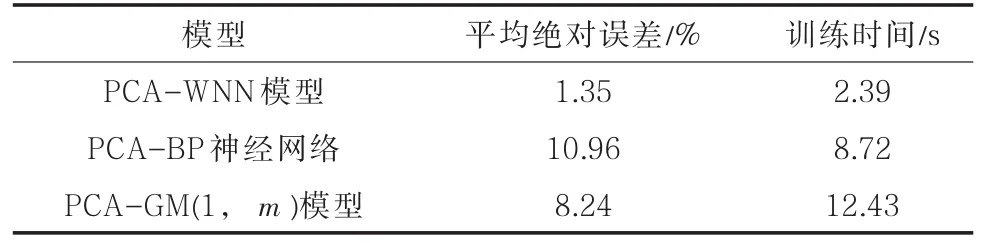
表3 常見模型預測平均絕對誤差及訓練時間Tab.3 Mean absolute error and training time of common model prediction
4 結論
(1)盡管涂層完好性,回注水溫度、壓力、流速,CO2及H2S含量,溶解氧含量,pH值以及SRB含量都會對管道腐蝕速率產生影響,但是影響效果各不相同,其中涂層完好性、CO2含量對管道腐蝕速率的影響最大,而回注水壓力對管道腐蝕速率的影響最小。
(2)根據預測結果顯示,PCA-WNN模型的預測結果與實際回注水管道腐蝕速率基本相同,預測結果的最大誤差不超過3%,平均絕對誤差僅為1.35%,數據訓練時間僅為2.39 s,預測誤差和數據訓練時間均小于其他模型,因此PCA-WNN模型適用于油田回注水管道腐蝕速率預測。

