金屬材料聲發(fā)射信號傳播的聲阻抗特性研究

毛漢穎, 劉 婷, 范健文, 毛漢領

(1.廣西科技大學 機械與交通工程學院，廣西 柳州 545006；2.中山火炬職業(yè)技術學院 裝備制造系，廣東 中山 528437；3.廣西大學 機械工程學院，南寧 530004)

聲發(fā)射信號是材料變形或破壞時應變能釋放而產(chǎn)生的瞬態(tài)彈性波。因為聲發(fā)射信號本身有著動態(tài)性、敏感性、整體性和及時性等優(yōu)點，近年來在缺陷源定位和提取故障信息等方面得到了廣泛應用，但對其傳播特性的研究還較少。

可采用數(shù)值仿真和實驗手段來研究聲發(fā)射彈性波的傳播特性。目前主要采用MATLAB、ANSYS/LS-DYNA和Virtual.Lab Acoustics 等軟件來進行數(shù)值仿真研究，如郝建軍等[1]通過MATLAB研究了大地介質(zhì)中彈性波入射角度對于傳播和衰減的影響；邵忍平等[2]用ANSYS和MATLAB數(shù)值模擬分析了不同齒輪裂紋及位置產(chǎn)生聲發(fā)射的輻射聲場特性；吳先梅等[3]應用Virtual. Lab Acoustics研究了瑞利波在不同半徑圓柱表面的傳播波速曲線。數(shù)值仿真主要是針對特殊波型在簡單結構中的傳播仿真，深入的傳播特性仿真還很局限。實驗主要對不同材料不同結構在不同條件下聲發(fā)射信號的傳播特性開展研究。郭福平[4]重點對7種不同直徑、3種不同長度的波導桿中聲發(fā)射信號的傳播特性進行了實驗研究。毛漢穎等[5]采用共振理論設計研制了不同材料、不同諧振長度的諧振傳導桿，試驗表明其對聲發(fā)射信號具有幅值放大和帶通濾波功能。毛漢穎等[6]還研究了聲發(fā)射信號經(jīng)過螺栓緊固聯(lián)接面、大小界面接合面、焊接面、法蘭連接面等四組典型接合界面?zhèn)鞑サ膫鬏斔p特性。肖儼衍等[7]建立了聲發(fā)射信號在三種常見軸(如光軸、階梯軸、階梯退刀槽軸) 中的傳播模型，研究了其對聲發(fā)射信號傳播的影響。王向紅等[8]研究裂紋長度和裂紋位置對聲發(fā)射信號傳播特性的影響。Mba等[9]研究了汽輪機轉子碰摩時產(chǎn)生聲發(fā)射信號通過軸承、軸承座傳播，在軸承座外面安裝傳感器檢測的問題，重點討論了聲發(fā)射信號經(jīng)過長距離、接觸界面的衰減特性。Dahmene等[10]針對在低溫、高溫下的接觸檢測采用波導桿傳播聲發(fā)射擊信號，認波導桿長度不會改變信號的頻率，只是信號的波形稍有改變、信號的幅值變小。Elasha等[11]采用自適應濾波、峭度和包絡分析從行星齒輪變速箱強背景噪聲中提取軸承故障產(chǎn)生的聲發(fā)射和振動信號，對比分析認為經(jīng)過雜路徑傳播后聲發(fā)射比振動信號能更好地辨識早期的故障。

目前計算聲阻抗的方法一般是超聲脈沖回波法，它是通過對材料進行超聲回波信號測量進而求取聲波反射系數(shù)，然后根據(jù)反射系數(shù)來確定聲阻抗。李功燕[12]對提高超聲波回波信號的信噪比、剔除多重反射等問題進行了系統(tǒng)的研究，提高了重建估算聲阻抗的精確性和可靠性；陳玉喜等[13]設計了一種通過待測試件表面超聲反射回波計算得到試件表面的聲阻抗值的聲阻抗測量方法；楊克己[14]實現(xiàn)了一種采用DSP和ARM芯片作為中心測控單元的嵌入式便攜聲阻抗重建系統(tǒng)。

目前直接用聲發(fā)射信號估計聲阻抗方面的研究較少，聲阻抗作為最基本、直觀的表征材料動態(tài)力學特性重要的物理量，借助它來研究聲發(fā)射信號在材料中的傳播特性，應該值得嘗試。

本文擬利用聲阻抗來研究聲發(fā)射信號在金屬材料中的傳播，從解波動方程問題的基本方程式以及波譜系數(shù)轉換公式來反演介質(zhì)的聲阻抗比值，得到聲阻抗比值與材料損傷過程及損傷趨勢變化的關系；通過實驗驗證聲阻抗可以通過斷鉛聲發(fā)射來估算聲阻抗比值，并檢測服役后金屬材料的受損傷程度。

1 斷鉛聲發(fā)射估計聲阻抗的方法

1.1 正演問題

聲發(fā)射波作為一種機械波，其輻射、傳播等一系列物理過程完全遵循聲波的規(guī)律，所以，本文采用聲波的相關理論來研究聲發(fā)射。由于實際情況中，金屬材料較常受到往復加卸載的情況導致其受損后材料不再均勻，致使其存在由多層聲阻抗大小不同組成的界面，在各層界面會發(fā)生多次透射波和反射波的疊加，導致波形的畸變，故將它視為分層介質(zhì)處理。而在頻域分析中，不論在待測介質(zhì)層中發(fā)生多少次透射波和反射波的疊加，都可將其視為一個右行波和一個左行波在數(shù)值計算中實現(xiàn)。

如圖1所示，用L、R表示介質(zhì)層中的左、右行波的波幅系數(shù)，下標表示行波所在的介質(zhì)層數(shù)，下面以圖1中第k層和第k+1層之間的傳遞為例，說明左右行波的波幅系數(shù)的轉換。

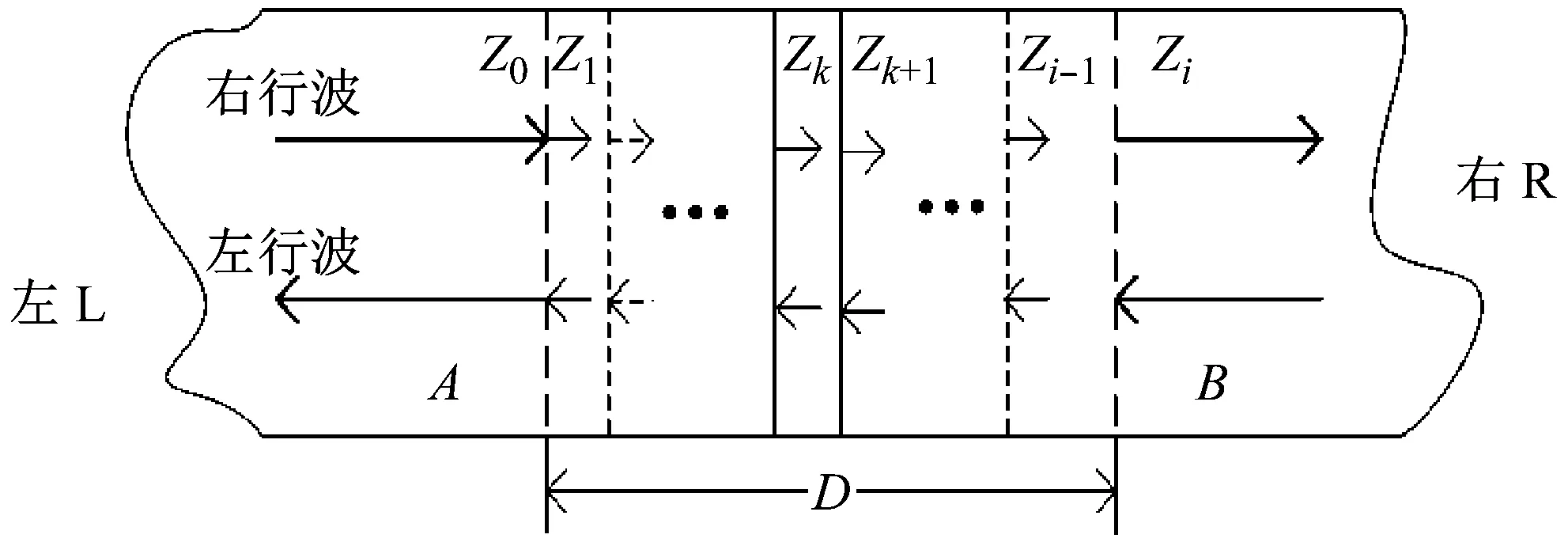
圖1 左右行波傳播示意圖

設第n層中，左行波和右行波的總位移為

(1)

n+1層中的左、右行波的位移為

(2)

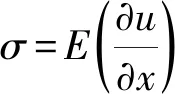
(3)

式(3)給出的第n層和第n+1層波幅系數(shù)轉換關系時，左右兩層采用的是同一坐標系。如果采用每一層左側為原點構造局部坐標系來描述該層內(nèi)的波動，第n層和第n+1層波幅系數(shù)的轉換關系可寫成如下形式

Hn+1=TnHn,n=1,2,…,N-1

(4)

這里第n層的波幅矢量Hn為

(5)

相鄰層間的轉換矩陣Tn為

(6)

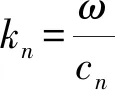
由遞推公式(4)可以得到最左側和任一層之間的波幅系數(shù)轉換關系

(7)

(8)

由此看出，若已知初始位置入射波波幅矢量，則由式(4)～式(8)可得到任意一層中的波的響應。

1.2 反演問題

實現(xiàn)反演的方法有很多，本文采用通過正演實現(xiàn)過程的反演方法來解決，即利用輸入波形的正演關系得到的輸出結果波形對實際測得的聲發(fā)射輸出波形不斷地進行擬合，從而反演介質(zhì)層中的聲阻抗比值。聲阻抗反演流程圖,如圖2所示。

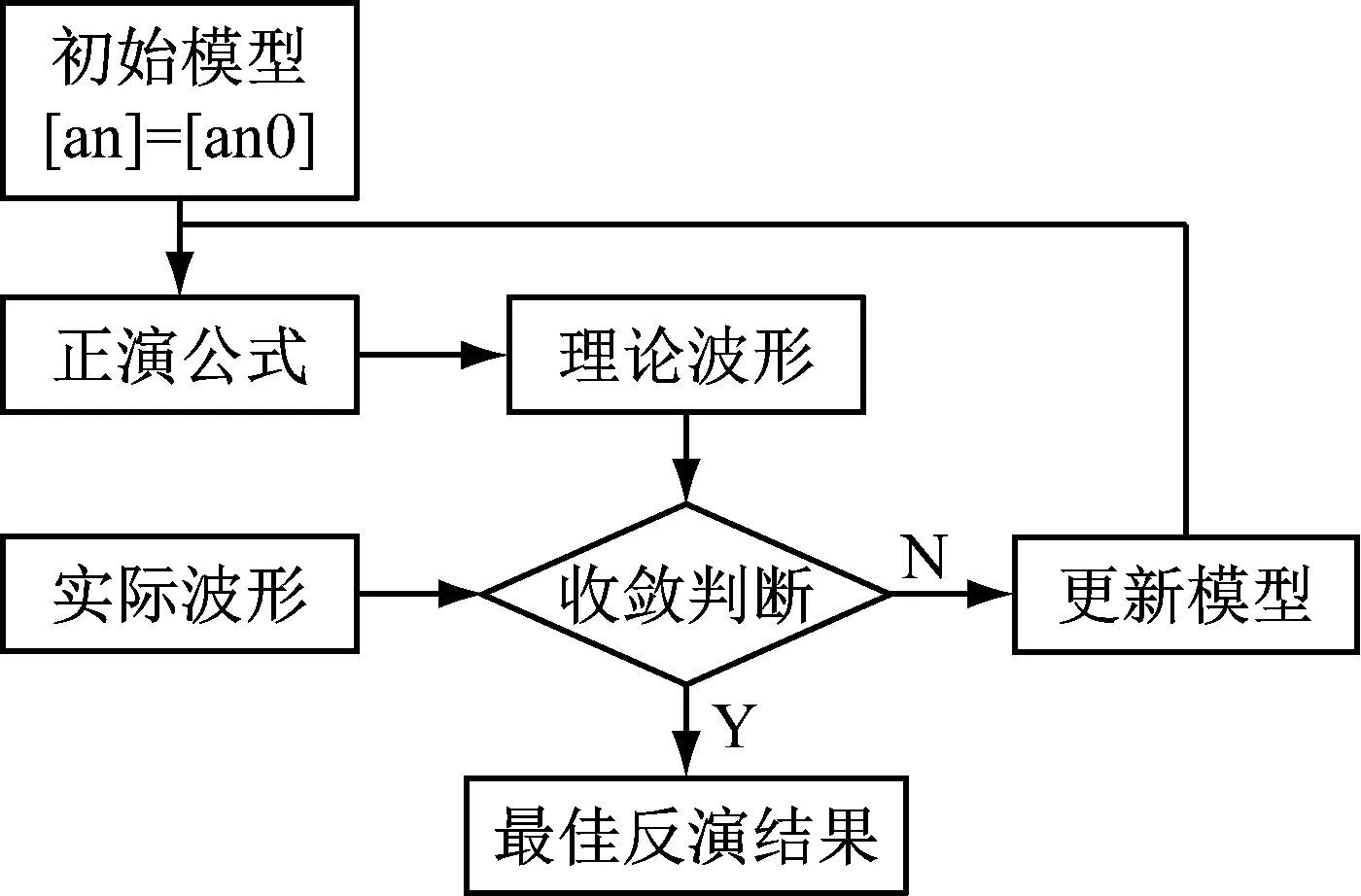
圖2 聲阻抗反演流程圖

在本文中，利用反演思路可簡單描述為：

在反演時，我們已知分別在如圖1所示的輸入端A、輸出端B接收到的輸入、輸出聲發(fā)射信號波形的頻譜，將其分別表示為F、H；設聲發(fā)射傳播介質(zhì)中聲阻抗比的數(shù)組為an(x)，表示猜測的模型參數(shù)；根據(jù)猜測參數(shù)an(x)及輸入F正演得到的模型B端的理論波形的頻譜值Y[an(x)]，則可設定反演參數(shù)an(x)對應的接收信號與實際在B段接收的信號的頻譜值之間差的范數(shù)為目標泛函[15]

(9)

(10)

不難看出，該反演問題可以演化為最優(yōu)化問題，且目標泛函和模型參數(shù)之間為復雜的非線性關系，求該目標泛函的最小二乘解可以反演出模型各層間聲阻抗比值的分布。

根據(jù)上述的反演方法的原理不難發(fā)現(xiàn)，只通過斷鉛點和響應點的聲發(fā)射信號來反演聲阻抗值會存在聲阻抗測量區(qū)域過大，聲發(fā)射信號在傳播過程中發(fā)生過多的反射和透射疊加導致測量誤差大的問題；并且由于用于正演的波幅轉換關系是建立在理想情況下的頻域分析，其獲得的輸出波形的畸變程度遠不及實際情況的大，所以需要對兩輸入、輸出波形之間的波動情況進行分析，用得到的前后兩波形作為新的輸入、輸出波形進行反演計算，以達到減小輸入、輸出波形間畸變程度以及通過兩傳感器采集到的輸入、輸出波形就可以得到任意位置的聲阻抗，而無需設置更多傳感器的目的。

將通過一維波動方程問題的求解得到聲阻抗測量區(qū)域任意層的聲發(fā)射波形，從而在之前的工作的基礎上反演得到任意層的聲阻抗值。設波動沿水平x方向傳播，垂直方向上質(zhì)點位移為w，c為傳播速度，則問題描述的波動方程為[16]

(11)

式中：0≤x≤L,t≥0

初始條件為

w(x,0)=wt(x,0)=0

(12)

邊界條件為

(13)

附加條件為

w(L,t)=h(t),t≥0

(14)

式中，h(t)為接收點探頭信號。

由此，構成了單參數(shù)識別問題的數(shù)學模型，可以通過聲發(fā)射儀器測量輸入端、輸出端之間的區(qū)域的波速，代入及采用有限差分法來求解波動方程，得到任意離散后每一層的波形，繼而反演計算出輸入端、輸出端之間的區(qū)域內(nèi)的不同層間的聲阻抗比值的分布。

1.3 正反演數(shù)值模擬實例

為了檢測上述方法、模型是否可靠，對其進行數(shù)值模擬，研究突發(fā)型聲發(fā)射在非均勻損傷區(qū)域AB中的傳播。設AB寬D=1 m，泊松比0.269，密度7 890 kg/m3，彈性模量210 GPa，在探頭A處給定一個簡化突發(fā)型聲發(fā)射輸入，圖3即該突發(fā)型聲發(fā)射信號的包絡波形。

圖3 聲發(fā)射信號模擬波形

將AB中間待測區(qū)域視為1層，則加上左右兩側總共有三層，對這三層如圖4所示設置對應的聲阻抗值，并且以該值作為真實值進行正演，得到入射波和透射波的振幅頻譜圖以及透射波的時域圖,如圖5所示。

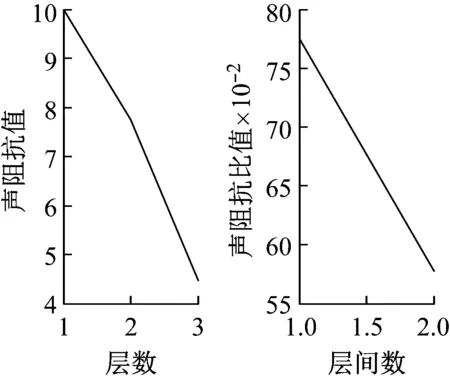
圖4 各層聲阻抗值及其間比值

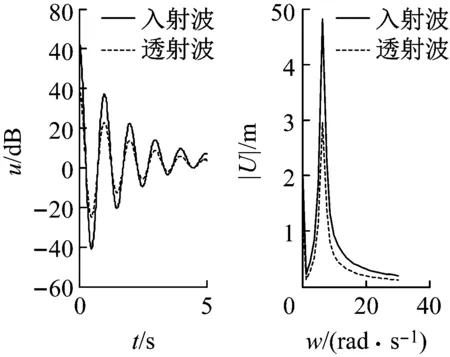
圖5 入射波、透射波時域及頻域圖

Fig.5 Time and frequency presentation of the incident wave and transmission wave

使用正演模型實例獲得的B端理論波形作為已知的輸出波形，則通過已知輸入、輸出波形對原聲阻抗比值進行反演計算。假設此時不知道反演區(qū)域到底是多少層，那么假設反演區(qū)域分為10層，取反演精度ε=10-12，得到反演結果如圖6所示。

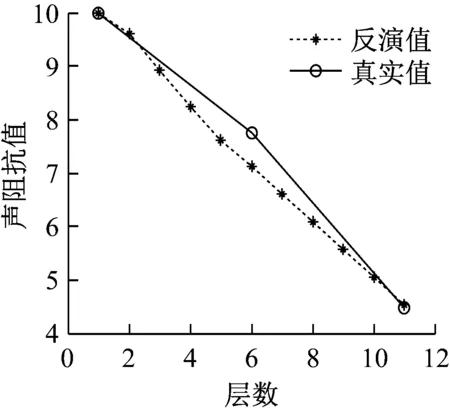
圖6 聲阻抗模型反演

從圖6可知，聲阻抗值的反演值與實際值分布規(guī)律、變化趨勢一致；且聲阻抗值的反演結果與真實值最大相對誤差為9.5%，曲線擬合相關系數(shù)為0.999 134 648，說明數(shù)值分析的模擬結果與聲阻抗比值實際值基本吻合，基本達到實驗目的，可以進行實驗。

2 估算服役并卸載后金屬的聲阻抗實驗

2.1 實驗方案設計

實驗系統(tǒng)由拉伸試驗機和美國物理聲學公司生產(chǎn)的PCI-2聲發(fā)射測試分析系統(tǒng)組成。實驗用拉伸試樣是工程采用常用材料Q235制成的拉伸件，尺寸為210 mm×30 mm×1 mm，Q235鋼在無損情況下的聲阻抗值約為4.53×106g/cm2·s。制備出受最大拉力分別為0、4 kN、8 kN、12 kN、14 kN的待測件，即得到不同拉伸損傷的金屬材料試件，分別對承受過0、4 kN、8 kN、12 kN、14 kN拉伸力損傷的試件進行斷鉛試驗。試驗采用伸長量約2.5 mm的直徑為0.5 mm的HB鉛芯，將其與待測試件之間夾約30°角并且均勻壓斷鉛芯，每組試件進行三次試驗，記錄其平均值。在斷鉛點進行斷鉛并采集聲發(fā)射輸入信號，在響應點采集聲發(fā)射響應信號，斷鉛點及響應點中間即為檢測區(qū)域，將檢測區(qū)域兩側視為未受損區(qū)域，即聲阻抗值與未受損時的試件的初始值相等,如圖7所示。假設測量區(qū)域的聲阻抗層數(shù)分為10層，則從斷鉛點到第一層之間算起，各層間總共有10個聲阻抗比值，聲阻抗比值為[a1a2a3a4a5a6a7a8a9a10]。

圖7 試件上斷鉛點、響應點及分層示意圖

Fig.7 The points for the pencil lead breaking and measuring in the specimen

2.2 實驗結果分析

根據(jù)斷鉛聲發(fā)射信號的聲阻抗估算方法，得到聲阻抗前后比值-層數(shù)結果如圖8所示。

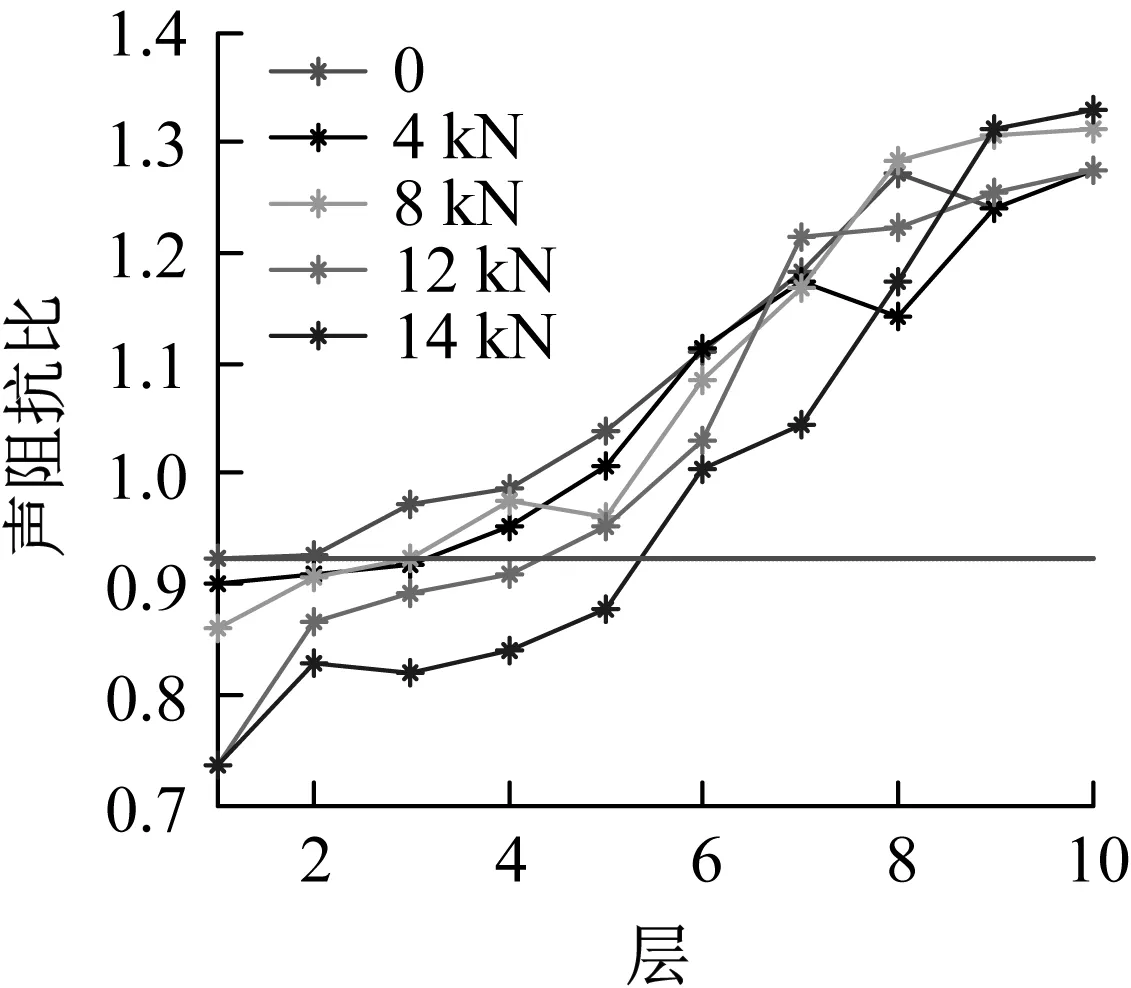
圖8 聲阻抗比-層數(shù)相關圖

反演得到的聲阻抗比值在1附近范圍波動，可以看到，以試件的0聲阻抗比值的最小值為臨界點，隨著損傷程度的增加，處于臨界位置下的值增加；從整體看，隨著聲阻抗層從左向右(見圖7)，聲阻抗的比值相對上升，這主要是因為在聲發(fā)射信號從斷鉛點開始傳播的過程中，一開始隨著層數(shù)的增加，材料損傷增大，因為裂隙和缺陷不斷增多，而空氣的聲阻抗值比金屬小得多的原因，聲阻抗值呈減小狀態(tài)，故聲阻抗比值較低且小于1；隨著聲阻抗層更靠右(見圖7)，這時候由接近損傷位置到遠離損傷位置，聲阻抗相對上升，故聲阻抗值相對較高并大于1。

由于實際試驗中金屬材料試件并不是無限長，聲發(fā)射信號傳播過程中發(fā)生不斷散射與反射，導致根據(jù)反演得到的聲阻抗比值計算的聲阻抗值超出初始設定值，為了更好地進行分析，將Q235鋼在無損情況下的聲阻抗值(4.53×106g/(cm2·s)設為最大值，得到各不同狀態(tài)下試件的聲阻抗成像,如圖9所示。

圖9 反演得到的聲阻抗成像圖

從圖9可知，隨著損傷程度的增加，試件的聲阻抗明顯降低;隨著試件損傷程度的增加，損傷范圍明顯增大，并且損傷區(qū)域集中在試件中段，與實際拉伸情況相符合，從而可以在一定程度上實現(xiàn)損傷定位。

3 結 論

通過反演和實驗可知，聲阻抗是隨著損傷程度的增加而減小。而在損傷較小時，通過斷鉛試驗聲發(fā)射信號估算聲阻抗靈敏性更高，即采用斷鉛試驗聲發(fā)射信號能夠分辨出更加微小的損傷，說明在金屬材料的微損傷階段，運用斷鉛激勵能夠?qū)崿F(xiàn)產(chǎn)生更有效的輸出響應信號，為材料微損傷的無損檢測的研究提供了實驗參考。

(1) 通過聲發(fā)射相關參數(shù)反演聲阻抗比值求得聲阻抗值，無需再對材料密度進行測量，估算測量過程相對簡單、方便，還可進行實時監(jiān)控。 靜態(tài)情況下計算聲阻抗值的方法可滿足各種測量環(huán)境，而且打破了聲發(fā)射應用的局限性，為未來聲發(fā)射更廣闊的應用奠定了基礎。

(2) 采用聲發(fā)射測量聲阻抗，對比超聲的檢測方法，聲發(fā)射由于自身的優(yōu)越性可以對不規(guī)則的外形的試件進行激勵檢測，為金屬材料聲阻抗損傷反演的進一步工程應用提供理論和實驗依據(jù)。采用本研究的反演方法，能夠簡單直觀地反應材料的整個損傷程度，并且能夠在一定程度上對損傷進行定位。

(3) 采用斷鉛聲發(fā)射激勵有空隙、微裂紋等微損傷的試件，估算的聲阻抗可表征其損傷，可為設備故障預測與健康管理提供參考。