基于偏移量控制的MPC算法在預扭葉片振動控制中的應用

劉廷瑞, 常 林

(山東科技大學 機械電子工程學院過控系，山東 青島 266590)

風力機葉片的氣彈不穩定性是葉片斷裂失效的重要原因，其中揮舞/擺振運動造成的失效是主要表現[1]。近期發生在世界各地的風力機葉片斷裂失效也驗證了這一問題[2]，因此探尋葉片揮舞/擺振振動控制方法具有積極的意義。近年來諸多學者針對不同的葉片結構模型發展了諸多風力機葉片顫振抑制方法，其中2D典型截面模型由于高效方便，而又能集中分析典型的發散不穩定振動問題而被廣泛采用。

典型截面模型早期由Chaviaropoulos提出并進行了氣彈分析[3]。該模型建立在2D翼型截面基礎上，通常通過分析揮舞/擺振、揮舞/扭轉耦合位移來研究不同的氣彈現象。文獻[4]對典型截面的揮舞/擺振/扭轉耦合運動進行了建模，并通過線性二次型控制及模糊控制策略研究了發散不穩定控制問題；文獻[5]研究了大位移變形的經典顫振不穩定現象，并通過時域響應和頻率結構分析研究了葉尖揮舞/擺振/扭轉位移；而課題組成員也曾在前期工作中對2D葉片的氣彈不穩定進行了智能PID控制策略的研究[1]。然而上述方案均未涉及到2D翼型截面的完整的結構阻尼的描述，其阻尼行為僅僅限于弦向和法向的阻尼(不完全阻尼)行為的集成，未考慮葉片彈性扭轉或葉片預扭對阻尼變化的影響。

文獻[6]考慮了彈性扭轉及葉片預扭對復合材料振動行為的影響，但限于3D直升機葉片，且忽略了其中的結構阻尼。對于3D葉片體而言，復合材料葉片結構阻尼的計算是一個比較復雜的問題，至今尚無統一的計算方法。項目組成員在前期工作中，考慮彈性扭轉及葉片預扭，計算了3D葉片體結構阻尼，發現結構阻尼的影響是至關重要的[7]。對于2D翼型截面而言，揮舞/擺振線位移方程中的結構阻尼的估算同樣尚無定論，但文獻[8]曾基于角位移方程估算了結構阻尼系數。本文在前期工作基礎上，引入了縮減時間概念，進行了2D翼型線位移到角位移的變化，并結合文獻[8]的阻尼計算方法，實現了基于完全結構阻尼的2D翼型角位移的結構建模。另外，線性二次型控制(LQR)經常用來對旋轉體的發散不穩定性進行控制[9], 但由于其在初始振動幅度的抑制方面具有先天性的缺陷，在實際應用中，需加大控制量方能達到較為理想的效果。本文基于發散振動的不穩定性，采用了一種基于偏移量控制的模型預測控制(MPC)算法[10-12]，并在LQR控制的加權值基礎上創新性地構建了一種罰權值，來構建MPC算法的控制性能指標，不僅大幅度減小了控制量，而且使發散運動達到了急速收斂的目的。

1 理論建模

1.1 結構模型及運動方程

考慮大長徑比2D翼型典型截面，截面位置距離葉根r處，如圖1所示。y，z方向分別代表擺振和揮舞方向的運動(位移)，且α為攻角；U為風速；c為弦長(弦向方向為t，法向方向為n)；V0為相對風速；λ為速比系數；葉片展長L=15 m；轉速為Ω=λU/L=2U/L。θ=(r/L)×θ0為預扭角。其它結構參數包括：ωt、ωn分別為弦向和法向頻率；ξt、ξn分別為弦向和法向阻尼比；ρb為截面元密度。

圖1 2D翼型典型截面位移坐標及參數

考察文獻[1]的截面線位移模型，剔除其中的不完全阻尼行為，并令縮減時間τ=tV0/c，截面揮舞角βz=zc/r，截面擺振角βy=yc/r，則描述揮舞角/擺振角的運動方程可以表達為

(1)

式中，Cy、Cz分別為擺振和揮舞方向的氣動系數。

本文利用葉片預扭角θ來增加扭轉剛度，并為系統提供完全阻尼行為。根據文獻[8]之推導，結構阻尼系數可以描述為

(2)

式中，T為預扭效應系數，Cs0為縮減的阻尼矩陣，分別寫作

(3)

則完全結構阻尼系數矩陣可以表達為ΩCs。類似地，有相應的結構剛度系數

(4)

則完全剛度系數矩陣可以表達為

(5)

在此基礎上可以獲得新的運動方程如下

(6)

式中：CL、CD分別為氣動升力系數和氣動阻力系數。

1.2 模型參數計算

對于不同位置r處的截面，有著不同的弦長c和元密度ρb。文獻[13]基于NA63215翼型，在葉素-動量理論的基礎上，利用Wilson迭代法優化設計了不同的位置r處的弦長c。本文在此基礎上，繼續優化了元密度ρb，并將相關各個參數擬合為“六級正弦和(Sin 6)”曲線，表達為

(7)

式中：w=r/L；系數ai,bi,ci參見表1所示。

翼型氣動系數CL、CD的準確性和完備性對葉片設計意義十分重大。本設計在文獻[13]基礎上，利用Xfoil軟件及AirfoilPrep軟件，獲得了攻角α在-90°～90°范圍內的升、阻氣動系數CL、CD，同樣將其擬合為Sin 6曲線，在Sin 6曲線中,w=α；相關系數ai、bi、ci亦參見表1。

表1 Sin 6模型中不同參數的系數

(8)

式中：Ac、Cc均為4×4系數矩陣，Bc為4×1系數矩陣。

2 MPC控制算法

根據處理對象的不同，MPC有諸多不同的算法，包括標準優化MPC(隱式MPC)、終端權值MPC、顯式MPC，以及適用于非線性系統的自適應MPC和多重MPC[14]。本文在標準優化MPC的基礎上，采用文獻[12]的狀態空間表達的MPC算法，并結合LQR控制中的加權矩陣系數，構建了基于罰權值和設定點跟蹤的MPC偏移量控制算法，對葉片的發散行為進行了控制。

首先，對系統方程(8)進行離散化，得到：

(9)

式中：ηx、ηy為預測模型與實際模型之間的偏移量。

將上述方程寫為增量形式

(10)

式中:I為單位矩陣。然后進一步定義新的狀態變量X(k)=[Δx(k)Tym(k)T]T，將式(10)重寫為

(11)

其中，

根據系統方程(11)，預測未來第k+j(j=1,2,…,p)時刻的運動軌跡為

(12)

式中：p、pc分別為預測水平和控制水平。

其次，為進行控制性能的對比研究，本文同時設計了LQR控制器，并假設LQR控制器的加權值矩陣分別為Q、R，且Q=10I4×4，Q(1,1)=100,Q(2,2)=99,Q(3,3)=98、R=0.01。在偏移量控制的MPC中，為充分利用LQR控制的優點而加速收斂，取相應的偏差域和控制域罰權值矩陣分別定義為

(13)

則相應的控制性能指標可以描述為

Jmin=ΔYTYwΔY+ΔuTuwΔu

(14)

同時在偏移量的控制中需給定輸出信號的目標值為

Yr=10reI1×4

(15)

式中：re為目標調節的性能參數。

3 振動控制及控制性能分析

取基本結構參數和運動參數：ωn=4 rad/m,ωt=8 rad/m,ξn=0.02,ξt=0.04，U=10 m/s。考慮危險截面一般位于1/4L～1/3L的展長范圍，特取截面半徑r=5 m。控制水平pc和預測水平p滿足固定關系式pc=p-1。為展示結構阻尼效應，本文在不同初始預扭角θ0情況下，分析揮舞運動z(r,t) 以及擺振運動y(r,t)的發散不穩定位移并展示MPC控制結果。由于系統(11)求解結果為揮舞角/擺振角的角位移，特通過第一節所述變換，將求解結果轉化為揮舞/擺振線位移進行顯示。

3.1 振動控制

令初始預扭角θ0=5°，預測水平p=15，目標調節的性能參數re=0.1。圖2分別展示了未控制時的發散不穩定位移(a)、LQR控制下的位移及相應的控制信號(b)，以及MPC控制結果及相應的控制信號波動(c)。可以看出：從控制趨勢看，LQR控制雖然能使位移收斂，但其擺振運動的穩態值卻大于截面半徑r，故在工程實際上看，仍然處于發散不穩定狀態。而對于揮舞/擺振位移，MPC控制無論從振動幅度、穩態時間、穩態值都處于極好的調節狀態，且控制信號u非常平穩，幅度也較小，體現了良好的控制性能，也展示了MPC控制相對于LQR控制非常明顯的優越性。同時可以看出MPC控制對擺振運動控制良好，其控制幅度與目標調節的性能參數re=0.1幾乎處于同一水平，體現了控制算法實施的精確性；而MPC控制對揮舞運動的控制效果更佳，控制穩態值相對更小。

另外需要強調的是：圖(b)展示的LQR相應的控制信號的幅度達到了650 m (此處m為當量單位)，這就意味著更大的控制代價和能量消耗，是不合理的。而無論從被控對象還是控制器本身的響應看，圖(c)展示的MPC控制的穩態時間都是很小的，反映了控制調節的快速性。

(a) 發散不穩定位移 (b) LQR控制位移及相應的控制信號

(c) MPC控制結果及相應的控制信號

圖2 初始預扭角θ0=5°條件下的未控制的發散不穩定位移、LQR控制下的位移，以及MPC控制結果及相應的控制信號

Fig.2 Uncontrolled divergent displacements, cases controlled by LQR, and results controlled by MPC with corresponding manipulated signal based onθ0=5°, respectively

為檢驗控制算法的普適性和結構阻尼的影響，圖3展示了初始預扭角θ0=60°，預測水平p=15，目標調節的性能參數re=0.1的情況下的發散不穩定未控制位移(a) 、LQR控制下的位移(b)，及MPC控制結果(c)。與圖2相比可以看出：MPC控制揮舞位移在一次波動后，仍然能急速穩定，穩定幅度在同一數量級水平；MPC控制擺振運動與圖2相比變化不大，穩定幅度也處于同一數量級水平，控制信號相比較幅度稍大，但仍然在同一數量級水平，體現了良好的控制性能。而MPC控制相對于LQR控制而言，仍然具有絕對的優越性。

需要強調的是：與圖2相比，圖3中MPC控制器響應幾乎沒有超調量，可有效避免控制器本身過載區的控制沖擊。另外與圖2相比，圖3中的被控揮舞/擺振位移(無論是MPC控制還是LQR控制)和MPC控制信號本身的穩態時間略有減小，以及圖2～圖3中未控制的發散不穩定位移的區別，也正好展示了不同預扭角度的影響，也即結構阻尼效應的影響，從中也體現了葉片結構模型中納入完全結構阻尼的意義所在。

鑒于揮舞斷裂失效在葉片失效中占有更大的比重，圖4則特別展示了初始預扭角θ0在(0°～90°)范圍內，每間隔10°，相應不同的結構阻尼下的MPC對揮舞運動的控制結果。可以看出：整個揮舞運動控制均能限制在(-0.005～0.045)的范圍，體現了MPC控制的魯棒性。同時也看出對不同的結構阻尼狀態下的控制效果有明顯差異，也進一步論證了本文進行完全結構阻尼計算的必要性。

(a) 發散不穩定位移

(b) LQR控制位移

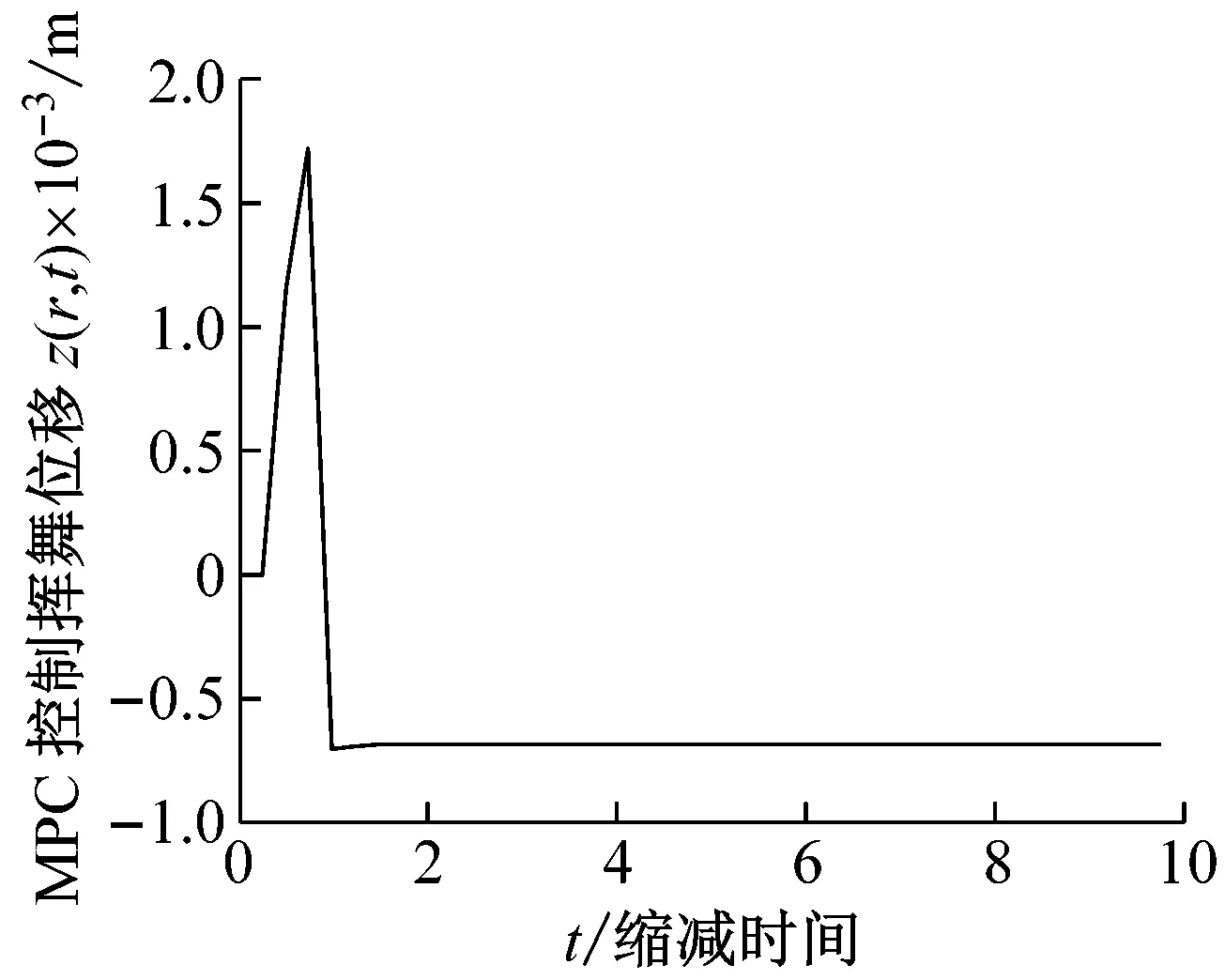
(c) MPC控制結果及相應的控制信號

圖3 初始預扭角θ0=60°條件下的的未控制的發散不穩定位移、LQR控制下的位移，及MPC控制結果及相應控制信號

Fig.3 Uncontrolled divergent displacements, cases controlled by LQR, and results controlled by MPC with corresponding manipulated signal based onθ0=60°, respectively

圖4 初始預扭角θ0在(0°～90°)范圍內，每間隔10°，相應不同的結構阻尼下的MPC控制結果

Fig.4 Results controlled by MPC based onθ0within the range of (0°～90°) at interval of 10°, respectively

3.2 控制性能分析

預測水平p對于MPC控制效果具有顯著的影響。在經驗設計中一般要求p大于狀態變量的個數，且不能過分大。令初始預扭角θ0=60°，目標調節的性能參數re=0.1，圖5展示了不同預測水平下的揮舞位移(a)、擺振位移(b)、控制信號(c)。可以看出：太小的預測水平p=5控制下，無論揮舞/擺振位移還是控制信號，都處于逐漸發散狀態，即使經過較長的時間后能夠收斂穩定，都因穩態時間太長而屬于欠佳的調節性能；而太大的預測水平p=16控制下，無論揮舞/擺振位移還是控制信號，都急速發散。故在本設計中，取預測水平系數10≤p≤15，可以取得良好的控制效果。

另外，仿真結果表明：不同目標調節的性能參數re下控制效果不同。令初始預扭角θ0=60°，預測水平p=15，圖6展示了不同目標調節的性能參數re下的揮舞位移(a)、擺振位移(b)、控制信號(c)。可以看出：無論對于揮舞/擺振的位移信號還是相應的控制信號，當目標調節的性能參數re越小，位移信號和控制信號的幅度值相應越小，表明了re較小時控制性能更優越。但從控制器硬件(比如用于作為風電控制器的PLC控制器)對被控信號的捕捉、對控制信號的操作角度講，太小的信號無法被控制器所識別，會帶來控制隱患，甚至完全失去效用。而太大的目標調節的性能參數re，會降低偏移量的控制效果，使輸出信號和控制信號均太大，達不到控制要求。如圖6中re=1時，擺振位移的控制，雖然控制趨勢良好，但擺振位移的幅度達到了10 m，遠遠超過了截面半徑r=5 m，工程實際上也是處于發散不穩定狀態，未達到控制要求；而相應的控制信號的幅度也達到了28 m (此處m同為當量單位)，這就需要更大的控制代價和能量消耗，也是不合理的。故在本設計中，取目標調節的性能參數-2≤re≤0，可以獲得良好的控制效果。

(a) 不同預測水平下的揮舞位移

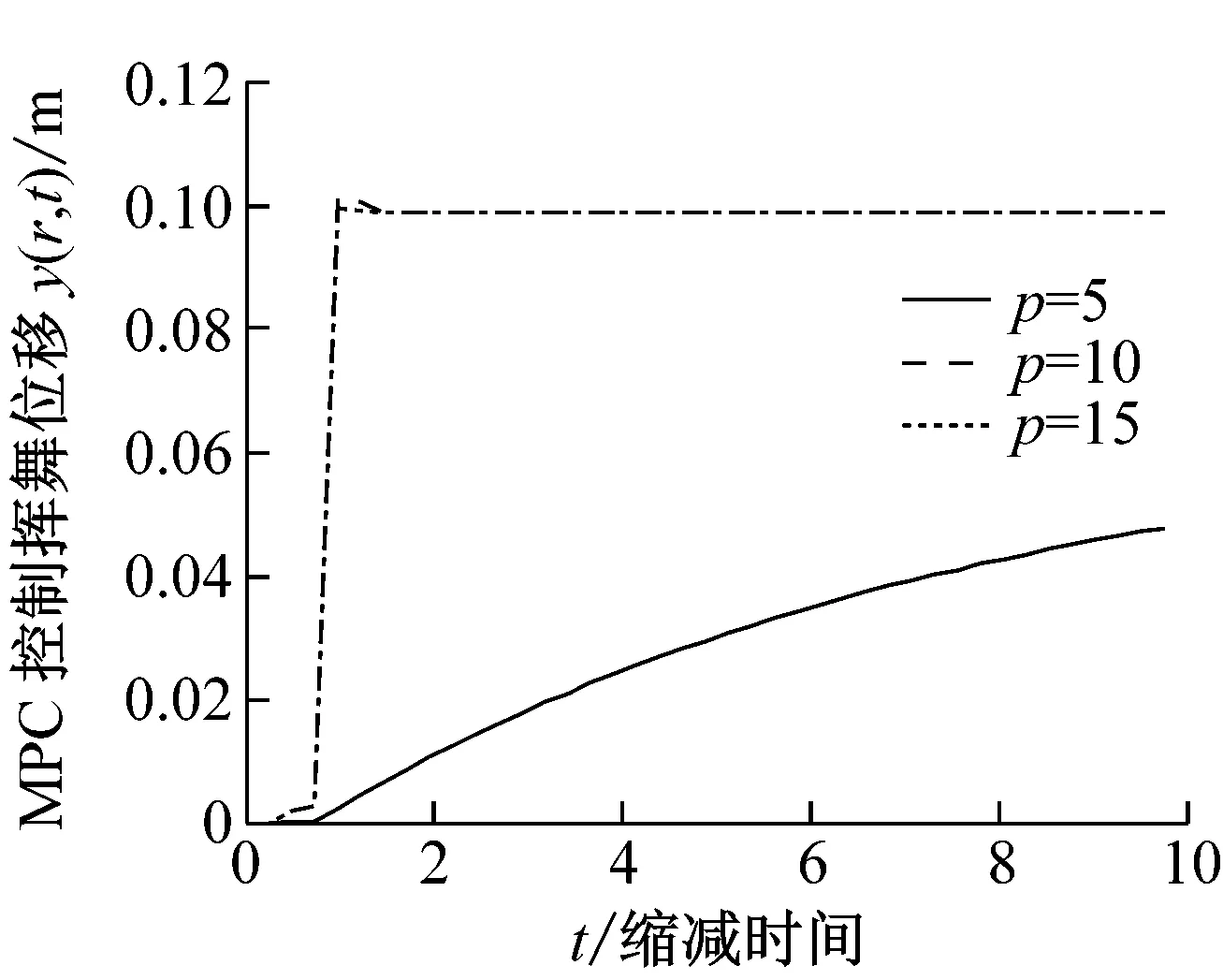
(b) 不同預測水平下的擺振位移

(c) 不同預測水平下的控制信號

圖5 不同預測水平下的揮舞/擺振位移及控制信號

Fig.5 Flap/Lag displacements and manipulated signals under different parameters of prediction horizon

與圖5對比可發現：圖5中不同的預測水平p可以極大地影響穩態時間，而圖6中不同的目標調節參數re則幾乎對穩態時間沒有選擇性影響，并能極大地保證穩態時間的優越性，而更側重影響振動幅度，故在實際應用中，p與re的選擇具有折中與協調考慮的必要性。

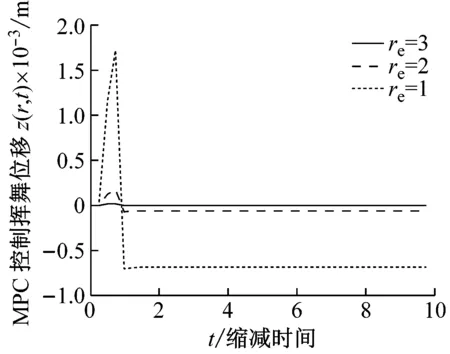
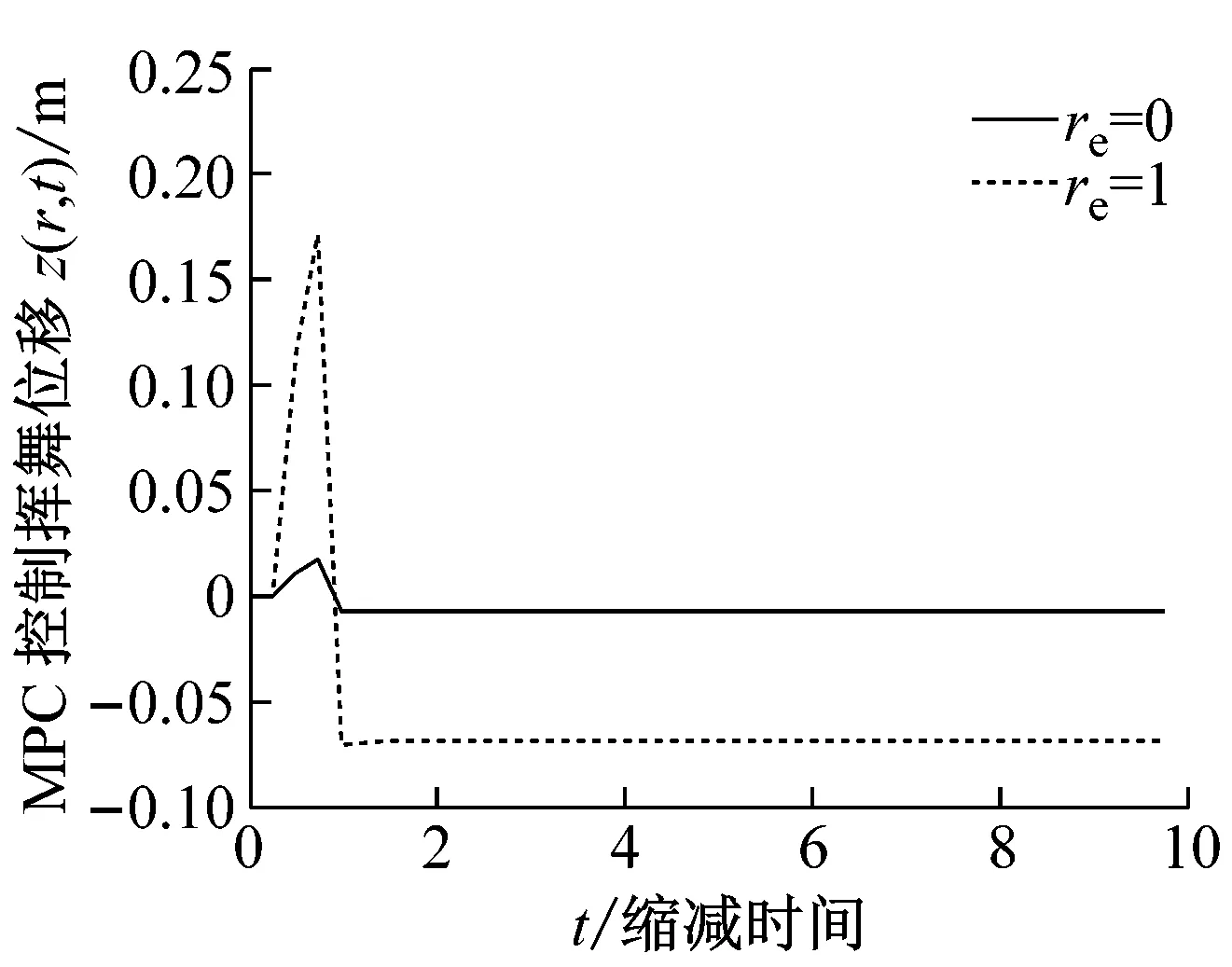
(a) 不同目標調節的性能參數下的揮舞位移

(b) 不同目標調節的性能參數下的擺振位移

(c) 不同目標調節的性能參數下控制信號

圖6 不同目標調節的性能參數下的揮舞/擺振位移及控制信號

Fig.6 Flap/Lag displacements and manipulated signals under different performance parameters of target regulation

另外，從實際應用方面，以目標值為控制的前提：是能夠有效地反饋測量值。項目組成員在前期工作中，在薄壁葉片中嵌入ASF壓電材料[15]，能有效地將所測截面的揮舞/擺振位移，反饋成電信號，該電信號與位移有近似的估計表達式，從而實現了測量值的反饋。而在工程實踐中，可以利用偏差信號來驅動外部變槳運動。傳統的外部變槳一般可以等效為“轉速偏差”的二階PID控制系統，而高精度的PID控制本身也是復雜的。本文的MPC“位移偏差”控制可以取代“轉速偏差”PID控制來描述變槳運動的規律，這也是本設計后續工作展望。

4 結 論

(1) 發散不穩定分析是建立在2D典型截面模型基礎上，并考慮了完全結構阻尼效應，氣動力是基于數據擬合的Sin 6氣動力模型。擬合氣動模型的本身可以消去由于氣動變量本身帶來的氣動方程，從而減少系統方程的個數，為后續MPC控制降低了計算工作量。

(2) 基于MPC控制，通過位移響應分析了控制效果，不僅論證了完全結構阻尼計算的必要性，也通過對比論證了MPC算法的魯棒性。本設計MPC控制優越性的機理在于：基于偏移量控制可以利用MPC算法的狀態空間模型，從而極大地減小計算工作量；基于罰權值的構建可以充分利用LQR控制的優點并加速收斂過程；基于目標調節的性能參數re的研究可以確定合理的被控信號的幅度及控制信號的規模，并保證穩態時間的優越性。

(3) 鑒于預測水平p的重要性，本設計利用位移響應和控制信號響應趨勢和穩態時間的對比，探討并確定了預測水平p的合理取值范圍，同時論證了與目標調節參數re折中選擇的必要性。為同類MPC控制的預測水平的確定提供了可行性方案。