聲彈效應測量螺栓軸向應力的有限元計算分析

孫朝明， 王增勇， 李建文， 孫凱華

(中國工程物理研究院 機械制造工藝研究所，四川 綿陽 621900)

螺栓被廣泛應用于多種機械部件間的緊固連接，而螺栓的拉緊狀態(tài)很大程度上決定了連接件的使用性能。為使緊固件達到預定的使用壽命，需借助于擰緊螺母的方式將螺栓調(diào)整到一定的預拉緊狀態(tài)；此時，預緊力的合理控制則至關(guān)重要：過小的預緊力會導致緊固件間出現(xiàn)松動、結(jié)構(gòu)滑移而影響部件使用，過大的預緊力則會增加螺栓的載荷并易產(chǎn)生斷裂失效。有研究表明，航天結(jié)構(gòu)所用緊固件有82.5%的失效與螺栓緊固狀態(tài)控制不當有關(guān)[1]。因此，螺栓預緊力大小的準確測量，在工程上具有重要意義且需求明顯：可準確獲知螺栓的工作狀態(tài)并做出相應調(diào)整，可監(jiān)測出螺栓經(jīng)一定時間后的狀態(tài)變化情況。目前來看，對螺栓擰緊狀態(tài)檢驗的操作方法還相對粗略，有待改進。

聲彈效應[2-4](超聲聲速與工件的彈性應變存在關(guān)聯(lián))已應用于螺栓軸向應力的測量，而如何提高測量結(jié)果的可靠性與精度則是需要分析解決的關(guān)鍵問題。Heyman[5]最早構(gòu)建了螺栓軸向應力的超聲測量裝置，隨后出現(xiàn)了不少類似的超聲測量設(shè)備。與其它螺栓應力測量手段相比，超聲技術(shù)具有突出優(yōu)點，對工件無損傷、對人體無害、測量便捷、成本低。雖然聲彈效應的發(fā)現(xiàn)時間比較早，在多個行業(yè)中應用潛力較大，不過要在工程上成功應用并不容易。實際上，為評價超聲技術(shù)測量軸向應力的可靠性，需要研究分析螺栓軸向應力變化如何導致超聲信號變化；為提高測量結(jié)果的精度，需要準確認識各因素對超聲波信號特征的影響，有效增強超聲波信號識別特征，構(gòu)建精確的測量模型。目前來看，螺栓軸向應力的超聲測量研究工作傾向于試驗分析[6-12]，數(shù)值模擬分析[13-14]的應用很少；主要原因在于聲彈效應表現(xiàn)出較為復雜的非線性特征，而目前很多數(shù)值模擬分析軟件(如Abaqus、Ansys、CIVA)中卻沒有構(gòu)建相應的模型去描述這一非線性。借助于有限元方法，Sanderson等對使用激光超聲測量鋼板殘余應力的方法進行了分析，Watson等對三點彎曲試驗情況下超聲與載荷間的關(guān)系進行了計算分析；但SANDERSON的分析是借助于Abaqus來進行的，而在Abaqus的材料庫中并沒有合適的材料模型去描述聲彈效應；Watson利用Comsol軟件進行了聲彈效應的分析，在分析時卻借助于人為增加聲彈系數(shù)的方式進行求解分析，而事實上材料的基本屬性參數(shù)并不包含聲彈系數(shù)，這就造成模擬分析結(jié)果與試驗結(jié)果存在偏離。對于工程應用而言，應更多關(guān)注于超聲時域信號的準確獲取，但在Sanderson和Watson的研究結(jié)果中卻并沒有看到。

為促進聲彈效應在定量評價螺栓擰緊狀態(tài)中的有效應用，結(jié)合實際檢測需求，作者建立了超聲法測量螺栓軸向應力的二維軸對稱有限元模型，分析了螺栓在軸向載荷作用下的應力狀態(tài)，分析了超聲波在螺栓內(nèi)的傳播特性，分析了由于軸向應力、螺栓夾緊長度、螺栓材料而引起的超聲傳播的時差情況。通過分析，闡明了螺栓內(nèi)部應力狀態(tài)對于超聲傳播聲時變化的疊加影響，闡述了由于夾緊長度不同而引起的聲彈效應的差異。將有限元計算結(jié)果與解析模型計算結(jié)果、試驗分析結(jié)果進行了對照，驗證了有限元計算模型的準確性。基于此模型，能夠針對特定檢測配置給出相應的超聲時域信號，從而可為檢測方法分析、專用儀器研發(fā)提供有價值的參考。

1 聲彈效應的理論基礎(chǔ)

1.1 應力方程

對于彈性固體，在受力后將產(chǎn)生變形。分別用(a1,a2,a3)、(x1,x2,x3)表示彈性固體形變前后的點位置坐標，變形前后的單元體積可用下式描述[15]

dx1dx2dx3=|J|da1da2da3

(1)

式中:J為雅可比矩陣，矩陣中的元素可記為

(2)

式中:i、l為矩陣的行列序號(1～3)。

一般情況下，固體形變前后弧元的長度會有所改變。考慮用3×3的應變矩陣η描述形變大小

(3)

式中:JT為J的轉(zhuǎn)置矩陣；I為單位矩陣。

通過拉格朗日方程，可推導得到應力方程

(4)

式中:ρ0為固體材料密度；Tik為應力；i、k為矩陣的行列序號(1～3)。

式(4)中的應力與單位體積中的勢能存在關(guān)系

(5)

1.2 彈性勢能

理想情況下，可認為固體受力變形后各種力所做的功都轉(zhuǎn)化為彈性能，彈性能只與應變有關(guān)。

對于各向同性的彈性體，彈性勢能只是三個特定數(shù)值的函數(shù)。這三個數(shù)值分別用I1、I2、I3表示，稱為旋轉(zhuǎn)不變量。旋轉(zhuǎn)不變量與應變參數(shù)間存在關(guān)系如下

I1=η11+η22+η33

(6)

(7)

(8)

式(6)～式(8)表明，I1、I2、I3分別為應變量的一次、二次、三次函數(shù)。

將彈性勢能展開為應變的二次型函數(shù)，結(jié)果為

(9)

式中:λ、μ為二階彈性常數(shù)或稱為拉梅常數(shù)。

引入三階彈性常數(shù)l、m、n(默納漢常數(shù))，用應變的三次型函數(shù)描述的彈性勢能為

(10)

結(jié)合式(9)、(10)，總的彈性勢能可寫作

(11)

1.3 軸向拉應力作用下縱波聲速的變化

在軸向拉應力的作用下，應力矩陣中只有T11取值為-T，其余元素均為0。

由虎克定律易知應力作用下的位移分量，考慮泊松效應，將位移量計算結(jié)果代入式(4)描述的應力方程，可得到軸向應力作用下，縱波聲速變化規(guī)律如下

(12)

式中:v0、v分別為應力加載前后的縱波速度。

對螺栓工件，軸向應力可用下式描述

(13)

式中:E為彈性模量；L0、ΔL分別為螺栓的初始長度、螺栓在軸向應力下的伸長量。

對式(12)進行一階近似，將非線性關(guān)系轉(zhuǎn)換為線性關(guān)系,可得：

v=v0(1+AlT)

(14)

式中:Al為聲彈系數(shù)，它可用下式描述

(15)

螺栓在軸向拉伸前，超聲在其中傳播所需時間為

(16)

螺栓在軸向拉伸后，超聲傳播時間會增加。通過偏微分計算并進行一定近似，可知所增加的時間為：

(17)

由式(17)可知，因聲彈效應而導致超聲聲時變化量與三方面的因素相關(guān)：未受應力時超聲在工件內(nèi)的傳播時間、材料特性參數(shù)(彈性模量和聲彈系數(shù))、軸向拉應力。不過，需要注意的是，上面討論假定螺栓受到均勻的軸向拉伸載荷，式(16)中的L0代表均勻拉伸載荷作用下的螺栓長度。

2 有限元計算模型

2.1 幾何模型

圖1所示為有限元計算時的二維模型，沿y軸旋轉(zhuǎn)對稱。與真實螺栓相比，計算模型進行了少許簡化，省去了螺紋部分的具體特征，將螺母與螺栓聯(lián)接部分簡化為面接觸；在面接觸部位施加沿y軸向下的拉伸載荷，在螺栓頭部的下表面施加固定約束，從而在螺栓中產(chǎn)生軸向應力。

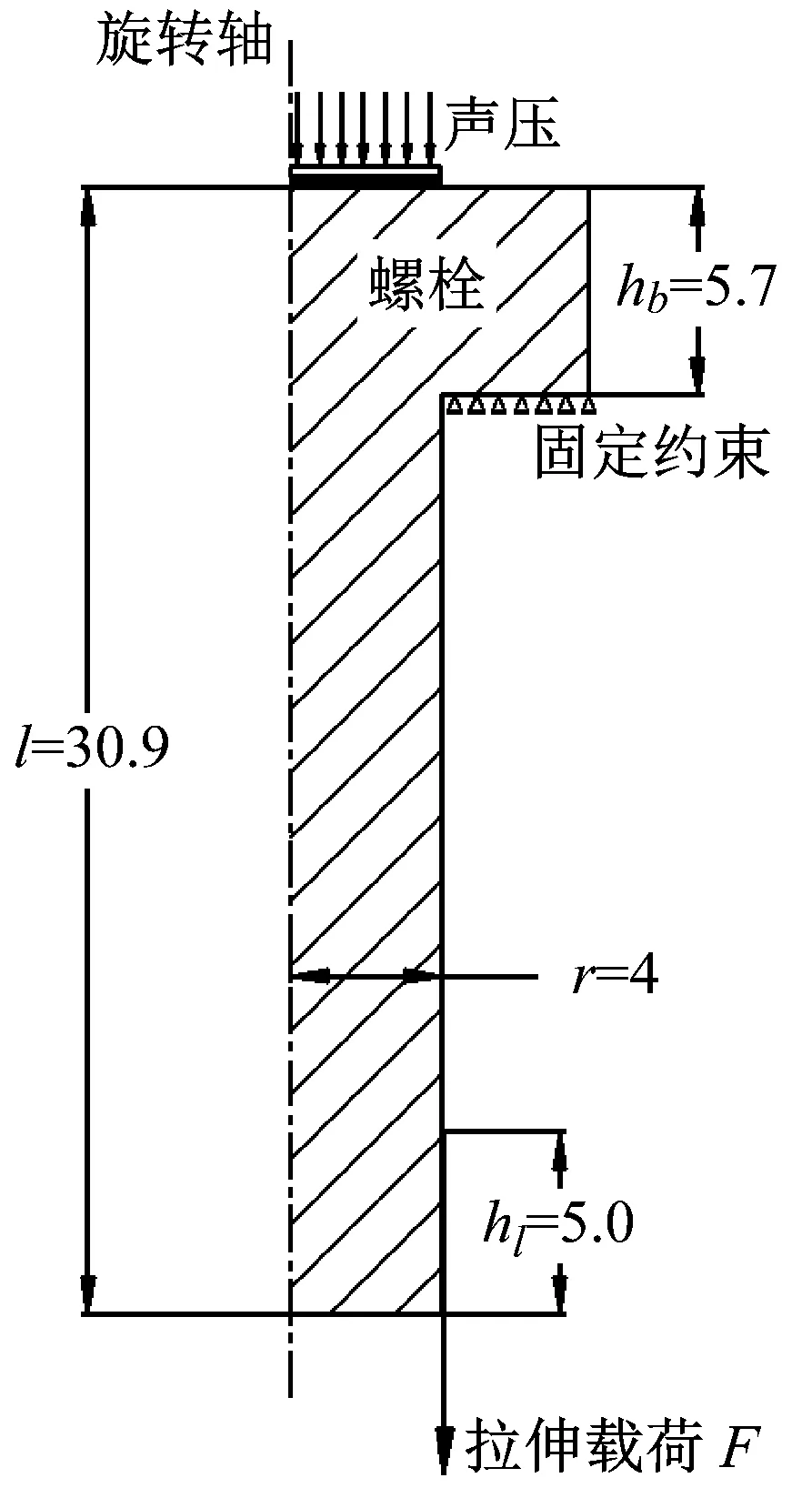
圖1 二維軸對稱有限元模型

模型中的螺栓直徑為8 mm，總長為30.9 mm，頭部高度為5.7 mm。超聲檢測探頭放置在螺栓頭上表面的中心部位，超聲探頭的直徑為8 mm。

2.2 超彈性材料

從式(11)可知,分析聲彈效應時需要考慮三階彈性常數(shù)，這就要求在有限元計算時需包含超聲的非線性特征。本文利用Comsol軟件(版本4.4)進行有限元計算，計算時使用超彈性材料模型。材料模型對應的控制方程保持與式(5)、式(11)一致，從而確保計算結(jié)果的可信度。

有限元模型中引入了默納漢三階彈性常數(shù)(l、m、n)，具體參數(shù)如表1所示。兩種材料分別對應于鋼軌鋼(序號1)、結(jié)構(gòu)鋼(序號2)。

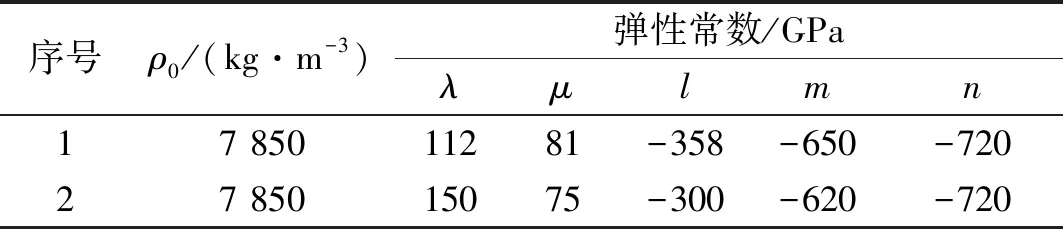
表1 超彈性材料的參數(shù)

2.3 結(jié)構(gòu)場與聲場計算的耦合

在有限元計算時，分為兩個研究步驟：首先，采用結(jié)構(gòu)場進行靜態(tài)加載分析，得到設(shè)定載荷下螺栓所受的應力；然后，將結(jié)構(gòu)場與聲場進行耦合，在包含非線性的情況，計算在一定軸向應力作用下超聲的時變傳播情況。兩個研究步間的相關(guān)變量設(shè)定為壓力和位移場，第一個研究步的解設(shè)定為第二個研究步中求解變量的初始值。

2.4 計算參數(shù)的選擇

超聲激勵信號用下式描述

(18)

式中:P為聲壓；f為超聲頻率；φ為超聲信號的相位控制參數(shù)；B為超聲帶寬控制參數(shù)；t為超聲傳播時間。

計算時，選取超聲頻率f為10 MHz，B為0.03，φ為-π/2，激勵信號在傳播2 μs后達到峰值。

為控制有限元計算精度，在進行網(wǎng)格化時，一般需將網(wǎng)格尺寸設(shè)定為波長的1/10左右。在普通鋼中，10 MHz超聲波對應的縱波波長為0.59 mm。本文分析時將有限元網(wǎng)格尺寸設(shè)定為0.02 mm。

有試驗表明，應力作用下聲速的變化量較小，聲時的測量精度需要達到ns級別。為準確提取超聲信號在傳播時間上的變化，在進行時變分析時設(shè)定時間步長為1 ns(即1×10-9s)。有限元計算的總時長設(shè)定為14 μs。

3 有限元計算結(jié)果分析

3.1 螺栓的應力狀態(tài)

在施加一定軸向載荷后，螺栓內(nèi)部將產(chǎn)生相應的應力。在F為200 MPa時，螺栓的應力狀態(tài)如圖2所示(等值線數(shù)字代表應力值，單位為MPa)。易知工件內(nèi)部應力并是不均勻分布的。事實上，螺栓緊固件在加載后，受力狀態(tài)也是相對復雜的；此種情況下，超聲波信號究竟如何受到軸向應力的影響而產(chǎn)生變化，是值得深入研究的一個問題。

圖2 螺栓內(nèi)部的應力狀態(tài)

從圖2可知，螺栓中間部位的應力較均勻，與施加的200 MPa載荷大小一致；而在螺栓頭部、接觸螺母部位的應力值差異較大。通常，基于聲彈效應測量的螺栓軸向應力是一個確定數(shù)值，此數(shù)值應是螺栓在擰緊狀態(tài)下所受應力的一個綜合評價指標。

3.2 超聲的傳播過程

超聲探頭產(chǎn)生激勵聲波信號，隨后聲波在螺栓內(nèi)傳播，經(jīng)過一定時間后聲波返回探頭部位，得到相應的回波信號，此過程如圖3所示。

(a) 2.9 μs

(b) 4.5 μs

(c) 6.94 μs

(d) 11.93 μs

圖3(a)對應2.9 μs時的聲場快照，此時可明顯觀察到聲波存在直達縱波、邊緣縱波、邊緣橫波，直達縱波信號較強、傳播速度較邊緣橫波快。圖3(b)對應4.5 μs時的聲場快照，此時直達縱波到達螺栓的中間部位，邊緣橫波則剛進入螺桿；進入螺桿后的直達縱波會在螺桿表面產(chǎn)生一定的波型轉(zhuǎn)換，得到反射縱波和反射橫波；在聲波前進過程中，反射縱波與反射橫波將不斷產(chǎn)生，由于橫波聲速較慢，反射橫波將會與直達縱波逐步拉開距離。雖然聲波在螺栓內(nèi)的傳播中產(chǎn)生較為復雜的波型轉(zhuǎn)換，但大體上可認為聲的傳播過程是縱波經(jīng)螺栓底部反射經(jīng)一定時間后到達探頭部位，形成回波信號，如圖3(c)、3(d)所示。如果對比圖3(b)、3(c)中的直達縱波，可發(fā)現(xiàn)其波形特征發(fā)生了一定變化，這一變化與縱波在螺栓側(cè)壁的波型轉(zhuǎn)換有關(guān)。從聲波在螺栓中的傳播過程可知，聲彈效應引起的超聲傳播時間變化量應該主要與聲波傳播覆蓋范圍內(nèi)的螺栓應力狀態(tài)相關(guān)。

3.3 超聲傳播的聲時差

改變螺栓的軸向載荷大小，分別獲取超聲探頭的回波信號，可發(fā)現(xiàn)隨著軸向應力的不同，超聲信號在傳播時間上會產(chǎn)生微小的變化。

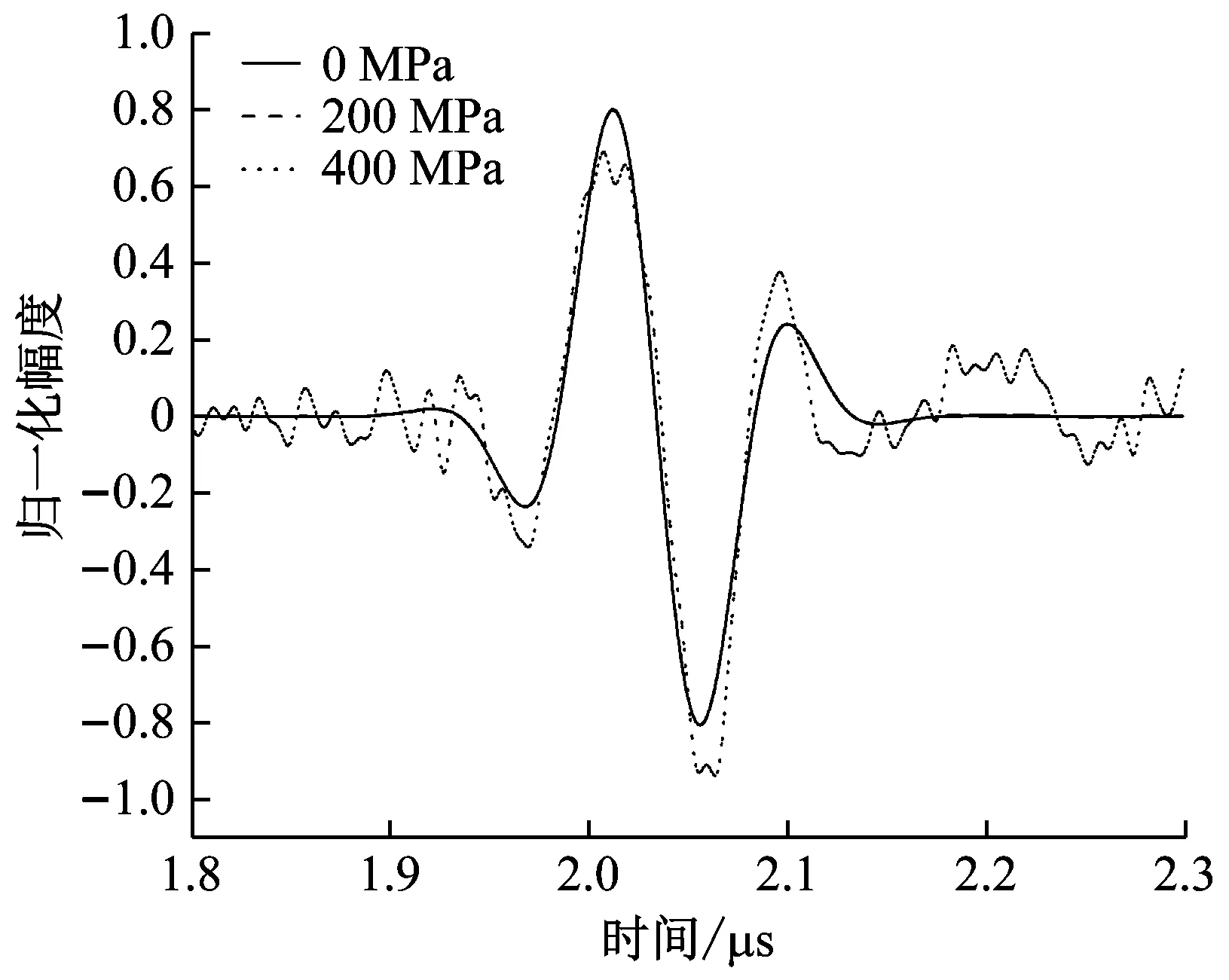
有限元計算時設(shè)定螺栓材料為表1中的材料1，設(shè)定9種不同的螺栓軸向應力狀態(tài)：F以50 MPa的間隔從0增加到400 MPa。在F分別為0、200 MPa、400 MPa時，超聲探頭接收的回波信號對比結(jié)果如圖4所示。

(a) 激勵信號段

(b) 接收回波段

圖4(a)所示為式(18)描述的激勵信號波形。F<300 MPa時，有限元計算得到的激勵信號段波形幾乎完全一致；而F300 MPa后，波形信號會出現(xiàn)一定的跳動，跳動幅度隨施加載荷的增加而變大；將400 MPa時的波形與0、200 MPa的波形進行對比顯示，可以明顯看到載荷增大所引起的信號跳動，不過波形的大致特征基本保持不變。

從圖4(b)可知，在軸向拉應力的影響下，接收回波的傳播時間有所增加。與圖4(a)類似，F(xiàn)增加到400 MPa后，回波信號出現(xiàn)了較大的跳動；在波形特征方面，接收回波與激勵脈沖波有所差別。以波形過零點對應的時刻作為參考點，可知，F(xiàn)為200 MPa、400 MPa時聲波的傳播時間比未受拉伸載荷時分別增加了29.7 ns、60.0 ns。在軸向拉應力作用下，超聲傳播時間有所增加，這一方面緣于螺栓工件的伸長，另一方面則緣于應力作用下超聲聲速的降低，而聲速變化是主要的影響因素。

在不同的軸向拉伸載荷作用下，螺栓底部回波信號會出現(xiàn)有規(guī)律的延時：隨著螺栓軸向載荷的增大，底部回波在時間上漸次錯開。對材料1的螺栓而言，軸向載荷的增量為100 MPa時，對應超聲信號的傳播時間差則約為15 ns。

3.4 夾緊長度對聲彈效應的影響

如前所述，影響螺栓聲時變化的因素中有一項是未受應力時超聲在工件內(nèi)的傳播時間；計算此時間時并不能直接使用螺栓的實際長度，而應該使用受載荷較均勻的一段螺栓長度。因此，對螺栓施加軸向載荷的夾緊長度有所不同，得到的聲彈效應規(guī)律將會有所不同。

設(shè)定螺栓材料為表1中的材料1，改變圖1中施加載荷的長度參數(shù)hl，利用有限元方法計算得到了不同夾緊長度下螺栓受軸向載荷影響所表現(xiàn)出的聲彈效應規(guī)律，如圖5所示。圖中聲時差的計算同樣以回波信號過零點作為基準(參見圖4(b))，可明顯看出螺栓在受到軸向載荷作用下表現(xiàn)出的聲彈效應，聲時差與軸向載荷大小符合線性關(guān)系。夾緊長度參數(shù)hl在2 mm、5 mm時，聲彈效應線性關(guān)系變化并不明顯，直線的斜率相差不大，保持在0.15左右；而夾緊長度參數(shù)hl在10 mm時，則使聲彈效應線性關(guān)系產(chǎn)生了較大變化，直線的斜率不到0.14，與前兩條直線差別明顯，這將為后續(xù)的應力測量帶來較大差異。以加載前后聲時差達到30 ns為例，根據(jù)圖5中的線性模型可確定出對應的拉伸載荷分別為195.4 MPa、200.6 MPa、220.4 MPa；夾緊長度參數(shù)為2 mm、5 mm時，根據(jù)線性模型確定出的拉伸載荷差值僅為5.2 MPa；而夾緊長度參數(shù)為2 mm、10 mm時，根據(jù)線性模型確定出的拉伸載荷差值則增加到為25 MPa，按夾緊長度為5 mm時的應力作真實值，忽略夾緊長度參數(shù)的不同將會使測算值的偏差大于12%。因此，基于聲彈效應測量螺栓軸向應力時，準確測定線性系數(shù)非常重要。

對夾緊長度參數(shù)影響聲彈效應現(xiàn)象的原因進行了分析：由于夾緊長度參數(shù)的不同，改變了螺栓工件內(nèi)部的應力狀態(tài)分布。施加軸向載荷F為250 MPa時，在不同夾緊長度下，螺栓所受的拉應力狀態(tài)如圖6所示(等值線數(shù)字代表應力值，單位為MPa)。

圖5 夾緊長度對聲彈效應線性關(guān)系的影響

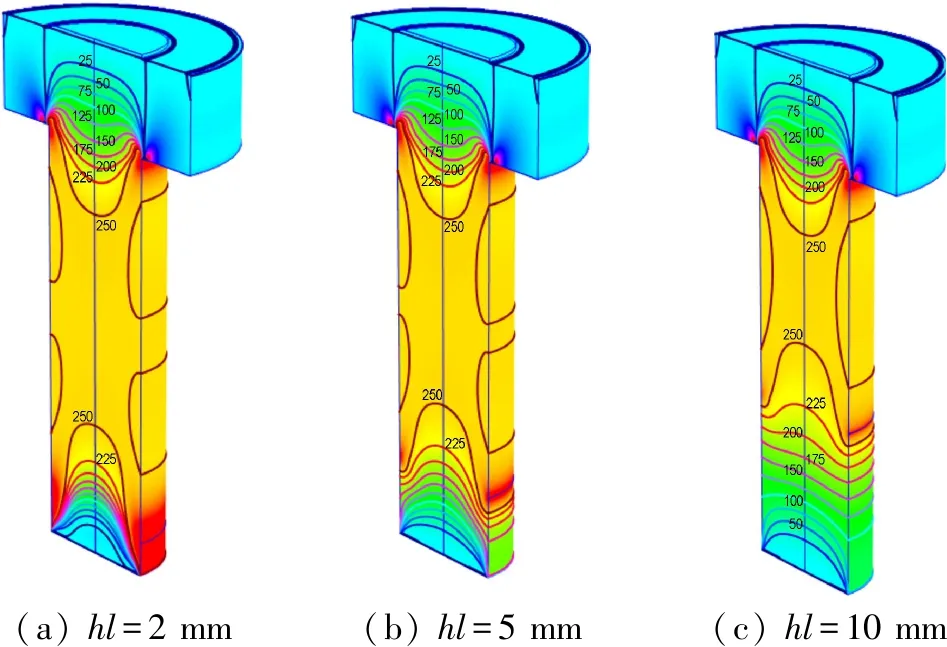
(a) hl=2 mm(b) hl=5 mm(c) hl=10 mm

圖6 夾緊長度參數(shù)對拉應力狀態(tài)的影響

Fig.6 Influence of clamp length on stress distribution in the bolt

直觀來看，夾緊長度參數(shù)hl為2 mm、5 mm時，螺栓中的拉應力狀態(tài)變化并不大，兩種狀態(tài)的區(qū)別表現(xiàn)為螺栓下端因夾緊部位的不同而有所差異；而在hl為10 mm時，螺栓內(nèi)的拉應力狀態(tài)則出現(xiàn)了明顯變化，螺栓中間較為均勻的拉應力區(qū)明顯縮小，螺栓下端的應力梯度趨于平緩。如式(17)所指出的，超聲傳播的聲時差與應力大小有關(guān)；因此，在hl為10 mm時，因螺栓內(nèi)整體應力值相對較低而使超聲傳播的聲時差偏小，表現(xiàn)為圖5中對應直線的斜率減小。

3.5 螺栓材料對聲彈效應的影響

從式(17)可知，材料特性參數(shù)(彈性模量、彈性常數(shù))將對超聲傳播時間差產(chǎn)生影響，從而使聲彈效應的規(guī)律有所不同。設(shè)定螺栓的夾緊參數(shù)hl均為5 mm，設(shè)定9種不同的螺栓軸向應力狀態(tài)，分別將螺栓材料設(shè)定為表1中的材料1與材料2，利用有限元方法計算得到了不同材料所對應的聲彈效應線性關(guān)系，結(jié)果如圖7所示。

從圖7可明顯看出，因螺栓材料的不同，對應的聲彈效應線性關(guān)系明顯不同，斜率差別較大。以加載前后聲時差達到30 ns為例，根據(jù)線性模型確定出對應的拉伸載荷分別為200.6 MPa、252.1 MPa，兩者差值可達51.5 MPa。

圖7 螺栓材料對聲彈效應線性關(guān)系的影響

Fig.7 Influence of material parameters of the bolt on acoustoelastic effect

依據(jù)表1中的材料特性參數(shù)，可知材料2所對應的彈性模量E、聲彈系數(shù)Al分別為2.0×105MPa、-0.010 7 GPa-1，材料參數(shù)帶來的聲時差影響系數(shù)為1.57×10-5MPa-1；未受應力時超聲傳播速度為6 182 m/s，夾緊長度為23.28 mm，則聲傳播時間t0為7.8 μs，根據(jù)式(17)可知聲傳播時間差(ns)與螺栓應力(MPa)間的線性系數(shù)為0.118——此系數(shù)與圖7中表示材料2的聲彈效應線性關(guān)系的直線斜率具有較好的吻合性。同樣，依據(jù)表1中材料1的特性參數(shù)進行分析，彈性模量E、聲彈系數(shù)Al分別為2.09×105MPa、-0.013 9 GPa-1，材料參數(shù)帶來的聲時差影響系數(shù)為1.87×10-5MPa-1；未受應力時超聲傳播速度為5 908 m/s，夾緊長度為23.27 mm，聲傳播時間t0為7.9 μs，可知聲傳播時間差(ns)與螺栓應力(MPa)間的線性系數(shù)為0.147——此系數(shù)與圖7中表示材料1的聲彈線性關(guān)系的直線斜率也具有較好的吻合性。由上述分析可知，雖然在式(17)的推導過程中進行了一定的近似處理，但所得到的結(jié)果仍有較高的可信度。

根據(jù)式(13)、式(14)、式(15)，則可進行更為精確的解析求解計算；將解析計算結(jié)果與有限元計算結(jié)果進行對比分析，相關(guān)情況如表2所示。

表2 解析計算與有限元計算結(jié)果對比

從聲彈效應表現(xiàn)出的線性關(guān)系的斜率來看，有限元計算結(jié)果與解析計算結(jié)果幾乎一致。在進行表2的解析計算時，需要給出等效的螺栓長度，此長度與有限元計算時的螺栓應力狀態(tài)相對應。等效螺栓長度的計算方法為：獲取有限元計算得到的螺栓應力數(shù)值，在聲波傳播覆蓋范圍(8×30.9 mm)內(nèi)計算出總的拉應力值，將此值除以施加的拉伸載荷，即可得到受力均勻的等效螺栓長度。以圖6(a)為例，聲波傳播覆蓋范圍內(nèi)的平均拉應力值為195.9 MPa，螺栓長度為30.9 mm；考慮應力因素對聲時的影響是累加的，螺栓受到平均拉應力為250 MPa，則其等效長度為24.215 mm。從表2中的對比數(shù)據(jù)可看出，有限元計算結(jié)果與理論分析預期非常吻合。此外，也說明螺栓內(nèi)部應力狀態(tài)對于超聲傳播聲時變化存在疊加影響；可通過一個轉(zhuǎn)換系數(shù)，將螺栓內(nèi)部復雜的應力狀態(tài)轉(zhuǎn)換為應力均勻狀態(tài)；對同一螺栓而言，這一轉(zhuǎn)換系數(shù)會隨著加載長度不同而發(fā)生變化，在實際測量時應對此足夠重視。

與理論解析方法相比較，有限元方法適用性更廣，它可獲取更多的定量信息，如螺栓的受力狀態(tài)、超聲波信號的傳播與接收特征、超聲波信號如何受相關(guān)因素的影響等。

3.6 有限元計算結(jié)果與實驗對比

對照有限元計算模型，選取M8的螺栓進行實驗，螺栓的總長為30.4 mm，中徑為7.188 mm。螺栓材料為40CrNiMoA，性能試驗時拉斷螺栓需要39 kN(961.1 MPa)左右的載荷。聲彈效應實驗在螺栓拉伸的同時進行，螺栓的加載力值以2 kN的步距從0增加到16 kN(394.3 MPa)。

拉伸試驗工裝分為上下分離的兩部分：上部分工裝用于安放螺栓，螺栓穿過一個環(huán)形墊塊后下表面與墊塊接觸；下部分工裝用于擰入螺栓螺紋部分，擰入長度為7.5 mm。超聲檢測探頭中心頻率為10 MHz，其晶片直徑為8 mm；探頭底部有磁性，能夠穩(wěn)妥地吸附于螺栓頭部。拉伸試驗前，使用傳感器測量螺栓的溫度為15.2 ℃。

使用DPR300信號發(fā)生器對超聲探頭進行激勵，高通、低通濾波參數(shù)分別為1.0 MHz和22.5 MHz，衰減為30 Ω。采用采集卡將超聲波形信號進行數(shù)字化處理，采樣率為1 GHz。編寫了超聲信號處理分析軟件，可對聲波的過零位置進行實時分析處理，從而得到螺栓受拉狀態(tài)下超聲傳播時間的變化；采用多次平均的方法降低隨機噪聲對處理結(jié)果的影響，波形平均次數(shù)為256次，聲時的測量精度優(yōu)于0.2 ns。

對螺栓拉伸時，由程序控制拉伸載荷大小(0～16 kN)與保載時間(40～50 s)。在螺栓拉伸的同時，對獲取的超聲信號進行實時處理，分析回波信號的過零時刻；以未加載狀態(tài)下超聲波形的過零時刻作為基準，可計算得到不同拉伸載荷下超聲傳播的聲時差，結(jié)果如圖8(a)所示。由圖8(a)可知，不同載荷下超聲傳播的聲時變化非常有規(guī)律，聲時差能夠定量指示出螺栓拉伸狀態(tài)的不同。在拉伸載荷達到12 kN時，超聲傳播聲時差出現(xiàn)了小范圍的波動(波動幅度1.5 ns)，但在隨后的拉伸過程中這一現(xiàn)象并未再出現(xiàn)。

對圖8(a)的數(shù)據(jù)進行處理，可獲取螺栓在軸向拉應力作用下超聲聲時差與載荷大小間的線性關(guān)系，結(jié)果如圖8(b)所示。對試驗數(shù)據(jù)點進行直線擬合，可知聲時差(ns)與軸向載荷(MPa)間的線性系數(shù)為0.164 7；軸向載荷變化量為100 MPa時，超聲回波信號會表現(xiàn)出16.47 ns的時間差值。與有限元計算的結(jié)果對照，螺栓拉伸試驗時聲彈效應的線性關(guān)系有所不同，其主要原因應是數(shù)值計算時的材料參數(shù)與真實材料參數(shù)間存在差異；但在聲彈效應的線性規(guī)律方面，有限元計算結(jié)果與試驗結(jié)果相一致，均表現(xiàn)為：在軸向拉應力作用下，超聲波信號在傳播時間上發(fā)生一定間隔的延時，回波的延時量與軸向載荷大小呈現(xiàn)良好線性關(guān)系。

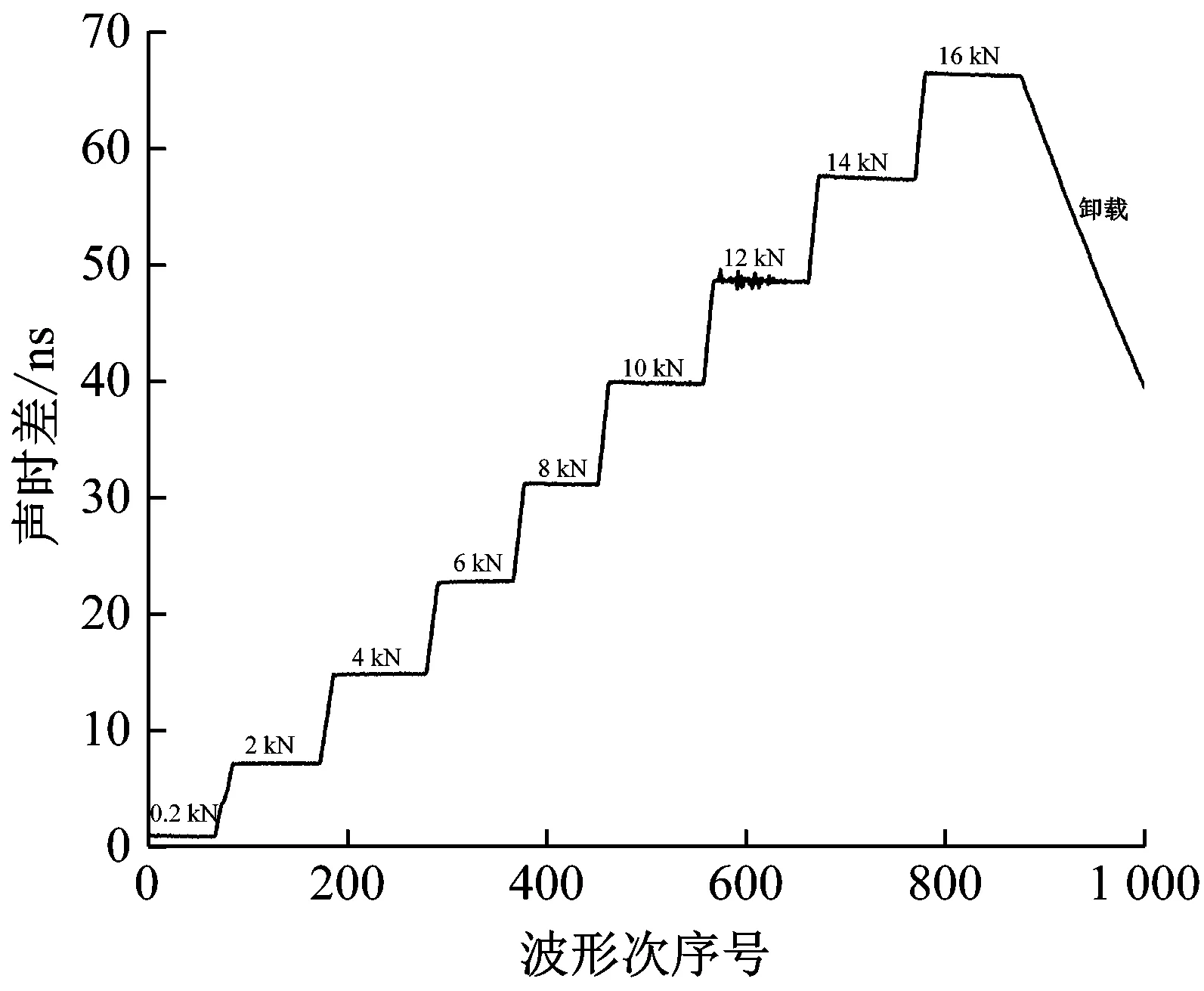
(a) 聲時差變化曲線

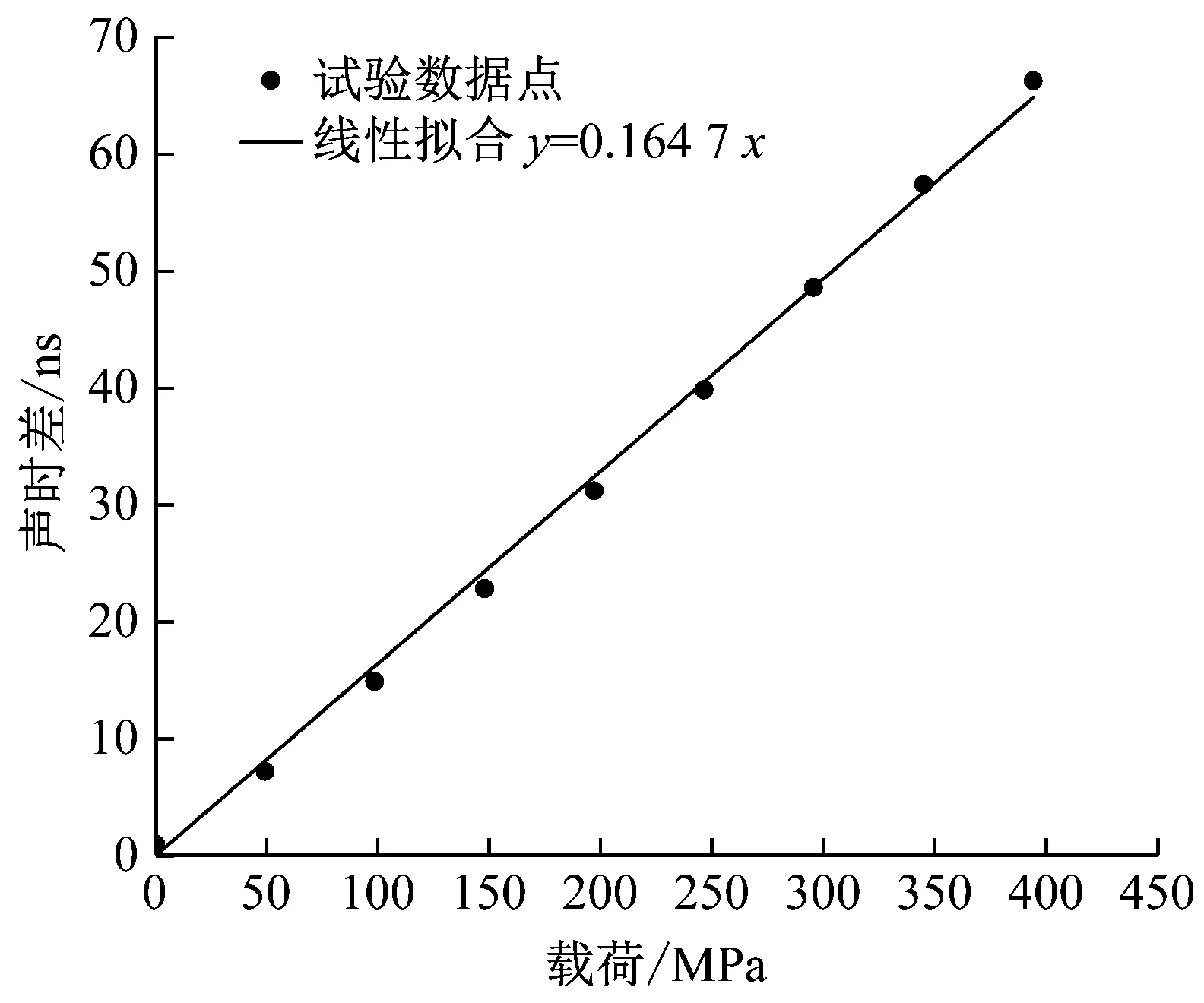
(b) 聲時差與軸向載荷間的關(guān)系

除拉伸試驗外，針對螺栓還進行了扭矩加載試驗。在不同大小的扭矩載荷下，超聲聲彈效應也非常明顯，聲時差與扭矩載荷間同樣存在良好的線性關(guān)系。因此，對用螺母擰緊的螺栓而言，利用聲彈效應評估螺栓的拉緊狀態(tài)是切實可行的，但實際應用前還需要考慮多因素的影響去構(gòu)建精確測量模型，以使測量結(jié)果更準確可靠。

4 結(jié) 論

(1) 由于建模方面的限制，此前對聲彈效應進行數(shù)值分析的研究工作還有很多不足。通過對聲彈效應進行理論分析，借助有限元計算方法，本文較好實現(xiàn)了聲彈效應的數(shù)值計算分析：使用超彈性材料構(gòu)建了螺栓模型，通過前后關(guān)聯(lián)的兩個研究步驟，獲取了螺栓在軸向應力作用下超聲傳播的波形信號。

(2) 有限元計算結(jié)果表明，螺栓軸向載荷的改變，使超聲信號在傳播時間上相應地產(chǎn)生微小的變化量；隨著軸向載荷的不斷增加，超聲回波在時間上逐步錯開。螺栓在軸向載荷作用下表現(xiàn)的聲彈效應，與螺栓材料、螺栓夾緊長度等因素相關(guān)，超聲在螺栓受載前后的聲時差受到聲傳播范圍內(nèi)應力狀態(tài)的綜合影響。

(3) 在聲時差的定量表征方面，有限元計算結(jié)果與解析計算所得結(jié)果吻合良好，由有限元計算的應力狀態(tài)可推導出受均勻載荷作用的螺栓長度；在螺栓加載的實驗中，明顯觀測到了超聲波在信號傳播時間上的漸次變化，符合有限元計算的分析結(jié)論。所建立的超聲法測量螺栓軸向應力的有限元模型，可針對特定檢測配置獲取相應的超聲時域信號，能為檢測方法分析、專用儀器研發(fā)提供有價值的技術(shù)指導。