二自由度參數振動自由響應逼近

黃迪山， 劉 成， 張 波

(上海大學 機電工程與自動化學院，上海 200072)

由于系統參數(質量、阻尼和剛度)的周期時變性，許多系統的動力學建模可以采用周期系數的二階微分方程組描述，這在力學上被稱為參數振動系統。參數振動系統的穩定性、響應預測和控制策略是研究參數振動的基本問題。在以往對參數振動穩態響應求解的研究中，常用解析方法有Hill法[1]、攝動法[2]、平均法、Floquet理論[3]、Sinha Chebyshev多項式法[4]等。另外對參數受迫振動響應的計算方法，還包括David等的傳遞矩陣法[5]、Floquet特征向量的線性組合[6]、改進的直接譜分析法[7]，IHB法進行非線性振動求解，多尺度法求振動響應[8]等。

對于參數系統定性、定量分析，以上方法雖然取得了重要進展，但是大多數方法對系統響應逼近不能完全地進行解析分析，導致一些非線性動力學特征仍然有可能被隱藏。在科學和工程應用中，用傅里葉級數表示的響應在故障識別與診斷、結構健康監測中十分便捷。尤其是在對橫向裂紋轉子、齒輪嚙合的周期性剛度問題，參數振動響應的三角級數逼近是非常重要的[9]。

為了證實線性參數激勵系統的理論結果，Han等[10-11]和Chen等[12]開發了受電磁剛度激勵的懸臂梁，觀察到參數振動的自由響應，驗證了自由響應譜是由固有頻率、及一系列固有頻率與參數頻率線性組合的重要動態特性。

調制反饋[13]模型成功地應用于參數振動受迫響應，給出了外界激勵和參數激勵共同作用下的響應。Huang等[14]給出了單自由度參數振動自由響應的三角級數逼近。本文將利用調制反饋分析法，討論二自由度參數振動的自由響應求解，并得出簡明的結論。本文所提出的矩陣三角級數逼近法是將調制反饋概念，從單自由度拓展到二自由度參數振動系統，引入歸一化模態，計算得到參數振動模態以及系數矩陣，系數矩陣事實上是諧波組合共振時的衍生模態。當調制指數足夠大時，衍生模態的影響不可忽略。

1 自由響應形式

對二自由度的剛度參數周期激勵系統，其動力學方程為

(1)

(2)

式(2)將二自由度的參數振動問題演變為圖1所示的一個含調制單元的反饋系統。該系統是由一個二自由度線性系統和一個調制環節組成。系統的輸出X(t)是所關注的參數振動自由響應。

圖1 調制反饋系統示意圖

對二自由度剛度周期激勵系統的自由響應而言，每個振蕩頻率ωsi(i=1,2)都將產生頻率裂解現象(見圖2)，系統將瞬間裂解出無窮多個頻率組合分量。

圖2 系統頻率裂解瞬間過程示意(t≥0,Δt→0)

因此，系統自由響應是主振蕩頻率ωsi和參數激勵頻率ω0的一系列線性組合，其自由響應表示為以下矩陣三角級數

X(t)=X1(t)+X2(t)=

(3)

由于反饋回路存在，系統主振蕩ωsi與固有頻率ωni是不相等，但主振蕩頻率ωsi分量分布在系統固有頻率ωni的附近；從總體上說，由于二自由振動系統中的模態具有低通濾波的功能，當系數k→∞時,諧波成分矩陣Ck→0、Dk→0。因此，二自由度參數振動自由響應的求解問題就轉化為式(3)中系數矩陣Ck、Dk和主振蕩頻率ωsi(i=1,2)的確定。

2 響應解確定

2.1 主振蕩頻率ωsi

應用歐拉公式cos(ω0t)=(ejω0t+e-jω0t)/2，式(1)可轉化為

(4)

設式(4)的解為

(5)

式中:Ek為2×1矩陣。

將X(t)代入式(4)，整理得：

(6)

對式(6)應用諧波平衡，可以得到無窮多個由系數Ek組成的線性方程

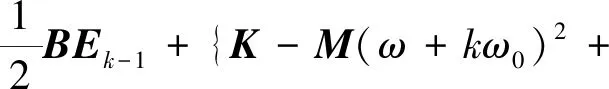
(7)

(k=-∞,-n+1,…,-1,0,1,…,n-1,∞)

引入記號

(8)

Ωk=K-M(ω+kω0)2+jC(ω+kω0)

(9)

將系數Ek組成的線性方程組裝在一起，形成無窮階的線性代數方程組, 稱裂解協調代數方程組。當階數取2n+1時，方程表達為

(10)

當n→∞時，系數矩陣E-n-1→0和En+1→0。因此，將等式(10)記作

W1E=0

(11)

式中:W1為一個復分塊矩陣。齊次方程(11)若要有解，充要條件是矩陣W1行列式等于零，則特征方程

det(W1)=0

(12)

對于二自由度參數振動系統，存在復根ωi=ωsi+jδi，ωsi為主振蕩頻率，δi為衰減因子。

特征方程式(12)求解可獲得4×(2n+1)個根。由于主振蕩頻率主要集中在系統固有頻率ωn1,ωn2附近，考慮反饋環節影響，從特征方程所求得的根值中選取接近于并小于系統第i階固有頻率ωni的值作為主振蕩頻率ωsi(i=1, 2)。

同理設：

(13)

其中Fk為2×1矩陣，將式(13)的X(t)代入式(4)，得到與式(7)類同的諧波平衡方程，將系數Fk組成的線性方程組裝在一起，可得到式(14)

(14)

令：

det(W2)=0

(15)

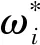
2.2 系數矩陣

系數矩陣C0和D0是與振蕩模態有關的復矩陣。矩陣C0和D0是2×2階矩陣。

在式(10)中

其中r1是向量(Γ12Γ22)T,r2是向量(Γ21Γ22)，r3是向量(Γ11Γ21)T。

設歸一化模態

(16)

因此，求得模態矩陣C0和系數矩陣Ck為

(17)

(18)

通常系數矩陣Ck是一個復矩陣。

矩陣Dk和Ck具有相同的求解過程， 可求得模態矩陣D0和系數矩陣Dk為

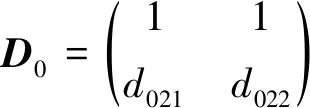
(19)

(20)

矩陣Dk與矩陣Ck互為共軛。

2.3 方程通解

在求得ωi(i=1,2),系數矩陣Ck，Dk(k=-n,-n+1,…,-1,1,…,n-1,n)，則自由響應通解可以表示成：

(21)

式中:p1,p2,q1,q2為任意常數。

2.4 初始條件

設參數振動初始條件為

X(0)=[x1(0)x2(0)]T

(22)

(23)

將初始條件式(22)和式(23)分別代入式(21)得到

(24)

X′(0)

(25)

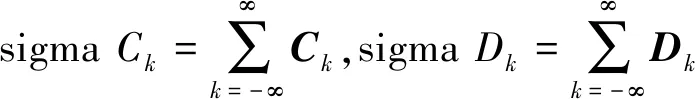
式(24)和式(25)可寫成

(26)

(27)

可得出p1,p2,q1,q2

(28)

3 數值算例與結果分析

3.1 耦合倒立雙擺系統自由響應模型

在直升機前行運動中，其旋翼葉片會不斷受到時變的載荷力及力矩的作用從而引起參數振動問題。針對直升機機翼的動力學模型，Sinha等[15]進行了簡化處理，建立如圖3所示的耦合倒立雙擺系統模型。

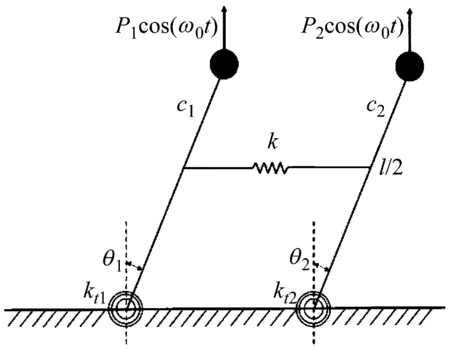
圖3 耦合倒立雙擺系統

其中雙擺與固定基礎之間由彈性系數為kt1和kt2的扭彈簧連接，雙擺桿中間位置由彈性系數為k的彈簧連接而發生耦合，擺桿轉動過程中存在阻尼c1和c2，擺桿頂部存在集中質量m，集中質量位置分別受到時變載荷P1cos(ω0t)和P2cos(ω0t)。此時，該參數振動系統的運動方程為

P1cos(ω0t)lsinθ1=0

P2cos(ω0t)lsinθ2=0

(29)

由于角度θ1、θ2均為小量，計算中可近似sinθ1≈θ1，sinθ2≈θ2。為了便于分析，對式(29)無量綱化，再引入下列參數

式(29)簡化的無量綱的微分方程

(30)

對比式(30)，在參數振動方程(1)中設置參數，令ω0=10，β1=β2=0.3。

則系數矩陣

3.2 矩陣三角級數求解

當系統在無參數激勵的情況下，得到線性方程的固有頻率

ωn1=13.004 0+j0.153 6,ωn2=50.860 7+j0.246 3，

模態矩陣

對式(16)的系數矩陣取47階方陣(k=-28,…,18)。根據所述計算過程，編制MATLAB程序，得到式(29)的振蕩頻率

ω1=12.417 9+j0.154 1

ω2=50.644 3+j0.245 9

將ω1和ω2分別代入式(16)， 可得到模態矩陣C0和系數矩陣Ck

同理，求出模態矩陣D0和系數矩陣Dk

令初始條件

(31)

通過式(28)得到p1,p2,q1,q2。

對算例進行自由響應計算，起點為0，設步長0.000 1，總時間10 s，得到參數振動響應的時間歷程、頻譜和相圖,如圖4(a)～圖4(c)所示。

4 討 論

4.1 龍格-庫塔法

為了驗證所述方法，用四階龍格-庫塔法(使用MATLAB ode45)得出的自由響應時間歷程、頻譜圖和相圖與矩陣三角級數逼近的結果進行比較。

龍格-庫塔法在MATLAB程序仿真中，設置起點為0，步長0.000 01，控制精度為1×10-7，總時間10 s，得到系統自由響應的時間歷程、頻譜和相圖，如圖5(a)～圖5(c)所示。

通過計算結果對比可以得出，兩種方法得出的時域響應、頻譜、相圖具有高度的一致性。頻譜圖用于觀察自由響應的振蕩頻率，同時可以清楚地看到由周期參數系統所引起的頻率裂解現象。相圖用來研究瞬態響應，相圖的微小變化可以表征動力學性能變化。從相圖可以看出相空間中的波擾動，而這是由于周期參數系統頻率的裂解所引起的，即周期參數系統變化導致振蕩頻率的變化。

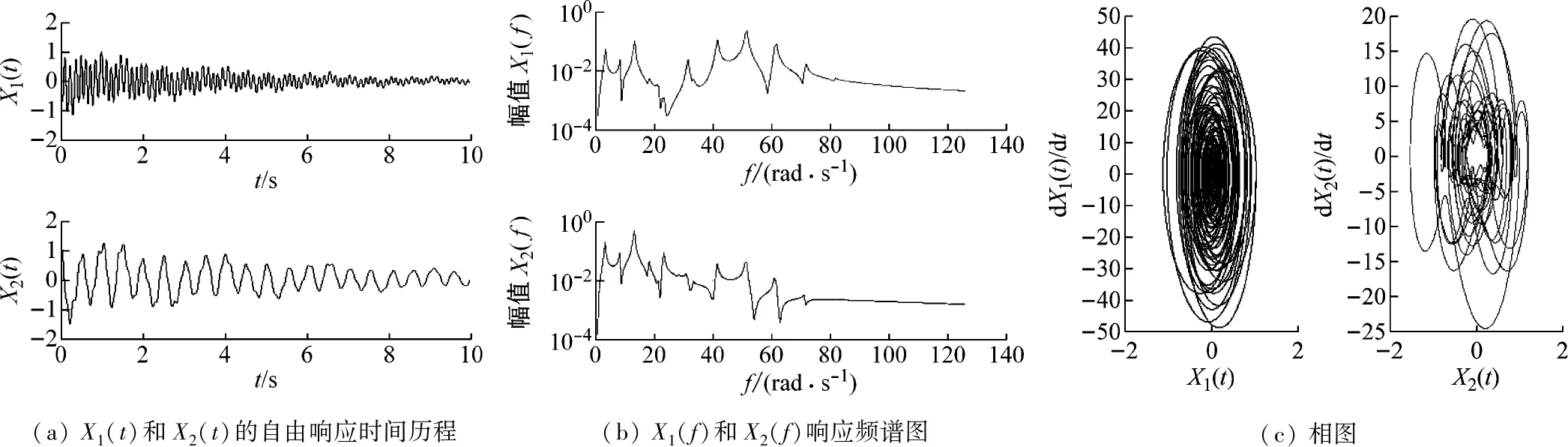
(a) X1(t)和X2(t)的自由響應時間歷程(b) X1(f)和X2(f)響應頻譜圖(c) 相圖

圖4 矩陣三角級數逼近的振動自由響應

圖5 龍格-庫塔法得到自由振動響應

Fig.5 Free response simulated by Runge-Kutta algorithm

4.2 計算誤差

為了更精確地評價上述兩種方法的準確性，引入偏差矢量ε

(32)

針對二自由度系統，ε=[ε1ε2]T，εr表示最大誤差的均方根值，即

(33)

式中:εrms1和εrms2為x1和x2的最大誤差值。

在給定的例子中，系數矩陣采用了47項(k=-28,…,18)，計算得出的最大有效誤差值εmax1=5.380 7×10-12。而龍格-庫塔法得出最大有效誤差值為εmax2=2.402 3。表1所列為兩種計算方法的計算誤差和計算所需時間對比。本文方法能提供很高的計算精度，但是計算所需時間多于龍格-庫塔法。本文方法的計算時間取決于所設的級數項數的多少。若要減少計算時間，在達到精度要求的前提下，可減少級數項數實現。

表1 兩種計算結果的比較

本文的逼近方法相比龍格-庫塔法計算誤差小。當逼近項數增加，計算誤差減小；當項數增加到一定值時，計算誤差將達到穩定，且精度趨于定值， 造成此現象的原因可能是本文方法的截斷誤差或MATLAB計算后的舍入誤差所致,如圖6所示。

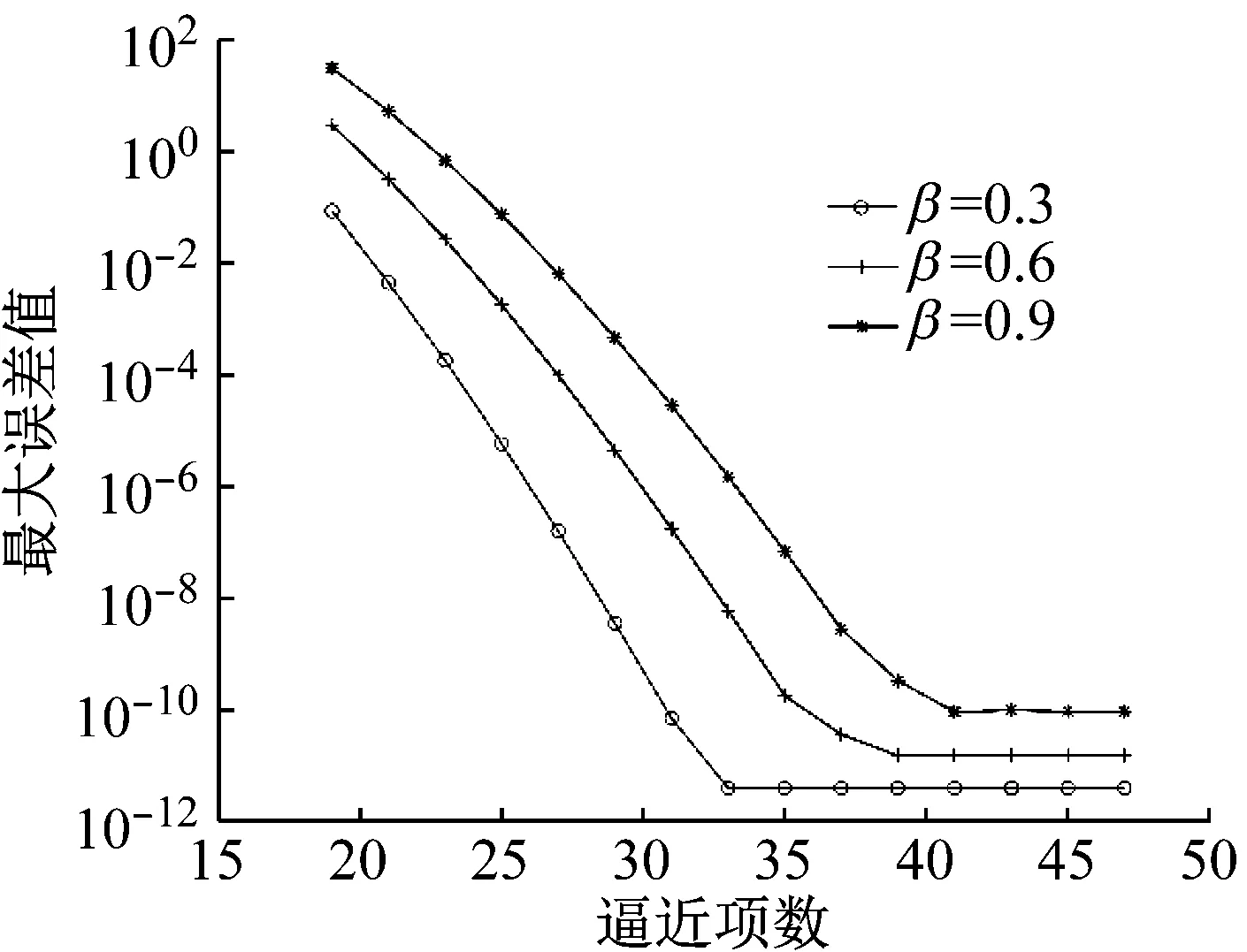
圖6 級數項數對計算誤差的影響

4.3 調制指數影響

4.3.1 主振蕩頻率

自由響應中主振蕩頻率ωs1和ωs2與調制指數β1,β2以及阻尼系數ξ有關,令β1=β2=β，① 若β=0，系統的振蕩頻率即為系統的含阻尼的固有頻率；② 當調制指數β不大時，系統的主振蕩頻率的減小趨勢不大，在工程應用中，可以將含阻尼的固有頻率替代振蕩頻率用于系統參數估計；③ 當調制指數β比較大時，系統的主振蕩頻率明顯減小，β的影響不能被忽略；④ 阻尼系數ξ對主振蕩頻率大小有影響。當調制指數β一定時，ξ增大，則主振蕩頻率ωsi(i=1,2)減小。如圖7所示。

(a)

(b)

圖7 調制指數和阻尼系數對主振蕩頻率的影響(β1=β2=β)

Fig.7 Effect of index and damping ratio on principle oscillation frequencies (β1=β2=β)

4.3.2 模態矩陣

在β1=β2=0時,參數系統的模態矩陣C0和對應的線性系統的模態矩陣P相等；在β1,β2發生變化時，模態矩陣C0會隨著β1和β2的不同而改變，如表2所示。

表2 二自由度參數系統的模態矩陣C0

5 結 論

應用調制反饋分析，給出二自由度參數振動系統的自由響應的矩陣三角級數通解，并以耦合倒立雙擺系統為例，計算了二自由度參數振動的自由響應解，得到如下結論：

(1) 自由響應的頻率是主振蕩頻率、一系列主振蕩頻率和參數頻率的線性組合，它們是ωs1+kω0和ωs2+kω0(k=-∞,-n+1,…,-1,0,1,…,n-1,∞)。參數振動系統中，組合頻率將產生諧波組合共振。

(2) 當調制指數β1=β2=0，參數系統的模態與對應的線性系統模態相同；當β1,β2發生改變時，模態將會發生改變；自由響應頻譜和相空間中的特性可以說明參數系統頻率裂解的非線性特性。

(3) 矩陣三角級數逼近法的計算精確度取決于系統矩陣的項數。當系數的項數增加，計算精度越高；調制指數大，逼近項數需增加；當項數增加到一定值，計算誤差達到穩定，而且小。

(4) 解出的系數矩陣即為衍生模態矩陣，即諧波組合共振時的振動模態。當調制指數增大時，參數振動的衍生模態不能被忽略。

(5) 阻尼系數ξ對系統的主振蕩頻率ωsi(i=1,2)的影響較大，ξ增大，則主振蕩頻率減小。

本文提出的矩陣三角級數逼近法成功地解決了二自由度參數自由振動解問題，并且通過類似方法可以求解多自由度或更高維的參數振動系統，這為解決多自由度參數振動問題提供了一個新的思路。但是，所提出的方法不適用于描述時域中的不穩定響應情況。

致謝感謝美國奧本大學教授S. C. Sinha對本研究的指導和幫助。