基于頻譜能量形態擬合的加速度積分方法研究

陳太聰， 張 奇

(華南理工大學 土木與交通學院 亞熱帶建筑科學國家重點實驗室，廣州 510641)

在結構的動力效應評價中，動位移和速度是關鍵指標之一，如場地地震位移、結構振動變形是評價結構抗震性能的重要參數[1-2]，速度響應也常用于結構阻尼評定[3]。而振動測試實踐中，通常直接測量的是振動加速度信號，而非動位移和速度信號，此時可通過對測試得到的加速度時程進行時域積分獲得位移和速度時程。但由于測量加速度往往帶有一定程度的噪聲干擾，導致時域積分得到的速度和位移會產生較大漂移，與真實響應相差甚遠。Pintelon等的研究[4]表明，采用Newton Cotes型積分公式的傳統時域積分難以獲得相對準確的速度或位移，而若采用四階Runge Kutta方法等高階積分算法，干擾噪聲會引起更大的誤差。因此如何由帶噪聲的加速度信號得到較為準確的速度和位移信息，一直是人們所關注的問題。

已有積分濾噪方法可以分為時域法和頻域法兩大類[5]。時域法中較具代表性的是多項式擬合去除趨勢項法，如陳為真等[6]將該方法用于糾正含直流分量的加速度積分響應，積分濾噪效果明顯，但顧名坤等[7]的數值試驗表明，在加速度受到復雜噪聲影響時，采用該法積分所得的響應效果不理想。因此，針對振動測試實踐中的復雜干擾環境，工程實際中更多采用的是頻域積分濾噪方法，典型的方法包括數字濾波法、低頻衰減法和頻率截止法等。

繆惠全等[8]采用數字濾波法對加速度積分所得速度和位移進行校正，可取得較好效果，但濾波的同時會造成各頻率成分的相位失真，得到的響應在時間上有延遲現象，需做相位糾正。

胡玉梅等[9]在低頻衰減算法中引入目標頻率和積分精度兩個參數，兼顧了趨勢項誤差控制和有效信息保留，但積分精度參數的取值需要多次調試。

Brandt等[10]通過對不同積分方法的對比研究，將頻率截止法作為最佳積分濾噪方法之一推薦應用。該法操作簡單，直接將帶噪加速度頻域幅值的低頻部分做置零處理，相當于理想濾波器去掉低頻成分，然后再根據加速度、速度、位移頻譜之間的比例關系，由傅里葉逆變換得到對應的時域波形。方新磊等[11]在此基礎上，又加入了高頻截止濾波，以同時消除低頻趨勢項和高頻干擾噪聲。總體上而言，頻率截止法易于實現，積分效果優越，但存在對截止頻率的設置較為敏感的問題。針對該問題，已有數值研究[12]表明，當截止頻率選擇在加速度幅值譜的主瓣或旁瓣的波谷附近時，積分得到的位移曲線與實際位移曲線的吻合程度較高，積分誤差較小。由此可見，截止頻率可參考頻譜曲線的形態來近似設置，但較為主觀。

實際上，在其它信號處理領域，已有研究通過譜曲線形態的擬合來進行信號特征提取和降噪處理。如李敏等[13]采用高斯曲線擬合光譜曲線的峰形、峰高和峰位等數據，利用擬合得到的特征參量表征光譜信息；李修文等[14]對聲發射信號的頻譜曲線做平滑處理，最后重構回時域，可以消除有色噪聲的干擾。

在上述頻率截止法和譜曲線研究的基礎上，本文提出一種結合頻譜能量形態擬合的頻域積分新思路，定義為有效頻段法，用于加速度信號的積分濾噪。該方法假設各峰值主頻臨近區域的頻譜曲線符合高斯函數分布，根據該區域內帶噪信號的累積能量變化，擬合得到相關函數參數，從而根據三倍標準差原則確定主頻有效信息的分布范圍，進而通過各有效頻段內的頻域積分和逆傅里葉變換，重構得到相應的速度和位移信號。文后通過多頻簡諧激勵和隨機激勵下的數值模擬算例，開展本文方法與頻率截止法的對比分析，以檢驗方法在不同激勵下的積分精度和抗噪性能。

1 頻率截止法的基本原理

因為本文方法是參考頻率截止法的改進研究，因此有必要先簡要介紹頻率截止法的基本計算原理。

假設按等時距Δt測量得到的帶噪加速度信號為X(n)，n=0,1,2,…,N-1，則根據離散傅里葉變換的基本原理，離散的時域加速度信號X(n)可轉換為頻域內若干離散的頻譜信號H(k)，k=0,1,2,…,N-1，其相互轉換關系為[15]

(1)

(2)

式中:N為采樣數據量;n為時刻點;k為譜線序列點。

頻率截止法的基本原理是對頻譜中的小于下限截止頻率fL和大于上限截止頻率fU的頻率成分幅值均設置為零，即認為該兩部分完全為噪聲影響，僅保留兩個截止頻率之間的信號。該方法可表達為

(3)

式中:Fs=1/Δt為采樣頻率。

由傅里葉逆變換公式可知，加速度信號在任一頻率ωk=2πkFs/N處的傅里葉分量可以表達為

a(ωk,t)=Skejωkt

(4)

式中：Sk為對應a(ωk,t)的譜系數。

當初速度和初位移分量為零時，對加速度信號分量分別進行一次積分和二次積分，可得對應頻率ωk的速度信號分量和位移信號分量為

(5)

(6)

最后結合式(1)～式(6)，可得經頻率截止后重構得到的加速度、速度和位移信號分別為[16]

(7)

(8)

(9)

最終，頻率截止法用于加速度的濾噪和積分濾噪的相關計算流程，可總結如圖1所示。

圖1 頻率截止法的積分流程圖

2 基于有效頻段的頻域積分方法

以上方法在處理含直流分量等低頻噪聲和機械、電路等引起的高頻噪聲的加速度信號積分時有較好效果，但工程測量中還會包含如環境干擾等寬頻噪聲的情況，影響上下限截止頻率之間的頻率分量，頻率截止法無法過濾該部分噪聲，最終將影響積分效果。

此時，就有必要采用一定標準，重新甄別有效的頻段范圍，可能為間隔的若干段，以替代頻率截止法中定義的單一頻段[fL,fU]，供后續頻域積分使用。本文將基于這一思路的頻域積分方法稱為有效頻段法，文中也將通過頻譜能量形態擬合的方式來確定有效頻段的分布范圍。

2.1 分段頻譜曲線形態假設

設實測加速度信號X(n)的對應頻譜H(k)包含m個峰值主頻，按從小到大的順序依次為f1,f2,…,fm。如此整個頻率范圍可按如下方式分為m段

(10)

式中:fmax為頻譜曲線對應的最大頻率，在振動測試中一般取為分析頻率，即fmax=Fa=Fs/2.56；或當fm距離Fa較遠時，也可近似取fmax=(2∶5)fm，對濾波結果的影響不大。

為了方便后續分析，上述m個頻段均進行歸一化處理，即都歸一化為范圍(0,1]。此時，假設每個頻段內的頻譜曲線符合相應的高斯函數分布[17]

(11)

式中:i=1,2,…,m；x∈(0,1]為每個頻段內的歸一化頻率；參數ai、bi和ci分別代表高斯函數的幅值、中心位置和半徑。

基于式(11)定義的頻譜分布形態，相應的每一頻段內的頻譜累積能量分布函數可由下式計算得到，

(12)

式中:erf(·)為誤差函數;Ei(x)在形態上表現為反Z型的單調遞增函數。

至此，高斯頻譜分布函數Gi(x)和頻譜累積能量分布函數Ei(x)均可用于后續的參數擬合，以確定高斯函數中的待定參數。但實際計算表明，基于頻譜Gi(x)的參數擬合結果不穩定，容易受測試噪聲水平波動的影響；而基于能量Ei(x)的參數擬合效果較好，受測試噪聲的影響小。因此，本文選用頻譜累積能量分布函數Ei(x)來進行參數擬合。

(13)

2.2 分段累積信號能量計算

在第i個歸一化頻段內，離散的加速度頻譜信號的累積能量按下式計算得到

(14)

(15)

2.3 參數擬合與有效頻段確定

基于式(15)計算得到的離散數據，用式(13)定義的非線性連續函數進行非線性擬合，迭代收斂后得到參數bi和ci，其中迭代初值可分別取為0.5和0.5。

如圖2所示為實際操作中的一個典型例子，顯示了某個歸一化頻段中計算得到的帶噪信號離散數據，以及相應擬合得到的頻譜累積能量分布曲線和對應的高斯頻譜曲線。

根據概率統計理論，高斯分布函數在均值位置左右三倍標準差范圍內的數據具有99.73%的保證率[18]，足以表征函數。因此，第i階主頻能量分布的歸一化有效頻段可按三倍標準差原則取值如下

[bi-3ci,bi+3ci]

(16)

其相應的實際有效頻段為

(17)

最終，有效頻段法的積分濾噪流程,如圖3所示。有效頻段法的實現過程與頻率截止法基本相同，然而其通過曲線擬合自動確定最佳的頻域積分范圍，減少了主頻之外的噪聲干擾。

圖2 歸一化頻段內的頻譜能量形態擬合示意

圖3 有效頻段法的積分流程圖

3 數值算例

如圖4所示為六自由度懸臂梁結構，考慮豎向振動。其各階模態阻尼比為0.01，質量陣和剛度陣為

M=diag(4 4 4 4 4 4)×105kg

圖4 六自由度懸臂梁結構模型

Fig.4 Structural model of a 6-DOFs cantilever beam

設結構的初始速度和位移均為零，考慮工程中較常見的激勵類型，在結構自由端分別施加豎向的多頻簡諧激勵和白噪聲隨機激勵，其中簡諧激勵取為

z(t)=200sin 6πt+100sin 20πt+100sin 40πt

然后按Newmark-β法求出加速度、速度和位移響應時程，作為精確參考解。在加速度解中分別加入1%、5%、10%、15%、20%和25%的白噪聲干擾作為觀測加速度。再采用有效頻段法得到速度和位移響應，以及修正的加速度響應。這里作為對比，同時采用頻率截止法中常用的低頻截止進行相關響應的積分求解，并考察不同的下限截止頻率取值，其表示為第1響應主頻f1的不同比例。最后分別與精確參考解進行對比，并采用如下定義的總體誤差指標來評價積分精度

(18)

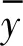
3.1 多頻簡諧激勵情況

在多頻簡諧激勵下，以質點3處的豎向響應為例，圖5給出了不同噪聲水平下兩種方法的結果精度對比，圖6～圖8分別給出了25%噪聲水平下兩種方法濾噪后的加速度頻譜對比，積分所得的位移時程對比，以及取不同下限截止頻率時的頻率截止法的計算精度。

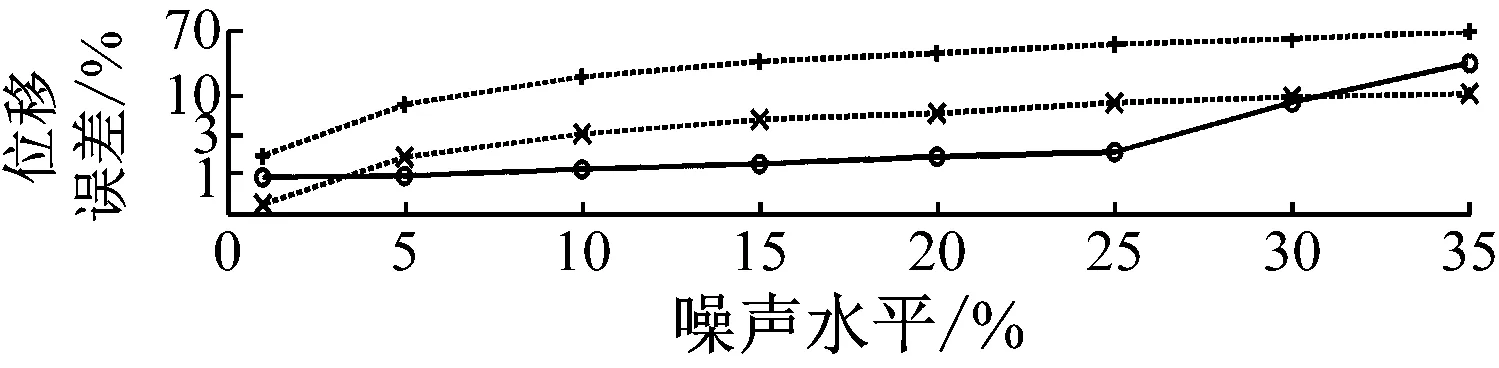
圖5 不同噪聲水平下的結果誤差

由圖5～圖8可知，在簡諧激勵作用下，

(1) 頻率截止法的計算精度，尤其是對于積分位移響應，受下限截止頻率的影響非常大，積分精度與截止頻率間滿足單調關系；同時，隨著噪聲加大，計算精度變差；

(2) 有效頻段法計算得到的三種響應，在絕大部分情況下均較頻率截止法的結果精度更高；在25%噪聲水平以下時，結果誤差均為1%～2%，即使在25%噪聲干擾下，積分位移也幾乎與精確位移重合。

圖6 25%噪聲下的濾噪后加速度頻譜

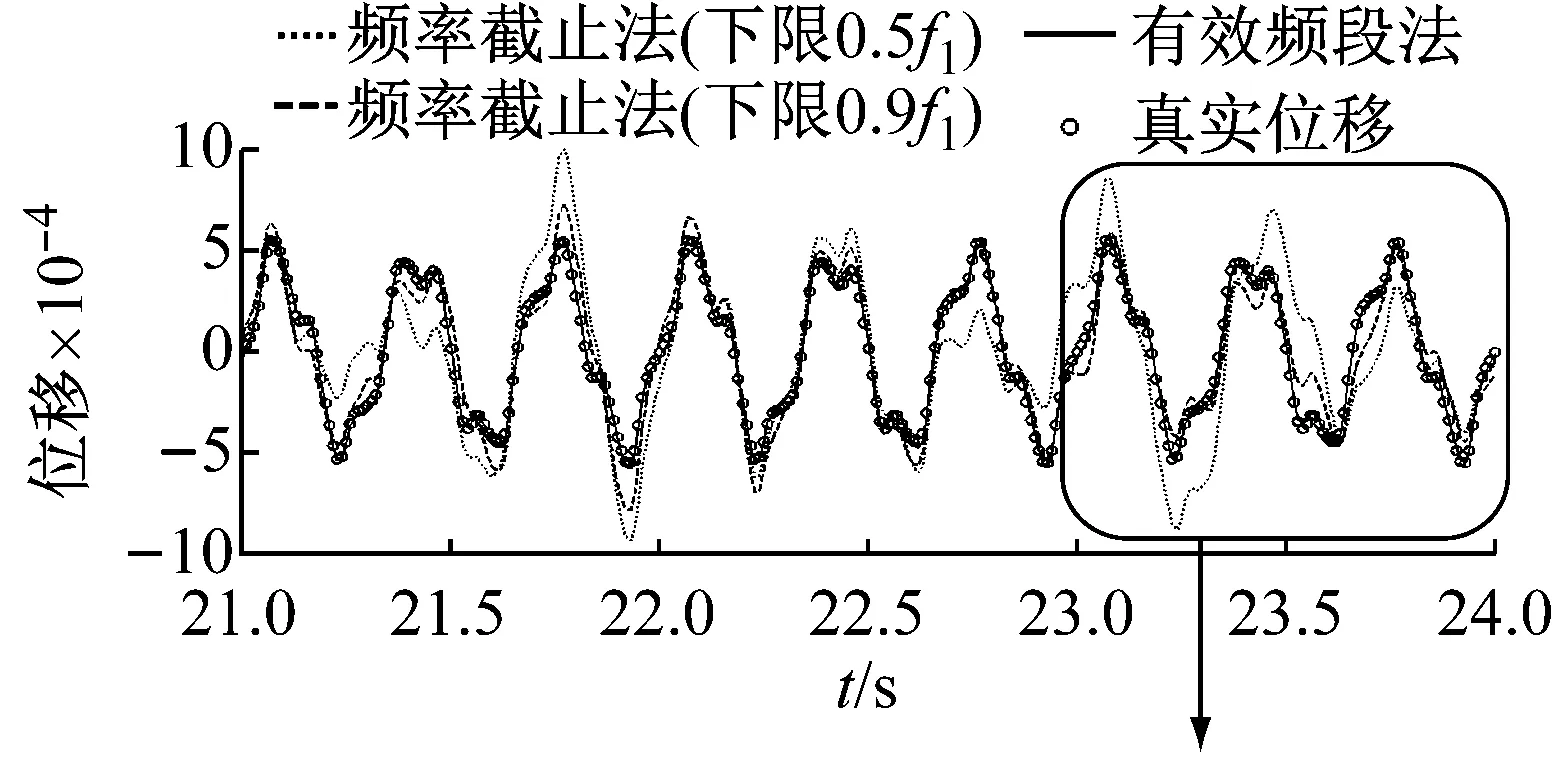
圖7 25%噪聲下的位移時程

圖8 25%噪聲下取不同下限截止頻率時的位移誤差

3.2 隨機激勵情況

在隨機激勵下，同樣以質點3處的豎向響應為例，圖9給出了不同噪聲水平下兩種方法的結果精度對比，圖10～圖12分別給出了25%噪聲水平下兩種方法濾噪后的加速度頻譜對比，積分所得的位移時程對比，以及取不同下限截止頻率時的頻率截止法的計算精度。

由圖9～圖12可見，在隨機激勵作用下，

(1) 頻率截止法的計算精度，尤其是對于積分位移響應，受下限截止頻率的影響同樣非常大，但積分精度與截止頻率間不完全滿足單調關系；同時，隨著噪聲加大，計算精度同樣容易變差；

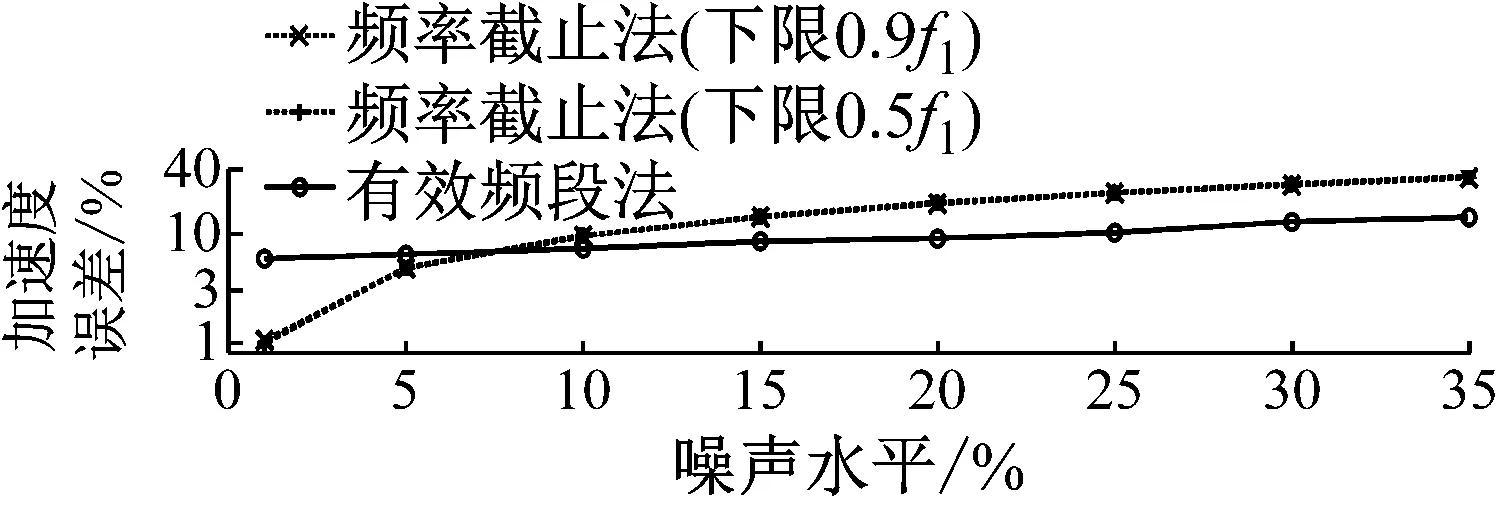
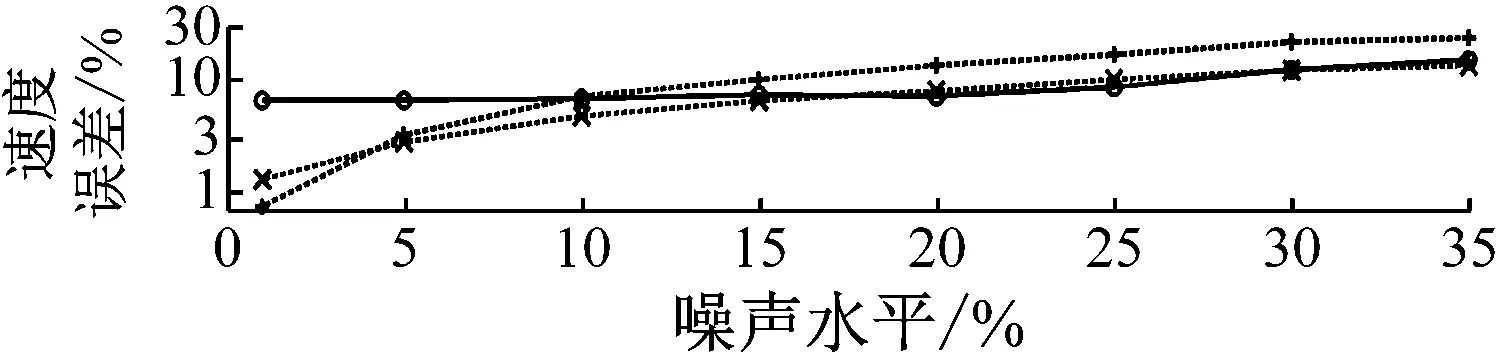
圖9 不同噪聲水平下的結果誤差

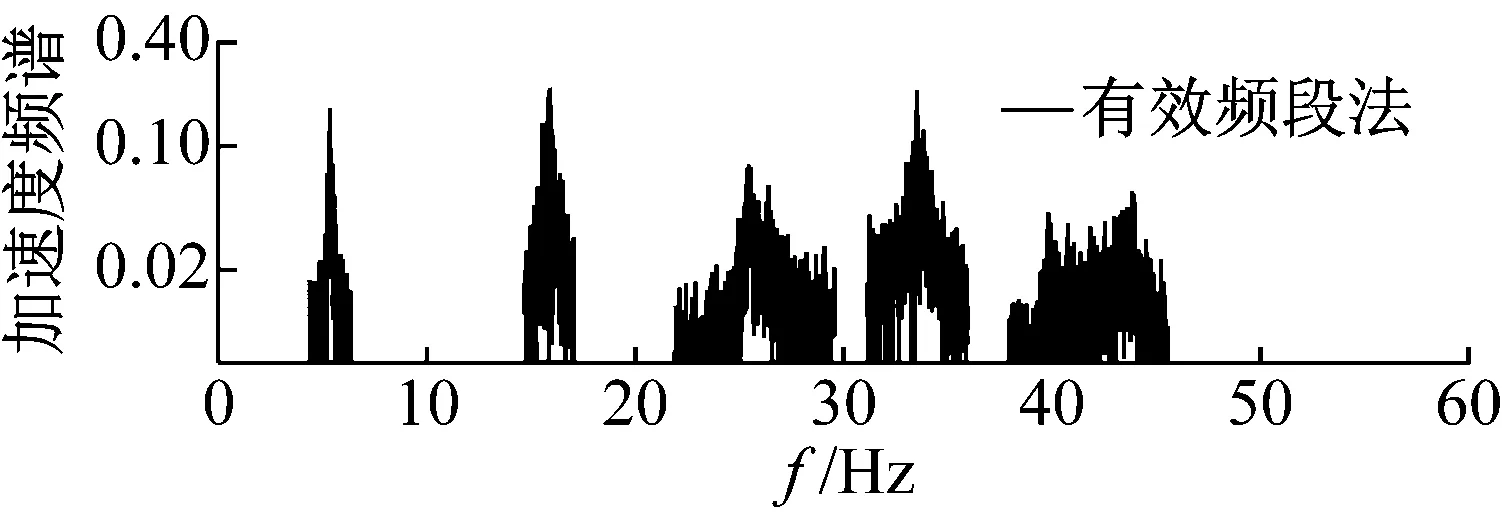
圖10 25%噪聲下的濾噪后加速度頻譜

圖11 25%噪聲下的位移時程

圖12 25%噪聲下取不同下限截止頻率時的位移誤差

(2) 有效頻段法計算得到的三種響應，在多數情況下較頻率截止法的結果精度更高或相當；在25%噪聲水平以下時，結果受噪聲水平的影響小，誤差在5%～10%間緩慢變化，即使在25%噪聲干擾下，積分位移也非常接近于精確位移。

由圖5和圖9可知，在大于25%噪聲水平的情況下，有效頻段法的積分精度會隨著噪聲加大而迅速變差。其原因不僅在于主頻處的頻譜混入了較大噪聲，噪聲能量還造成了擬合高斯函數的半徑變大，導致積分頻率范圍擴大，從而引入了更多的主頻外的噪聲影響。因此，為了保證積分結果的可靠性，建議有效頻段法在小于30%的噪聲水平下使用。

4 結 論

針對工程振動測試實踐中帶噪加速度信號的積分問題，常用的頻域積分方法如頻率截止法等雖然物理意義明確，操作簡單直接，相關參數少，但也存在參數敏感、截止頻率不易確定等不足。

本文提出有效頻段法以改進常規頻域積分方法，應用區域頻譜形態的高斯函數假定，根據頻譜累積能量曲線擬合函數參數，進而自動提取主要積分頻段信息，濾除次要頻段及其上的噪聲影響，有效避免了參數敏感性問題，并提高了積分精度和抗噪性。在應用有效頻段法時，雖然需要知道響應的主頻信息作為輸入參數，但該信息僅用于頻域初步分段，而非最終的積分頻段，因此僅需已知主頻的近似取值即可，而這些信息通常可以通過頻譜分析容易獲得。這一較低的參數要求特點也有助于有效頻段法在工程實踐中方便應用。

還需說明的是，由于應用了傅里葉變換，因此有效頻段法與頻率截止法類似，均僅適用于穩態加速度信號的積分處理，包括簡諧激勵和平穩隨機激勵的實際情況。針對非穩態加速度信號的積分處理的相關研究，仍在進行中，后續將另文報告有關結果。