考慮結構約束時油氣潤滑高速角接觸球軸承的溫升特性

陳蔚芳，鄭德星

(南京航空航天大學 機電學院，南京 210016)

以高速、高精加工為主要特征的高速加工是當代先進制造技術之一。高速數控機床是發展和應用高速加工技術的基礎，其性能取決于主軸等關鍵功能部件。角接觸球軸承結構簡單、轉速高、摩擦力矩小，可同時承受徑向和軸向雙向載荷，因而廣泛應用于高速主軸單元的支承組件[1]。熱特性是影響角接觸球軸承工作性能的關鍵因素[2]，針對軸承的生熱和熱傳遞機制已進行了廣泛的研究。

文獻[3]通過對不同類型和尺寸的軸承進行試驗，擬合出了摩擦力矩計算的經驗公式。文獻[4]研究了滾動軸承的擬動力學，采用摩擦力矩計算軸承摩擦熱，闡釋了油潤滑條件下球軸承和滾子軸承的滾動體與滾道接觸的摩擦發熱功率,黏性拖動力摩擦熱,保持架和套圈之間的摩擦熱,以及滾子端面與內圈擋邊之間的摩擦熱。文獻[5-9]在此基礎上相繼進行了生熱和散熱機理的建模研究。

當前常用的多元回歸方法、最小二乘支持向量機方法、灰色系統、OBS方法及其組合等大都基于經驗建模，較少考慮溫升機理及變化規律，因而各種影響因素很難耦合進熱特性模型中。有限元法可以模擬任意復雜的結構，求得其近似解，但存在著邊界條件難以確定的問題。熱網絡法(熱阻熱容法)是一種熱電比擬的分析方法,具有實用性強和邊界條件易于處理等優點,解決了有限元法應用于復雜系統熱分析時邊界條件難以確定的問題[10]。

文獻[11]基于球軸承DN值試驗對角接觸球軸承熱網格模型合理性進行了驗證，并引入了潤滑油比例因子。文獻[12]考慮球與溝道之間的滾滑摩擦熱,繞流阻力損失以及保持架與套圈之間的滑動摩擦熱，建立了基于油氣比較完善的角接觸球軸承的熱網格模型，但其并不適用于高速角接觸球軸承。

現基于熱網絡法，考慮高速主軸工作時結構約束,軸承的結構特性,冷卻/潤滑等氣/液特性對熱傳導,換熱和散熱特性的影響，研究油氣潤滑條件下高速角接觸球軸承的溫升特性。

1 高速角接觸球軸承生熱機制

角接觸球軸承外圈安裝于箱體或支架上，內圈安裝于軸頸隨軸同步旋轉，球在繞軸承中心軸線滾滑的同時，由于與內、外圈之間的摩擦作用而產生陀螺運動，保持架公轉的同時與球之間發生碰撞。基于角接觸球軸承的這些工作狀態，高速角接觸球軸承單元生熱包含以下部分：球與內、外溝道的滾動、滑動摩擦熱；球-潤滑劑繞流阻力損失；保持架-球碰撞功率損失；球自旋功率損失等。

1.1 球-溝道滾動摩擦熱

球與溝道之間的滾動摩擦熱為

(1)

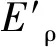
1.2 球-溝道滑動摩擦熱

根據Hamarock和Dowson點接觸彈流潤滑公式求解油氣潤滑油膜厚度為[14]

(1-0.61e-0.68k)，

(2)

式中：u為球相對滾動速度；E0當量彈性模量；E為彈性模量，ν為泊松比；k為橢圓率。

把潤滑油看作Newton流體，則油膜切應力τ為

τ=ηDz，

(3)

η=η0eαp，

Hc=hmin/Rx，

式中：Dz為剪切速率；η為潤滑劑動力黏度;p為壓力；vR為油膜兩表面之間的相對滑動速度；Hc為量綱一的中心油膜厚度。

球與溝道之間的滑動摩擦熱為

(4)

1.3 球-潤滑劑繞流阻力損失

油氣潤滑情況下，球在軸承腔體內高速運轉時會產生拖曳力。球與油氣混合物之間的拖曳效應產生的能量損失為

(5)

ρeff=Xρoil+(1-X)ρair，

式中：Fd為球的繞流阻力；ωc為球公轉速度；Dpw為球組節圓直徑；Bc為保持架厚度；CD為繞流阻力系數；ρoil，ρair，ρeff分比為油、氣和油氣混合物的密度，X為油氣比例系數[12]；moil為潤滑劑的質量流速；ω為軸承轉速。

1.4 保持架-套圈滑動摩擦熱

角接觸球軸承的保持架主要有兩類：一類是保持架有引導部；另一類是保持架沒有引導部。對沒有引導部的高速角接觸球軸承，球與保持架之間的摩擦為

(6)

式中：γ，θ，rd為定義的計算參數；mb為保持架質量；fc為滑動摩擦系數。

1.5 球的自旋功率損失

在高速條件下，球繞軸承軸線以ωc公轉，且以角速度ωb做陀螺運動，則在球與溝道接觸區內的應力為

(7)

式中：b為接觸橢圓短半軸。接觸點的相對滑動速度為

(8)

參照(4)式，對接觸區域各點的切應力及相對滑動速度的乘積積分，可得自旋功率損失為

(9)

2 高速角接觸球軸承熱傳遞

熱傳遞包括熱傳導、熱對流和熱輻射。當物體溫度處于200 ℃以下可以不考慮熱輻射。高速機床主軸負載工作時，主軸外表面的溫度在40～80 ℃之間。考慮主軸結構對軸承的約束，熱輻射對軸承的熱特性影響很小，故不予考慮。

2.1 熱傳導

在角接觸球軸承中，軸承座、套圈、軸以及球-套圈接觸區域都存在熱傳導關系。

1)套圈、軸承座和軸都是回轉體，將其視作內徑為d、外徑為D的圓筒，則熱傳導關系可視為沿半徑方向的一維熱傳導，熱阻為

(10)

式中：kD為導熱系數；L為特征長度。

2)球與溝道間的接觸為接觸尺寸遠小于軸承尺寸的Hertz接觸。考慮接觸區域尺寸和運動狀態對熱阻的影響，該部位的熱傳導可依據文獻[15]的模型計算為

(11)

Pe=Va/α，

式中：Pe為Peclet數；V為特征速度。

2.2 熱對流

在角接觸球軸承內部，熱量由軸承傳給氣/液流體，再由氣/液流體傳給軸承座等其他部件，此外軸承外表面與環境氣體之間也存在熱對流。對流換熱熱阻為

(12)

式中：A為對流換熱面積；hc為對流換熱系數；Nu為Nusselt 數。

1)當球在油氣潤滑條件下運動時，與周圍的油氣混合物之間會發生熱量交換。把球近似看作浸在無限大的油氣混合物中，忽略與套圈、保持架及其他球之間的傳熱，則球與周圍油氣混合物之間的熱對流熱阻見(12)式，Nu為[16]

(13)

式中：Re為Reynolds系數；Pr為 Prandtl 數；Tbulk為球溫度；Twall為油氣溫度；ρeff，ηeff分別為油氣混合物的密度和黏度；ηoil，ηair分別為油、氣的黏度；αd為擴散系數；Cp為比熱容。

2)套圈及保持架間充滿油氣混合物，當其高速轉動時，與油氣混合物之間發生熱交換，其傳熱關系可視為同心旋轉圓柱模型，Nu為[17]

(14)

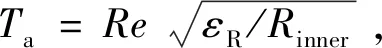
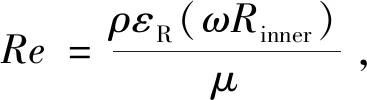
式中：εR為內外圈之間的徑向間隙；Rinner為外圈內側半徑；μ為油氣混合物黏度系數。

3)內圈側面會與油氣混合物形成熱對流，內圈側表面可以看作一個旋轉圓盤，Nu為[18]

(15)

4)伸出軸承以外的高速轉動的主軸部分也會與空氣形成熱對流關系，Nu為[19]

(16)

Re=VspindleDshaft/vair,

式中：vair為空氣的運動黏度；Vspindle為主軸表面線速度；Dshaft為主軸直徑。

5)在油氣條件下，油氣進入軸承腔體內部吸收熱量，流出軸承腔體帶走熱量，其帶走的熱量為

H=ρeffqCp(Toilair-dis-Toilair-in)，

(17)

式中：q為油氣混合物流量；Toilair-dis為油氣排出溫度；Toilair-in為油氣初始輸入溫度。

等價熱阻值為

(18)

3 熱網格模型

3.1 熱節點劃分

為便于建立熱網絡模型，對軸承的外部結構約束進行簡化(圖1)。油氣潤滑條件下，考慮高速主軸結構約束的角接觸球軸承熱網格關鍵節點劃分如圖1所示。角接觸球軸承采用通用的外圈供給油/氣方式，圖中：Q1，Q2分別為球與內、外圈之間的滾滑摩擦生熱源；Q3為球繞流阻力損失熱源；Q4為球-保持架碰撞功率損失熱源；Q5為球自旋功率損失熱。節點設置時，考慮到油/氣供給孔道尺寸較小且處于機構內部，對機構散熱和換熱影響較小，忽略其影響。節點16設置于中空主軸中心，其溫度假定與環境節點23(22 ℃)一致；徑向外表面節點11，29以及軸向外表面節點18，27溫度可由紅外測溫儀測量；遠端節點30溫度可視為常溫；外圈節點12，10溫度可通過直插式傳感器測量；為便于計算接觸熱阻，在球與內外圈接觸處各設置2個節點6，7和8，9；節點13，28分別設置于內、外圈表面；節點25，26設置于內圈側面用于計算對流換熱熱阻；節點24，17分別代表入口和出口油氣溫度；節點21設置于保持架表面。

圖1 熱網絡模型Fig.1 Thermal networks model

3.2 熱平衡方程組的建立及求解

依據Kirchhoff熱流定律，溫度梯度的熱流量為

(19)

式中:Th，Tsur-1為點、面的溫度；Rh-sur-1為熱阻。

二維溫度節點系統如圖2所示，圖中：T0為熱源溫度；T1～T4為熱源周邊溫度。依據熱流平衡原理，有

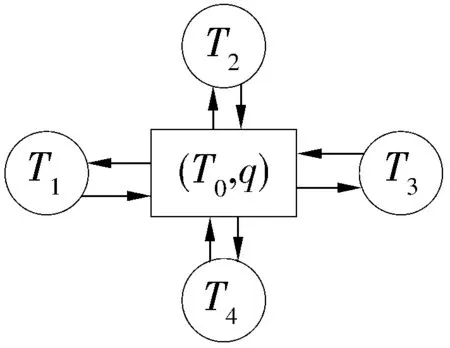
圖2 二維節點溫度系統Fig.2 Two-dimensional node temperature system

∑Qg+∑Qd+∑Qv=0，

(20)

式中：Qg為生熱量；Qd為熱傳導熱量；Qv為對流散熱量。對單個節點，其散熱量為

(21)

假設圖1熱網格模型中的任何2個節點之間都存在熱傳遞，則熱平衡方程可表達為

(22)

因熱阻矩陣與待求節點溫度有關，對于此線性方程組需采用迭代法求解。在求解時，對于不產生熱傳遞關系的兩節點間熱阻設為無窮大。文中設置節點量較多，采用Gauss-Seidel法借助MATLAB軟件進行求解，計算對象為某高速主軸前支承7009AC角接觸球軸承，相關參數見表1。

表1 熱傳遞計算參數Tab.1 Heat transfer calculation parameters

4 試驗驗證

試驗環境溫度22 ℃，油冷機設置溫度20 ℃，以節點12的溫度作為測試對象。

4.1 主軸轉速對軸承溫升的影響

在供油量0.4 mL/h，空氣流量2.5×10-3m3/s，油運動黏度22 mm2/s下，軸承溫升的仿真計算值和試驗值隨主軸轉速的變化曲線如圖3所示。

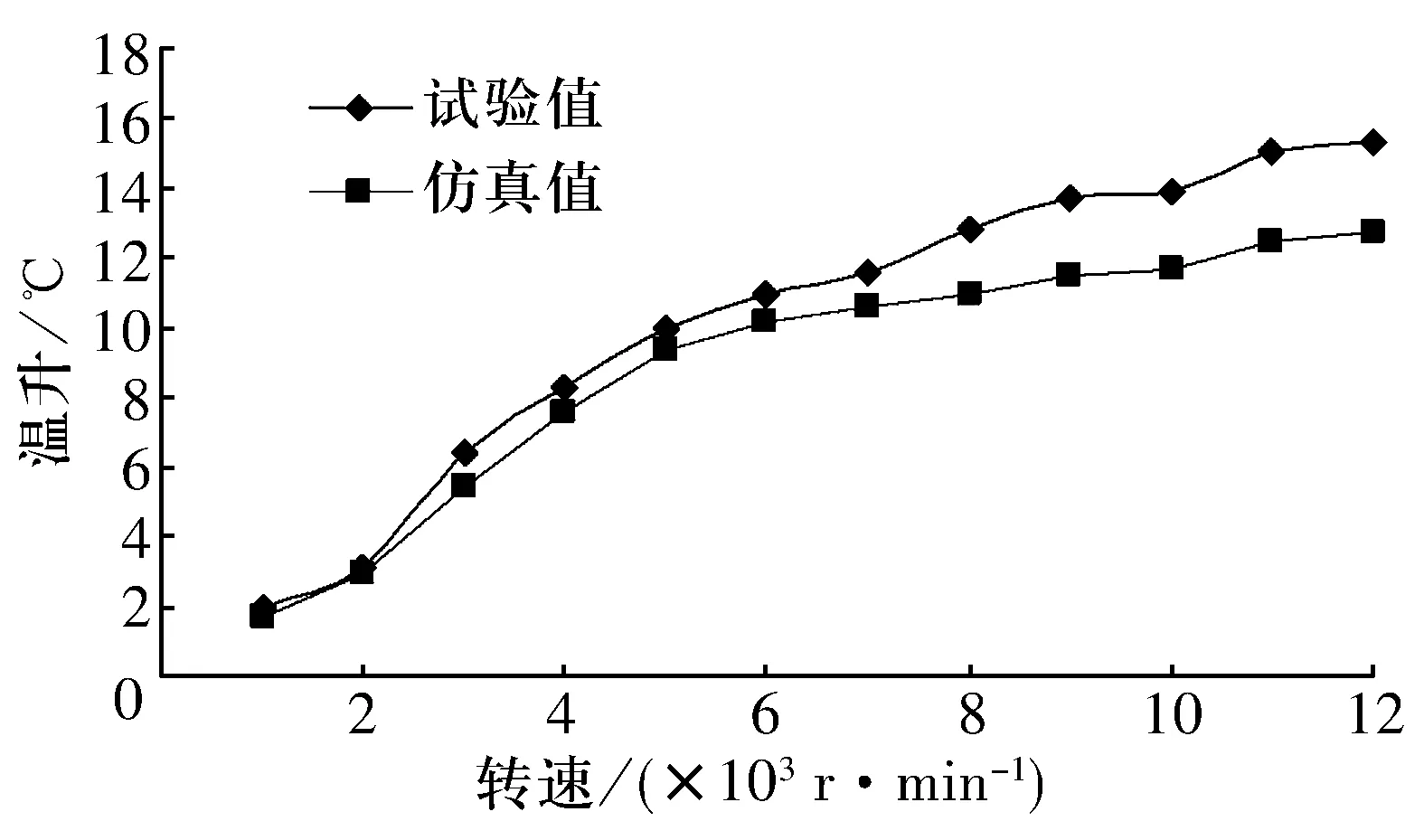
圖3 軸承溫升隨轉速的變化曲線Fig.3 Variation curve of temperature rise of bearing with rotational speed

由圖3可知，外圈溫升隨轉速變化的試驗值與仿真值整體吻合較好，溫升隨著轉速的增加而增大，在速度低于6 000 r/min時，試驗值與仿真值間的吻合度高。轉速低于5 000 r/min時，隨轉速的升高溫升增長較快；轉速高于5 000 r/min后，隨著轉速的增大溫升增長變慢,這是因為隨著轉速增大，發熱量增加,但型腔內流體之間的對流換熱增強，因此在一定程度上降低了軸承溫升。

此外，相同轉速下的試驗值大于仿真值，且隨著速度增大，試驗值和仿真值間的誤差逐漸增大。這是因為隨著轉速的增大，球-潤滑劑繞流阻力增大，生熱增大。該項生熱實際上位于球表面，自球表面向外傳遞，而仿真時此熱源位于球中心；仿真試驗中沒有全面考慮兩部件接合面的接觸熱阻，僅考慮了球-套圈之間的接觸熱阻；主軸機械振動使得軸承因受到附加的軸向力和徑向力，且隨著轉速的增大，振動加劇，軸承生熱增加。

4.2 空氣流量對軸承溫升的影響

在供油量0.4 mL/h，油運動黏度22 mm2/s，主軸轉速分別為4 000，8 000 r/min下，軸承溫升的仿真計算值和試驗值隨空氣流量的變化曲線如圖4所示。由圖可知，溫升計算值和試驗值間的誤差較小，且二者都隨空氣流量增大，散熱加強，溫升降低。

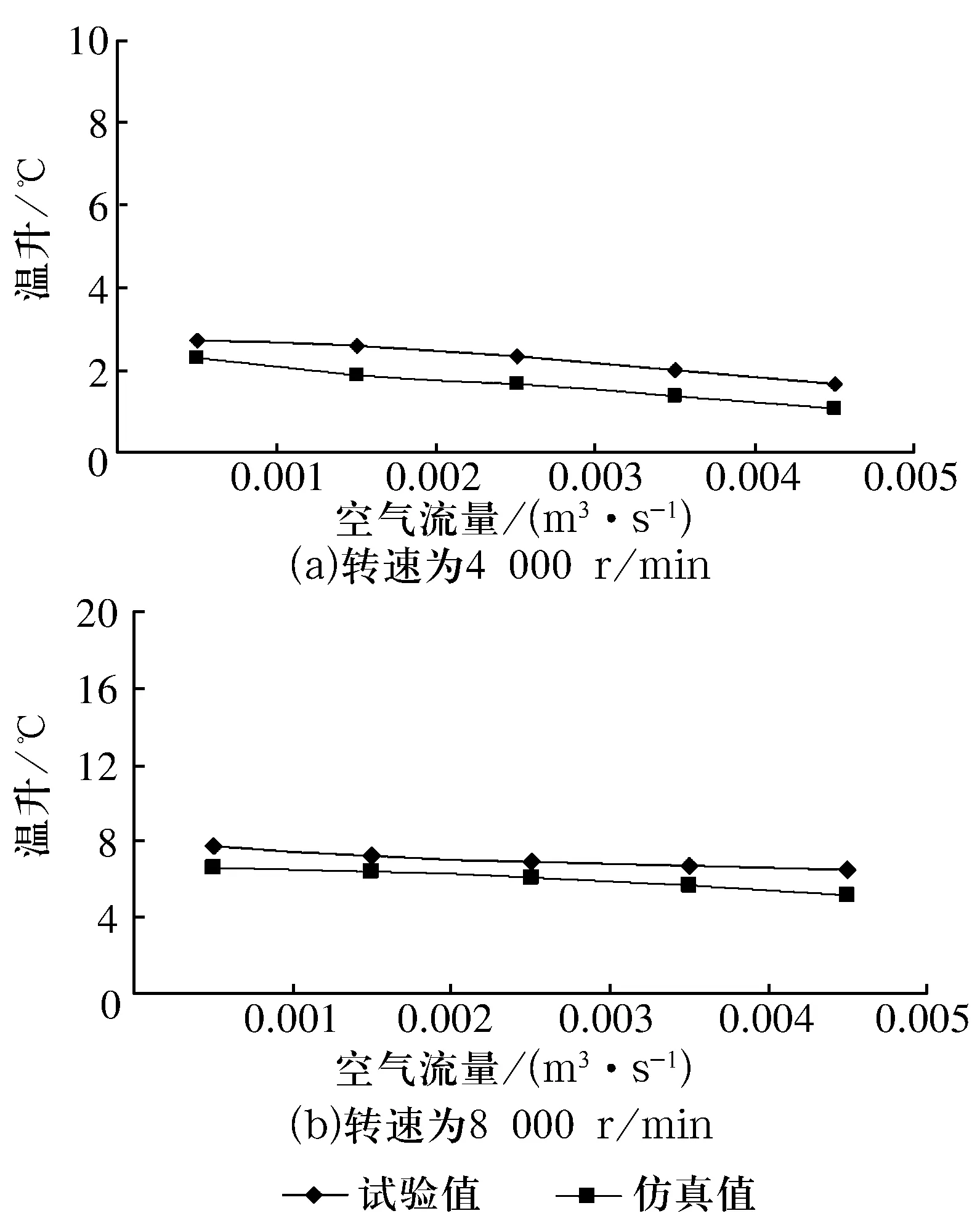
圖4 軸承溫升隨空氣流量的變化曲線Fig.4 Variation curve of temperature rise of bearing with air flow rate

4.3 供油量對軸承溫升的影響

在主軸轉速8 000 r/min，空氣流量2.5×10-3m3/s，油運動黏度22 mm2/s下，軸承溫升的計算仿真值和試驗值隨供油量的變化曲線如圖5所示。由圖可知，隨著供油量的增加，軸承溫升先減小后逐漸增大，當供油量為0.3 mL/h時，溫升最低，說明供油量存在一個最佳值。隨著供油量的增大，潤滑和對流換熱效果增強，溫升降低；當達到最佳值時，溫升最低；之后隨著供油量的進一步加大，球的繞流阻力損失快速增加，生熱增加，溫升增大。

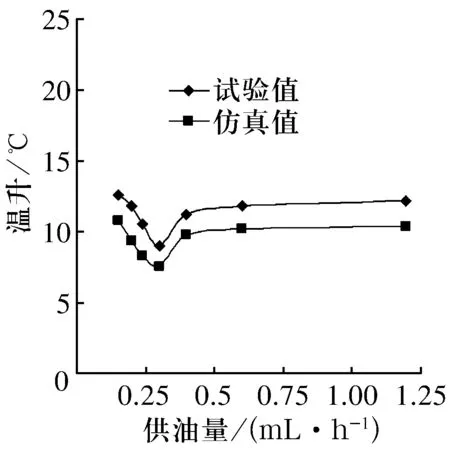
圖5 軸承溫升隨供油量的變化曲線Fig.5 Variation curve of temperature rise of bearing with supplied oil flow rate

5 結束語

基于熱網絡法，考慮高速主軸工作時結構約束、軸承的結構特性、冷卻/潤滑等氣/液特性對熱傳導、換熱和散熱特性的影響，研究了油氣條件下高速角接觸球軸承的溫升特性。對所建熱網格模型進行了仿真求解和試驗驗證，結果表明仿真結果和試驗值間的誤差較小，證明了所建模型的合理性。運用該模型可以更好地預測高速主軸角接觸球軸承的溫度場及變化，有利于準確掌握高速主軸的熱特性及變化規律，提高主軸工作精度和壽命，為高速主軸設計提供參考。