金屬材料彎曲成型的計算機模擬分析
陳 璇
(江西恒大聲學技術工程有限公司, 江西 南昌 330000)
1 金屬材料彎曲成型的計算機模擬分析方法設計
1) 引入本構方程,在金屬材料彎曲成型的計算機模擬分析中,應力與應變的關系是影響模擬結果的重要因素,建立金屬材料的彈塑性本構關系,首先要確定金屬材料成型前的應力特征;其次是金屬材料成型后塑性流動情況,金屬材料成型過程中,必須準確求出應力狀態與應變增量的關系式,為了使計算數值模擬更有效,適當減少計算的工作量作為必須考慮的問題之一。高溫狀態金屬材料成型的本構方程可以表示為:
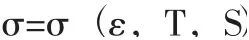
式中,ε 表示金屬材料應變速率;T 表示成型的溫度;S表示金屬材料內部組織參數。
2) 建立有限元幾何模型。確定了金屬材料的本構關系后,通過建立有限元幾何模型將金屬材料的截面圖載入到前處理器中,首先,對于厚度小于5mm 的金屬材料,在一定溫度下彎曲成型時,由于模具的上部采用弧形凸起結構,毛坯采用厚度均勻的弧形材料,因此在計算機模擬中,金屬材料彎曲可以作為軸對稱問題的一部分去解決。接著采用極坐標進行描述,金屬材料彎曲部分就可以根據實際產品的尺寸通過軸對稱件旋轉0 角而獲得,在成型過程中所用的模具視為剛體,不考慮變形因素。
3) 確定彎曲成型溫度,在金屬材料彎曲成型工藝中,溫度對彎曲成型的性能影響非常大。本文通過計算機對成型性能加以控制,依托金屬材料的本構關系,給配料以及模具進行高溫處理,很多研究者都將模具作為剛性體,不考慮金屬材料成型過程模具的形變,適當控制金屬材料的變形程度。
4) 實現金屬材料彎曲成型,金屬材料彎曲成型過程中,采用被普遍認可的非線性有限元軟件模擬了金屬材料的成型過程。引入的本構方程可以求出金屬材料的應力狀態與應變增量的關系,再根據建立的有限元幾何模型確定彎曲成型的溫度,有限元模擬過程流程圖如圖1 所示。
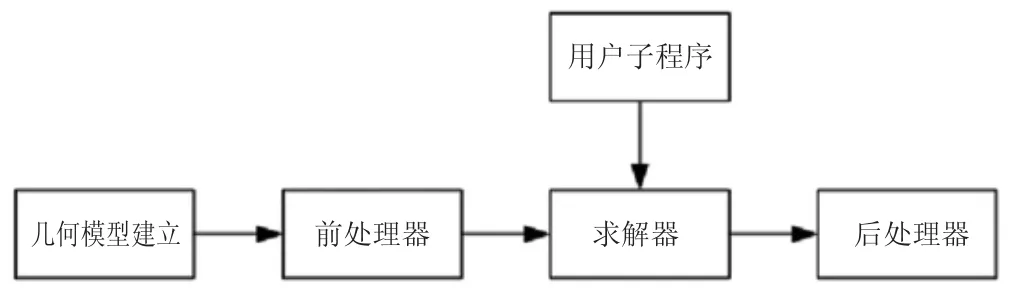
圖1 有限元模擬過程流程圖
基于本構方程的引入建立有限元幾何模型;依托金屬材料彎曲成型溫度的確定,實現金屬材料彎曲成型。完成提出的金屬材料彎曲成型的計算機模擬分析。
2 對比實驗
為了驗證本文金屬材料彎曲成型的計算機模擬分析方法能夠有效模擬金屬材料彎曲成型,基于金屬材料彎曲成型的計算機模擬分析方法,以及基本模擬分析方法,制作合金延伸率對比實驗。
1) 實驗材料。本實驗采用商業用的合金,其化學成分見表1,平均晶粒直徑大約在8μm,厚度為2.2mm,單向延伸率最大可超過300%。

表1 合金的化學成分(wt%)
2) 實驗方法。本文研究的合金溫度選擇100℃~600℃之間,應變速率在0.15s-1~0.006s-1 之間,采用基于金屬材料彎曲成型的計算機模擬分析方法,以及基本模擬分析方法對合金拉伸,拉伸過程通過計算機進行監控,合金夾頭的運動速度要隨時根據合金的拉伸長度調節,來保證合金的拉伸應變速率恒定,關系式如下:式中,v表示合金夾頭的運動速度,v表示合金的長度。在實驗溫度為100℃~600℃下,對合金進行應變速率恒定拉伸,應變速率對應的拉伸速度見表2。
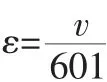
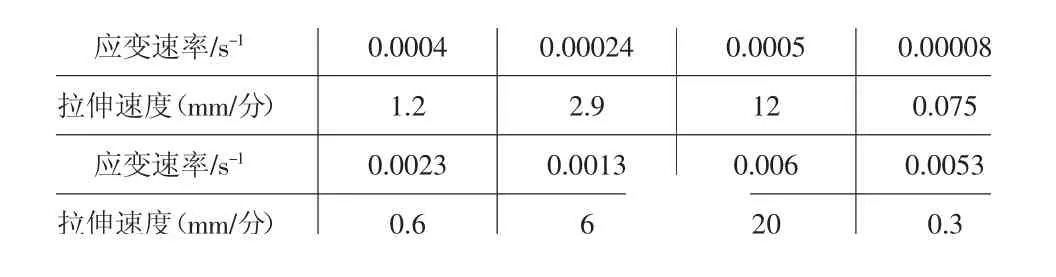
表2 應變速率對應的拉伸速度
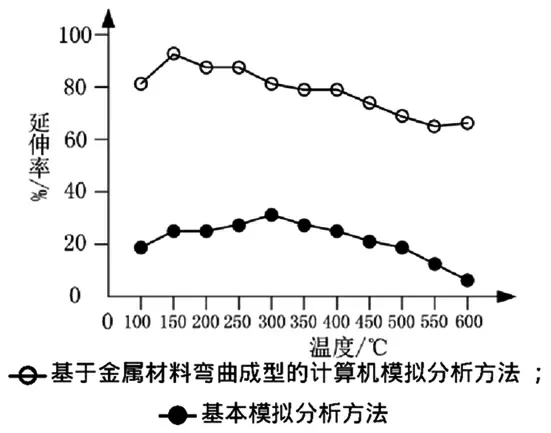
圖2 延伸率與溫度變化曲線
3) 數據處理與結果分析。實驗采集到的數據利用Origin5.8 軟件進行處理分析,得到延伸率與溫度變化曲線,如圖2。
根據實驗結果可知,采用基于金屬材料彎曲成型的計算機模擬分析方法,合金的延伸率最高可達93%,最低也可以達到65%,可以實現合金材料的彎曲成型,提高金屬材料的質量;同時與基本模擬分析方法相比,在保證拉伸速度一致的條件下,使用兩種方法的成型效果相差不大,都能實現彎曲成型,但是基于金屬材料彎曲成型的計算機模擬分析方法效果較好,能有效保證金屬材料的彎曲變形質量。
3 結語
本文提出了金屬材料彎曲成型的計算機模擬分析,在引入本構方程的基礎上建立有限元幾何模型,通過彎曲成型溫度的確定實現金屬材料彎曲成型,從而實現本文的模擬分析研究。

