等溫吸附量方程常數(shù)的物理含義及無(wú)因次吸附量方程

陳元千，劉浩洋，湯晨陽(yáng)，干 磊

（中國(guó)石油勘探開(kāi)發(fā)研究院，北京100083）

LANGMUIR（蘭格苗爾）于1918年發(fā)表了著名的蘭氏等溫累積吸附量方程［1］，受到世人的重視和廣泛應(yīng)用。但應(yīng)當(dāng)指出，蘭氏方程是一個(gè)具有兩個(gè)常數(shù)的非線性經(jīng)驗(yàn)方程。蘭氏曾指出，方程的常數(shù)a和b是兩個(gè)與氣體物理性質(zhì)和溫度有關(guān)的常數(shù)。但他并不清楚a和b的實(shí)際物理含義。陳元千等于2018年發(fā)表了等溫吸附量方程和解吸量方程的推導(dǎo)結(jié)果［2］。同時(shí)，對(duì)蘭氏方程進(jìn)行了完整的理論推導(dǎo)，得到了蘭氏的等溫瞬壓吸附量方程和瞬壓解吸量方程。陳氏方程和蘭氏方程都具有兩個(gè)方程常數(shù)，通過(guò)推導(dǎo)，明確了方程常數(shù)的物理含義，并建立了具有廣泛理論意義的無(wú)因次吸附方程。陳氏方程的常數(shù)A和蘭氏方程的常數(shù)a都表示樣品的極限累積吸附量；陳氏方程的常數(shù)B和蘭氏方程的常數(shù)b都表示等溫瞬壓吸附量遞減率；陳氏方程的AB和蘭氏方程的ab都表示樣品的最大初始理論吸附量。

1 等溫吸附量方程常數(shù)的物理含義

當(dāng)以表壓表示壓力時(shí)，陳元千等提出的等溫累積吸附量方程和等溫瞬壓吸附量方程［2］分別為：

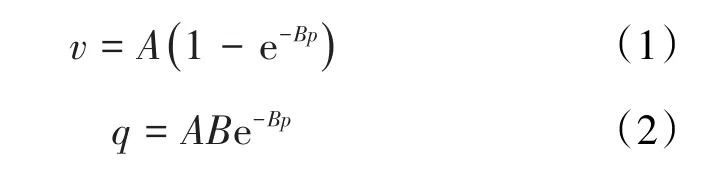
當(dāng)p→∞時(shí)，由（1）式得陳氏方程的等溫極限累積吸附量為：

由（3）式看出，等溫極限累積吸附量等于常數(shù)A。由文獻(xiàn)［2］知，（1）式和（2）式中的B為等溫瞬壓吸附量遞減率。

將（3）式代入（1）式得：

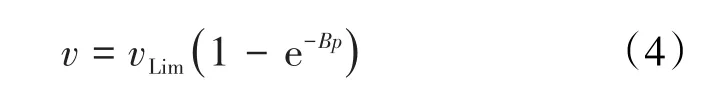
由（4）式對(duì)壓力求導(dǎo)得陳氏的等溫瞬壓吸附量方程為：

當(dāng)p=0時(shí)，由（5）式得p=0時(shí)的最大初始理論吸附量為：

再將（3）式代入（6）式，得陳氏的最大初始理論吸附量為：