某鐵路站房大跨屋蓋鋼結構設計與分析
殷 靜
(中鐵第四勘察設計院集團有限公司 湖北武漢 430063)
1 引言
目前公共建筑為實現大跨空間,普遍采用下部混凝土結構與上部鋼屋蓋結構的組合形式,鐵路旅客站房就屬于這類典型的公共建筑。在對站房施工圖進行審核的過程中發現很多設計院在設計時常常各自分開計算,即下部主體結構設計時,將上部鋼屋蓋等效成鋼梁或樓板計算,并未真實考慮鋼屋蓋對下部結構的剛度貢獻;進行上部鋼屋蓋設計時,常常也未考慮下部結構對上部屋蓋的邊界影響[1-2]。為此,本文選取鐵路站房中比較常見的站型及規模,在施工圖審核過程中通過單體鋼屋蓋模型和整體模型的對比,分析兩種模型的受力特性,研究大跨鋼屋蓋與其下部混凝土結構的協同工作特性及抗震薄弱環節,從而驗證結構體系選型的合理性及結構安全性,為今后類似工程施工圖審核提供參考[3]。
2 工程概況
某鐵路站房南候車廳建筑平面尺寸約為139 m×48 m,建筑高度約28.4 m。結構地上四層,一、二層層高為4.8 m;地下二層,地下一層為地鐵集散廳,層高5 m,局部地下二層為地鐵換乘層。下部結構柱網尺寸8.1 m、15.6 m和24 m,屋蓋縱橫向最大跨度36 m,建筑剖面圖見圖1。
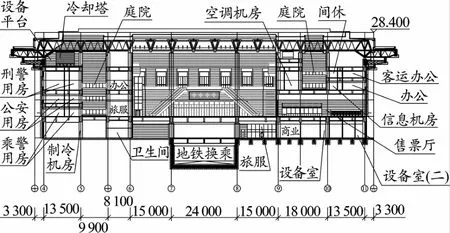
圖1 鐵路站房剖面(單位:mm)
該建筑設計使用年限為50年,安全等級為一級,結構重要性系數1.1。
2.1 設計荷載
(1)恒荷載
①結構自重:放大1.1倍考慮節點重量;②屋蓋上弦荷載:金屬屋面0.65 kN/m2;玻璃屋面1.0 kN/m2;③屋蓋下弦荷載:吊頂及吊掛0.35 kN/m2,馬道1.0 kN/m2;設備管道荷載根據實際布置按線荷載施加。
(2)活荷載 0.5 kN/m2;馬道檢修活荷載 1 kN作用在跨中驗算。
(3)風荷載
根據《建筑結構荷載規范》(GB 50009-2012)[4](下文簡稱荷載規范),基本風壓按百年一遇取值為0.45 kN/m2,地面粗糙度類別為A類。
(4)雪荷載
基本雪壓按照100年重現期取0.5 kN/m2,同時考慮雪荷載不均勻分布以及半跨均布的情況。
(5)溫度荷載
根據當地氣候特征資料,同時參考荷載規范[4],控制鋼結構合龍溫度在10~15℃,取升溫+30℃、降溫-30℃進行溫度工況的施加。
(6)地震作用
根據《建筑抗震設計規范》(GB 50011-2010)[5],工程抗震設防烈度為7度(0.1 g),抗震設防類別為乙類;設計地震分組為第二組,場地類別為II類。
2.2 設計荷載組合
工程設計荷載組合見表1。表中各個荷載工況的分項系數和組合值系數按照荷載規范取值,由于該工程屬于大跨度空間結構,因此適當考慮了豎向地震作用組合。
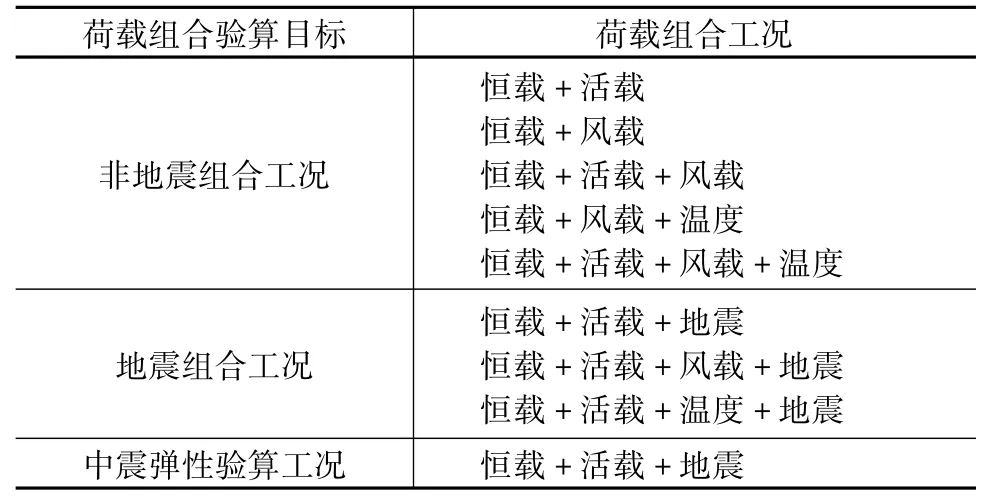
表1 荷載組合
3 屋蓋結構體系
該鐵路站房屋蓋采用正交正放管桁架結構體系,根據建筑效果及支承條件,將桁架分為立體桁架和平面桁架兩種[6]。其中,作為主受力桁架,立體桁架沿雙向交錯布置。懸挑部分采用平面桁架,共37榀,最大懸挑長度約14 m,平面懸挑桁架間通過支撐連接形成整體。屋蓋立體桁架桿件及平面桁架腹桿采用無縫圓鋼管,平面桁架弦桿采用矩形鋼管,材質為Q345B。節點采用相貫節點和焊接球節點。圖2為屋蓋桁架軸測圖。
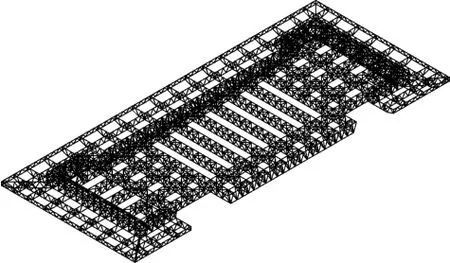
圖2 屋蓋桁架軸測圖
立體桁架為倒三角形桁架,桁架下弦采用φ325×20,中間大廳由于建筑采光要求,采用單向立體三角桁架,桁架邊部設置支撐和系桿,保證其空間穩定性。根據建筑造型的要求,高低變化處通過設置局部雙層桁架來實現(見圖3~圖5)。
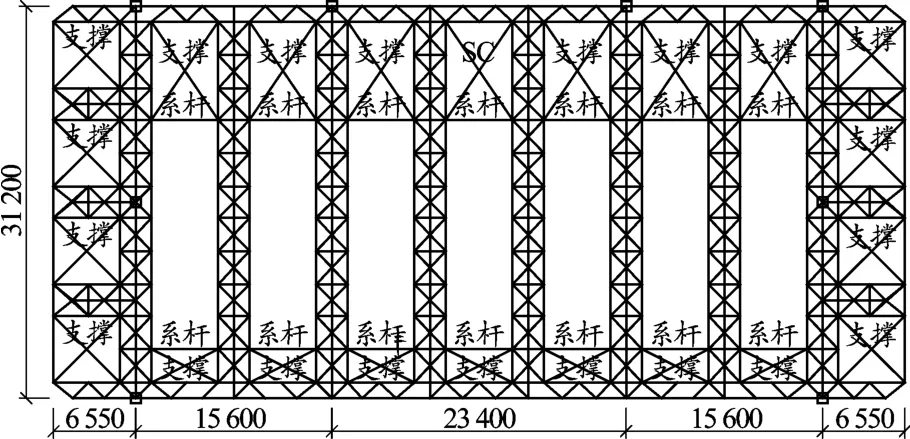
圖3 中間采光大廳屋蓋結構布置(單位:mm)

圖4 局部雙層桁架示意(單位:mm)

圖5 立體、平面桁架轉換示意
4 設計思路
4.1 上部鋼屋蓋結構設計
對于上部鋼屋蓋結構,設計過程中常用的邊界約束條件有靜定約束和全三向鉸接兩種。采用靜定約束邊界條件時結構跨中位移偏大,桿件內力小;而采用全三向鉸接約束邊界條件時結構跨度位移小,桿件內力大(尤其是支座附近)。
本工程采用靜定約束和全三向鉸接兩種不同的邊界條件進行包絡設計,通過取兩種模型的包絡位移和內力,驗算屋蓋結構位移、桿件應力比等指標是否滿足要求。
4.2 總裝結構設計
通過建立下部結構的總裝模型,對鋼屋蓋進行驗算,對考慮下部結構實際剛度后的結構受力特性進行分析,并對屋蓋結構桿件再次進行包絡設計[7]。
采用Midas Gen軟件分別建立鋼屋蓋單體模型和整體模型,其中單體模型為考慮不同邊界約束包絡設計后的靜定約束模型。Midas Gen中桁架弦桿采用梁單元,桁架腹桿采用桁架單元。鋼屋蓋單體模型和整體模型見圖6~圖7。
圖6 鋼屋蓋單體模型
圖7 總裝模型
5 上部鋼屋蓋結構
5.1 單體鋼結構屋蓋結果分析
(1)撓度
1.0恒載+1.0活載下,桁架結構中心區域豎向撓度最大,最大撓度值為111 mm,撓跨比為1/324(跨度36 m);周邊懸挑端撓度值為33 mm,撓跨比為 1/333(懸挑 11 m),見圖 8,均滿足規范[8-9]規定的撓度限制要求。要求施工單位在施工過程中對撓度較大處采取適當的起拱措施。
(2)桿件應力比
①非地震組合和多遇地震組合工況驗算
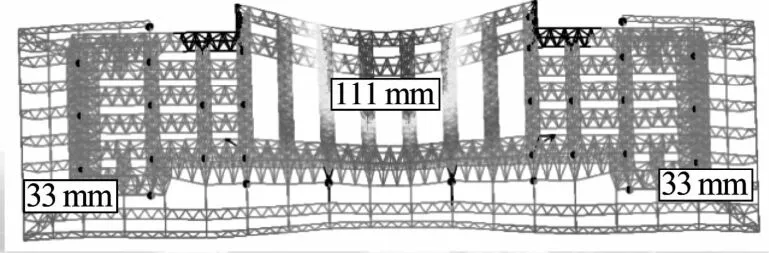
圖8 標準組合下撓度值
非地震組合和多遇地震組合工況下,考慮壓桿穩定系數,桿件應力比基本控制在0.85以下,個別桿件應力比達到0.9(支座處),滿足設計控制指標。桿件驗算應力比統計圖及桿件應力比分布圖見圖9、圖 10。

圖9 桿件應力比統計
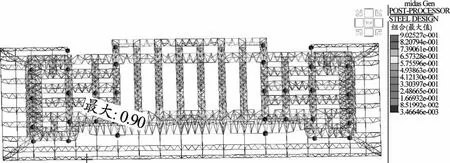
圖10 桿件應力比分布圖
②中震彈性驗算
支座附近桿件為屋蓋結構的關鍵構件,設計過程中對其采用中震彈性驗算,并考慮壓桿穩定系數。取消地震內力調整后,桿件應力比最大值為0.9,滿足中震彈性的控制指標。
5.2 總裝模型分析
(1)撓度及應力比
采用midas Gen對屋蓋單體模型和總裝模型進行對比分析,得到兩種模型在同樣荷載條件下的撓度值和桿件最大應力比,見表2。
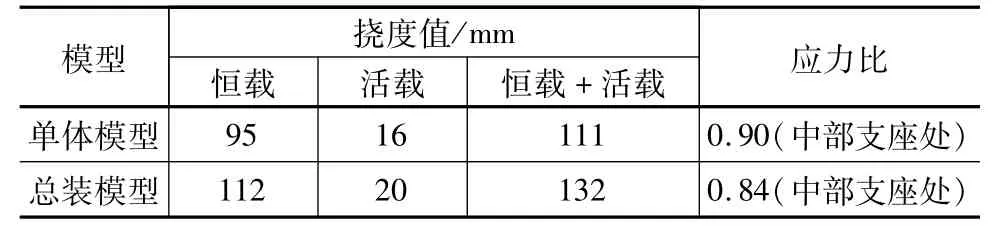
表2 兩種模型結果對比
由表2可知,單體模型由于假定下部結構為無限剛體,采用三向鉸接計算;而總裝模型考慮了下部結構的實際剛度,因此單體模型的撓度值比總裝模型小,但由于單體模型支座約束較強,應力比會比總裝模型偏大。對于結構構件設計,采用兩種邊界約束條件包絡設計后的單體模型是偏于安全的,與總裝模型計算結果接近。
(2)周期
結構前三階振型和周期見圖11。第1階振型為X向平動,周期為1.180 s;第2階振型為Y向平動,周期為0.988 s;第3階振型為扭轉,周期為0.947 s。周期比為0.802,滿足規范要求。
由圖11可以看出兩種模型屋蓋部分振型形式基本一致,但整體模型中除豎向振型之外還夾雜較多的平動振型,這與下部混凝土部分參與振動有關。
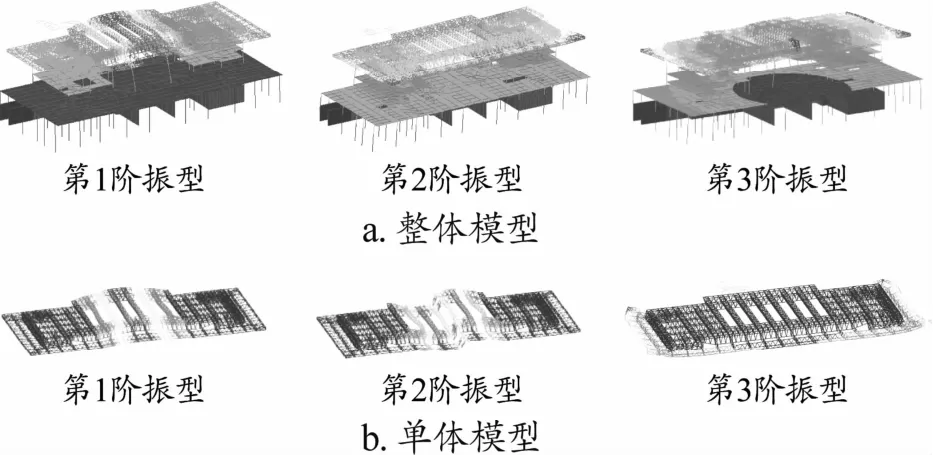
圖11 結構前三階振型
(3)下部結構總裝分析與單體分析對比
采用midas Gen進行分析后,提取總裝模型和下部單體模型的結構關鍵參數結果進行對比,具體見表3。
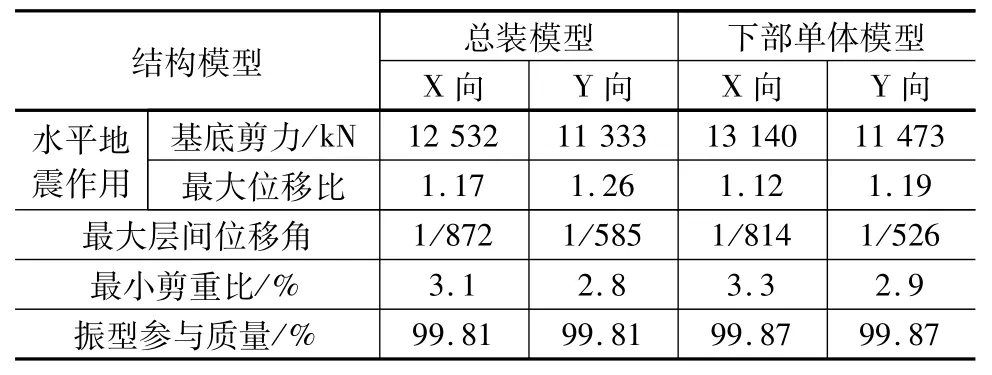
表3 關鍵參數結果對比
由表3可知,總裝模型的基底剪力略小于單體模型,但相差不大;總裝模型位移比偏大,這可能是由于上部鋼屋蓋鞭梢作用的原因[10],對于與鋼屋蓋相連的混凝土框架柱的內力有放大作用,設計時應適當加大該框架柱配筋。
6 支座節點構造設計
支座節點不僅能阻止結構發生剛體位移,增強結構的整體性能,同時可有效抵消結構支座的部分反力[11-12]。該站房鋼屋蓋支座在設計時考慮如下因素:
(1)支座節點構造需滿足計算假定;
(2)支座節點各部位尺寸應避免與其他構件碰撞,且保證足夠凈距以保證結構的控制變形;
(3)保證鋼屋蓋在地震作用下的安全性,尤其是支座處的安全可靠性。
本工程選用抗震球形支座,構造如圖12所示。通過提取模型中的支座受力,確定支座產品參數。
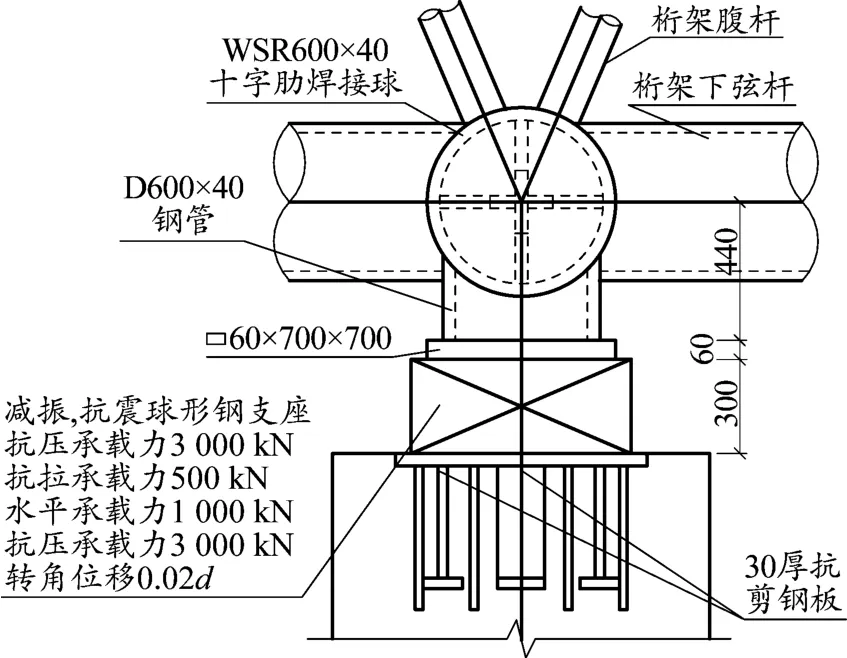
圖12 支座節點構造(單位:mm)
7 結論
(1)針對某鐵路站房大跨度鋼結構屋蓋的設計思路和流程進行了詳細介紹,根據建筑自身造型要求選用了合理的結構體系。
(2)單體鋼屋蓋結構應采用靜定約束邊界條件和全三向鉸接邊界條件進行包絡設計。
(3)總裝模型結果對比分析表明:采用兩種邊界約束條件包絡設計后的單體模型進行設計偏于安全,與總裝模型計算結果比較接近。
(4)對于下部混凝土結構,考慮上部鋼屋蓋的鞭梢作用后,與其相連的下部混凝土框架柱受力有所增加,該框架柱配筋建議適當放大。
(5)該鐵路站房結構的控制指標嚴格按照相關規范制定,各項設計結果均滿足規范要求,可為今后類似工程提供參考。

