QAM解調(diào)及頻偏估計聯(lián)合算法

趙瑩琦 楊 萃

1(廣州大學松田學院 廣東 廣州 511370)2(華南理工大學電子與信息學院 廣東 廣州 510640)

0 引 言

正交幅度調(diào)制技術(Quadrature amplitude modulation, QAM)既調(diào)幅又調(diào)相，頻譜利用率高，在頻譜資源日益緊張的現(xiàn)代數(shù)字通信中顯得尤為重要，廣泛地應用于數(shù)字電視傳輸系統(tǒng)和數(shù)字MMDS系統(tǒng)[1-2]。QAM技術雖然頻譜利用率高而備受關注，然而其解調(diào)時需要做精確的信道估計以達到載波同步才能實現(xiàn)正確解調(diào)[3-4]。

多普勒頻偏體的運動速度與發(fā)送信號頻率的相對關系有關。在電磁波傳播環(huán)境下，由于電磁波傳播速度高達3×108m/s，即使物體處于高速運動時，產(chǎn)生的載波偏移仍然很小，很多時候可以忽略。而在水下環(huán)境，由于電磁波衰減很快，因而只能通過聲音信號作為傳輸載體，而聲速只有每秒幾百米，因而在水下多普勒頻移使得載波在接收端產(chǎn)生很大的載波偏移，造成較大的誤碼率。另外在水下環(huán)境，水深和水質(zhì)均會對聲速造成影響，從而水下環(huán)境多普勒頻偏較不穩(wěn)定。這樣一來，要能克服多普勒頻偏就要求接收端能實時地跟蹤信道的情況、及時得到載波偏移的信息[5-7]。

相干解調(diào)需要通過本地鎖相環(huán)恢復載波，并保持相位鎖定，需要進行信道估計。QAM自適應解調(diào)算法解調(diào)性能優(yōu)良，但是需要較長時間算法才能收斂，因而不適于實時解調(diào)。信息處理領域涌現(xiàn)出了一批QAM自適應解調(diào)算法[8-13]，如文獻[9]利用動態(tài)特性克服多徑效應，實現(xiàn)自適應解調(diào)；文獻[11] 利用最小均方(LMS)算法實現(xiàn)解調(diào)，降低了采樣率和數(shù)據(jù)處理的速度；文獻[12]提出將無率碼與解調(diào)算法結合，實現(xiàn)高階QAM解調(diào)。利用前期QAM解調(diào)理論研究的成果，一些學者將其運用到載波頻偏估計中，如：何維等[14]提出了一種基于加權相位直方圖的QAM載波頻偏估計算法，該算法無需星座圖及前導信息等輔助條件，但高質(zhì)量的估計性能僅局限于高信噪比的條件下；李炎新等[15]提出的自適應濾波解調(diào)算法既能夠完成解調(diào)又能估計出載波頻偏，其解調(diào)的誤碼率在理論上與相干解調(diào)法一致，但是其載波頻偏估計方法受噪聲影響大。雖然可以用低通濾波器濾波去噪，但是當信噪比較低時，算法的性能仍然不理想。

相干解調(diào)和自適應解調(diào)算法都是直接通過碼元樣點來解調(diào)，也就是在時域上進行解調(diào)[16]。本文通過將碼元樣點變換到頻域[17]，利用頻域最小二乘逼近(Least Square Approximation，LSA)思想，在解調(diào)的同時求解載波偏移。由于在碼元樣點的頻域上，載波信號能量集中而白噪聲均勻分散地分布，因而該解調(diào)算法受噪聲影響小，誤碼率低。通過該算法對接收到的信號進行頻率估計可以估計出載波偏移，對接收信號進行幅度和相位的估計可以實現(xiàn)QAM解調(diào)。

1 QAM解調(diào)及頻偏估計聯(lián)合算法

QAM是兩路獨立的基帶信號對兩個相互正交的同頻載波進行抑制載波雙邊帶調(diào)幅信號。同步采樣信號為：

d(n)=Accos(ωcn+φc)-Assin(ωcn+φc)+z(n)

(1)

式中：z(n)為加性高斯白噪聲，Accos(ωcn+φc)-Assin(ωcn+φc)為QAM調(diào)制信號。ωc為載波頻率，φc為載波相位偏移。解調(diào)時可以將本地產(chǎn)生的兩個與載波同頻同相的分量作為參考輸入，然后通過相關或者自適應迭代來得到Ac和As來實現(xiàn)解調(diào)(相干解調(diào)，自適應解調(diào))。式(1)所描述的信號可以寫為：

d(n)=Acos(ωcn+φc+φ0)+z(n)

(2)

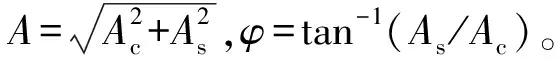
(3)

沒有噪聲時標準正弦信號的DFT譜在正負頻率處有兩個譜峰，其表達式為：

(4)

我們只考慮正頻率處的譜峰，其能量譜為：

(5)

假設能量譜上正頻率處的譜峰位于k0譜線處，那么載波頻率可以寫為：

(6)

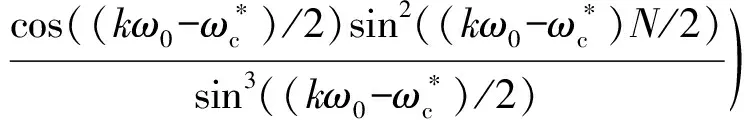
(7)

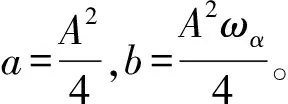
(8)

由于正弦信號是窄帶信號，其能量高度集中在譜峰附近的主瓣范圍內(nèi)，因而只需要在主瓣范圍內(nèi)使得樣點的能量譜逼近標準正弦信號的能量譜，即：

(9)

根據(jù)最小二乘原則，求解可得：

式中：

y=[Y0(-q),…，Y0(0),…，Y0(q)]T

p=[P(k0-q),…，P(k0),…,P(k0+q)]T

式中：

從而不難求解：

式中：wu和wv是能量譜加權系數(shù)，表達式為：

因而有載波頻率估計值為：

根據(jù)式(3)，我們可以得到標準正弦信號相位的表達式為：

然而，僅用一個頻點來計算相位容易受到噪聲的干擾，使得估計結果不準確，因而采用窄帶內(nèi)多個頻點計算相位求平均值，可以得到：

(10)

(11)

(12)

2 仿 真

由于我們設計的算法是通過估計接收信號的頻率來實現(xiàn)載波恢復，通過估計接收信號的幅度和相位來實現(xiàn)解調(diào)，因而首先通過仿真確定頻率、幅度和相位估計的結果與算法中補零倍數(shù)q的選擇之間的關系。

我們將q置為2、4，分別得到頻率、幅度和相位估計的均方誤差結果，將結果與各自的理論界(Cramer Rao Bound，CRB)[18]進行比較。

設置幅度A=100，相位φ0=0，頻率為ω∈[0,π]中的隨機值，進行10 000次蒙特卡羅仿真得到頻率估計的結果如圖1所示。

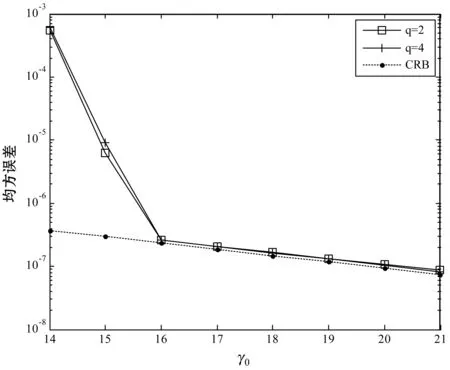
圖1 補零倍數(shù)對頻率均方誤差的影響

設置幅度隨機產(chǎn)生于A∈[50,100]，相位φ0=0，頻率為ω∈[0,0.2π]，得到幅度估計的結果如圖2所示。

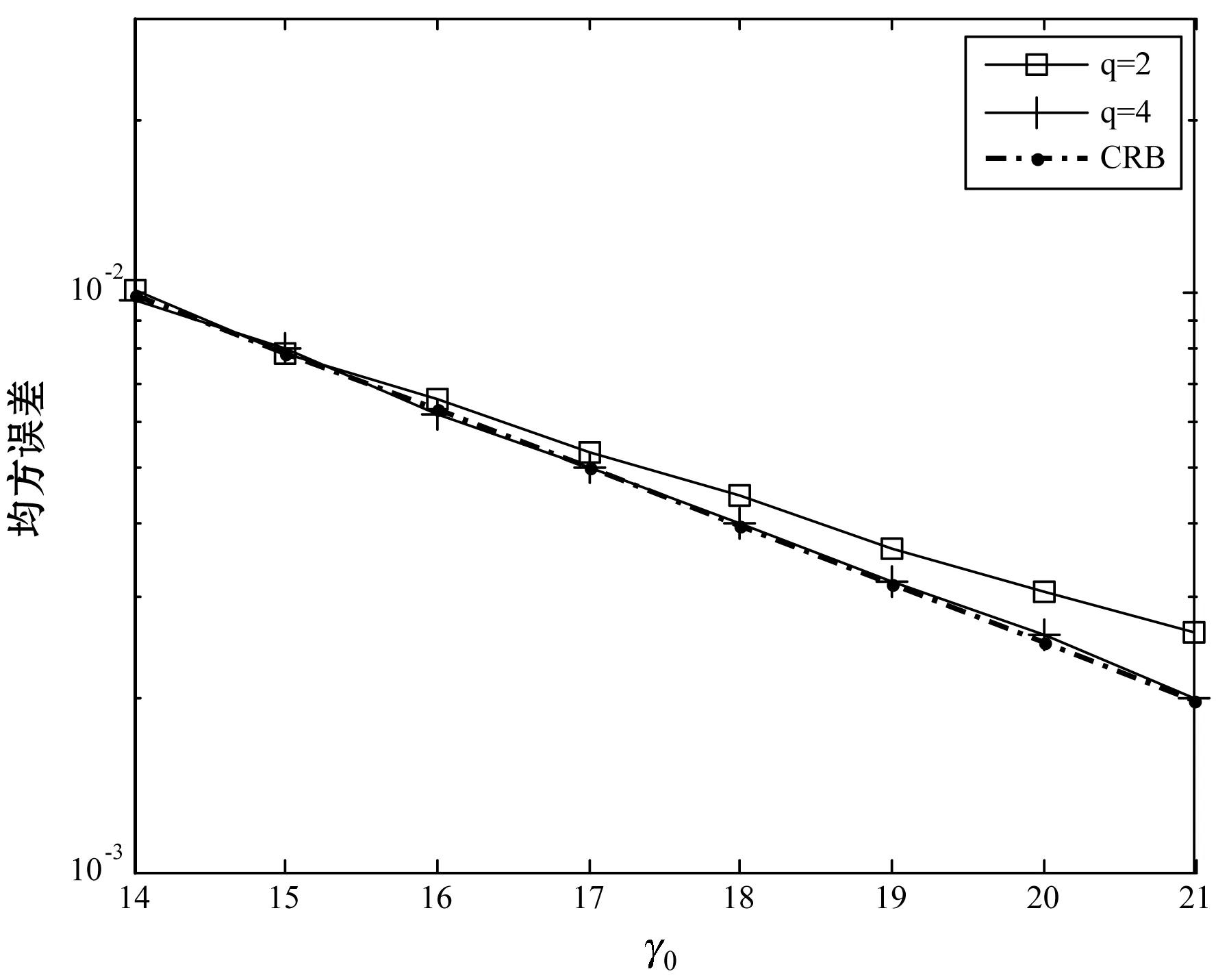
圖2 補零倍數(shù)對幅度均方誤差的影響

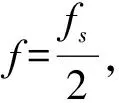
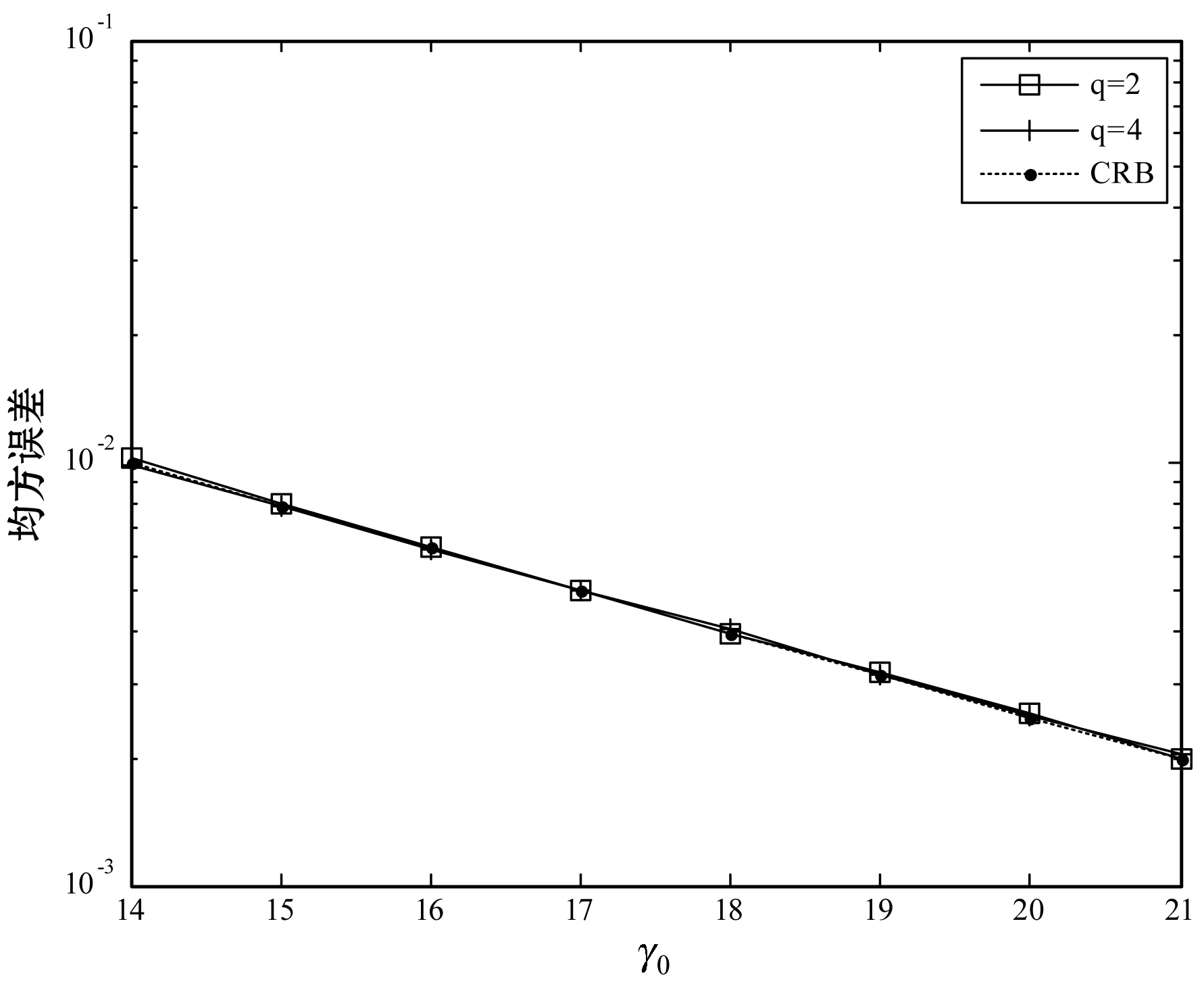
圖3 補零倍數(shù)對頻率均方誤差的影響

設置幅度隨機產(chǎn)生于A∈[50,100]，相位φ0=0.25π，頻率為ω∈[0,π]，得到相位估計的結果如圖4所示。

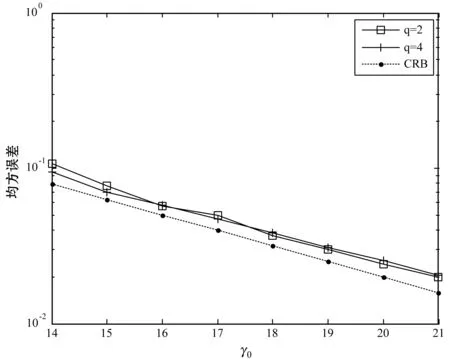
圖4 補零倍數(shù)對相位均方誤差的影響

設置幅度隨機產(chǎn)生于A∈[50,100]，相位φ0∈[0,0.8π]，頻率為ω=0.25π，得到相位估計的結果如圖5所示。

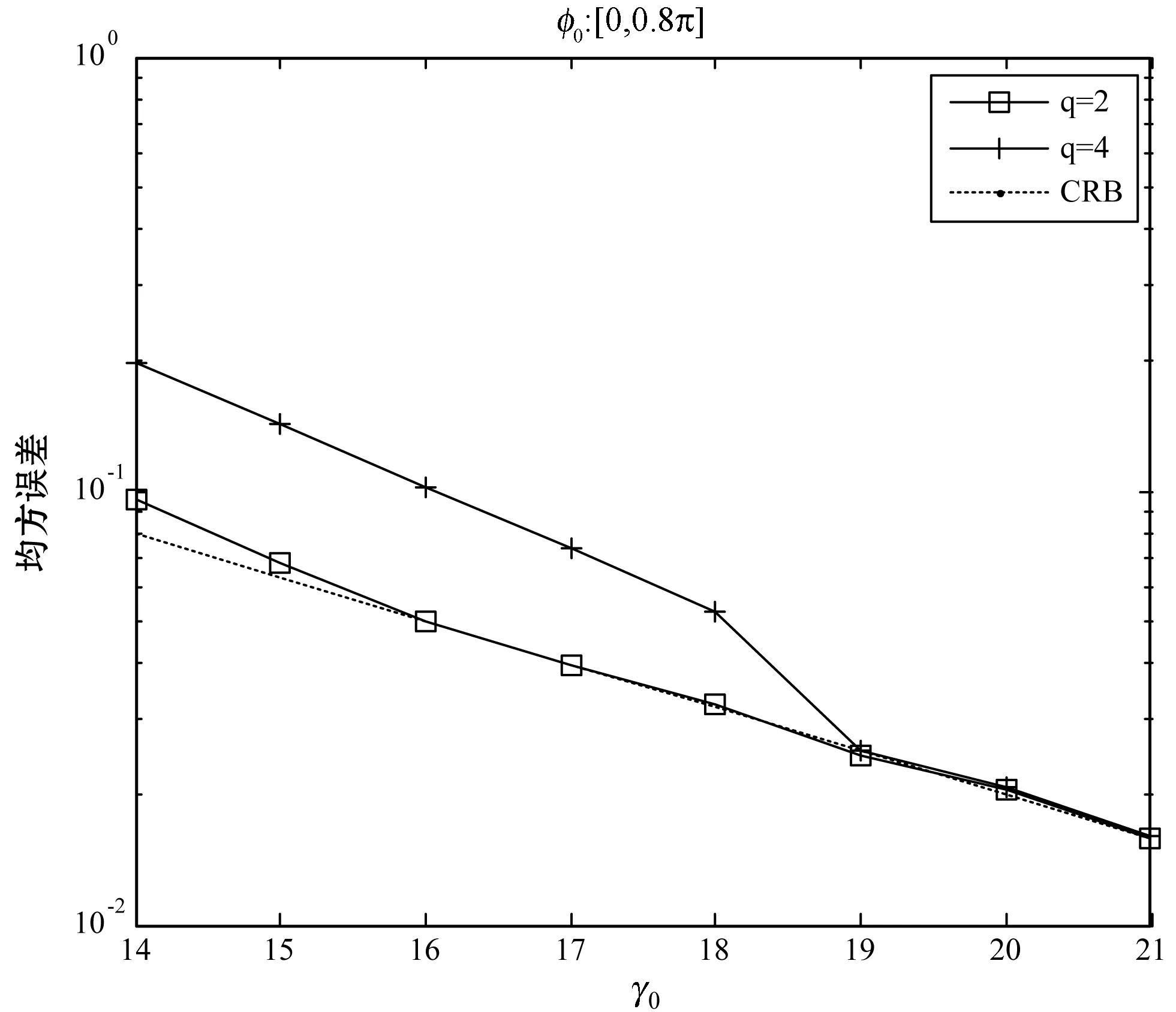
圖5 補零倍數(shù)對相位均方誤差的影響

設置幅度隨機產(chǎn)生于A∈[50,100]，相位φ0∈[0,0.5π]，頻率為ω=0.25π，得到相位估計的結果如圖6所示。

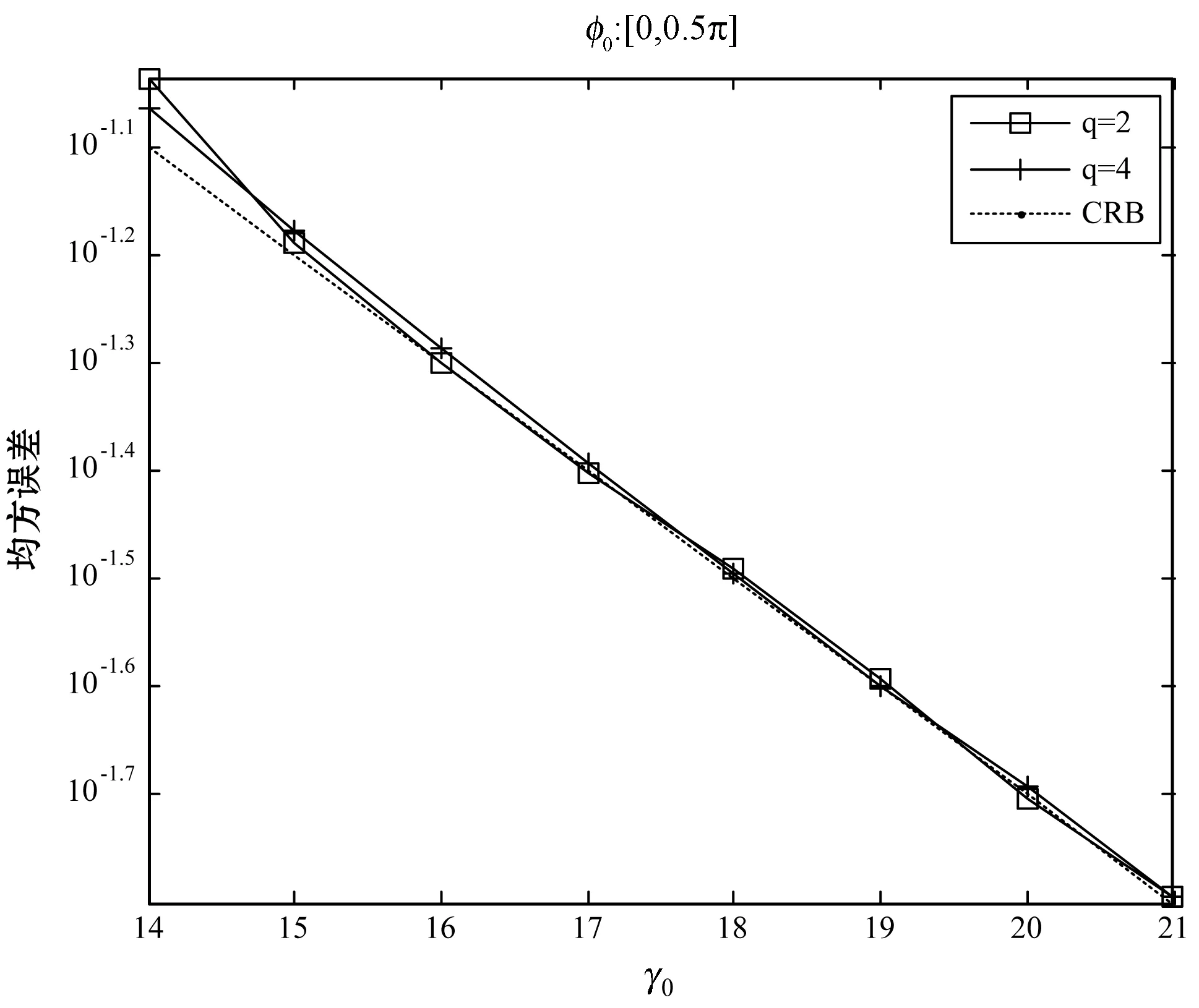
圖6 補零倍數(shù)對相位均方誤差的影響

取M=16，載波頻率fc=10 kHz，載波頻偏為Δfc=50 Hz，采樣頻率為fs=50 kHz，碼元長度為Tsym=1 ms。自適應迭代算法在一個碼元內(nèi)需要進行30～50次迭代才能實現(xiàn)解調(diào)[15]，計算量較大，因此本文對提出的算法與相干解調(diào)法這一類不需要迭代的算法進行對比，得到誤碼率的比較如圖7所示。

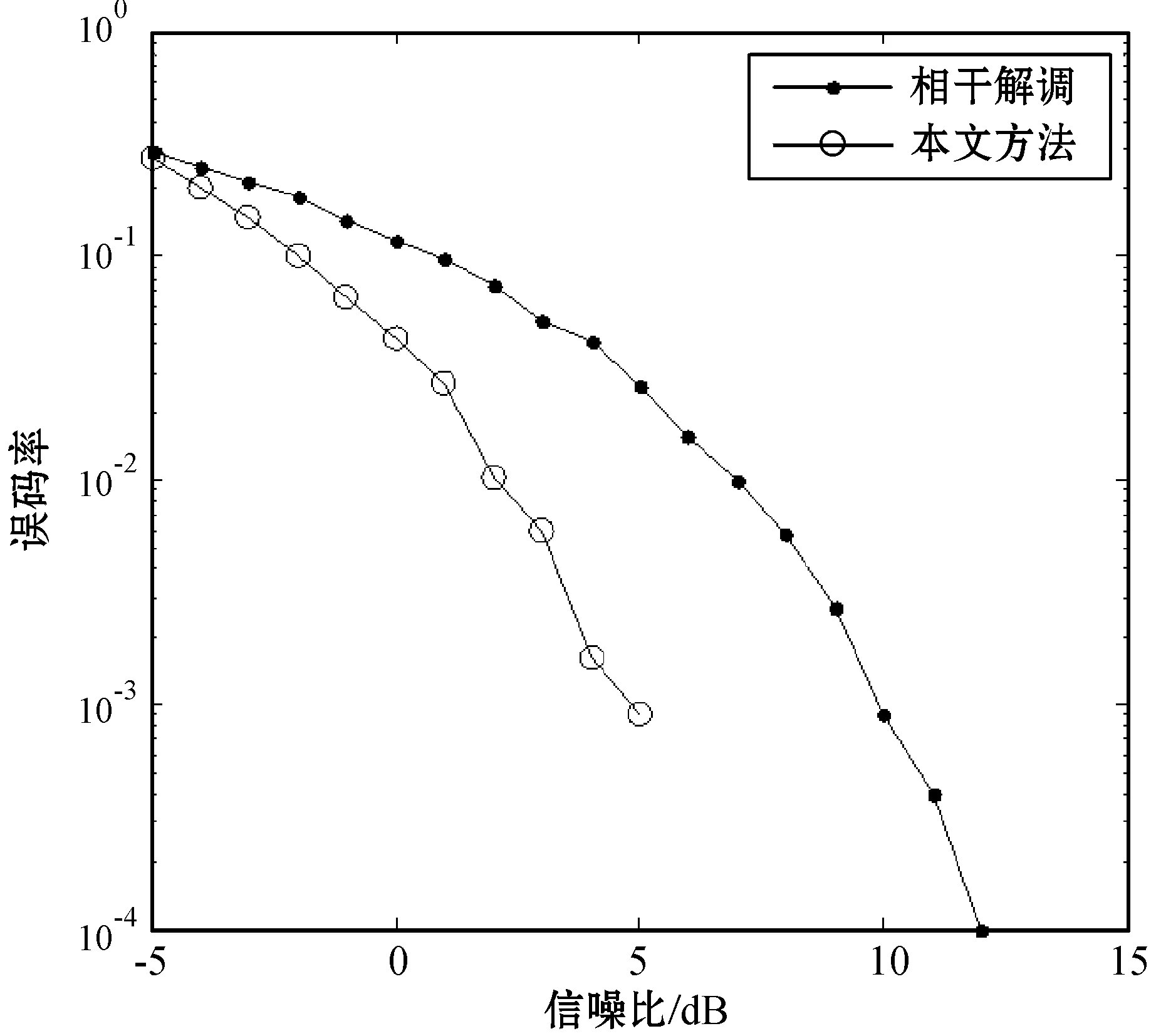
圖7 本文方法和相干解調(diào)的比較

3 結 語

本文提出了將QAM解調(diào)和載波頻率偏移估計相聯(lián)合的算法。在頻域中通過最小二乘逼近的方法，實現(xiàn)了載波頻偏估計。通過仿真，驗證了無論是頻率估計、幅度估計還是相位估計的均方誤差均達到CRB界。此外，與相干解調(diào)相比，聯(lián)合算法降低了QAM調(diào)制解調(diào)算法的誤碼率。